1. 图形学的依赖学科
- 基础数学
- 线性代数,微积分,统计…
- 基础物理
- 光学,力学…
- 其他
- 信号处理,数值分析…
- 以及一些审美
2. 向量
向量的定义,标准化,求和,坐标表示,求长度等知识
(图形学上默认以列向量表示)
2.1 点乘
2.1.1 定义和运算律
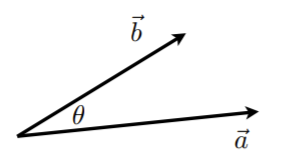
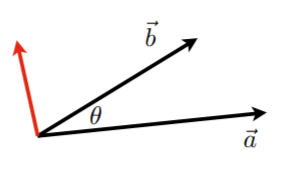
a⃗⋅b⃗=∥a⃗∥∥b⃗∥cosθcosθ=a⃗⋅b⃗∥a⃗∥∥b⃗∥ \begin{aligned} \vec{a} \cdot \vec{b} &= \Vert{\vec{a}}\Vert \Vert{\vec{b}}\Vert \cos{\theta} \\[2ex] \cos{\theta} &= \cfrac{\vec{a} \cdot \vec{b}}{\Vert{\vec{a}}\Vert \Vert{\vec{b}}\Vert} \end{aligned} a⋅bcosθ=∥a∥∥b∥cosθ=∥a∥∥b∥a⋅b
- 对于单位向量
cosθ=a^⋅b^ \cos{\theta} = \hat{a} \cdot \hat{b} cosθ=a^⋅b^
2.1.2 坐标的运算以及作用
找夹角和找投影
-
2D
a⃗⋅b⃗=(xaya)⋅(xbyb)=xaxb+yayb \vec{a} \cdot \vec{b} = \begin{pmatrix} x_a \\ y_a \end{pmatrix} \cdot \begin{pmatrix} x_b \\ y_b \end{pmatrix} = x_a x_b + y_a y_b a⋅b=(xaya)⋅(xbyb)=xaxb+yayb -
3D
a⃗⋅b⃗=(xayaza)⋅(xbybzb)=xaxb+yayb+zazb \vec{a} \cdot \vec{b} = \begin{pmatrix} x_a \\ y_a \\ z_a \end{pmatrix} \cdot \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = x_a x_b + y_a y_b + z_a z_b a⋅b=⎝⎛xayaza⎠⎞⋅⎝⎛xbybzb⎠⎞=xaxb+yayb+zazb
2.1.3 点乘的作用
- 两个向量之间的接近程度
- 分解向量
- 根据点乘结果正负判断前后
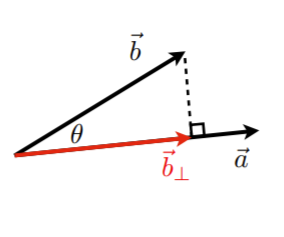
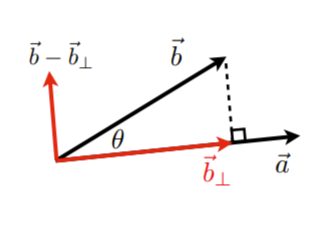
- b⃗⊥\vec{b}_\perpb⊥ :b⃗\vec{b}b 在 a⃗\vec{a}a 上的投影
- b⃗⊥\vec{b}_\perpb⊥ 必须沿着 a⃗\vec{a}a (或者沿着 a^\hat{a}a^ )
- 对应的模 kkk
- k=∥b⃗⊥∥=∥b^∥cosθk = \Vert{\vec{b}_\perp}\Vert = \Vert{\hat{b}}\Vert \cos{\theta}k=∥b⊥∥=∥b^∥cosθ
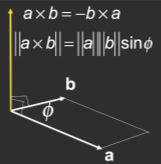
2.2 叉乘
- 叉乘的定义和运算律
- 右手定则判断叉乘方向
- 这节课都是右手坐标系,OpenGL是左手坐标系
2.2.1 叉乘的坐标计算
x⃗×y⃗=+z⃗y⃗×x⃗=−z⃗y⃗×z⃗=+x⃗z⃗×y⃗=−x⃗z⃗×x⃗=+y⃗x⃗×z⃗=−y⃗ \begin{aligned} \vec{x} \times \vec{y} &= + \vec{z} \\ \vec{y} \times \vec{x} &= - \vec{z} \\[1.25ex] \vec{y} \times \vec{z} &= + \vec{x} \\ \vec{z} \times \vec{y} &= - \vec{x} \\[1.25ex] \vec{z} \times \vec{x} &= + \vec{y} \\ \vec{x} \times \vec{z} &= - \vec{y} \\ \end{aligned} x×yy×xy×zz×yz×xx×z=+z=−z=+x=−x=+y=−y
2.2.2 叉乘的计算
a⃗×b⃗=−b⃗×a⃗a⃗×a⃗=0⃗a⃗×(b⃗+c⃗)=a⃗×b⃗+a⃗×c⃗a⃗×(kb⃗)=k(a⃗×b⃗) \begin{aligned} \vec{a} \times \vec{b} &= - \vec{b} \times \vec{a} \\[1.25ex] \vec{a} \times \vec{a} &= \vec{0} \\[1.25ex] \vec{a} \times (\vec{b} + \vec{c}) &= \vec{a} \times \vec{b} + \vec{a} \times \vec{c}\\[1.25ex] \vec{a} \times (k\vec{b}) &= k(\vec{a} \times \vec{b}) \end{aligned} a×ba×aa×(b+c)a×(kb)=−b×a=0=a×b+a×c=k(a×b)
- 三维向量叉乘
a⃗×b⃗=(yazb−ybzazaxb−xazbxayb−yaxb) \vec{a} \times \vec{b} = \begin{pmatrix} y_a z_b - y_b z_a \\ z_a x_b - x_a z_b \\ x_a y_b - y_a x_b \end{pmatrix} a×b=⎝⎛yazb−ybzazaxb−xazbxayb−yaxb⎠⎞
- 叉乘矩阵
a⃗×b⃗=A∗b=(0−zayaza0−xa−yaxa0)(xbybzb) \vec{a} \times \vec{b} = A^*b = \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} a×b=A∗b=⎝⎛0za−ya−za0xaya−xa0⎠⎞⎝⎛xbybzb⎠⎞
2.2.3 叉乘的作用
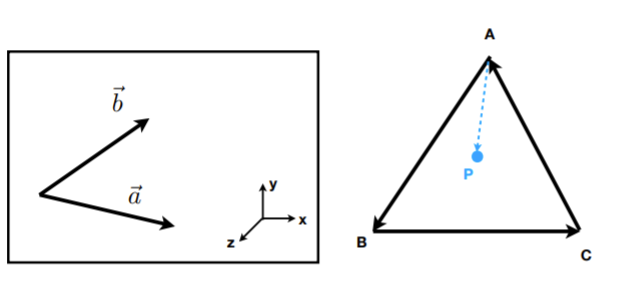
- 判断左右:利用叉乘结果的正负
- 判断内外:P点一直在三条边的左边/右边
- 图形学计算
3. 矩阵
- 矩阵的定义
- 乘法
- 运算律:结合律,分配律,没有交换律
- 转置:行列互换, aija_{ij}aij 变成 ajia_{ji}aji
- 逆:相乘为单位矩阵





 本文介绍了图形学的基础依赖学科,并详细讲解了向量的定义及其在2D和3D空间中的点乘与叉乘运算。通过具体实例解释了如何使用这些运算法则来解决图形学中常见的几何问题。
本文介绍了图形学的基础依赖学科,并详细讲解了向量的定义及其在2D和3D空间中的点乘与叉乘运算。通过具体实例解释了如何使用这些运算法则来解决图形学中常见的几何问题。
















 1696
1696

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








