本文主要讲述B树和B+树分别是什么,两者有什么区别,并且手写一下B+树。
一、B树
B树的全称叫做BalanceTree,翻译成中文也就是平衡树。平衡树是一种理论上的概念,它的思想主要是将一棵效率较低的树结构通过一系列算法转化为一个趋近于完全二叉树甚至满二叉树的过程,而B树也是树的平衡化的一种过程。
那么什么是B树呢?B树实质是一棵(N-1)-N查找树,N叫做B树的阶,B树延续了二三查找树的本质,将其结点的key进行拓展,我们知道一个结点能够存储更多的key,那么这棵树的高度也就越低,进而查找效率就会高。像B树就不会像红黑树以及二三查找树那么单一,因为一棵B树的阶数一般都会大于100甚至更大,主要用于海量数据的查找,而咱们的红黑树、二三查找树其实本质也就是一棵最简单的B树,只是此时的N=3。下面呢,咱们看一下B树的结构。

上图是一个5阶B树,单结点最多有4个key,每个结点最多只有5条子链接。
假设有一颗5阶B树,要将一组数据写入到树中。10,20,30,40,1,3,5,7,11,13,15,17,21,23,25,27,31,33,35,37,41,43,45,47
1、写入10,20,30,40
此时只有一个结点为root结点

2、写入1
root结点已经存了5个key了,咱们五阶B树一个结点最多只能存4个key。需要将其进行分解
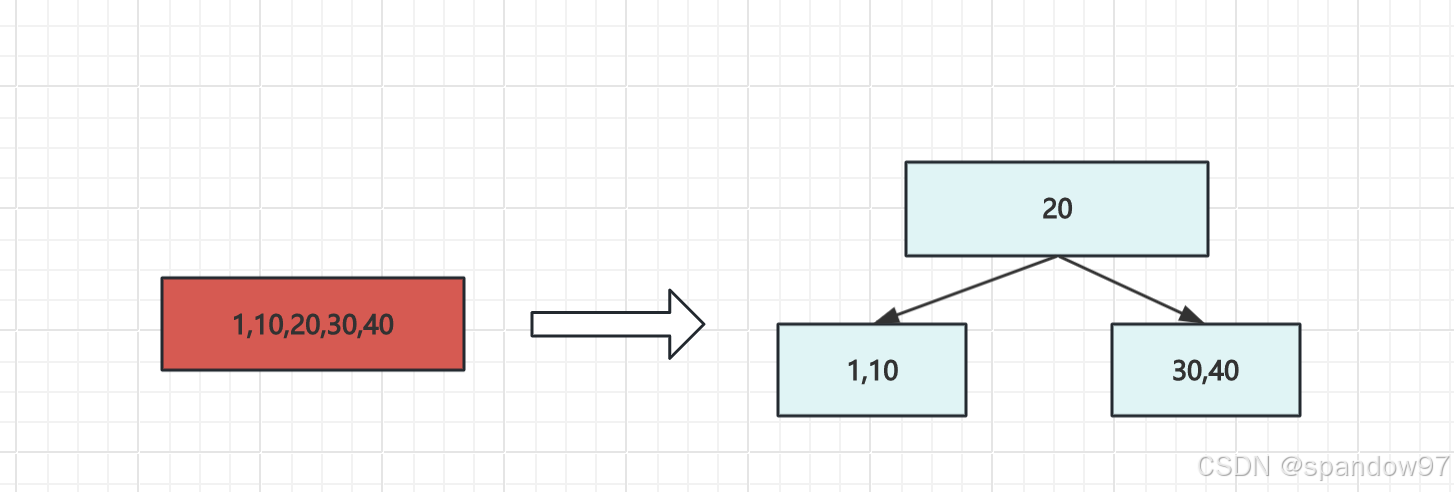
3、写入3,5,7
当插入7的时候,结点key的数量超过了4,所以需要进行分解。

4、写入11,13,15
当插入15时,结点需要进行分解。

5、写入17,21,23,25
当插入25时,需要进行分解。

6、插入27,31,33
根结点也变成了5-结点,此时将根结点进行分解,这时候根结点发生改变,咱们B+树的高度增加一层

7、继续将剩余数字写入

可以看出,B树构造就是2-3查找树的构造过程。只是相比2-3查找树咱们每个结点的key变多了,key多就代表咱们每个结点存储的数据就会更多,树的高度也就越低,查询效率自然也就得到了提升。
更多B树相关内容可参考 B树的下溢和上溢
二、B+树
B+树是在特定的场景下对B树做了优化,B树是key和data都存储在一块,这样无疑增加了内存消耗。而B+树数据是存储在当前树的叶子结点上,非叶子结点存储的只是相应的key。
一般key只是代表着数据域的索引,消耗内存比较小。其次,在(N-1)-N查找树中,每个结点的key都是有序的,所以呢,我们在每个结点可以使用二分查找快速定位到需要查找的key,然后层层递归找到咱们叶子结点中的数据。在咱们的叶子结点中,每个数据域结点又构成一个有序的单向链表。
下边是B树和B+树的内存模型图:
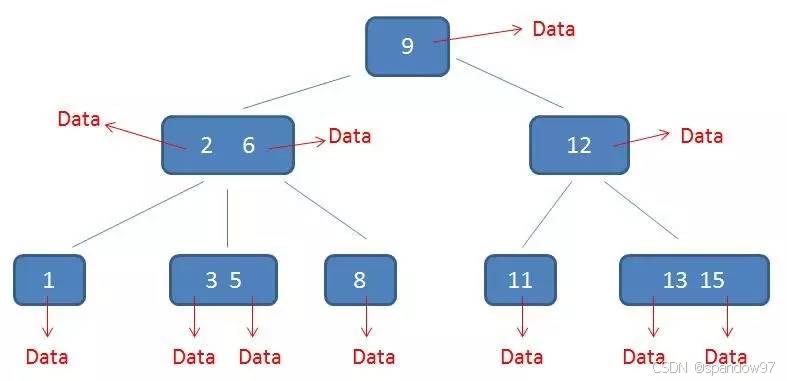
B树内存模型的结点中包含索引和data数据。

B+树内存模型只有叶子结点存储data,并且叶子结点的数据域构成有序列表。
三、B+树的代码实现
B+树的结点主要分为叶子结点和非叶子结点。它们的存储域不同,叶子结点存储键和值,非叶子结点存储键。实现的时候需要对两种结点做不同的处理。
3.1、创建结点的公共类
结点都会存储键值,所以我们把它当做公共属性放在父类中,每个结点都有至少容纳entry的个数以及最多容纳entry的个数,比如对于一个5阶B+树,每个结点最少应该存在2个key,最多应该存在4个key。
import java.util.List;
/**
* B+树节点公共类
*/
public abstract class BalancePlusTreeNode<K extends Comparable<K>, E> {
/**
* 当前节点key的集合
*/
protected List<K> entries;
/**
* 当前节点最大容纳的key数量
*/
protected static Integer UPPER_BOUND;
/**
* 当前节点最少应该包括的key数量
*/
public static Integer LOWWER_BOUND;
public BalancePlusTreeNode() {
}
public BalancePlusTreeNode(List<K> entries) {
this.entries = entries;
}
public List<K> getEntries() {
return entries;
}
public void setEntries(List<K> entries) {
this.entries = entries;
}
}3.2、定义叶子结点
在叶子结点BalancePlusTreeLeafNode中,定义data属性来表示当前叶子结点的数据域,因为它继承了结点类,所以叶子结点存在两个属性,一个entries以及data,分别来表示叶子结点所存储的键集以及数据集。使用next属性来表示构建单向链表,表示当前叶子结点的下一个结点。
/**
* 叶子节点
* @param <K>
* @param <E>
*/
public class BalancePlusTreeLeafNode<K extends Comparable<K>, E>
extends BalancePlusTreeNode<K, E> {
/**
* 当前叶子节点的数据域
*/
private List<Set<E>> data;
/**
* 叶子节点数据域的next域
*/
private BalancePlusTreeNode next;
public BalancePlusTreeLeafNode(List<K> entries, List<Set<E>> data) {
super(entries);
this.data = data;
}
}3.3、定义非叶子结点
在非结点类BalancePlusTreeNonLeafNode中,我们创建child属性来表示当前结点的子结点,因为一个非叶子结点存在不确定数量的子结点,所以我们将child设置为List类型的。
/**
* 非叶子节点
* @param <K>
* @param <E>
*/
public class BalancePlusNonLeafNode<K extends Comparable<K>, E>
extends BalancePlusTreeNode<K, E>{
/**
* 子节点的集合
*/
private List<BalancePlusTreeNode<K,E>> child;
public BalancePlusNonLeafNode(List<K> entries, List<BalancePlusTreeNode<K, E>> child) {
super(entries);
this.child = child;
}
}3.4、创建B+树的核心操作类
定义DEFAULT_BOUND来表示我们B+树的默认阶数、UPPER_BOUND表示一个结点最大的key数量、LOWER_BOUND表示一个结点最少的key数量,root表示当前B+树的根结点。并且定义两个构造方法,第一个构造方法用于让调用者传入当前B+树的阶数,主要初始化B+树结点key数量的上下限。无参构造器主要是外部没有指定阶数的时候,使用咱们B+树阶数的默认值。
/**
* B+树核心操作类
*/
public class BalancePlusTree<K extends Comparable<K>, E> {
//B+树默认的阶数
private static final Integer DEFAULT_BOUND = 4;
//上限
private static Integer UPPER_BOUND;
//下限
private static Integer LOWER_BOUND;
// 根节点
private BalancePlusTreeNode<K,E> root;
public BalancePlusTree(int bound) {
UPPER_BOUND = bound - 1;
LOWER_BOUND = UPPER_BOUND >> 1;
BalancePlusTreeNode.UPPER_BOUND = UPPER_BOUND;
BalancePlusTreeNode.LOWWER_BOUND = LOWER_BOUND;
}
public BalancePlusTree() {
this(DEFAULT_BOUND);
}
}3.5、在公共类中添加抽象put方法
public abstract BalancePlusTreeNode<K,E> put(K entry, E value);
3.6、先写一个工具类
transToList和transToSet函数将方法中的数组转成对应的集合。
splitBalancePlusTreeNode对集合按照下标范围进行切割。
/**
* B+树的工具类
*/
public class BalancePlusTreeUtil {
public static <T> List<T> transToList(T... data) {
List<T> list = new ArrayList<>();
Collections.addAll(list, data);
return list;
}
public static <E> Set<E> transToSet(E... element) {
Set<E> set = new HashSet<>();
Collections.addAll(set, element);
return set;
}
public static <T> List<T> splitBalancePlusTreeNode(List<T> splitList, int startIndex, int endIndex) {
List<T> subList = new ArrayList<>();
while(startIndex <= endIndex) {
subList.add(splitList.get(startIndex++));
}
return subList;
}
}3.7、叶子结点实现put方法
1. 查询叶子结点是否存在同样的entry,如果存在就将value添加一次;gainReplaceIndex函数可到公共类中,叶子结点和非叶子结点都可以使用。
2. 叶子结点不存在对应的key,计算出当前entry在结点中的插入位置。此函数也写到公共类中。
3. 在叶子结点中,找到entry对应位置后,咱们将当前entry以及value分别添加到对应位置即可,最后还需要判断当前叶子结点是否需要分裂。
@Override
public BalancePlusTreeNode<K, E> put(K entry, E value) {
int currentReplaceIndex = super.gainReplaceIndex(entry);
// 查询叶子结点是否存在同样的entry,如果存在就将value添加一次
if(currentReplaceIndex != -1) {
data.get(currentReplaceIndex).add(value);
return null;
}
// 不存在对应的key,此时我们应该计算出当前entry在结点中的插入位置
int currentInsertIndex = super.gainInsertIndex(entry);
entries.add(currentInsertIndex, entry);
data.add(currentInsertIndex, BalancePlusTreeUtil.transToSet(value));
// 判断当前entry数量是否到达上限,如果达到需要进行分裂
return super.isOverFlow() ? split() : null;
}
3.8、公共类中的方法
在公共类中添加三个函数:
a:判断当前key是否存在该结点的索引键列表中,存在就返回对应的下标,否则返回-1;
b:计算当前key按照顺序存储到索引键列表中的位置,并返回对应的下标;
c: 一棵N阶B+树,一个结点最多存储的entry数量最多只能为N-1个,所以我们需要判断一下当前结点entry的数量是否超过了咱们当前结点的上限;
d: 分割的时候计算分割位置可以用数组大小/2计算,>>1无符号右移运算符也相当于/2,但是位运算符的运行效率和性能要更突出。
因为索引键的集合是有序的,所以我们可以通过二分法折半去进行查找。
/**
* 二分查找法
* @param entry
* @return
*/
protected int gainReplaceIndex(K entry) {
int left = 0;
int right = entries.size() - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(entry.compareTo(entries.get(mid)) > 0) {
left = mid + 1;
}else if (entry.compareTo(entries.get(mid)) < 0) {
right = mid - 1;
}else {
return mid;
}
}
return -1;
}
/**
* 计算当前节点key的存储位置
* @param entry
* @return
*/
protected int gainInsertIndex(K entry) {
int left = 0;
int right = entries.size();
while(left < right) {
int mid = left + ((right - left) >> 1);
if(entry.compareTo(entries.get(mid)) > 0) {
left = mid + 1;
}else if(entry.compareTo(entries.get(mid)) <= 0) {
right = mid;
}
}
return left;
}
/**
* 是否超过了最大存储上限
* @return
*/
protected boolean isOverFlow() {
return entries.size() > UPPER_BOUND;
}
/**
* 分裂计算分割的位置
* @return
*/
protected int gainSplitIndex() {
return UPPER_BOUND >> 1;
}
3.9、公共类定义分裂抽象方法
叶子和非叶子结点都需要进行分裂,所以在公共类中加一个抽象方法。
protected abstract BalancePlusTreeNode<K, E> split();3.10、叶子结点实现分类方法
如果满足分裂条件,我们主要将待分裂叶子结点的entries以及data分别进行分裂,分类成两个结点,并且让前面的叶子结点的next指向后面的叶子结点。然后将,边的新结点进行返回。
@Override
protected BalancePlusTreeNode<K, E> split() {
// 分割位置
int currentSplitIndex = super.gainSplitIndex();
// 保留原先叶子结点的entry,data集合
List<K> currentSplitEntries = this.entries;
List<Set<E>> currentSplitData = this.data;
// 截取到当前index
this.entries = BalancePlusTreeUtil.splitBalancePlusTreeNode(entries, 0, currentSplitIndex);
this.data = BalancePlusTreeUtil.splitBalancePlusTreeNode(data, 0, currentSplitIndex);
// 构建新结点
List<Set<E>> splitAnotherData = BalancePlusTreeUtil.splitBalancePlusTreeNode(currentSplitData, currentSplitIndex+1, currentSplitEntries.size() - 1);
List<K> splitAnotherEntries = BalancePlusTreeUtil.splitBalancePlusTreeNode(currentSplitEntries, currentSplitIndex+1, currentSplitEntries.size() - 1);
BalancePlusTreeLeafNode<K,E> balancePlusTreeLeafNode = new BalancePlusTreeLeafNode<>(splitAnotherEntries, splitAnotherData);
// 叶子结点指向next构建
balancePlusTreeLeafNode.next = this.next;
this.next = balancePlusTreeLeafNode;
return balancePlusTreeLeafNode;
}3.11、非叶子结点的put方法
@Override
public BalancePlusTreeNode<K, E> put(K entry, E value) {
// 递归当前非叶子结点的子结点,查找到其对应的叶子结点,并完成叶子结点的添加。
BalancePlusTreeNode<K, E> insertChildNode = child.get(super.gainInsertIndex(entry)).put(entry, value);
if(insertChildNode != null) {
// 叶子结点出现分裂,叶子结点的中间entry会向上提升,非叶子结点需要存储当前的的结点entry
K newEntry = findLeafEntry(insertChildNode);
int newEntryIndex = gainInsertIndex(newEntry);
entries.add(newEntryIndex, newEntry);
child.add(newEntryIndex+1, insertChildNode);
return super.isOverFlow()? split() : null;
}
return null;
}通过递归实现查找叶子结点的key:
public K findLeafEntry(BalancePlusTreeNode<K,E> curNode) {
if(curNode instanceof BalancePlusTreeLeafNode)
return curNode.getEntries().get(0);
BalancePlusNonLeafNode<K,E> tragetNode = (BalancePlusNonLeafNode)curNode;
return findLeafEntry(child.get(0));
}3.12、非叶子结点的分裂
1、获取分裂点,也就是折中处理,让咱们的UPPER_BOUND >> 1;
2、存储当前非叶子结点的entries以及child集合;
3、让当前的非叶子结点的entries以及child改变,让其entries截取到分割点,让当前结点的child截取到分裂点的位置;
4、创建新的非叶子结点,新结点的entries则存储原非叶子结点分割点之后的entries,它的child则为分割点+1后的child集合;
5、最后再将新创建的非叶子结点返回给调用者,也就是BalancePlusTree的put方法即可。
@Override
protected BalancePlusTreeNode<K, E> split() {
int splitIndex = super.gainSplitIndex();
List<K> currentNodeEntries = entries;
List<BalancePlusTreeNode<K,E>> childList = child;
this.entries = BalancePlusTreeUtil.splitBalancePlusTreeNode(currentNodeEntries, 0, splitIndex);
this.child = BalancePlusTreeUtil.splitBalancePlusTreeNode(childList, 0, splitIndex);
List<K> rightEntries = BalancePlusTreeUtil.splitBalancePlusTreeNode(currentNodeEntries, splitIndex+1, currentNodeEntries.size()-1);
List<BalancePlusTreeNode<K,E>> rightChildren = BalancePlusTreeUtil.splitBalancePlusTreeNode(childList, splitIndex+1, childList.size()-1);
return new BalancePlusNonLeafNode<>(rightEntries, rightChildren);
}3.13、在核心类中提供put方法
public void put(K entry, E value) {
// 若root为空,创建根结点,并且此时该结点为叶子结点
if(root == null) {
List<K> entries = BalancePlusTreeUtil.transToList(entry);
List<Set<E>> data = BalancePlusTreeUtil.transToList(BalancePlusTreeUtil.transToSet(value));
root = new BalancePlusTreeLeafNode<>(entries, data);
return;
}
// 如果当前root不为空,则调用当前结点的put方法
BalancePlusTreeNode<K, E> insertNode = root.put(entry, value);
K splitRootKey = null;
if(insertNode != null) {
if(insertNode instanceof BalancePlusTreeLeafNode) {
splitRootKey = insertNode.getEntries().get(0);
}else {
splitRootKey = ((BalancePlusNonLeafNode<K,E>)insertNode).findLeafEntry(insertNode);
}
this.root = new BalancePlusNonLeafNode<K,E>(BalancePlusTreeUtil.transToList(splitRootKey), BalancePlusTreeUtil.transToList(root, insertNode));
}
}3.14、 写一个测试方法
import java.util.List;
/**
* B+树 测试类
*/
public class BalancePlusTreeTest {
public static void main(String[] args) {
System.out.println("【开始测试put方法】");
long startTime = System.currentTimeMillis();
BalancePlusTree<Integer,String> balancePlusTree = new BalancePlusTree<>(5);
balancePlusTree.put(10,"张无忌");
balancePlusTree.put(20,"周芷若");
balancePlusTree.put(30,"赵敏");
balancePlusTree.put(40,"夏诗涵");
balancePlusTree.put(1,"赵云");
balancePlusTree.put(3,"李白");
balancePlusTree.put(5,"韩信");
balancePlusTree.put(7,"瑶瑶");
balancePlusTree.put(11,"澜");
balancePlusTree.put(13,"诸葛亮");
balancePlusTree.put(15,"刘备");
balancePlusTree.put(17,"孙尚香");
balancePlusTree.put(21,"关羽");
balancePlusTree.put(23,"马超");
balancePlusTree.put(25,"貂蝉");
balancePlusTree.put(27,"小昭");
balancePlusTree.put(31,"欧阳锋");
balancePlusTree.put(33,"花木兰");
balancePlusTree.put(35,"郭靖");
balancePlusTree.put(37,"杨过");
balancePlusTree.put(41,"后羿");
balancePlusTree.put(43,"嫦娥");
balancePlusTree.put(45,"猪八戒");
balancePlusTree.put(47,"小乔");
long endTime = System.currentTimeMillis();
System.out.println("【测试结束】:一共消耗" + (endTime - startTime) + "毫秒");
}
}
运行上边的测试方法,运行正常,可通过debug的方法查看tree中结构


以上,put方法已经实现完成了。
3.15、实现query方法
B+树的精确查询比较简单,我们只需从根结点使用递归层层遍历就好。
1、在BalancePlusTreeNode中定义抽象方法query
protected abstract List<E> query(K entry);2、在叶子结点实现
@Override
protected List<E> query(K entry) {
int index = gainReplaceIndex(entry);
return index == -1? Collections.emptyList() : new ArrayList<>(data.get(index));
}3、在非叶子结点中实现
@Override
protected List<E> query(K entry) {
return child.get(gainInsertIndex(entry)).query(entry);
}4、在核心操作类中提供对外的query方法
public List<E> query(K entry) {
if(root == null) {
return Collections.emptyList();
}
return root.query(entry);
}以上我们的查询方法也实现了。
结合现有的query和put方法,可以往b+树中写入大量的数据(比如20w),然后随机去查询一个key,验证它的查询效率。(结果是很快的,耗时为ms级别)
























 2128
2128

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








