最小相位 vs 非最小相位系统：通俗解释 + 数学推导 + 可视化分析

最小相位与非最小相位系统解析

原创已于 2025-10-14 09:52:32 修改 · 631 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #算法 #开发语言

于 2025-10-14 09:35:13 首次发布

MATLAB 专栏收录该内容

75 篇文章

订阅专栏

最小相位 vs 非最小相位系统：通俗解释 + 数学推导 + 可视化分析

一、相位系统概念回顾

在控制系统和信号处理中，相位（phase） 描述了系统对输入信号的时间延迟特性。系统的“最小相位”与“非最小相位”之分，源于其 零点分布 和 相位特性 的差异。这种差异不仅影响系统的频域相位响应，也直接影响到系统的时域动态特性和可控性。

二、通俗理解

（1）最小相位系统

想象一个反应迅速的运动员：

起跑即向前冲；
响应快速直接；
能量集中在响应初期；
行为可预测。

数学特征：所有零点都位于复平面左半部（连续系统）或单位圆内（离散系统）。

（2）非最小相位系统

想象一个先退后进的运动员：

起跑时先后仰或反向动作；
初始响应方向与最终目标相反；
出现“反向”或“过冲”现象；
响应速度较慢。

数学特征：至少有一个零点位于复平面右半部（连续系统）或单位圆外（离散系统）。

三、数学推导与理论证明

1. 传递函数定义

设系统传递函数为：

$G(s)=K(s−z1)(s−z2)⋯(s−zm)(s−p1)(s−p2)⋯(s−pn)G(s)=K\frac{(s-z_1)(s-z_2)\cdots(s-z_m)}{(s-p_1)(s-p_2)\cdots(s-p_n)}$

其中 $z_i$ 为零点， $p_i$ 为极点。

若所有零点满足 $Re(zi)<0\mathrm{Re}(z_i)<0$ ，则称系统为最小相位系统；若存在 $Re(zi)>0\mathrm{Re}(z_i)>0$ ，则为非最小相位系统。

2. 相位与幅值的解析关系（Hilbert变换）

在连续时间系统中，最小相位系统的相位与幅值之间满足 Hilbert变换 关系：

$ϕ(ω)=−Hln⁡∣G(jω)∣\phi(\omega)=-\mathcal{H}{\ln|G(j\omega)|}$

也就是说，最小相位系统的相位响应完全由幅频特性唯一确定。

若系统存在右半平面零点，则相位响应将比最小相位系统额外滞后。

设有右半平面零点 $z_0>0$ ，对应的相位附加量为：

$Δϕ(ω)=−2tan⁡−1(ωz0)\Delta\phi(\omega)=-2\tan^{-1}\left(\frac{\omega}{z_0}\right)$

此即“非最小相位系统的相位滞后附加量”，说明即使幅频特性相同，非最小相位系统的相位也更滞后。

3. 时域响应差异

以阶跃输入 $u (t) = 1 (t)$ 为例：

$Y(s)=G(s)⋅1sY(s)=G(s)\cdot\frac{1}{s}$

若 $G (s)$ 为最小相位系统，其响应单调上升趋稳；而若 $G (s)$ 含右半平面零点，则初期导数为负，即输出先向反方向偏移后再回归正向稳态。

从数学上看，若传递函数为：

$G1(s)=s+as2+2s+2,a>0G_1(s)=\frac{s+a}{s^2+2s+2},\quad a>0$

与

$G2(s)=−s+as2+2s+2G_2(s)=\frac{-s+a}{s^2+2s+2}$

则两者在极点相同的情况下， $G_2(s)$ 的零点位于右半平面，导致其时域响应初期反向。

四、MATLAB 可视化验证代码

%% 最小相位 vs 非最小相位系统可视化
% 作者：基于用户需求生成
% 日期：当前日期

clear; close all; clc;

%% 定义系统
t = 0:0.01:10;

% 最小相位系统
num_min = [1, 1];
den_min = [1, 2, 2];
sys_min = tf(num_min, den_min);

% 非最小相位系统
num_nonmin = [-1, 1];
den_nonmin = [1, 2, 2];
sys_nonmin = tf(num_nonmin, den_nonmin);

%% 时域响应分析
figure('Position', [100, 100, 1200, 800]);

subplot(2,3,1);
step(sys_min, 'b', sys_nonmin, 'r', t);
title('阶跃响应比较');
legend('最小相位系统', '非最小相位系统', 'Location', 'best');
grid on; ylabel('幅度');

subplot(2,3,2);
impulse(sys_min, 'b', sys_nonmin, 'r', t);
title('脉冲响应比较');
legend('最小相位系统', '非最小相位系统', 'Location', 'best');
grid on; ylabel('幅度');

subplot(2,3,3);
freq = 0.5;
u_sin = sin(2*pi*freq*t);
y_min_sin = lsim(sys_min, u_sin, t);
y_nonmin_sin = lsim(sys_nonmin, u_sin, t);
plot(t, u_sin, 'g--', t, y_min_sin, 'b', t, y_nonmin_sin, 'r');
title('正弦输入响应 (0.5 Hz)');
legend('输入', '最小相位', '非最小相位', 'Location', 'best');
grid on; xlabel('时间 (s)'); ylabel('幅度');

subplot(2,3,4);
[mag_min, phase_min, w_min] = bode(sys_min);
[mag_nonmin, phase_nonmin, w_nonmin] = bode(sys_nonmin);
semilogx(w_min, 20*log10(squeeze(mag_min)), 'b', 'LineWidth', 2);
hold on;
semilogx(w_nonmin, 20*log10(squeeze(mag_nonmin)), 'r', 'LineWidth', 2);
title('幅频特性 (Bode图)');
legend('最小相位', '非最小相位', 'Location', 'best');
grid on; ylabel('幅度 (dB)');

subplot(2,3,5);
semilogx(w_min, squeeze(phase_min), 'b', 'LineWidth', 2);
hold on;
semilogx(w_nonmin, squeeze(phase_nonmin), 'r', 'LineWidth', 2);
title('相频特性 (Bode图)');
legend('最小相位', '非最小相位', 'Location', 'best');
grid on; xlabel('频率 (rad/s)'); ylabel('相位 (度)');

subplot(2,3,6);
pzmap(sys_min, 'b', sys_nonmin, 'r');
title('零极点分布');
legend('最小相位', '非最小相位', 'Location', 'best');
grid on;

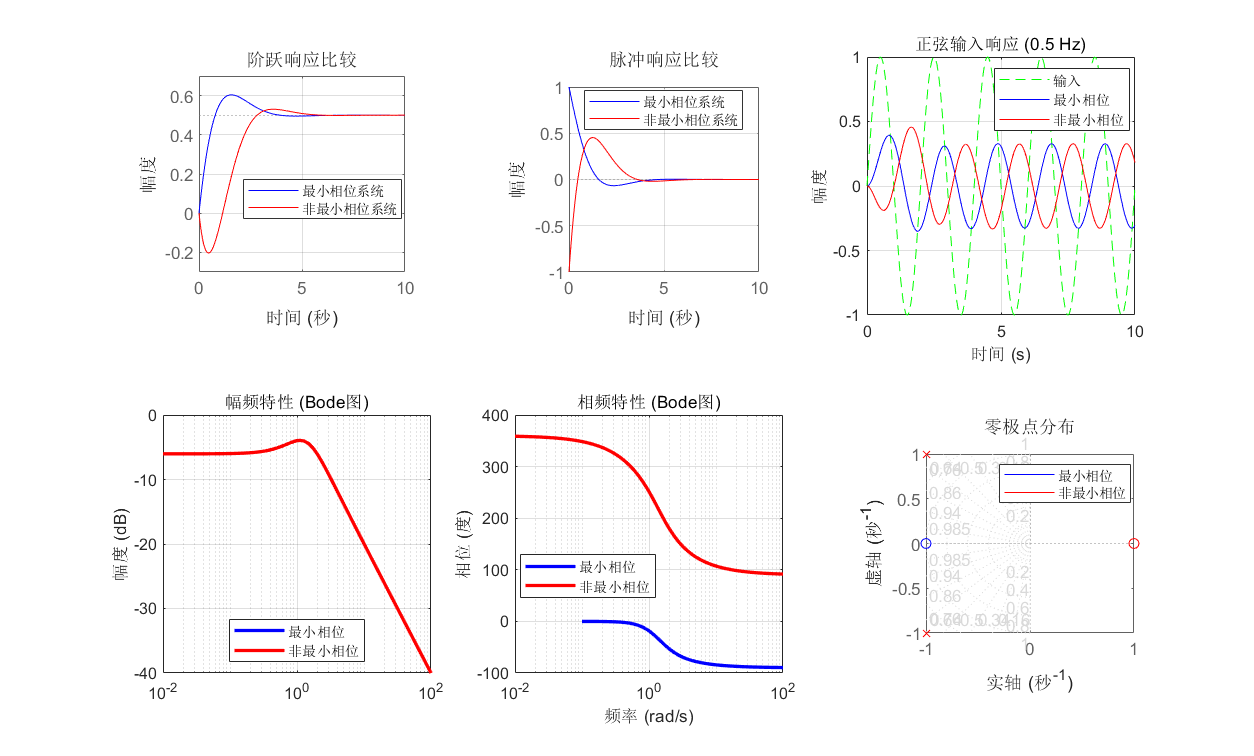
在这里插入图片描述

五、结果分析与总结

通过仿真可得：

特性	最小相位系统	非最小相位系统
零点位置	左半平面	右半平面
阶跃响应	单调上升	初期反向响应
能量分布	前段集中	分布较散
相位特性	相位滞后小	相位滞后大

从数学与仿真结果可见：

非最小相位系统的右半平面零点引入附加相位滞后；
系统的因果性与可逆性在最小相位系统中最优；
在控制设计中，非最小相位系统会增加闭环带宽受限与超调风险。

六、应用场景

系统类型	常见应用
最小相位系统	音频均衡器、控制系统、通信滤波器
非最小相位系统	化工过程、经济系统、存在延迟或逆响应的系统

结论：理解最小相位与非最小相位的数学与物理意义，对于系统稳定性分析、频率补偿、信号处理与控制器设计至关重要。