[Jzoj] 2196.生成树

题目描述

有一种图形叫做五角形圈。一个五角形圈的中心有$1$个由$n$个顶点和$n$条边组成的圈。在中心的这个$n$边圈的每一条边同时也是某一个五角形的一条边，一共有$n$个不同的五角形。这些五角形只在五角形圈的中心的圈上有公共的顶点。

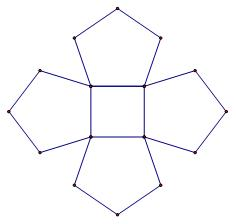
如图所示是一个$4$-五角形圈。

现在给定一个$n$五角形圈，你的任务就是求出$n$五角形圈的不同生成树的数目。还记得什么是图的生成树吗？一个图的生成树是保留原图的所有顶点以及顶点的数目减去一这么多条边,从而生成的一棵树。
　　
注意：在给定的$n$五角形圈中所有顶点均视为不同的顶点。
　

题目解析

如果$n$个五边形每个断掉一条边就会得到一个基环外向树

此时还需要断掉一条边，所以$n$个五边形中就有一个五边形要断掉两条边，并且容易想到有一条必然是在中心的那个$n$
边形上

从$n$个五边形中选取一个是选两条边的，这个五边形在中央$n$边形上那条边必选，那么只需在剩下$4$条边再断一条即可，而剩下的$n-1$个五边形都是随便断一条即可，总方案数就是$4\ast n\ast 5^n$${}^{-}$${}^1$

代码

#include<bits/stdc++.h>
using namespace std;
int T,n,ans,M=2007;
int main()
{
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
	scanf("%d",&T);
	while(T--)
	{
	  scanf("%d",&n);
	  ans=4*n%M;
	  for(int i=1;i<n;i++)
	   (ans*=5)%=M;
	  printf("%d\n",ans);
	}
}