周志华版机器学习第三章习题答案

原文参考链接：[https://blog.youkuaiyun.com/icefire_tyh/article/details/52064910]
习题
3.1

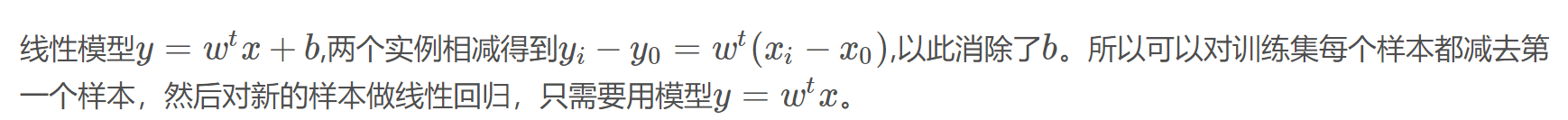
3.2
如果一个多元函数是凸的，那么它的Hessian矩阵是半正定的

3.3

#导入需要的包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
#导入数据
data = np.array([[0.697, 0.460, 1],
        [0.774, 0.376, 1],
        [0.634, 0.264, 1],
        [0.608, 0.318, 1],
        [0.556, 0.215, 1],
        [0.403, 0.237, 1],
        [0.481, 0.149, 1],
        [0.437, 0.211, 1],
        [0.666, 0.091, 0],
        [0.243, 0.267, 0],
        [0.245, 0.057, 0],
        [0.343, 0.099, 0],
        [0.639, 0.161, 0],
        [0.657, 0.198, 0],
        [0.360, 0.370, 0],
        [0.593, 0.042, 0],
        [0.719, 0.103, 0]])
定义变量
X = data[:,0:2]
y = data[:,2]
#随机划分训练集和测试集
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.25,random_state=33)
 #定义sigmoid
def sigmoid(z): 
    s = 1 / (1 + np.exp(-z))
    return s
def initialize_with_zeros(dim):
    """
    This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
    """
    w = np.zeros((dim, 1))
    b = 0
    assert (w.shape == (dim, 1))
    assert (isinstance(b, float) or isinstance(b, int))
    return w, b

def propagate(w, b, X, Y):
    """
    Implement the cost function and its gradient for the propagation explained above
    """
    m = X.shape[1]
    A = sigmoid(np.dot(w.T, X) + b)
      # 计算损失
    cost = -np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))/ m  
  
    dw = np.dot(X, (A - Y).T) / m
    db = np.sum(A - Y) / m

    assert (dw.shape == w.shape)
    assert (db.dtype == float)
    cost = np.squeeze(cost)
    assert (cost.shape == ())

    grads = {
   "dw": dw,
             "db": db}