63. 不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？ 来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/unique-paths-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize){
    int row = obstacleGridSize;
    int line = obstacleGridColSize[0];
    if(obstacleGrid[0][0] == 1 || obstacleGrid == NULL)
    {
        return 0;
    }

    int **dp = (int**)malloc(sizeof(int*) * row);
    for(int i = 0; i < row; i++)
    {
        int *temp = (int*)malloc(sizeof(int) * line);
        dp[i] = temp;
    }

    dp[0][0] = 1;
    for(int i = 1; i < row; i++)
    {
        if(obstacleGrid[i][0] == 1 || dp[i-1][0] == 0) //如果在边缘处遇到障碍，后面都去不了
        {
            dp[i][0] = 0;
        }
        else
        {
            dp[i][0] = 1;
        }
    }

    for(int i = 1; i < line; i++)
    {
        if(obstacleGrid[0][i] == 1 || dp[0][i-1] == 0) //如果在边缘处遇到障碍，后面都去不了
        {
            dp[0][i] = 0;
        }
        else
        {
            dp[0][i] = 1;
        }
    }

    for(int i = 1; i < row; i++)
    {
        for(int j = 1; j < line; j++)
        {
            if(obstacleGrid[i][j] == 1)  //如果当前为障碍，则路径数为0
            {
                dp[i][j] = 0;
            }
            else
            {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
    }

    return dp[row-1][line-1];

}

思路：动态规划
这道题与62基本一致，只不过是多了一个障碍，障碍可以考虑为当前路径数为0。假如在右边际和上边际处遇到障碍，则后面的路径都为0：

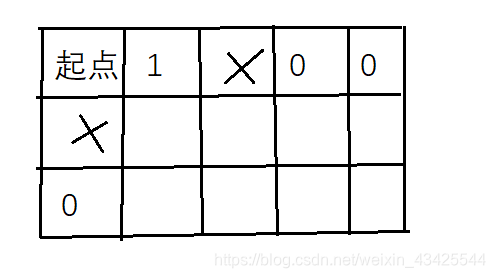
其他的思路和62一致：