P3374 【模板】树状数组 1

树状数组也是一种分块数组，终极理解在这张图上（网上偷的）

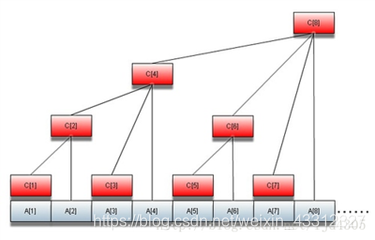
可以看到，每2^i个a[i]就有一个管理这一块矩阵值的c[i]。而且有
x+lowbit(x)为x对应父节点的下标
x-lowbit(x)为x所管辖块的前一块的父节点的下标
tree[i]储存值，而且取了前缀和summ(x)后，还可以很轻松地完成区间和的查询

但是树状数组的限制就在：只能求前缀问题和差分问题。所以更广的应用还是在线段树上

#include<bits/stdc++.h>
#define maxn 500005
#define lowbit(x) ((x)&(-x))
typedef long long ll;
using namespace std;
ll tree[maxn]={0};
int n,m;
void aupdate(ll x, ll k){
    while(x<=n){
        tree[x]+=k;
        x+=lowbit(x);
    }
}

ll summ(ll x){
    ll ans=0;
    while(x!=0){
        ans+=tree[x];
        x-=lowbit(x);
    }
    return ans;
}

ll query(ll x,ll y){
    return summ(y)-summ(x-1);
}
int main(void){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        ll ai;
        scanf("%lld",&ai);
        aupdate(i,ai);
    }

    while(m--){
        int op;
        ll x,y,k;
        scanf("%d",&op);
        switch(op){
            case 1:
                scanf("%lld%lld",&x,&k);
                aupdate(x,k);
                break;
            case 2:
                scanf("%lld%lld",&x,&y);
                printf("%lld\n",query(x,y));
                break;
            default:
                break;
        }

    }
}