理解slam中的非线性优化问题

主要参考了高翔老师的14讲中的知识，以及结合imu预积分论文（On-manifold preintegration for real-time visual-inertial Odometry），结合自己的理解，做了一下整理。

整体思路是从状态估计——最大后验估计——最小二乘——非线性最小二乘

状态估计——最大后验估计

非线性优化在slam中的应用是对物体自身的状态估计，状态变量为Xi=[Ri , pi , vi , bi ] ，这几个变量分别时旋转、平移、速度和偏置。状态估计问题就是在已知传感器输入u，和观测数据z时，对Xi的条件概率分布进行估计。
现在只考虑观测数据对状态变量的影响，即计算p (Xk |Zk ），Xk 表示所有关键帧的状态，Zk={Ci , Iij} ，(i,j )∈Kk，Ci为相机在i时刻的测量值，Iij为从i到j时刻imu的测量数据。根据最大后验估计（MAP）,
p (Xk |Zk ）=p (Zk |Xk )p (X0），p (X0）为先验，即已知的物体状态。最后化简为

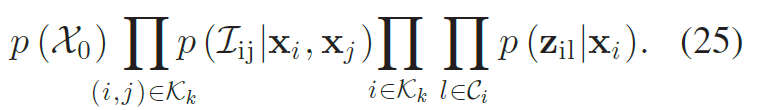
最大后验估计——最小二乘

对于最大后验估计，我们的目的是最大化概率p (Xk |Zk ）。观测方程的表达假定为Zk=h(Xk)+Vij，假定噪声Vij服从零均值的高斯分布，其协方差为Σ，Vij~N(0,Σ)。
那么对于p (Zk |Xk )=N（h(Xk)，Σ)，这仍然是一个高斯分布。计算Xk使得这个概率分布趋于最大，使用最小化负对数的方法。
考虑一个高斯分布x~N(u,Σ)，其概率密度函数的展开形式为