二阶系统响应指标图_一阶和二阶系统的动态特性参数

检测系统的时域动态性能指标一般都是用阶跃输入时检测系统的输出响应，即过渡过程曲线上的特性参数来表示。

1．一阶系统的时域动态特性参数

一阶测量系统时域动态特性参数主要是时间常数及与之相关的输出响应时间。

(1)时间常数

时间常数是一阶系统的最重要的动态性能指标，一阶测量系统为阶跃输入时，其输出量上升到稳态值的63.2％所需的时间，就为时问常数

。一阶测量系统为阶跃输入时响应曲线的初始斜率为1／

。

(2)响应时间

当系统阶跃输入的幅值为a时，对一阶测量系统传递函数式(1-54)进行拉氏反变换，得一阶测量系统的对阶跃输入的输出响应表达式为

(1)

其输出响应曲线如图1所示。

从式(1)和图1，可知一阶测量系统响应y(t)随时间t增加而增大，当t=∞时趋于最终稳态值，即y(∞)=ka。理论上，在阶跃输入后的任何具体时刻都不能得到系统的最终稳态值，即总是y (t(这时有一阶测量系统的输出y (4τ)≈ y (∞)×98.2％=0．982ka)当作一阶测量系统对阶跃输入的输出响应时间。一阶检测系统的时间常数越小，其系统输出的响应就越快。顺便指出，在某些实际工程应用中根据具体测量和试验需要，也有把tr=5

或tr=3

作为一阶测量系统对阶跃输入输出响应时间的情况。

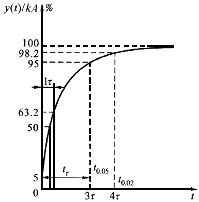
图1 一阶测量系统对阶跃输入的响应

2．二阶系统的时域动态特性参数和性能指标

对二阶测量系统，当输入信号x(t)为幅值等于a的阶跃信号时，通过对二阶测量系统传递函数式进行拉氏反变换，可得常见二阶测量系统(通常有0<

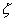<1，称为欠阻尼)的对阶跃输入的输出响应表达式

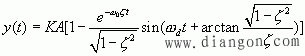
上式右边括号外的系数与一阶测量系统阶跃输入时的响应相同，其全部输出由二项叠加而成。其中一项为不随时间变化的稳态响应ka，另一项为幅值随时间变化的阻尼衰减振荡(暂态响应)。暂态响应的振荡角频率wd称为系统有阻尼自然振荡角频率。暂态响应的幅值按指数

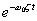规律衰减，阻尼比善愈大暂态幅值衰减愈快。如果

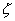=0，则二阶测量系统对阶跃的响应将为等幅无阻尼振荡；如果

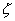=1，称为临界阻尼，这时二阶测量系统对阶跃的响应为稳态响应ka叠加上一项幅值随时间作指数减少的暂态项，系统响应无振荡；如果

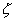>;1，称为过阻尼，其暂态响应为两个幅值随时间作指数减少的暂态项，且因其中一个衰减很快(通常可忽略其影响)。整个系统响应与一阶系统对阶跃输入响应相近，可把其近似地作为一阶系统分析对待。在阶跃输入下，不同阻尼比对(二阶测量)系统响应的影响如图2所示。

图2 阶跃输入下，二阶测量(不同阻尼比对)响应

可见，阻尼比

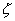和系统有阻尼自然振荡角频率

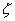是二阶测量系统最主要的动态时域特性参数。常见0<

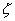<1衰减振荡型二阶系统的时域动态性能指标示意图如图3所示。表征二阶测量系统在阶跃输入作用下时域主要性能指标主要如下：

(1)延迟时间td系统输出响应值达到稳态值的50％所需的时间，称为延迟时间。

(2)上升时间tr系统输出响应值从10％到达90％稳态值所需的时间，称为上升时间。

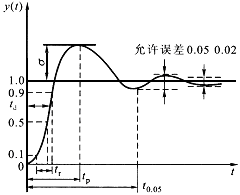
图3 二阶系统的时域动态性能指标不恿图

(3)响应时间ts在响应曲线上，系统输出响应达到一个允许误差范围的稳态值，并永远保持在这一允许误差范围内所需的最小时间，称为响应时间。根据不同的应用要求，允许误差范围取值不同，对应的响应时间也不同。工程中多数选系统输出响应第一次到达稳态值的95％或98％(也即允许误差为±5％或±2％)的时间为响应时间。

(4)峰值时间tp输出响应曲线达到第一个峰值所需的时间，称为峰值时间。因为峰值时间与超调量相对应，所以峰值时间等于阻尼振荡周期的一半，即tp=t／2。

(5)超调量σ超调量为输出响应曲线的最大偏差与稳态值比值的百分数，即

σ=[ y (tp)-y(∞)]／y(∞)×100％

(6)衰减率d 衰减振荡型二阶系统过渡过程曲线上相差一个周期t的两个峰值之比称为衰减率。

上述衰减振荡型二阶检测系统的动态性能指标、相互关系及计算公式如表1所示。

表1 0<

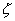<1二阶检测系统时域动态性能指标

3．检测系统的频域动态性能指标

检测系统的频域动态性能指标由检测系统的幅频特性和相频特性的特性参数来表示，主要有通频带与工作频带以及系统固有角频率。

(1)系统的通频带与工作频带

如果一个检测系统，其输出y(t)与输入x(t)之间满足

y(t)=ax(t-τ) (2)

即系统的输出与输入之间有一个数值为a的固定放大倍数和相移为

的延时。这样的系统称为完全不失真系统。在工程上，完全不失真系统难于实现。一些设计较好的检测系统通常也只在一定的频度范围内使幅频特性曲线保持一段较为平坦的近似水平的线段(在这一范围a近似不变)。工程上，把幅频放大倍数大于

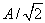的范围叫通频带。而检测系统的相频特性近似线性的范围一般比通频带小得多。为使检测系统有较高的精度，应选检测系统相频特性近似线性或幅频特性近似水平的频率范围为系统的工作频带。

(2)系统的固有频率

当|h(jω)|= |h(jω)|max时所对应的频率称为系统固有角频率w0。知道和确定了检测系统的固有角频率w0，就可以确定该系统可测信号的频率范围，以保证测量获得较高的精度，这在设计和选用检测仪器和检测系统时是非常重要的。