IMU初始化是为了给局部BA和全局BA提供一个更好的初值从而减少IMU噪声积累。
IMU初始化分解为多个子问题:
- 估计陀螺仪偏置
- 忽略加速度计偏置,估计尺度和重力矢量
- 估计加速度计偏置,进一步优化尺度和重力
- 估计速度
1. 陀螺仪偏置估计
初始化过程假定bgb^gbg保持不变,每帧的偏置恒定:big=bgb_i^g=b^gbig=bg。优化bgb^gbg,最小化所有相邻关键帧对之间的陀螺仪(旋转)预积分及从纯视觉ORB-SLAM2直接视觉计算的旋转之间的误差。
∗bg=argminθ∑k=1N−1∥Log((ΔR~k,k+1Exp(JΔgbg))TRBWk+1RWBk)∥2
^*b^g=\mathop{\arg\min}_{\theta} \sum_{k=1}^{N-1}\|Log((\Delta\tilde{R}_{k,k+1}Exp(J_{\Delta}^{g}b^g))^TR_{BW}^{k+1}R_{WB}^{k})\|^2
∗bg=argminθk=1∑N−1∥Log((ΔR~k,k+1Exp(JΔgbg))TRBWk+1RWBk)∥2 其中ΔR~k,k+1=Exp((ωk~−bg)Δt)\Delta\tilde{R}_{k,k+1}=Exp((\tilde{\omega_k}-b^g)\Delta t)ΔR~k,k+1=Exp((ωk~−bg)Δt),为陀螺仪的预积分值。N为关键帧的数量。RWB(⋅)=RWC(⋅)×RCB(⋅)R_{WB}^{(·)}=R_{WC}^{(·)}\times R_{CB}^{(·)}RWB(⋅)=RWC(⋅)×RCB(⋅),RWC(⋅)R_{WC}^{(·)}RWC(⋅)为ORB-SLAM视觉计算的位姿,RCB(⋅)R_{CB}^{(·)}RCB(⋅)由标定得到。bgb^gbg从0开始迭代。
2.尺度及重力估计
忽略加速度计偏置bia=ba=0b_i^a=b^a=0bia=ba=0,由第一步得到的陀螺仪偏置,可以预积分速度及位移Δvij,Δpij\Delta{v_{ij}},\Delta{p_{ij}}Δvij,Δpij:
Δvij=∑k=ij−1ΔRika~kΔtΔpij=∑k=ij−1ΔvikΔt+12ΔRika~kΔt2ΔRij=∏k=ij−1Exp((w~k−bg)Δt)\Delta{v_{ij}}=\sum_{k=i}^{j-1}{\Delta R_{ik}\tilde{a}_k\Delta t} \\
\Delta{p_{ij}}=\sum_{k=i}^{j-1}{\Delta v_{ik} \Delta t+\frac{1}{2} \Delta R_{ik}\tilde{a}_k\Delta t^2} \\
\Delta{R_{ij}}=\prod_{k=i}^{j-1}{Exp((\tilde{w}_k-b^g)\Delta t)}Δvij=k=i∑j−1ΔRika~kΔtΔpij=k=i∑j−1ΔvikΔt+21ΔRika~kΔt2ΔRij=k=i∏j−1Exp((w~k−bg)Δt)
视觉观测尺度不确定,有TWC=[RWCsWpC0T1]T_{WC}=\left[ \begin{array}{} R_{WC} & s_Wp_C\\ 0^T & 1 \end{array}\right ]TWC=[RWC0TsWpC1],因此,由camera系到body系的转化过程中,有:
TWB=[RWBWpB0T1]=TWCTCB=[RWCsWpC0T1]⋅[RCBCpB0T1]=[RWCRCBRWCCpB+sWpC0T1]T_{WB}=\left[ \begin{array}{} R_{WB} & _Wp_B\\ 0^T & 1 \end{array}\right ]=T_{WC}T_{CB}=\left[ \begin{array}{} R_{WC} & s_Wp_C\\ 0^T & 1 \end{array}\right ]·\left[ \begin{array}{} R_{CB} & _Cp_B\\ 0^T & 1 \end{array}\right ]=\left[ \begin{array}{} R_{WC}R_{CB} & R_{WC}{_Cp_B}+{s_Wp_C}\\ 0^T & 1 \end{array}\right ]TWB=[RWB0TWpB1]=TWCTCB=[RWC0TsWpC1]⋅[RCB0TCpB1]=[RWCRCB0TRWCCpB+sWpC1] 其中TCBT_{CB}TCB为标定得到,即WpB=RWCCpB+sWpC_Wp_B=R_{WC}{_Cp_B}+{s_Wp_C}WpB=RWCCpB+sWpC 代入位置关联方程:
WpBi+1=WpBi+WvBiΔti,i+1+12gWΔti,i+12+RWBiΔpi,i+1_Wp_{B}^{i+1}=_Wp_{B}^{i}+_Wv_{B}^{i}\Delta t_{i,i+1}+\frac12g_W\Delta t_{i,i+1}^2+R_{WB}^i\Delta p_{i,i+1}WpBi+1=WpBi+WvBiΔti,i+1+21gWΔti,i+12+RWBiΔpi,i+1 得到:sWpCi+1=sWpCi+WvBiΔti,i+1+12gWΔti,i+12+RWBiΔpi,i+1+(RWCi−RWCi+1)CpBs_Wp_{C}^{i+1}=s_Wp_{C}^{i}+_Wv_{B}^{i}\Delta t_{i,i+1}+\frac12g_W\Delta t_{i,i+1}^2+R_{WB}^i\Delta p_{i,i+1}+(R_{WC}^i-R_{WC}^{i+1}){_Cp_B}sWpCi+1=sWpCi+WvBiΔti,i+1+21gWΔti,i+12+RWBiΔpi,i+1+(RWCi−RWCi+1)CpB 其中,WpCi,RWCi,RWCi+1,WpCi+1_Wp_{C}^{i},R_{WC}^i,R_{WC}^{i+1},_Wp_{C}^{i+1}WpCi,RWCi,RWCi+1,WpCi+1由视觉计算得到,Δti,i+1\Delta t_{i,i+1}Δti,i+1已知,Δpi,i+1\Delta p_{i,i+1}Δpi,i+1由预积分得到,RCB,CpBR_{CB},_Cp_BRCB,CpB为标定得到。解该线性方程组得到s、gWs、g_Ws、gW,然而方程中含有WvBi_Wv_B^iWvBi,为避免计算这N个速度,降低复杂度。我们将连续的三帧提取两个关系,利用速度关联方程:WvBi+1=WvBi+gWΔti,i+1+RWBiΔvi,i+1_Wv_{B}^{i+1}=_Wv_{B}^{i}+g_W\Delta t_{i,i+1}+R_{WB}^i\Delta v_{i,i+1}WvBi+1=WvBi+gWΔti,i+1+RWBiΔvi,i+1 为简化表述,使用1,2,3代替i,i+1,i+2i,i+1,i+2i,i+1,i+2,有:
sWpC3=sWpC2+WvB2Δt23+12gWΔt232+RWB2Δp23+(RWC2−RWC3)CpBsWpC2=sWpC1+WvB1Δt12+12gWΔt122+RWB1Δp12+(RWC1−RWC2)CpBWvB2=WvB1+gWΔt12+RWB1Δv12s_Wp_{C}^{3}=s_Wp_{C}^{2}+_Wv_{B}^{2}\Delta t_{23}+\frac12g_W\Delta t_{23}^2+R_{WB}^2\Delta p_{23}+(R_{WC}^2-R_{WC}^{3}){_Cp_B} \\
{s_Wp_{C}^{2}=s_Wp_{C}^{1}+_Wv_{B}^{1}\Delta t_{12}+\frac12g_W\Delta t_{12}^2+R_{WB}^1\Delta p_{12}+(R_{WC}^1-R_{WC}^{2}){_Cp_B}} \\
{_Wv_{B}^{2}=_Wv_{B}^{1}+g_W\Delta t_{12}+R_{WB}^1\Delta v_{12}}sWpC3=sWpC2+WvB2Δt23+21gWΔt232+RWB2Δp23+(RWC2−RWC3)CpBsWpC2=sWpC1+WvB1Δt12+21gWΔt122+RWB1Δp12+(RWC1−RWC2)CpBWvB2=WvB1+gWΔt12+RWB1Δv12 第一式乘Δt12\Delta t_{12}Δt12与第二式乘Δt23\Delta t_{23}Δt23做差,结合代入第三式,得到:
(λ(i)β(i))(sgW)=γ(i)\left( \begin{array}{} \lambda(i)&\beta(i) \end{array}\right )\left( \begin{array}{} s\\g_W \end{array}\right )=\gamma(i)(λ(i)β(i))(sgW)=γ(i)
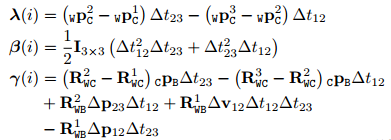
3.加速度计偏置估计及尺度、重力修正
由于在之前的估计中忽略了加速度计偏置,导致我们计算的重力实际上也混杂了偏置的影响,与实际的重力方向有偏差。引入惯性系III以及实际重力GGG,在惯性系下实际重力的方向向量坐标为g^I=(0,0,−1)\hat{g}_I=(0,0,-1)g^I=(0,0,−1),我们估计的重力在世界系下的方向为gW^=gW∗∥gW∗∥\hat{g_W}=\frac{g_W^*}{\|g_W^*\|}gW^=∥gW∗∥gW∗.由此,我们可以计算惯性系到世界系的旋转矩阵:
RWI=Exp(v^θ)v^=g^I×g^W∥g^I×g^W∥ , θ=atan2(∥g^I×g^W∥,g^I⋅g^W)R_{WI}=Exp(\hat v\theta) \\
\hat v=\frac{\hat g_I×\hat{g}_W}{\|\hat g_I×\hat{g}_W\|} \ , \ \theta=atan2({\|\hat g_I×\hat{g}_W\|},\hat g_I·\hat{g}_W)RWI=Exp(v^θ)v^=∥g^I×g^W∥g^I×g^W , θ=atan2(∥g^I×g^W∥,g^I⋅g^W) 将实际重力惯性系坐标旋转到世界系中,即实际重力在世界系下的坐标为gW=RWIg^IGg_W=R_{WI}\hat{g}_IGgW=RWIg^IG 但是由于我们估计的重力与实际重力是有偏差的,所以旋转矩阵RWIR_{WI}RWI并不是实际两坐标系的旋转矩阵,需要加一个修正量δθ\delta\thetaδθ。
另外由于惯性系中重力方向沿z方向,所以沿z轴的旋转是没有影响的。旋转轴在xy平面,只有沿x轴与y轴的旋转分量,没有z轴的旋转分量,即δθ=(δθx δθy 0)T\delta\theta=(\delta\theta_x \ \delta\theta_y \ 0)^Tδθ=(δθx δθy 0)T,综上,有:gW=RWIExp(δθ)g^IGδθ=(δθxyT 0)T=(δθx δθy 0)Tg_W=R_{WI}Exp(\delta\theta)\hat{g}_IG \\ \delta\theta=(\delta\theta_{xy}^T \ 0)^T=(\delta\theta_x \ \delta\theta_y \ 0)^TgW=RWIExp(δθ)g^IGδθ=(δθxyT 0)T=(δθx δθy 0)T 一阶近似gW≃RWI(I+δθ∧)g^IG=RWIg^IG−RWIg^I∧Gδθg_W\simeq R_{WI}(I+\delta\theta^{\wedge})\hat{g}_IG=R_{WI}\hat{g}_IG-R_{WI}\hat{g}_I^{\wedge}G\delta\thetagW≃RWI(I+δθ∧)g^IG=RWIg^IG−RWIg^I∧Gδθ 除了引入重力修正,我们同时考虑加速度计偏置的影响。代入位置关联方程:sWpCi+1=sWpCi+WvBiΔti,i+1−12RWIg^I∧GΔti,i+12δθ+RWBi(Δpi,i+1+JΔpaba)+(RWCi−RWCi+1)CpB+12RWIg^IGΔti,i+12s_Wp_{C}^{i+1}=s_Wp_{C}^{i}+_Wv_{B}^{i}\Delta t_{i,i+1}-\frac12R_{WI}\hat{g}_I^{\wedge}G\Delta t_{i,i+1}^2\delta\theta+R_{WB}^i(\Delta p_{i,i+1}+J_{\Delta p}^ab^a)+(R_{WC}^i-R_{WC}^{i+1}){_Cp_B}+\frac12R_{WI}\hat{g}_IG\Delta t_{i,i+1}^2sWpCi+1=sWpCi+WvBiΔti,i+1−21RWIg^I∧GΔti,i+12δθ+RWBi(Δpi,i+1+JΔpaba)+(RWCi−RWCi+1)CpB+21RWIg^IGΔti,i+12 这样,我们就引入了重力方向的修正和加速度计偏置。
同样地,我们考虑连续的三个连续帧,避免速度计算,并简化表述:
sWpC3=sWpC2+WvB2Δt23−12RWIg^I∧GΔt232δθ+RWB2(Δp23+JΔp23aba)+(RWC2−RWC3)CpB+12RWIg^IGΔt232sWpC2=sWpC1+WvB1Δt12−12RWIg^I∧GΔt122δθ+RWB1(Δp12+JΔp12aba)+(RWC1−RWC2)CpB+12RWIg^IGΔt122WvB2=WvB1+gWΔt12+RWB1(Δv12+JΔv12aba)s_Wp_{C}^{3}=s_Wp_{C}^{2}+_Wv_{B}^{2}\Delta t_{23}-\frac12R_{WI}\hat{g}_I^{\wedge}G\Delta t_{23}^2\delta\theta+R_{WB}^2(\Delta p_{23}+J_{\Delta p23}^ab^a)+(R_{WC}^2-R_{WC}^{3}){_Cp_B}+\frac12R_{WI}\hat{g}_IG\Delta t_{23}^2 \\
s_Wp_{C}^{2}=s_Wp_{C}^{1}+_Wv_{B}^{1}\Delta t_{12}-\frac12R_{WI}\hat{g}_I^{\wedge}G\Delta t_{12}^2\delta\theta+R_{WB}^1(\Delta p_{12}+J_{\Delta p12}^ab^a)+(R_{WC}^1-R_{WC}^{2}){_Cp_B}+\frac12R_{WI}\hat{g}_IG\Delta t_{12}^2 \\
{_Wv_{B}^{2}=_Wv_{B}^{1}+g_W\Delta t_{12}+R_{WB}^1(\Delta v_{12}+J_{\Delta v12}^ab^a)}sWpC3=sWpC2+WvB2Δt23−21RWIg^I∧GΔt232δθ+RWB2(Δp23+JΔp23aba)+(RWC2−RWC3)CpB+21RWIg^IGΔt232sWpC2=sWpC1+WvB1Δt12−21RWIg^I∧GΔt122δθ+RWB1(Δp12+JΔp12aba)+(RWC1−RWC2)CpB+21RWIg^IGΔt122WvB2=WvB1+gWΔt12+RWB1(Δv12+JΔv12aba) 得到
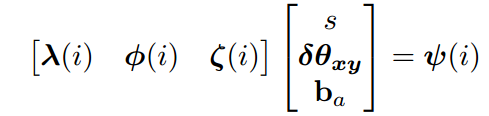
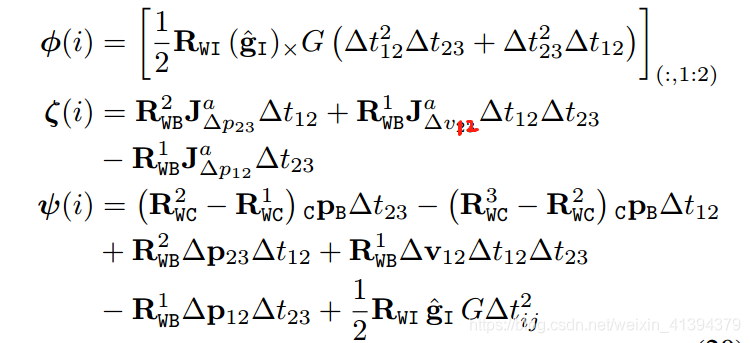
其中,λ(i)\lambda(i)λ(i)为3×1的矩阵,ϕ(i)\phi(i)ϕ(i)为3×2矩阵,ζ(i)\zeta(i)ζ(i)为3×3矩阵,(sδθxyba)\left( \begin{array}{} s\\\delta\theta_{xy}\\b^a \end{array}\right )⎝⎛sδθxyba⎠⎞为6×1矩阵,ψ(i)\psi(i)ψ(i)为3×1矩阵。写成AX=BAX=BAX=B的形式,A3×6,X6×1,B3×1A_{3×6},X_{6×1},B_{3×1}A3×6,X6×1,B3×1,六个未知数,一组关键帧(3帧)有三个方程,所以至少需要两个关键帧组(至少4帧)。若N个关键帧,有N-2组,则A3(N−2)×6,X6×1,B3(N−2)×1A_{3(N-2)×6},X_{6×1},B_{3(N-2)×1}A3(N−2)×6,X6×1,B3(N−2)×1,可以使用最小二乘或SVD求解。
4.估计速度
尺度,重力,陀螺仪、加速度计偏置已知,可以代入原位置关联方程求解速度
sWpCi+1=sWpCi+WvBiΔti,i+1−12RWIg^I∧GΔti,i+12δθ+RWBi(Δpi,i+1+JΔpaba)+(RWCi−RWCi+1)CpB+12RWIg^IGΔti,i+12s_Wp_{C}^{i+1}=s_Wp_{C}^{i}+_Wv_{B}^{i}\Delta t_{i,i+1}-\frac12R_{WI}\hat{g}_I^{\wedge}G\Delta t_{i,i+1}^2\delta\theta+R_{WB}^i(\Delta p_{i,i+1}+J_{\Delta p}^ab^a)+(R_{WC}^i-R_{WC}^{i+1}){_Cp_B}+\frac12R_{WI}\hat{g}_IG\Delta t_{i,i+1}^2sWpCi+1=sWpCi+WvBiΔti,i+1−21RWIg^I∧GΔti,i+12δθ+RWBi(Δpi,i+1+JΔpaba)+(RWCi−RWCi+1)CpB+21RWIg^IGΔti,i+12sWpCi+1=sWpCi+WvBiΔti,i+1+12gWΔti,i+12+RWBiΔpi,i+1+(RWCi−RWCi+1)CpBs_Wp_{C}^{i+1}=s_Wp_{C}^{i}+_Wv_{B}^{i}\Delta t_{i,i+1}+\frac12g_W\Delta t_{i,i+1}^2+R_{WB}^i\Delta p_{i,i+1}+(R_{WC}^i-R_{WC}^{i+1}){_Cp_B}sWpCi+1=sWpCi+WvBiΔti,i+1+21gWΔti,i+12+RWBiΔpi,i+1+(RWCi−RWCi+1)CpB 求解邻近关键帧速度,使用速度关联方程:WvBi+1=WvBi+gWΔti,i+1+RWBi(Δvi,i+1+JΔvgbg+JΔvaba)
_Wv_B^{i+1}=_Wv_B^{i}+g_W\Delta t_{i,i+1}+R_{WB}^{i}(\Delta v_{i,i+1}+J_{\Delta v}^gb^g+J_{\Delta v}^ab^a)WvBi+1=WvBi+gWΔti,i+1+RWBi(Δvi,i+1+JΔvgbg+JΔvaba)
5.重定位后偏置重新初始化
当系统运行一段时间后根据位置辨识重定位,需要对偏置进行重新初始化。陀螺仪偏置仍然是求解最优旋转误差方程,加速度偏置通过求解简化的3中的方程组,其中s和gWg_WgW已知。
























 3070
3070

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








