“The purpose of computation is insight, not numbers."
-Richard Hamming
计算的目的不在于数字本身,而在于洞察其背后的意义。
——理查德·哈明
▼
我们回到最开始的问题—什么是代数?
在大一下学期数学物理方法基础课程的绪论中,兰鹏飞教授为我们介绍了这一背景。
代数的研究对象不仅是数字,⽽是各种抽象化的结构。实际上,数学上重要的并不是对象,⽽是对象间的关系。例如⼏何可以看成是图形的代数,⽽代数也不外是符号的⼏何。故此,代数被定义为对各种集合的元素施⾏代数运算的科学。
因此我们利用几何理解代是逼近代数本质的一种途径。
▼
行列式(determinant)
行列式的定义
什么是行列式?在丘维声《高等代数》中给出了n阶行列式的定义:
定义(n阶行列式)
n阶行列式
是n!项的代数和,其中每一项都是位于不同行、不同列的n个元素的乘积,把这n个元素按照行指标成自然序排好位置,当列指标所成排列是偶排列时,该项带正号;奇排列时,该项带符号,即
其中
是n元排列,
表示对所有n元排列求和。
我认为这个定义更像是生物学中常用的定义法,看完定义我有一种云里雾里的感觉(翻了很多书和课件,大部分书中甚至连定义都没提),对行列式并没有什么更深的认识,只是大概有个印象:它是一堆数排列成矩形,是一个数值。
我们希望做的是把行列式形象化。
▼
线性变换与行列式
在上一篇推文中,我们已经了解了线性变换的几何意义。有的线性变换将空间向外拉伸,有的线性变换将空间向内挤压。由此我们引出一个问题——如何度量一个线性变换将空间拉伸或挤压了多少呢?更具体一点,就是测量一个给定面积(或者是体积,或者是一个表示大小的什么积,这和维度[dimension]有关)增大或缩小的比例。
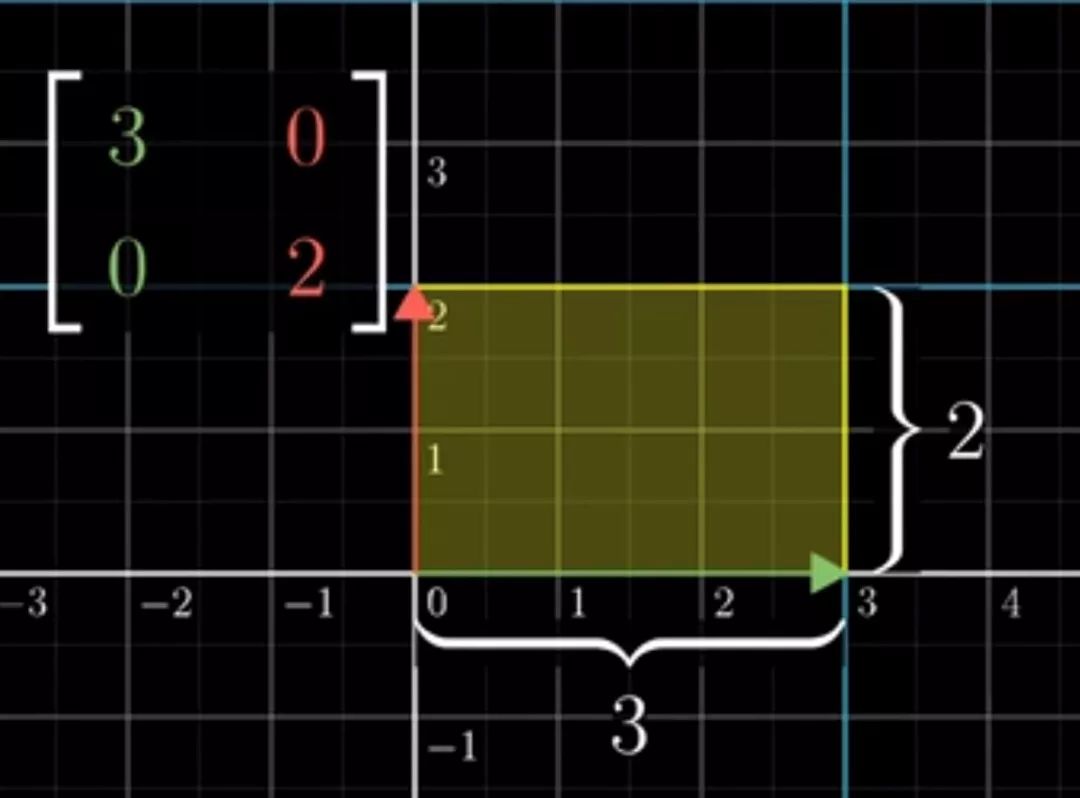
比如说一个矩阵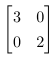 ,将它在坐标系上表示,它在
,将它在坐标系上表示,它在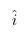 方向上的长度为3,在
方向上的长度为3,在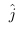 方向上的长度为2,则该矩阵形成的平行四边形面积为3×2=6,即把原来单位矩阵组成的小正方形面积扩大了6倍。
方向上的长度为2,则该矩阵形成的平行四边形面积为3×2=6,即把原来单位矩阵组成的小正方形面积扩大了6倍。
同时我们发现行列式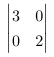 的值就是6啊!!!66666(这并不是偶然,大家用线性变换的方式思考一下行列式就明白了)
的值就是6啊!!!66666(这并不是偶然,大家用线性变换的方式思考一下行列式就明白了)
再来看以下图片上的几个例子(我就不打字了,吐槽一下vx编辑无法使用LaTex只能将公式打好再一个个截图T T)
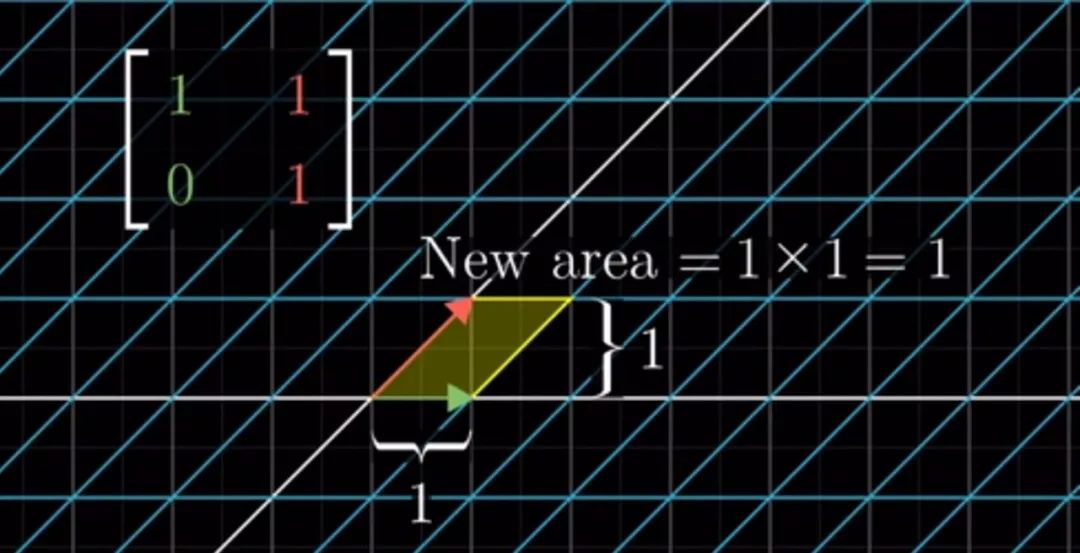



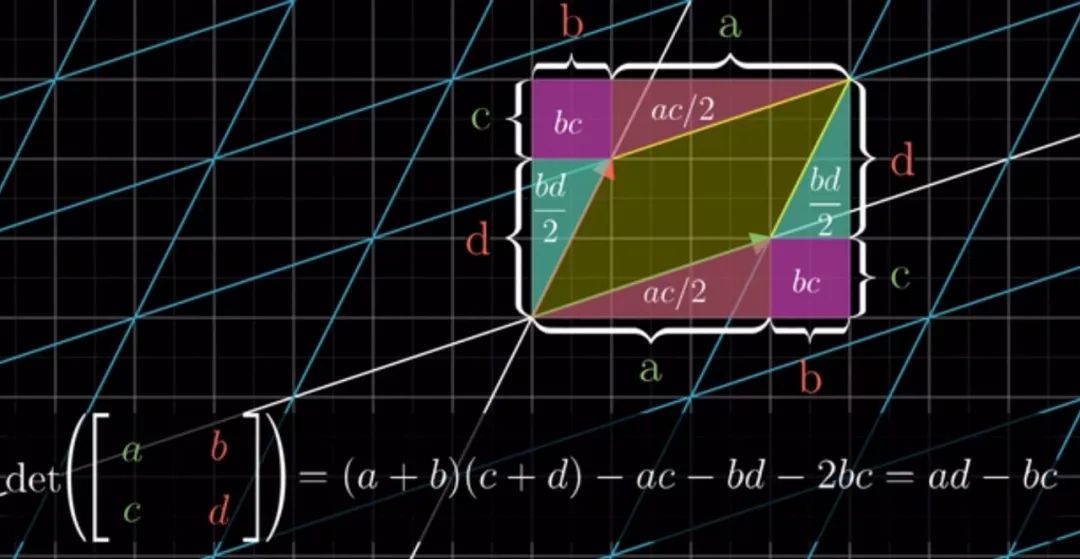
这时候问题又来了,面积是正数,而行列式有正有负有零,这要怎么理解呢?
→ 变换之前,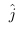 在
在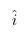 的左侧,若行列式的值为负,则变换后
的左侧,若行列式的值为负,则变换后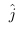 在
在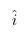 的右侧,可以想象成,把二维坐标翻转了(简单地说,就是把纸翻过来了)
的右侧,可以想象成,把二维坐标翻转了(简单地说,就是把纸翻过来了)
让我们来重新定义行列式:
线性变换改变面积的比例,称为这个变换的行列式。
这是二维/二阶行列式(两个并不等价,只是这样写方便理解)的情况。那么在三维空间中呢?
在三维空间中,行列式代表平行六面体的体积,而加负号则代表从坐标系从右手系转换到左手系。
同样推广到更n阶行列式,行列式代表n维空间的大小,而负号代表n维空间的翻转。
行列式的值等于0又代表什么呢?
以三阶行列式为例,它代表三维空间被压缩成一个平面,甚至压缩成一个点。这时我们说,行列式的行(row)或列(column)是线性相关的。这也很好解释我们在后面学到的:数域K上n级矩阵A可逆的充分必要条件是|A|≠0
感谢阅读 欢迎指正
下一篇文章将是关于特殊矩阵探究的一篇小论文,将提出关于n阶单位三角矩阵m次幂的通式。推导来自Linear Algebra阅读小组的组员们的共同探讨。







 本文探讨了行列式的几何意义,从代数结构出发,解释了行列式如何反映线性变换对空间的拉伸和挤压比例。在二维空间中,行列式为正表示保持方向,负表示翻转,为0则意味着线性相关。在高维空间,行列式为0意味着空间被压缩至更低维。通过这个概念,我们能更好地理解协方差矩阵行列式为0的含义。
本文探讨了行列式的几何意义,从代数结构出发,解释了行列式如何反映线性变换对空间的拉伸和挤压比例。在二维空间中,行列式为正表示保持方向,负表示翻转,为0则意味着线性相关。在高维空间,行列式为0意味着空间被压缩至更低维。通过这个概念,我们能更好地理解协方差矩阵行列式为0的含义。

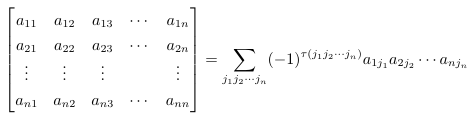
















 1051
1051

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








