特征归一化/标准化/BN/LN/RMS-norm/key-norm/Query-Norm？

zhurui_xiaozhuzaizai

已于 2025-03-17 16:37:54 修改

阅读量707

点赞数

分类专栏：机器学习文章标签：算法自然语言处理

于 2021-04-08 11:59:22 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_36378508/article/details/115514628

版权

机器学习专栏收录该内容

35 篇文章

订阅专栏

一：标准化和归一化

1.1 定义和概念

无量纲化使不同规格的数据转换到同一规格。常见的无量纲化方法有标准化和区间缩放法。

标准化的前提是特征值服从正态分布，标准化后，其转换成标准正态分布。
区间缩放法利用了边界值信息，将特征的取值区间缩放到某个特点的范围，例如[0, 1]等。

标准化（Standardization）和 **归一化（Normalization）**是数据预处理中常用的两种技术，目的是调整数据的尺度，使得不同特征的数据可以在同一水平上进行比较或处理。这两种方法在形式和用途上有所不同

标准化是依照特征矩阵的列处理数据，其通过求z-score的方法，将样本的特征值转换到同一量纲下。
归一化是依照特征矩阵的行处理数据，其目的在于样本向量在点乘运算或其他核函数计算相似性时，拥有统一的标准，也就是说都转化为“单位向量”

1.2 为什么归一化

为什么要做特征归一化
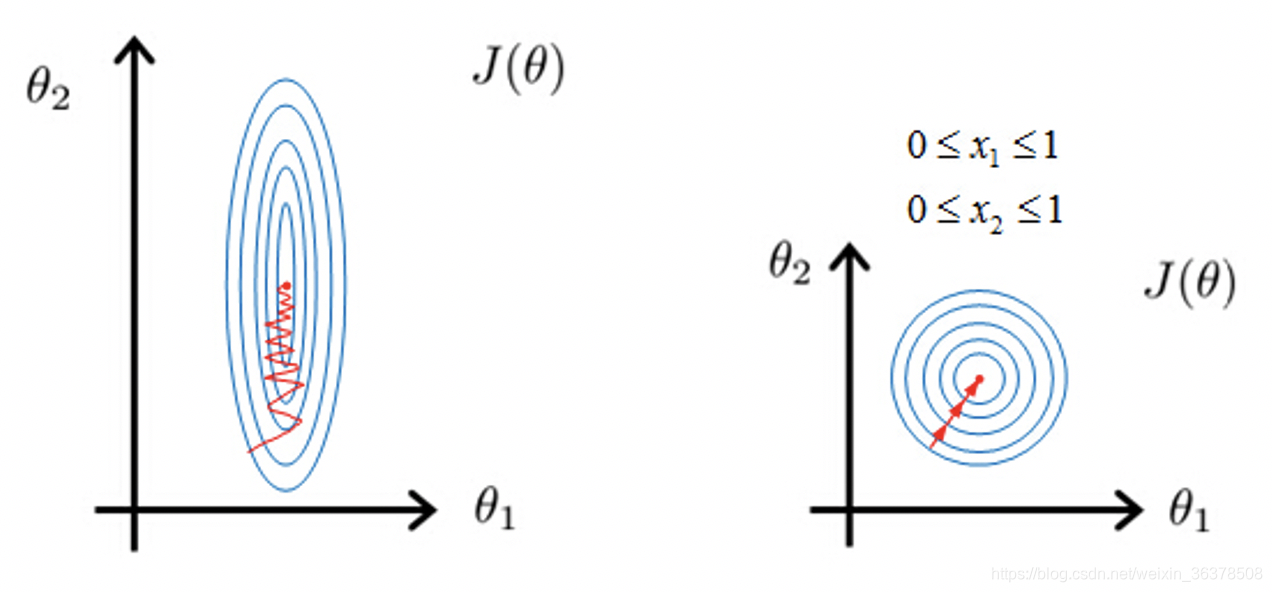
在采用梯度更新的学习方法（包括线性回归，逻辑回归，支持向量机，神经网络）等求解过程中。为归一化参数在学习时，梯度下降较为抖动，模型难以收敛，而归一化可以使梯度下降较为稳定，进而减小梯度下降的次数，模型也能很快收敛。

二：归一化方法

在这里插入图片描述

BatchNorm (2015)：通过批次维度统计量进行标准化，解决了深层网络训练中的梯度问题。BatchNorm 是在 batch 维度上进行归一化，针对的是中间层的单个神经元。对于每个 mini-batch，计算该神经元的均值和方差，然后对该 mini-batch 中的所有样本进行归一化。

LayerNorm (2016)：LayerNorm 是在 layer 维度上进行归一化，针对的是中间层的单个样本。对于每个样本，计算该层所有神经元的均值和方差，然后对该层的所有神经元进行归一化。更适合处理序列数据。

RMSNorm (2019)：RMSNorm 可以看作是 LayerNorm 的简化版本，它只使用均方根 (Root Mean Square, RMS) 进行归一化，省略了减去均值的步骤。被LLaMA等大模型采用。

在这里插入图片描述

2.1 BN

BN的理解
BN就是为了解决偏移的，解决的方式也很简单，就是让每一层的分布都normalize到标准高斯分布。（BN是根据划分数据的集合去做Normalization，不同的划分方式也就出现了不同的Normalization，如GN，LN，IN）
[N, H, W, C]，其中N是batch_size，H、W是行、列，C是通道数，BN是对NHW进行归一化；对batch中对应的channel归一化

LN避开了batch维度，归一化的维度为[C，H，W]。
IN 归一化的维度为[H，W]；
GN介于LN和IN之间，其首先将channel分为许多组（group），对每一组做归一化，及先将feature的维度由[N, C, H, W]reshape为[N*G，C//G , H, W]，归一化的维度为[C//G , H, W]

训练和推理式君之和方差分别是多少
训练时：均值、方差分别是该批次内数据相应维度的均值与方差。
推理时：均值来说直接计算所有训练时batch的的平均值，而方差采用训练时每个batch的的无偏估计；但在实际实现中，如果训练几百万个Batch，那么是不是要将其均值方差全部储存，最后推理时再计算他们的均值作为推理时的均值和方差？这样显然太过笨拙，占用内存随着训练次数不断上升。为了避免该问题，后面代码实现部分使用了滑动平均，储存固定个数Batch的均值和方差，不断迭代更新推理时需要的均值和方差

BN好处
防止网络梯度消失：这个要结合sigmoid函数进行理解
加速训练，也允许更大的学习率：数据在一个合适的分布空间，经过激活函数，仍然得到不错的梯度。梯度好了自然加速训练。
降低参数初始化敏感
提高网络泛化能力防止过拟合：
可以把训练数据彻底打乱

key-norm与外推性

2.2 LN

2.3 RMS norm

2.4 DYT

2.4.1 LayerNorm的输入-输出映射呈现出类tanh的S型曲线+

LayerNorm并非严格意义上的线性变换,其输入-输出映射呈现出类tanh的S型曲线。
这种非线性特性并非设计初衷,而是训练过程中自然形成的–由每个token的标准化过程独立,以及不同token的统计量差异导致的。
S型曲线可以缓解梯度消失/爆炸问题,提高泛化能力,但也可能损失一些信息,增加训练难度。

从单个神经元的角度来看,LayerNorm是一个线性变换。

但是,从整个layer的角度来看,LayerNorm并不是一个线性变换。因为每个神经元的均值μ和方
差o2都是由该layer的所有神经元共同决定的。也就是说,不同神经元的LayerNorm 变换是相互
影响的。

2.4.2 S型曲线的产生,主要是由于以下两个原因:

每个token的标准化过程独立:Transformer中的每个token都是独立进行LayerNorm的,这意
味着不同token的统计量(均值和方差)可能不同。
不同token的统计量差异导致整体非线性:由于不同token的的统计量不同,因此它们的
LayerNorm 变换也不同。当我们将所有token的输入-输出映射放在一起观察时,就会发现整体呈
现出S型曲线。

我们可以用一个简单的例子来说明。
假设有两个token,它们的输入分别为x1和x2,
它们的均值μ1,μ2和方差分别为从σ1²和u2²。则它们的LayerNorm输出分别为:
由于μ1不等于μ2, σ1²不等于u2²,因此LayerNorm(x1)和LayerNorm(x2)的变换也不同。
当我们将x1和LayerNorm(x1),x2和LayerNorm(x2)的关系绘制在同一个图上时,就会发现整体呈现出S型曲线。

2.4.3 深层网络中的特征分布双极分化

深层网络中的特征分布双极分化,指的是在深层网络中,一些神经元的输出会变得非常大,而另一
些神经元的输出会变得非常小。这种现象会导致梯度消失夫或爆炸,影响网络的训练。

这主要是由于深层网络的复合效应。在深层网络中,每一层的输出都会受到前面所有层的影响。如
果前面的层出现了一些异常值,这些异常值会被逐层放大大,最终导致某些神经元的输出变得非常
大。
LayerNorm的S型曲线可以缓解这种双极分化。因为S型曲钱可以将极端值压缩到一个较小的范
围内,从而防止这些极端值被逐层放大。

2.4.4 非线性特性的影响

LayerNorm的非线性特性对Transformer的影响是复杂的,既有好处也有坏处。
好处:
缓解梯度消失/爆炸:S型曲线可以压缩极端值,从而缓解梯度消失/爆炸问题。
提高泛化能力:S型曲线可以防止网络过于依赖于训练数据,从人而提高泛化能力。
坏处:
可能损失信息:S型曲线的非线性压缩可能会损失一些信息。
增加训练难度:非线性变换会增加训练的难度。

2.4.5 tanh替代layerNorm

2.4.6 有哪些不足和弊端

为什么在CNN中效果不佳?

ResNet-50+替换BN后精度下降,可能得原因在于:
架构差异:CNN的卷积层输出空间相关性强,同一通道内不同位置统计量差异大,需要BN的局部归一化。
频率问题:BN在CNN中每层都有,而Transformer中LayerNormi间隔多个自注意力层,DyT的全局缩放难以适应高频统计变化。
初始化耦合:CNN通常依赖BN的初始化特性(如零初始化bias),直接替换破坏初始化平衡。可尝试结合通道注意力(如SE模块+),为每个通道学习独立的α,但会增加参数量。

DyT的「动态」本质是否被高估?

论文强调DyT通过可学习参数α实现动态缩放,但实验显示α最终与与输入标准差倒数(1/σ)高度相
关。这暗示DyT可能只是将显式的统计量计算(LayerNorm的σ)转化为隐式的参数学习,并未真正
摆脱归一化的统计逻辑。
α的学习目标与LayerNorm的1/σ相似,但关键差异在于计算方式。LayerNorm动态计算每个token的
σ,而DyT通过全局学习一个固定α,牺牲了细粒度统计适应性,接换取了计算效率
LayerNorm的归一化是「数据依赖型」(data-dependent),随输入实时变化;DyT是「参数依赖
型」(parameter-dependent),通过训练集整体统计调整α。这可可能导致DyT在分布偏移(OOD)
场景下表现更差(论文未验证)。

DyT在LLM中需分层调整α可能引发「级联敏感性问题」

LLaMA实验显示,模型宽度越大,α需越小,且注意力模块需更高α。这表明DyT对网络深度和模块
类型敏感,可能因参数耦合引发级联误差。
深层Transformer中,激活的幅度会随深度指数増长或衰减,这要求每层的α具备自适应调节能力。
然而,DyT的α是独立学习的,缺乏跨层协同机制。
对比LayerNorm,LN通过逐token计算σ,天然适应不同层的幅度变化,而DyT的固定α需通过训练
被动调整,导致深层网络需要精细初始化(如LLaMA的分层α)。
这可能说明,效率提升(固定α)与动态适应性(LayerNorm的实时计算)难以兼得。DyT在LLM中
的成功依赖大量试错调参(如表12的网格搜索),实用性存疑。

在这里插入图片描述

特征归一化方法
是将原本特征都统一到一个大致的区间。例如【0，1】，常用归一化方法有：
min-max-scaling:[0,1]等比例缩放

z-score noemalization，映射到均值为0，标准差为1的分布上

数据预处理
2.1 无量纲化
　 2.1.1 标准化
　　　　2.1.2 区间缩放法
　　　　2.1.3 标准化与归一化的区别
　　2.2 对定量特征二值化
　　2.3 对定性特征哑编码
　　2.4 缺失值计算
　　2.5 数据变换

二 BN

树形特征为什么不需要归一化
因为数值缩放不影响分裂点位置，对树模型的结构不造成影响。

按照特征值进行排序的，排序的顺序不变，那么所属的分支以及分裂点就不会有不同。

而且，树模型是不能进行梯度下降的，因为构建树模型（回归树）寻找最优点时是通过寻找最优分裂点完成的，因此树模型是阶跃的，阶跃点是不可导的，并且求导没意义，也就不需要归一化。