对抗训练基本思想——Min-Max公式
中括号里的含义为我们要找到一组在样本空间内、使Loss最大的的对抗样本(该对抗样本由原样本x和经过某种手段得到的扰动项r_adv共同组合得到)。这样一组样本组成的对抗样本集,它们所体现出的数据分布,就是该中括号中所体现的。
外层min()函数指的则是,我们面对这种数据分布的样本集,要通过对模型参数的更新,使模型在该对抗样本集上的期望loss最小
对抗训练的核心步骤是:
用被对抗性样本污染过的训练样本来训练模型,直到模型能学习到如此类型的抵抗。从而保证模型的安全性,在自动驾驶和图像识别领域,保证模型的安全性尤为重要。
如何找到最佳扰动r_adv呢?
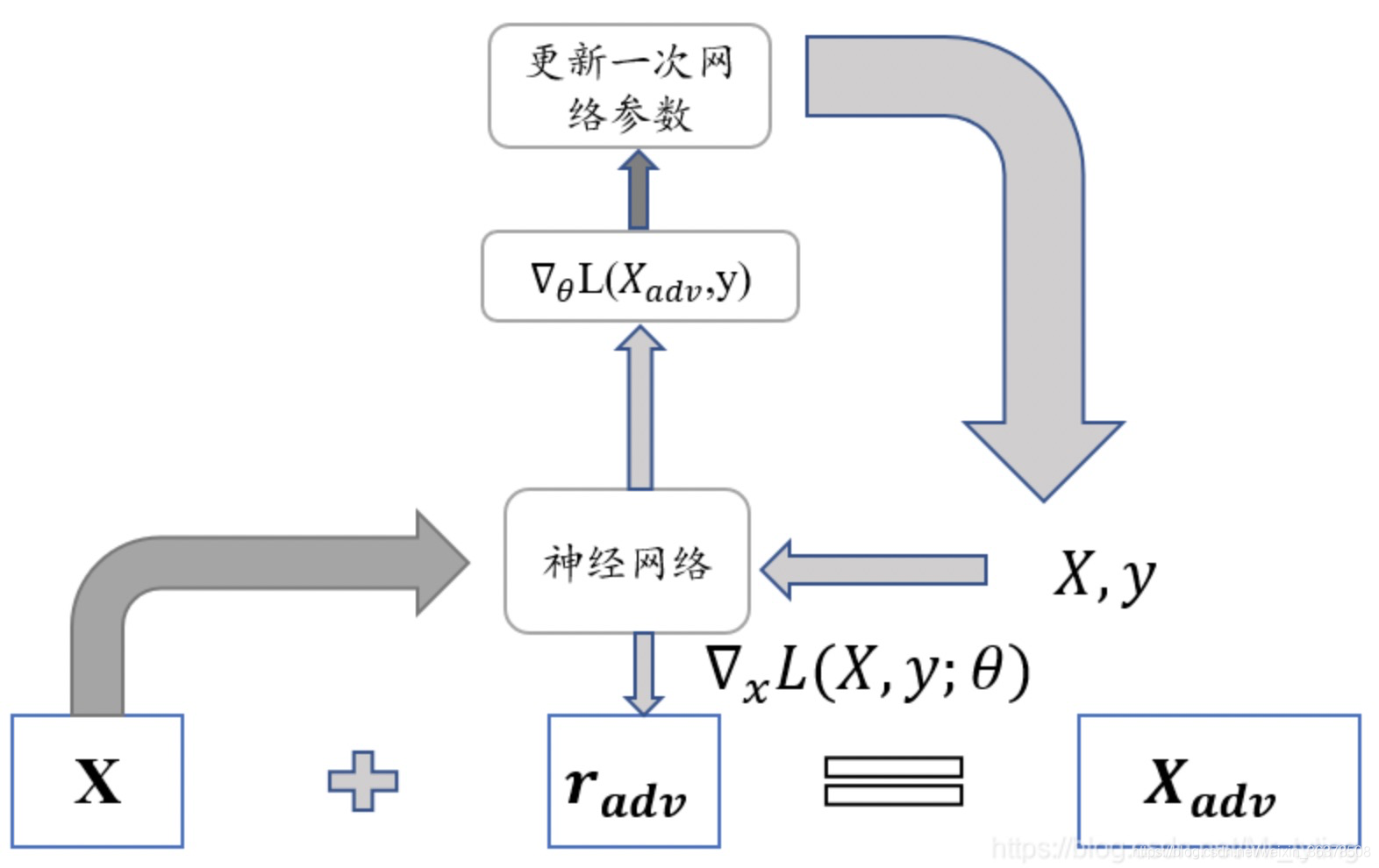
很简单——梯度上升。所以说,对抗训练本质上来说,在一个step中,实际上进行了两次梯度更新,只不过是被更新的对象是不同的——首先先做梯度上升,找到最佳扰动r,使得loss最大;
其次梯度下降,找到最佳模型参数(所有层的模型参数,这一步和正常模型更新、梯度下降无异),使loss最小。 具体情况如图所示:
注:所谓“attack”,即:
它是谁:attack就是将已算出的扰动加到embedding上的操作;
它从哪来(定位在哪):attack操作是在梯度上升使loss最大、求best扰动r的过程中进行的,它的目的就是看看怎么attack才能得到最佳扰动;
它要干啥(作用):对word-embedding层attack后,计算“被attack后的loss”,即对抗loss(adv_loss),然后据此做梯度上升,对attack的扰动r进行梯度更新。
对抗学习已经在图像领域取得了不错的效果,可否将这种方式对抗训练迁移到NLP上呢?因为NLP中的输入raw_text是离散的,无法直接在raw_text上加上扰动,Goodfellow在17年提出了可以在连续的embedding上做扰动,但这样做有一个问题,训练模式时可以这样加入扰动(已知label,喂给模型是扰动后的训练样本),在模型预测时,如何加入扰动呢?(label未知,喂给模型的是正常训练样本),通常在图像领域,经过对抗训练后的模型在正常样本上表现很差,而在NLP中,由大量实验表明,对抗学习后的模型泛化能力变强了。因此在NLP任务中,对抗训练的目的不再是为了防御基于梯度的恶意攻击,反而更多的是作为一种regularization,提高模型的泛化能力。因此论文中也提到:We turn our focus away from the security benefits of adversarial training, and instead study its effects on generalization.
常见的几种对抗训练算法
FGSM (Fast Gradient Sign Method): ICLR2015
FGSM是Goodfellow提出对抗训练时的方法,假设对于输入的梯度为:
那扰动肯定是沿着梯度的方向往损失函数的极大值走:
Fast Gradient Method(FGM)ICLR2017
FSGM是每个方向上都走相同的一步,Goodfellow后续提出的FGM则是根据具体的梯度进行scale,得到更好的对抗样本:
1 一切照常,计算前向loss,然后反向传播计算grad(注意这里不要更新梯度,即没有optimizer.step())
2 拿到embedding层的梯度,计算其norm,然后根据公式计算出r_adv,再将r_adv累加到原始embedding的样本上,即 x+r
3 得到对抗样本; 根据新对抗样本 x+r, 计算新loss,在backward()得到对抗样本的梯度。由于是在step(1)之后又做了一次反向传播,所以该对抗样本的梯度是累加在原始样本的梯度上的;
4 将被修改的embedding恢复到原始状态(没加上r_adv 的时候);
5 使用step(3)的梯度(原始梯度+对抗梯度),对模型参数进行更新(optimizer.step()/scheduler.step()).
FGM的官方实现
class FGM():
def __init__(self, model):
self.model = model
self.backup = {
}
def attack(self, epsilon=1., emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {
}
# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
由代码可知,相当于做一次对抗训练更新一次网络参数。并且每次都是在原始的embedding空间上加扰动,而非在上一次加扰动的基础上再加扰动。
Projected Gradient Descent(PGD)ICLR2018
FGM直接通过epsilon参数一下子算出了对抗扰动,这样得到的可能不是最优的。因此PGD进行了改进,多迭代几次,慢慢找到最优的扰动。
FGM简单粗暴的“一步到位”,可能走不到约束内的最优点。PGD则是“小步走,多走几步”,如果走出了扰动半径为epsilon的空间,就映射回“球面”上,以保证扰动不要过大
由上面公式(1)(2)可以看出,在一步更新网络内(公式2),在S 范围内进行了多步小的对抗训练(公式1),在这多步小的对抗训练中,对wordEmbe





 本文深入解析了对抗训练的基本思想及其在NLP领域的应用,包括FGSM、FGM、PGD等多种算法,并介绍了FreeAT、YOPO、FreeLB等优化方法。
本文深入解析了对抗训练的基本思想及其在NLP领域的应用,包括FGSM、FGM、PGD等多种算法,并介绍了FreeAT、YOPO、FreeLB等优化方法。


![[公式]](https://i-blog.csdnimg.cn/blog_migrate/3dca44b9050fc740c15c7257d1b81328.png)
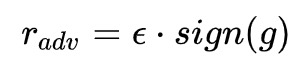
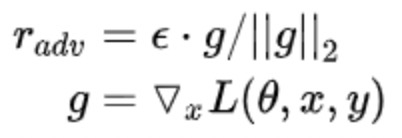
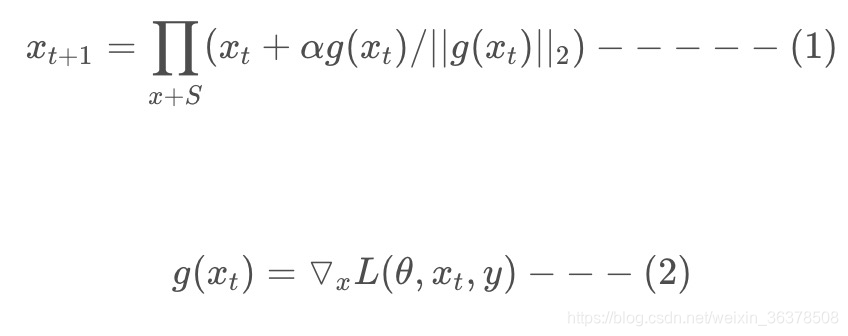
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 955
955










