UE4中的Material Parameter Collection

Material Parameter Collection的含义

直译过来就是材质参数集合。这个东西在材质中可以当做参数使用。

创建Material Parameter Collection

在ContentBrowser的空白处右键：

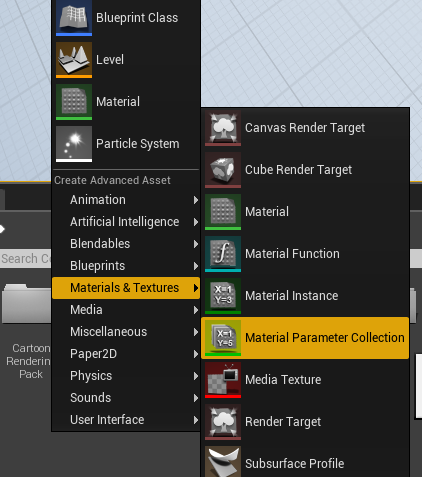
这样就创建了材质参数集合。

双击打开之后，可以添加参数。

在材质中使用Material Parameter Collection

材质中的参数，一般长这个样子：

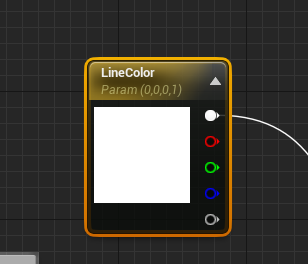
这个参数可以在编辑器中设置，也可以在运行时设置。

材质中还有一种参数，是这么创建的：

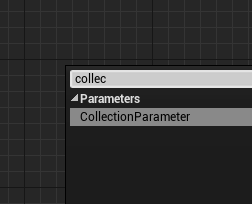
创建之后长这个模样：

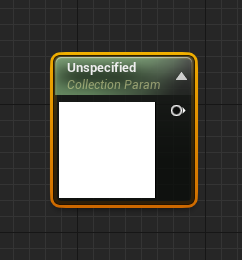
选中这个节点，可以选择一些属性。

在Collection这个属性，点一下下拉菜单：

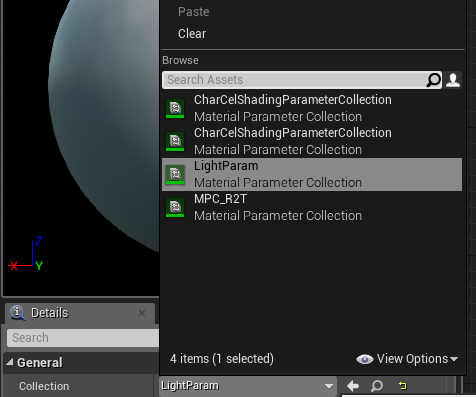
这里出现的，就是Material Parameter Collection了。

我这里选择LightParam，这个参数集合是我创建的。

然后接着选择ParameterName，里面是LightParam这个集合中的参数。

下面是选了之后的样子：

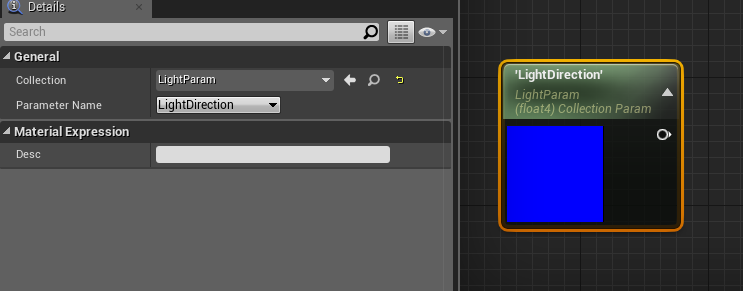
这样，材质中这个参数的值，就是LightParam的LightDirection了。

Material Parameter Collection的机制

当在蓝图中修改LightDirection的时候，材质中这个参数的值也跟着同时变化。

这是在蓝图中修改材质参数集合的蓝图节点：

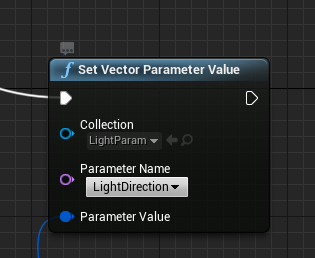
可以看到，材质参数集合，其实就是全局变量。

 

转载于:https://www.cnblogs.com/henzhe/p/9556074.html