hdu 4421 Bit Magic

最新推荐文章于 2025-04-14 22:26:17 发布

weixin_30834019

最新推荐文章于 2025-04-14 22:26:17 发布

阅读量111

点赞数

原文链接：http://www.cnblogs.com/wuminye/p/3274609.html

版权

【题意】

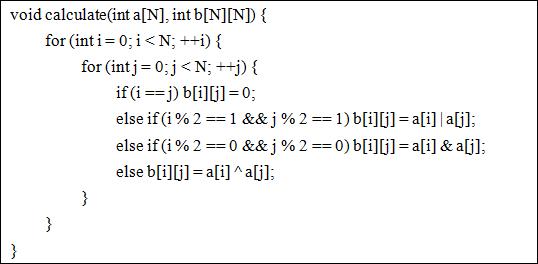
这个函数是给A求B的，现在给你B，问你是否能有A的解存在。

【2-SAT解法】

对于每个A[i]的每一位运行2-sat算法，只要跑到强连通就可以结束，应为只要判断是否有解，后面拓扑求解就不需要了。构图和算法思想和基本的2-sat一致，详见我的2-sat博文。

  1 #include <stdio.h>
  2 #include <string.h>
  3 inline int min(int a,int b){return a>b?b:a;}
  4 struct edge
  5 {
  6     int v,next;
  7     edge(int d=0,int n=-1):v(d),next(n){}
  8     void set(int d,int n){v=d;next=n;}
  9 }data[500*2001];
 10 int head[1024],hn;
 11 void adde(int a,int b)
 12 {
 13     data[hn].set(b,head[a]);
 14     head[a]=hn++;
 15 }
 16 int n;
 17 int b[501][501];
 18 int dfn[1024],low[1024],sta[1024],belong[1024];
 19 bool ifin[1024];
 20 int top,group,dep;
 21 void tarjan(int u)
 22 {
 23     dfn[u]=low[u]=++dep;
 24     sta[++top]=u;
 25     ifin[u]=true;
 26     for (int i=head[u];i!=-1;i=data[i].next)
 27     {
 28         int v=data[i].v;
 29         if (!dfn[v])
 30         {
 31             tarjan(v);
 32             low[u]=min(low[u],low[v]);
 33         } else
 34         {
 35             if (ifin[v]) low[u]=min(low[u],dfn[v]);
 36         }
 37     }
 38     if (dfn[u]==low[u])
 39     {
 40         int j;
 41         ++group;
 42         do
 43         {
 44             j=sta[top--];
 45             belong[j]=group;
 46             ifin[j]=false;
 47         } while (u!=j);
 48     }
 49 }
 50 void init()
 51 {
 52     hn=dep=group=0;
 53     top=-1;
 54     memset(head,-1,sizeof head);
 55     memset(dfn,0,sizeof dfn);
 56     memset(ifin,false,sizeof ifin);
 57 }
 58 bool judge()
 59 {
 60     for (int i=0;i<n;++i)
 61         if (belong[i]==belong[i+n]) return false;
 62     return true;
 63 }
 64 bool solve()
 65 {
 66     for (int i=0;i<n;++i)
 67         for (int j=i;j<n;++j)
 68     {
 69         if (i==j && b[i][j]) return false;
 70         if (b[i][j]!=b[j][i]) return false;
 71     }
 72     for (int k=0;k<31;++k)
 73     {
 74         init();
 75         for (int i=0;i<n;++i)
 76             for (int j=i;j<n;++j)
 77         {
 78             int m=b[i][j]&(1<<k);
 79             if (i==j) continue;
 80             if (i&1 && j&1) // |
 81             {
 82                 if (m)
 83                 {
 84                     adde(i,j+n);
 85                     adde(j,i+n);
 86                 } else
 87                 {
 88                     adde(i+n,i);
 89                     adde(j+n,j);
 90                 }
 91             } else if (!(i&1) && !(j&1)) //&
 92             {
 93                 if (m)
 94                 {
 95                     adde(i,i+n);
 96                     adde(j,j+n);
 97                 } else
 98                 {
 99                     adde(i+n,j);
100                     adde(j+n,i);
101                 }
102             } else   // ^
103             {
104                 if (m)
105                 {
106                     adde(i,j+n);
107                     adde(j,i+n);
108                     adde(j+n,i);
109                     adde(i+n,j);
110                 } else  //==
111                 {
112                     adde(i,j);
113                     adde(j,i);
114                     adde(i+n,j+n);
115                     adde(j+n,i+n);
116                 }
117             }
118         }
119         for (int i=0;i<(n<<1);++i)
120             if (!dfn[i]) tarjan(i);
121         if (!judge()) return false;
122     }
123     return true;
124 }
125 int main()
126 {
127     while (~scanf("%d",&n))
128     {
129         for (int i=0;i<n;++i)
130             for (int j=0;j<n;++j)
131               scanf("%d",&b[i][j]);
132         if (solve()) puts("YES"); else puts("NO");
133     }
134 }

2-sat

【并查集】

主要思想是以A中每个元素的每一位作为一个基本单位，根据b中的值来确定每一位之间的等价关系，值相等的并在一个集合，每当能确定一个新的关系时验证原先的关系是否矛盾。不过在处理的时候有点小技巧，与2-sat的思想类似，扩充成2N个点，对于每一位，有个点代表其值，另一点代表其值的反。能确定一位的值时要同时更新这2点，从一方面说是充分发掘信息，另一方面说是为了异或运算的判断服务，因为异或不能确定一个值，但能确定相对关系，需要用到反。

并查集的算法在这题里比2-SAT的快，剩了些不必要的计算，思想也挺巧妙的。

  1 #include <stdio.h>
  2 #include <string.h>
  3 #define N  501*32
  4 #define m1 mset.find(1)
  5 #define m0 mset.find(0)
  6 struct myset
  7 {
  8     int uset[501*64+10];
  9     myset(){init();};
 10     void init(){memset(uset,-1,sizeof uset);}
 11     int find(int k)
 12     {
 13         if (uset[k]==-1) return k;
 14         return uset[k]=find(uset[k]);
 15     }
 16     void uion(int a,int b)
 17     {
 18         int aa=find(a);
 19         int bb=find(b);
 20         if (aa==bb) return;
 21         uset[aa]=bb;
 22     }
 23 }mset;
 24 int b[501][501],n;
 25 bool solve()
 26 {
 27     for (int i=0;i<n;++i)
 28         for (int j=i;j<n;++j)
 29     {
 30         if (i==j && b[i][j]) return false;
 31         if (b[i][j]!=b[j][i]) return false;
 32     }
 33     for (int i=0;i<n;++i)
 34         for (int j=0;j<n;++j)
 35     {
 36         if (i==j) continue;
 37         if (i&1 && j&1)
 38         {
 39             for (int k=0;k<32;++k)
 40             {
 41                 if (b[i][j]&(1<<k) == 0)
 42                 {
 43                     int p1=i*32+k+2;
 44                     int p2=j*32+k+2;
 45                     if (mset.find(p1)==m1 || mset.find(p2)==m1 || mset.find(p1)==mset.find(p2+N)) return false;
 46                     mset.uion(p1,0);
 47                     mset.uion(p2,0);
 48                     mset.uion(p1+N,1);
 49                     mset.uion(p2+N,1);
 50                 }
 51             }
 52         } else
 53         if (!(i&1) && !(j&1))
 54         {
 55             for (int k=0;k<32;++k)
 56             {
 57                  if (b[i][j]&(1<<k))
 58                 {
 59                     int p1=i*32+k+2;
 60                     int p2=j*32+k+2;
 61                     if (mset.find(p1)==m0 || mset.find(p2)==m0 || mset.find(p1)==mset.find(p2+N)) return false;
 62                     mset.uion(p1,1);
 63                     mset.uion(p2,1);
 64                     mset.uion(p1+N,0);
 65                     mset.uion(p2+N,0);
 66                 }
 67             }
 68         } else
 69         {
 70              for (int k=0;k<32;++k)
 71             {
 72                   int p1=i*32+k+2;
 73                   int p2=j*32+k+2;
 74                  if (b[i][j]&(1<<k))
 75                 {
 76                     if (mset.find(p1)==mset.find(p2)) return false;
 77                     mset.uion(p1,p2+N);
 78                     mset.uion(p2,p1+N);
 79                 } else
 80                 {
 81                     if (mset.find(p1)==mset.find(p2+N) ) return false;
 82                     mset.uion(p1,p2);
 83                     mset.uion(p1+N,p2+N);
 84                 }
 85             }
 86         }
 87     }
 88     return true;
 89 }
 90 int main()
 91 {
 92     while (~scanf("%d",&n))
 93     {
 94         mset.init();
 95         for (int i=0;i<n;++i)
 96             for (int j=0;j<n;++j)
 97             scanf("%d",&b[i][j]);
 98         if (solve()) puts("YES"); else puts("NO");
 99     }
100 }