Chapter13 带有多元协变量的函数型因变量回归模型
(以下内容来自 Ramsay and Silverman 的 Functional Data Analysis ;second edition的翻译,初次写博客和翻译英文,有很多不足之处,请大家批评指正!)
13.1 引言
13.2 预测不同气候带的温度曲线
13.2.1 拟合模型
13.2.2 评估拟合效果
13.3 force plate data for walking horses
本节主要描述了关于马步态的有趣数据,数据由布里斯托尔大学马运动医学中心的艾伦·威尔逊博士及其合作者收集。感谢他们允许使用这些数据。这些数据为讨论我们的函数线性建模和方差分析方法的各种扩展提供了机会。有关此示例的更多详细信息,请参阅Wilson等人(1996)。
13.3.1 数据结构
数据的基本结构如下。研究不同类型的马蹄铁和不同的行走表面对马步态的影响是很有意义的。其中一个原因是简单的生物力学:马是一种非常适合步行和跑步的动物,对其步态的研究具有内在的科学兴趣。第二,如果马匹跛足或可能跛足,允许它们比赛是危险的。仔细研究他们的步态可能会产生早期跛行的诊断测试,这些测试不涉及任何侵入性的研究,并且可能会在很早的阶段,在他们变得严重或永久之前检测到损伤。第三,马蹄平衡步态是非常重要的,要做到这一点,必须了解不同类型的马蹄铁的效果。事实上,一旦知道了马的正常步态,我们所描述的测量值就可以用来测试铁匠是否正确地给马蹄钉铁了,因此可以作为训练蹄铁工的辅助手段。
在这项实验中,马走到一块约1平方米的木板上,木板放在地上,在每个角落配备测量垂直和两个水平方向力的仪表。我们只考垂直力。在马蹄在地面(站姿阶段)期间,四个测量的垂直力允许仪器测量产生垂直合力的点。在站立阶段马蹄本身不会移动,马蹄的位置是通过用锯末在板上撒上灰尘来测量的,或者是在只有蹄的前端与地面接触的情况下,从步幅末端的力点推断出来的。
垂直力在标准相位开始时增长很快,但在结束时降低得更慢。在操作上,站姿阶段被定义为从总垂直力第一次达到其最大值的30%开始,到其最大值的8%结束。对于每一次重复,将计算100个时间点的力点,这些时间点在这个时间间隔内等距分布。
因此在站立阶段,一个典型的关于时间的二维函数型观测值
f
o
r
c
e
=
(
f
o
r
c
e
X
,
f
o
r
c
e
Y
)
force=(forceX,forceY)
force=(forceX,forceY),
t
t
t的变化是从0到1。在t时刻,force的坐标为
f
o
r
c
e
X
(
t
)
forceX(t)
forceX(t)和
f
o
r
c
e
Y
(
t
)
forceY(t)
forceY(t),
Y
Y
Y是马的运动方向,
X
X
X是测量垂直于马身方向的距离。因此,如果测量左脚,则坐标的定义就好像是从上方看板一样,如果测量右脚,则坐标定义为X方向的反映。
数据集包括592次单独的跑步,包括8匹马,每匹马的右前肢和左前肢都有许多测量值。九种马蹄铁的情况如下:首先,观察马蹄未钉铁的情况;然后再观察马蹄钉铁的情况;然后,通过添加各种楔子对马蹄铁进行调整,或是脚趾或脚后跟,或是蹄的一边或另一边。并不是所有的马都用楔子。对于脚趾和脚跟加楔子,在楔子固定后立即观察马的运动,一天后,在马习惯于马蹄铁后观察马的运动。最后,取下楔子,用一只正常的马蹄铁观察马匹。
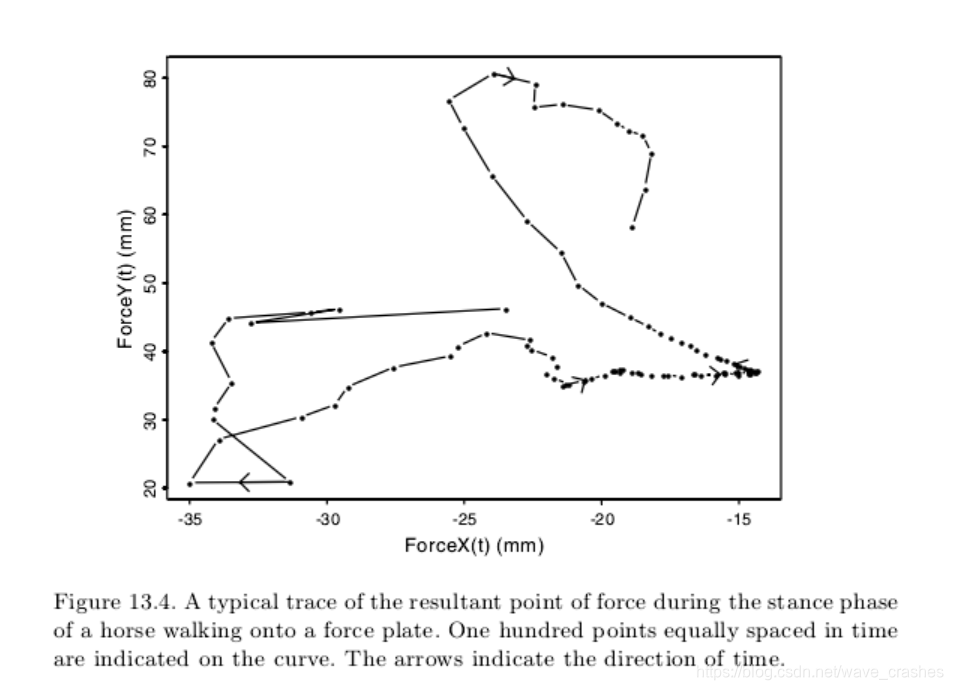
图13.4显示了典型(forcex,forcey)图。这种实现是在获得的平滑曲线中进行的。在曲线上标出时间间隔相等的100个点,并用箭头指示时间方向(也就是时间间隔相等)。毫不奇怪,我们可以看到力的点在接近站姿阶段的开始和结束时移动得最快。一个点的测量精度在每个方向上约为1毫米。
13.3.2 horse data 的函数型线性模型
本实验的主要目的是为了研究不同的马蹄铁的影响,特别是研究脚趾和脚跟楔子的影响,并且这种影响随着马习惯楔子而变化。我们拟合了以下模型形式:
f
o
r
c
e
i
j
k
l
=
μ
+
α
i
j
+
θ
k
+
ϵ
i
j
k
l
force_{ijkl}=\mu+\alpha_{ij}+\theta_k+\epsilon_{ijkl}
forceijkl=μ+αij+θk+ϵijkl
上式中的所有项都是关于t的二维函数,
0
≤
t
≤
1
0\leq t \leq1
0≤t≤1.后缀
i
j
k
l
ijkl
ijkl,k表示马蹄铁的状态,i表示第i匹马,j表示马的第j个边,l代表第l个观测曲线。





















 932
932

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








