目的:掌握二叉树遍历算法的应用,熟练使用先序、中序、后序3种递归遍历算法和层次遍历算法进行二叉树的问题求解。
内容:编写一个程序exp7-6.cpp实现以下功能,并对图7.33所示的二叉树进行验证。
(1)输出二叉树b的结点个数。
(2)输出二叉树b的叶子结点个数。
(3)求二叉树b中指定结点值(假设所有节点值不同)的结点层次。
(4)利用层次遍历求二叉树b的宽度。
代码如下:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <algorithm>
using namespace std;
const int MaxSize=10000;
typedef int ElemType;
typedef struct node
{
ElemType data;
struct node * lchild;
struct node * rchild;
}BTNode;
void CreateBTree(BTNode * &b,string str)//创建二叉树
{
BTNode *St[MaxSize],*p;
int top=-1,k,j=0;
char ch;
p=NULL;
b=NULL;
ch=str[j];
while(ch!='\0')
{
switch(ch)
{
case '(':top++;St[top]=p;k=1;break;
case ')':top--;break;
case ',':k=2;break;
default:p=(BTNode *)malloc(sizeof(BTNode));
p->data=ch;
p->lchild=p->rchild=NULL;
if(b==NULL)
b=p;
else
{
switch(k)
{
case 1:St[top]->lchild=p;break;
case 2:St[top]->rchild=p;break;
}
}
}
j++;
ch=str[j];
}
}
void PreOrder(BTNode *b)//先序遍历递归算法
{
if(b!=NULL)
{
printf("%c",b->data);//访问根节点
PreOrder(b->lchild);//先序遍历左子树
PreOrder(b->rchild);//先序遍历右子树
}
}
void InOrder(BTNode *b)//中序遍历递归算法
{
if(b!=NULL)
{
InOrder(b->lchild);//中序遍历左子树
printf("%c",b->data);//访问根节点
InOrder(b->rchild);//中序遍历右子树
}
}
void PostOrder(BTNode *b)//后序遍历递归算法
{
if(b!=NULL)
{
PostOrder(b->lchild);//后序遍历左子树
PostOrder(b->rchild);//后序遍历右子树
printf("%c",b->data);//访问根节点
}
}
int Nodes(BTNode *b)//结点个数
{
if(b==NULL) return 0;
else return Nodes(b->lchild)+Nodes(b->rchild)+1;
}
int Leaves(BTNode *b)//叶子结点个数
{
static int cont=0;
if(b!=NULL)
{
if(b->lchild==NULL&&b->rchild==NULL)
cont++;
Leaves(b->lchild);
Leaves(b->rchild);
}
return cont;
}
int Level(BTNode *b,ElemType x,int h)//结点所在层次
{
int ans;
if(b==NULL) return 0;
else if(b->data==x) return h;
else{
ans=Level(b->lchild,x,h+1);
if(ans!=0) return ans;
else return Level(b->rchild,x,h+1);
}
}
int getWidth(BTNode *b)//最大宽度
{
if(b==NULL) return 0;
int width=0;
queue <BTNode *> q;
q.push(b);
{
while(true)
{
int len=q.size();
if(len==0) break;
width=max(width,len);
while(len)
{
BTNode* t=q.front();
q.pop();
len--;
if(t->lchild!=NULL) q.push(t->lchild);
if(t->rchild!=NULL) q.push(t->rchild);
}
}
}
return width;
}
int main()
{
string str ="A(B(D,E(H(J,K(L,M(,N))),)),C(F,G(,I)))";
BTNode *b;
CreateBTree(b,str);
cout<<"该二叉树的括号表示法为:"<<str<<endl;
int nodes=Nodes(b);
printf("结点个数:%d\n",nodes);
int leaves=Leaves(b);
printf("叶子结点个数:%d\n",leaves);
for(int i=0;i<str.size();i++)
{
if(str[i]>='A'&&str[i]<='Z')
{
int level=Level(b,str[i],1);
printf("结点值为%c的结点在层次%d\n",str[i],level);
}
}
int width=getWidth(b);
printf("最大宽度:%d\n",width);
return 0;
}
运行结果如下:
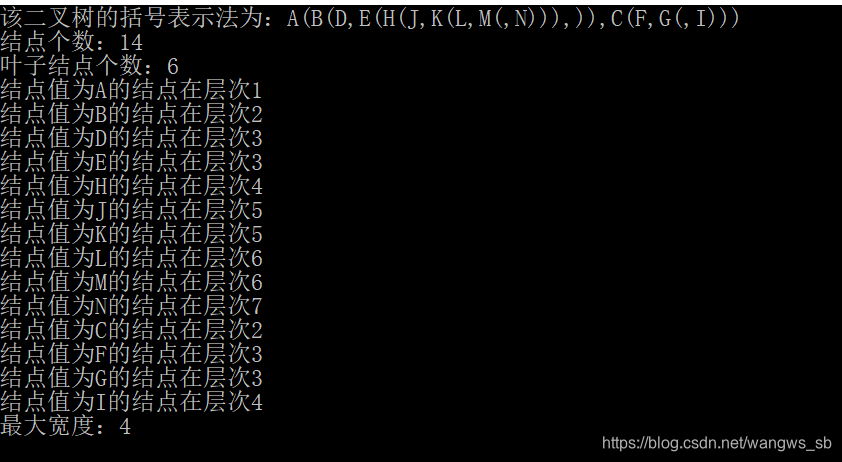





 本文介绍了一个程序,用于实现二叉树的多种遍历算法,包括先序、中序、后序和层次遍历。通过递归算法,程序能够计算二叉树的结点个数、叶子结点个数,查找指定结点的层次,并求得树的最大宽度。
本文介绍了一个程序,用于实现二叉树的多种遍历算法,包括先序、中序、后序和层次遍历。通过递归算法,程序能够计算二叉树的结点个数、叶子结点个数,查找指定结点的层次,并求得树的最大宽度。
















 1031
1031

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








