目的:领会普里姆算法求带权连通图中最小生成树的过程和相关算法设计。
内容:编写一个程序exp8-5.cpp,实现求带权连通图最小生成树的普里姆算法。对于如图8.55所示的带权连通图G,输出从顶点0出发的一颗最小生成树。
[ 数据结构教程(第5版)李春葆 主编 ] 第8章上机练习实验题5
代码如下:
#include <iostream>
#include <cstdio>
using namespace std;
#define INF 0x3f3f3f3f
const int MAXV=1000;
struct MatGraph
{
int edges[100][100];
int n;
};
void prim(MatGraph g,int v)
{
int lowcost[MAXV];
int MIN;
int closest[MAXV],i,j,k;
for(i=0;i<g.n;i++)//给lowcost[]和closest[]置初值
{
lowcost[i]=g.edges[v][i];
closest[i]=v;
}
for(i=1;i<g.n;i++)//找出(n-1)个顶点
{
MIN=INF;
for(j=0;j<g.n;j++)//在(V-U)中找出离U最近的顶点k
if(lowcost[j]!=0&&lowcost[j]<MIN)
{
MIN=lowcost[j];
k=j;//k记录最近顶点的编号
}
printf("边(%d,%d)权为:%d\n",closest[k],k,MIN);//输出最小生成树的一条边
lowcost[k]=0;//标记k已经加入U
for(j=0;j<g.n;j++)//对(V-U)中的顶点j进行调整
if(lowcost[j]!=0&&g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k;//修改数组lowcost和closest
}
}
}
int main()
{
int i,j;
MatGraph g;
g.n=6;
for(i=0;i<=5;i++)
for(j=0;j<=5;j++){
if(i==j) g.edges[i][j]=0;
else g.edges[i][j]=INF;
}
g.edges[0][1]=g.edges[1][0]=5;
g.edges[0][2]=g.edges[2][0]=8;
g.edges[0][3]=g.edges[3][0]=7;
g.edges[0][5]=g.edges[5][0]=3;
g.edges[1][2]=g.edges[2][1]=4;
g.edges[2][3]=g.edges[3][2]=5;
g.edges[2][5]=g.edges[5][2]=9;
g.edges[3][4]=g.edges[4][3]=5;
g.edges[3][5]=g.edges[5][3]=6;
g.edges[4][5]=g.edges[5][4]=1;
printf("普里姆算法所求的最小生成树为:\n");
prim(g,0);
return 0;
}
运行结果如下:
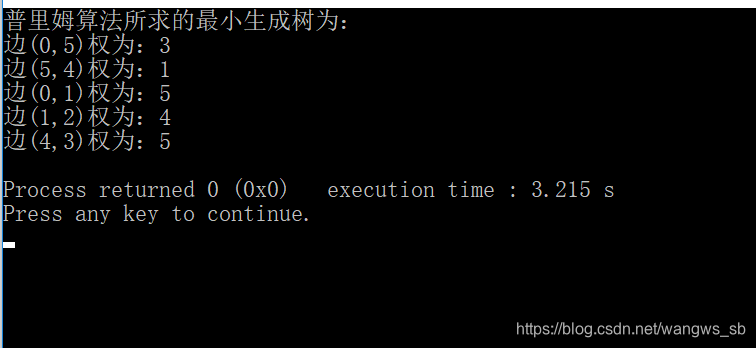





 本文介绍了一个使用普里姆算法求解带权连通图最小生成树的C++程序实例。通过构建一个具体带权连通图并从顶点0开始,程序逐步寻找并输出构成最小生成树的边及其权重。
本文介绍了一个使用普里姆算法求解带权连通图最小生成树的C++程序实例。通过构建一个具体带权连通图并从顶点0开始,程序逐步寻找并输出构成最小生成树的边及其权重。
















 2534
2534










