SVD介绍和代码示例

奇异值分解（SVD）介绍

奇异值分解（Singular Value Decomposition，SVD）是一种矩阵分解技术，广泛应用于推荐系统、图像处理和数据压缩等领域。SVD可以将一个矩阵分解为三个矩阵的乘积，从而提取出数据的潜在结构。

基本原理

给定一个矩阵 AA（通常是一个用户-物品评分矩阵），SVD可以将其分解为三个矩阵的乘积：

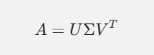
• U：一个正交矩阵，包含了矩阵 AA 的左奇异向量，表示用户特征。
• Σ：一个对角矩阵，包含了奇异值，表示特征的重要性。
• VT：一个正交矩阵的转置，包含了矩阵 AA 的右奇异向量，表示物品特征。

通过保留前 kk 个最大的奇异值（和对应的奇异向量），可以得到一个低秩近似矩阵，从而减少数据的维度，保留主要特征。

Python 代码示例

以下是一个使用 numpy 实现奇异值分解的简单示例。

安装依赖

确保安装了 numpy：

pip install numpy

示例代码

import numpy as np

# 示例评分矩阵（用户 x 物品）
R = np.array([[5, 3, 0, 1],
              [4, 0, 0, 1],
              [1, 1, 0, 5],
              [1, 0, 0, 4],
              [0, 1, 5, 4]])

# 进行奇异值分解
U, sigma, Vt = np.linalg.svd(R, full_matrices=False)

# 将奇异值转换为对角矩阵
Sigma = np.diag(sigma)

# 打印结果
print("U矩阵:\n", U)
print("\nSigma矩阵:\n", Sigma)
print("\nVt矩阵:\n", Vt)

# 选择前k个奇异值进行低秩近似
k = 2  # 选择前2个奇异值
U_k = U[:, :k]
Sigma_k = Sigma[:k, :k]
Vt_k = Vt[:k, :]

# 计算低秩近似
R_approx = np.dot(U_k, np.dot(Sigma_k, Vt_k))

print("\n低秩近似的评分矩阵:\n", R_approx)

# 为用户 0 推荐物品
user_id = 0
recommended_items = np.argsort(R_approx[user_id])[::-1]  # 按照预测评分降序排列
print("\n为用户 0 推荐的物品:\n", recommended_items)

Find More

代码解释

1. 数据准备：创建一个用户-物品评分矩阵 RR。

2. 奇异值分解：使用 numpy.linalg.svd 函数对评分矩阵进行奇异值分解，得到 UU、ΣΣ 和 VTVT。

3. 奇异值矩阵：将奇异值转换为对角矩阵 ΣΣ。

4. 低秩近似：

   • 选择前 kk 个奇异值和相应的奇异向量。
   • 计算低秩近似的评分矩阵 RapproxRapprox​。

5. 推荐物品：为指定用户（例如用户 0）推荐物品，根据低秩近似的评分矩阵排序，输出推荐物品的索引。

总结

奇异值分解是一种强大的降维技术，能够有效提取数据中的潜在特征。在推荐系统中，SVD可以通过低秩近似来生成个性化推荐。以上示例展示了如何使用 SVD 实现推荐功能，实际应用中可以根据需求进行扩展和优化。