博客主要探讨L1正则化产生稀疏矩阵的原因。从图像角度，L1等值线是方形，相交大概率在顶点，顶点在坐标轴上使其他参数为0；从数学角度，对损失函数求梯度，L1正则使损失函数在0附近反复，极小值处梯度为0，导致许多参数解为0，使模型稀疏。
L1正则化：
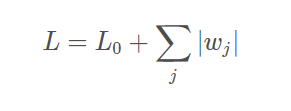
为啥会产生稀疏矩阵：（看图）
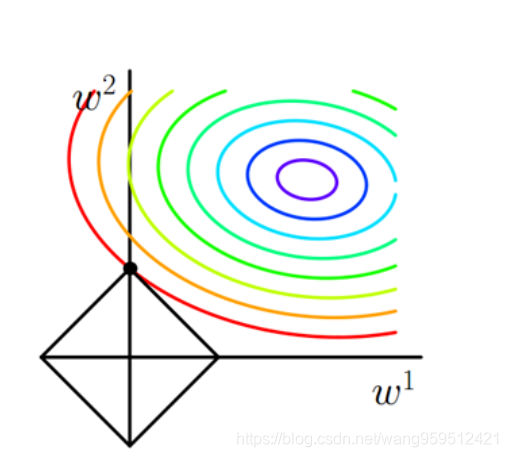
L1的等值线是方形,等值线相交时很大概率上出现在顶点处，而顶点都在坐标轴上，因此必有其他参数为0，所以用L1正则的解具有稀疏性.
数学解释：
对损失函数求梯度：
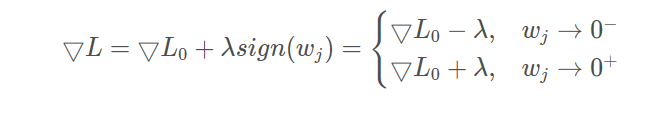
通俗一点的理解就是，L1正则会使损失函数在0附近反复经过，当其大于0时，loss值会减小；当其小于0时，loss值又会增大。
我觉得还是图像生动一点，极小值产生时，也就是说损失函数时是一个凹图（没找到图。。）
，即此处的损失函数的导数是为0的，不就是梯度为0吗？梯度不就是w嘛。。。所以会产生稀疏解（就是导致许多参数的解变为0，这样模型就变得稀疏了）
扫一扫
2208
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
