基于并行前缀加法器的低功耗改进型移位相乘器设计
1. 引言
乘法是算术运算中的基本数学运算之一。它是数字信号处理器和微处理器1中的主要功能之一。乘法器对整个数字系统的性能有显著影响。乘法时间以及乘法器所需的硬件资源相比其他算术运算要更多2。由于近年来技术的进步,许多研究人员一直在致力于设计一种快速且面积和功耗高效的乘法器。在设计乘法器时,总是在高速与低功耗之间进行权衡。在数字电路中,降低功耗和提高处理速度是信号处理应用中的两个主要考虑因素。在超大规模集成电路设计中,通过降低占总功耗主要部分的动态功耗,可以节省功耗。
在本研究中,通过修改旁路零,直接馈送A(BZ‐FAD)乘法器提出了一种低功耗乘法器设计。该结构由于设计中切换活动减少,因此功耗更低。为了加快乘法器中的部分积相加过程,还提出了一种并行前缀加法器。本文其余部分安排如下:第2节简要回顾了不同的乘法器和前缀加法器。第3节介绍了传统和所提出的移位相乘器的详细信息。第4节介绍了一种用于移位相乘器的新型并行前缀加法器。第5节讨论了仿真和综合结果。最后,第6节对全文进行了总结。
2. 以往工作
过去已经开发出许多高效的乘法器。沈和陈3通过使用布斯算法减少部分积的切换活动,开发出一种低功耗乘法器。陈等4提出了一种低功耗二进制补码乘法器。采用基数‐4布斯算法来降低部分积的切换活动。王等5利用左右算法开发了一种固定宽度乘法器。它减少了部分积以提高乘法速度,但代价是功耗较高。志俊和 Ercegovac6提出了一种基于多种技术组合的线性阵列乘法器设计。该结构功耗较低,但面积和延迟增加。陈和楚7通过在乘法器的布斯解码器和压缩树上应用虚假功耗抑制技术(SPST),提出了一种低功耗高速乘法器,但这些结构需要较大的面积。克拉德和塔伊8对两种使用超前进位加法器和波纹进位加法器进行部分积相加的32位乘法器进行了性能分析。Dastjerdi等9为移位相乘器开发了BZ‐FAD。该结构减少了乘法器中的切换活动,从而节省了功耗。Saha等10提出了一种基于成对算法的低功耗高速8位乘法器。由于采用了波动流水线,该设计的吞吐量较高。Liu等11为容错应用提出了一种近似乘法器。该结构功耗较低且关键路径较短。莫汉蒂和提瓦里12为数字信号处理应用提出了一种改进的概率估计偏差(PEB)基数‐4布斯乘法器。同时还提出了一种适用于PEB乘法器的高效加法器。该加法器使用较少的逻辑资源,并提供了最优关键路径延迟。邵和李13开发了一种能效和面积效率高的16位固定宽度布斯乘法器和平行器。还引入了一种基于阵列的近似算术计算(AAAC)的通用模型,以指导乘法器和平行器的设计。He等14基于输入序列的条件概率(CPIS)开发了一种高速固定宽度布斯乘法器。该方法提高了操作速度并降低了电路开销。Shabbir等15使用达达算法开发了一种低功耗高速乘法器。全加器被设计用于该乘法器中。通过为乘法器设计触发器,减少了输出中的毛刺。
文献中已提出了多种用于并行前缀计算的设计。Efstathiou等16基于林17提出的方程开发了一种用于加法的混合前缀结构。迪米特拉科普oulos 和尼科洛斯 18提出了一种基于改进的Ling方程的并行前缀加法器结构。该结构速度快,并减少了扇出需求。普尔尼玛和帕斯卡兰19通过将拉德纳和费希尔20提出的偶数位前缀结构与科格和斯通21提出的奇数位结构相结合,开发了一种加法器结构。所有这些关于前缀加法器的前期工作都集中在结构速度上,而对面积和功耗的关注较少。因此,本文提出了一种基于并行前缀技术的高效加法器设计。
3. 移位相乘器
移位相乘法包括两个过程:部分积生成和求和。在此过程中,最多涉及四种主要的切换活动9。假设一个寄存器保存被乘数,另一个寄存器保存乘数,则在传统移位相乘法过程中发生的切换活动包括:(a) 乘数位的移位 (b) 加法器中的操作 (c) 部分积位的移位 (d) 多路复用器中零与被乘数位之间的切换以进行加法运算。
乘法器中的开关活动占功耗的较大部分。乘法器的功耗可以表示为4
$$P_{switching} = \alpha \cdot C \cdot V^2_{dd} \cdot f_{clk}$$
其中 $f_{clk}$为工作频率, $V_{dd}$为电源电压, $C$为负载电容, $\alpha$为切换活动参数。
通过最小化乘法器中的任何切换活动,可以降低功耗。
3.1. 旁路零值直接输入A(BZ-FAD)乘法器
Dastjerdi et al.9 对传统的移位相加乘法器进行了改进,并提出了BZ‐FAD,以降低乘法器中的切换活动。如图1所示,在BZ‐FAD结构中,寄存器A存储 k‐位的被乘数,寄存器B存储 n‐位的乘法器。在BZ‐FAD中发生的切换活动包括:
3.1.1. 寄存器B内容的移位
在传统的移位相加乘法器22 ,中,寄存器B的内容在每个周期向右移动一位位置,并且每次检查B的 0 th位。如果该 0 th位为‘1’,则将寄存器A的内容与前一个部分积相加,否则加上零。寄存器内容的移位导致了开关活动。为了避免这一点,在BZ‐FAD中,一个多路复用器M3在每个周期使用独热编码总线选择器选择热位,即B的 0 th位。

从而消除了寄存器内容的移位。结构中的环形计数器用于在 nth周期中选择 Bn。在考虑高位乘法器(如16位或更高)时,计数器的平均切换因子低于乘法器位的移位。
3.1.2. 加法器中的切换活动
在传统乘法器中,部分积根据B的 0th位是加到寄存器A的内容上还是加到零上。而在BZ‐FAD中,该操作使用两个寄存器,即Feeder和Bypass。如果B的 0th位为‘0’,则将Bypass寄存器的内容直接送至多路复用器M1,跳过加法操作;如果该位为‘1’,则将来自Feeder寄存器的前一个部分积与寄存器A的内容相加,并将结果送至多路复用器M1。随后,来自M1的部分积被存储到Feeder和 Bypass寄存器中。在此过程中,避免了与零的加法操作。
3.1.3. 部分积的移位
在传统的移位‐相加乘法器中,部分积的内容在每个时钟周期向右移位。部分积位的移位导致了较大的功耗。在BZ‐FAD乘法器中,通过仅处理最重要的部分积位来减少切换活动。乘积位的下半部分在最初几个周期内即已确定。在每个周期中,部分积的 0 th位(P P)被存储在一个 P latch 中,剩余位则存储在Feeder和 Bypass中以供进一步处理。剩余位在后续周期中被确定,并存储在锁存器中。使用环形计数器来打开正确的锁存器。
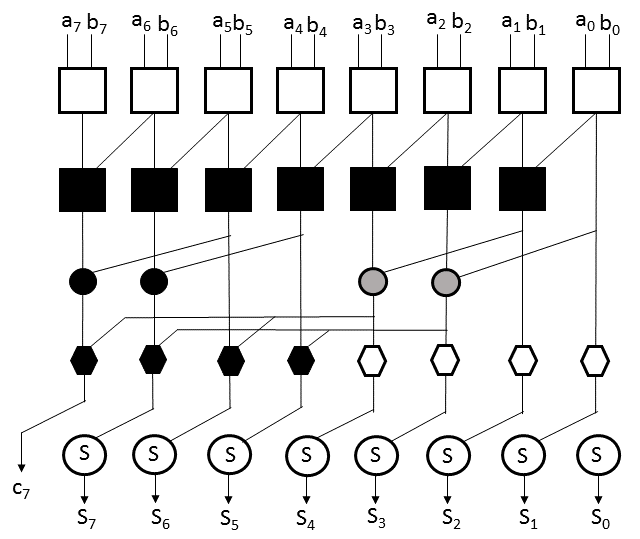
3.2. 提出的乘法器
为了获得面积功耗高效结构,对BZ‐FAD乘法器进行了改进。提出的乘法器旁路零输入被乘数直接相乘如图2所示。与图1中的结构相比,移除了若干组件以减少延迟。BZ‐FAD中的由多路复用器M2选择的乘法器位、D触发器以及多路复用器 M3被移除,以减小面积和延迟。图1中用于选择寄存器B的位并打开相应锁存器的环形计数器及多路复用器M3被取消,取而代之的是采用二进制计数器,以减小面积并简化控制复杂度。旁路寄存器在提出的结构中被乘积寄存器所替代。控制器模块在接收到启动信号时控制乘法操作,并在复位引脚有效时进行复位。
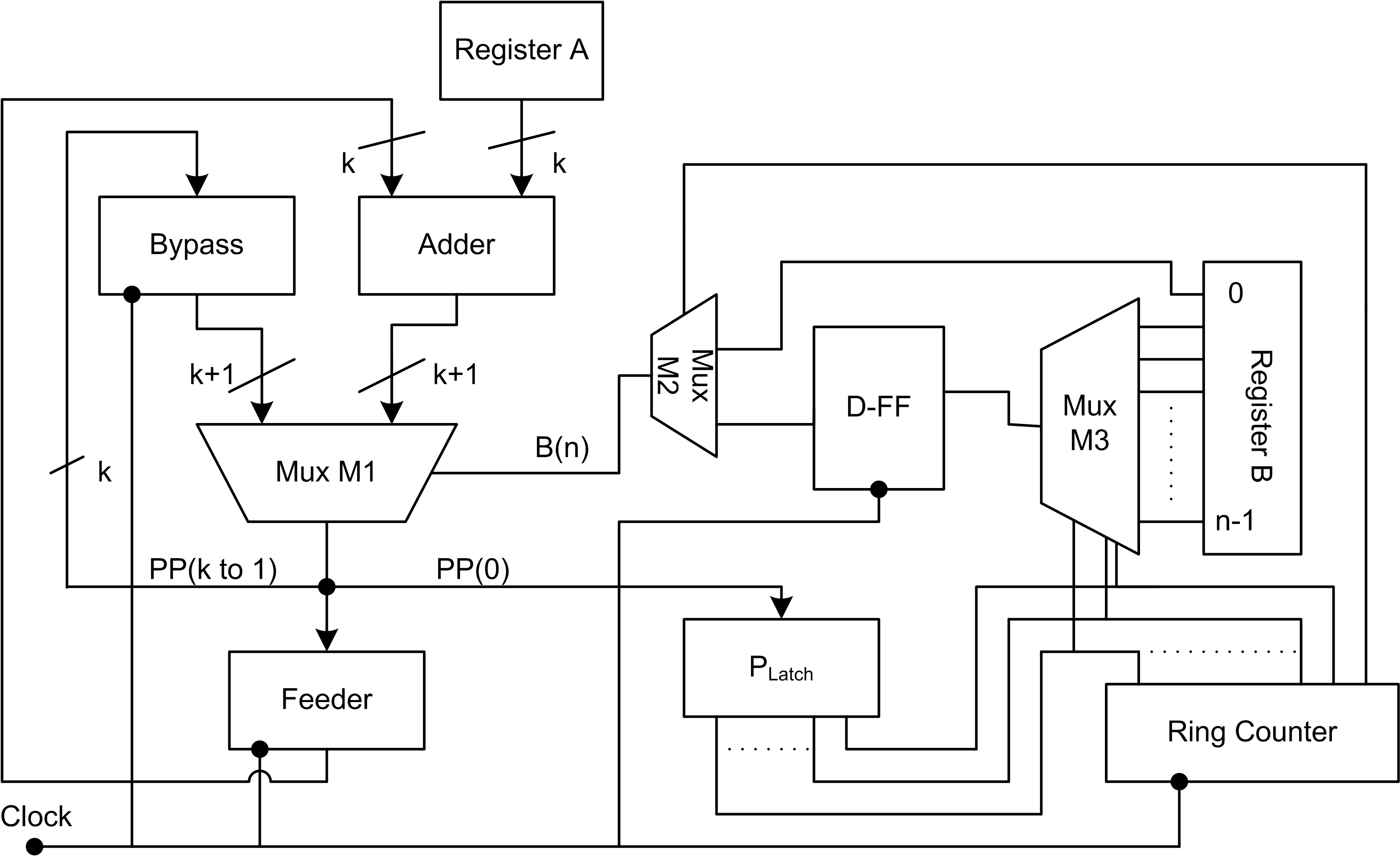
3.2.1. 乘数位的移位
将乘法器位移位以检查 0 th位会导致开关活动。因此,为了降低这种开关活动,如图2所示采用了控制器,该控制器用于检查乘法器位是零还是一。该控制器包含一个与时钟同步的二进制计数器。在每个时钟的上升沿,计数器递增,并选择乘法器模块中的特定位位置。通过将该位置的位与一进行与操作来检查其为零或一。控制器控制数据从馈送寄存器流向多路复用器或加法器。多路复用器根据乘法器位选择加法器输出或存储在Feeder寄存器中的前一个部分积。如果乘法器位为 ‘0’,则加法执行被跳过,且存储在Feeder寄存器中的前一个部分积直接馈送到多路复用器;否则,前一个部分积与被乘数的和被馈送到多路复用器。此处,传统移位‐加法乘法器中对零的加法操作被消除,而是直接馈入被乘数。此过程最小化了加法器中的开关活动。
3.2.2. 部分积的移位
在每个时钟周期中,乘积的一位被最终确定。来自多路复用器的部分积的 0th位直接存储到Product寄存器中,其余位则向右移动一位位置,并重新存储回Feeder寄存器以进行后续处理。在后续周期中,乘积的剩余最低有效位被逐次确定并存储到 Product寄存器中。该方法无需对乘积的低半部分位进行移位,因此这些位可直接存储到Product寄存器中。乘积的高半部分位在处理完成后被转移到Product寄存器。与传统乘法器中整个部分积值都需要向右移位的方法相比,此过程降低了开关活动。控制器模块中的计数器选择Product寄存器中的位位置,以便在每个时钟周期存储一位乘积。然而,在BZ‐FAD中,打开各个锁存器并存储乘积位的过程较为复杂,从而增加了设计复杂度。
4. 并行前缀加法器
乘法器的性能取决于部分积求和的速度。提高性能的方法之一是使用并行前缀加法器来加快求和速度。这些并行前缀加法器提高了进位传播的速度,从而加快了求和过程。
林17提出了一种并行加法器,其在前缀加法中比传统加法器更快。通过修改先行进位方程,实现了显著的硬件节省。该技术的关键在于计算伪进位Hi而非传统进位 ci,从而节省了一个逻辑单元。伪进位的表达式如下
$$H_i = g_i + g_{i-1} + p_{i-1} \cdot g_{i-2} + p_{i-1} \cdot p_{i-2} \cdot g_{i-3} + \cdots + p_{i-1} \cdot p_{i-2} \cdots p_1 \cdot g_0$$
其中 $g_i$是每一位位置 i的进位产生位, $p_i$是每一位位置 i的进位传播位,对于 $0 \leq i \leq n - 1$。尽管伪进位的计算相比传统进位更简单,但和计算较为复杂。这表示为
$$Sum_i = d_i \oplus (p_{i-1} \cdot H_{i-1})$$
林 et al. 23 修改了林方程,以利用伪进位 $H_i$ 生成真实进位 $c_i$,从而使最终的和计算变为简单的异或运算
$$Sum_i = d_i \oplus c_{i-1}$$
考虑基于林方程的加法器中第三位位置的伪进位方程
$$H_3 = g_3 + g_2 + p_2 \cdot g_1 + p_2 \cdot p_1 \cdot g_0$$
由于 $g_i \cdot p_i = g_i$,公式(5)可以写成
$$H_3 = g_3 + g_2 + p_2 \cdot p_1 \cdot g_1 + p_2 \cdot p_1 \cdot g_0$$
$$= (g_3 + g_2) + p_2 \cdot p_1 \cdot (g_1 + g_0)$$
令
$$G^
i = g_i + g
{i+1} \quad \text{和} \quad P^
i = p_i \cdot p
{i-1}$$
其中 $G^
_i$和 $P^
i$分别是中间生成位和中间传播位 18。
考虑 $g
{-1} = p_{-1} = 0$和 $G^
_s = P^
s = 0$, for $s < 0$;公式(7)可以用结合算子表示为
$$H_3 = G
{3:2} + P_{2:1} \cdot G_{1:0}$$
$$= (G_{3:2}, P_{2:1})(G_{1:0}, P_{0:-1})$$
$$= (G^
_2)(G^
0)$$
真实进位可以表示为
$$c_3 = H_3 \cdot p_3$$
偶数索引位位置(Hi)和奇数索引位位置(Hi+1)的伪进位如下所示
$$H_i = (G^
_i, P^
{i-1}) (G^
_{i-2}, P^
{i-3}) \cdots (G^
_0, P^
{-1})$$
$$H_{i+1} = (G^
_{i+1}, P^
i) (G^
_{i-1}, P^
{i-2}) \cdots (G^
_1, P^
_0)$$
所有位的真实进位通过将伪进位与传递位19,23进行与操作来计算。然而,这种计算进位的方法增加了加法器结构的面积和功耗。
4.1. 提出的方法
一种基于改进的林方程概念的高效快速并行前缀加法器设计已提出,适用于8位、 16位和32位乘法器。该提出的方法通过将低半部分位的伪进位与相应的低半部分 传递位进行与操作来计算真实进位,其方程如下所示
$$c_i = H_i \cdot p_i$$
对于高半部分位,通过将伪进位用中间生成位和中间传播位表示,并结合 $i > k > j$ 来计算进位。
$$c_i = (G_{i:k} + P_{i-1:k-1} \cdot G_{k-1:j+1}) \cdot p_i$$
例如,16位加法器中第八位的进位获取如下:
$$H_8 = (G_{8:7}, P_{7:6})(G_{6:3}, P_{5:2})(G_{2:-1}, P_{1:-2})$$
$$= (G_{8:7} + P_{7:6} \cdot G_{6:-1}, P_{7:6} \cdot P_{5:-2})$$
$c_8$现在可以写成
$$c_8 = (G_{8:7} + P_{7:6} \cdot G_{6:-1}) \cdot p_8$$
类似地, $c_9$到 $c_{15}$可以表示为
$$c_9 = (G_{9:8} + P_{8:7} \cdot G_{7:0}) \cdot p_9$$
$$c_{10} = (G_{10:7} + P_{9:6} \cdot G_{6:-1}) \cdot p_{10}$$
$$c_{11} = (G_{11:8} + P_{10:7} \cdot G_{7:0}) \cdot p_{11}$$
$$c_{12} = (G_{12:7} + P_{11:6} \cdot G_{6:-1}) \cdot p_{12}$$
$$c_{13} = (G_{13:8} + P_{12:7} \cdot G_{7:0}) \cdot p_{13}$$
$$c_{14} = (G_{14:7} + P_{13:6} \cdot G_{6:-1}) \cdot p_{14}$$
$$c_{15} = (G_{15:8} + P_{14:7} \cdot G_{7:0}) \cdot p_{15}$$

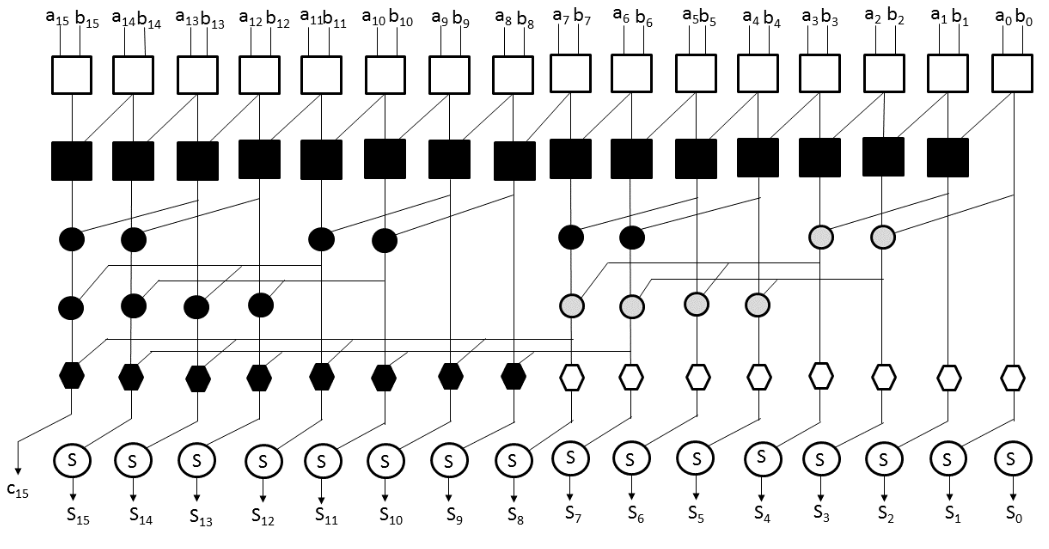
基于改进的Ling方程的所提出的并行前缀16位加法器如图3所示。与基于Ling方程 计算伪进位(hi)的其他并行前缀加法器不同,该加法器计算真实进位(ci),从而简化了最终和的计算级。它在每个和位计算中节省了一个逻辑门,从而减少了 加法器单元的面积。
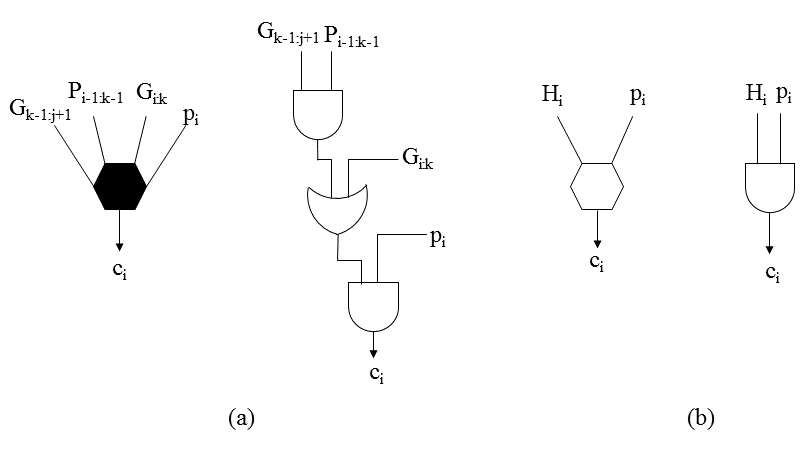
图4(a)中的白色方块计算generate $(g_i)$、propagate $(p_i)$和half-sum $(d_i)$位,由以下给出
$$g_i = x_i \,\text{AND}\, y_i$$
$$p_i = x_i \,\text{OR}\, y_i$$
$$d_i = x_i \,\text{XOR}\, y_i$$
 生成、传播和半和计算节点。(b) 中间生成和传播计算节点18)
生成、传播和半和计算节点。(b) 中间生成和传播计算节点18)
图4(b)中的黑色方块计算公式(8)中表达的中间生成位和中间传递位。
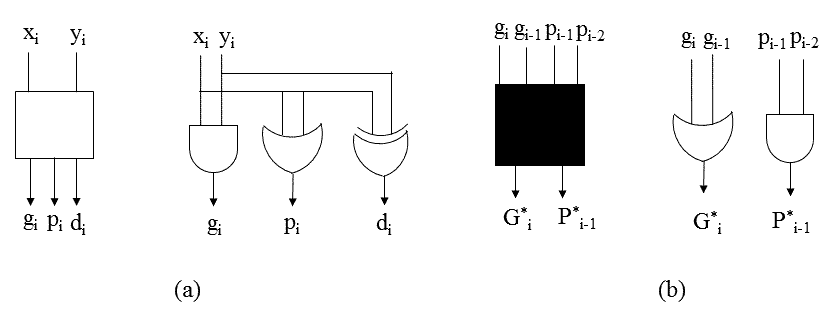
图5(a) 中显示了一个灰色圆圈,用于计算组进位生成位,而图5(b) 中的黑色圆圈 则用于计算组进位生成位和组进位传播位。
$$G_{i:j} = G_{i:k} + G_{m:j} \cdot P_{i:k}$$
$$P_{i:j} = P_{i:k} \cdot P_{m:j}$$
这里, $i > k > m > j$
 组生成计算节点。 (b) 组生成和传播计算节点24)
组生成计算节点。 (b) 组生成和传播计算节点24)
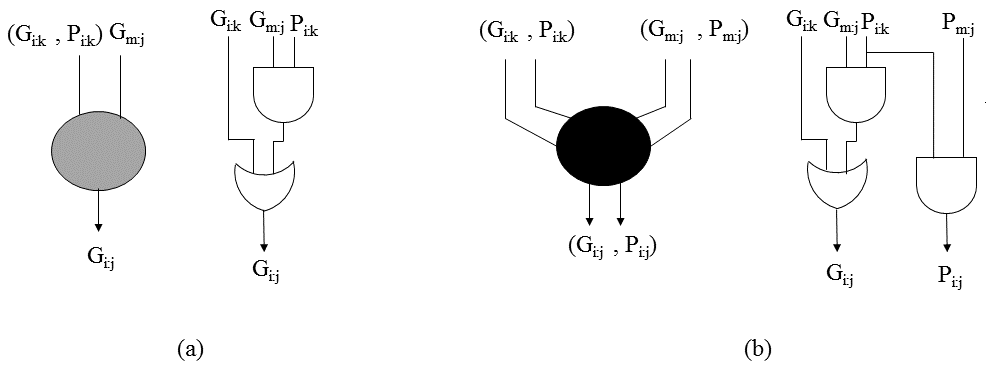
计算真实进位的单元如图6所示。图6(a)中的黑色六边形是提出的进位单元,用于 计算由公式16表示的上半部分实际进位。由于只有中间进位生成项形成伪进位, 因此可以从中消除中间进位传播项的计算,从而节省两个门电路。低半部分位的 真实进位通过将伪进位与相应的传递位进行与操作直接获得,如公式15所示,见 图6(b)。
 用于计算上半部分真实进位的提出的进位单元。 (b) 用于计算下半部分真实进位的提出的进位单元)
用于计算上半部分真实进位的提出的进位单元。 (b) 用于计算下半部分真实进位的提出的进位单元)
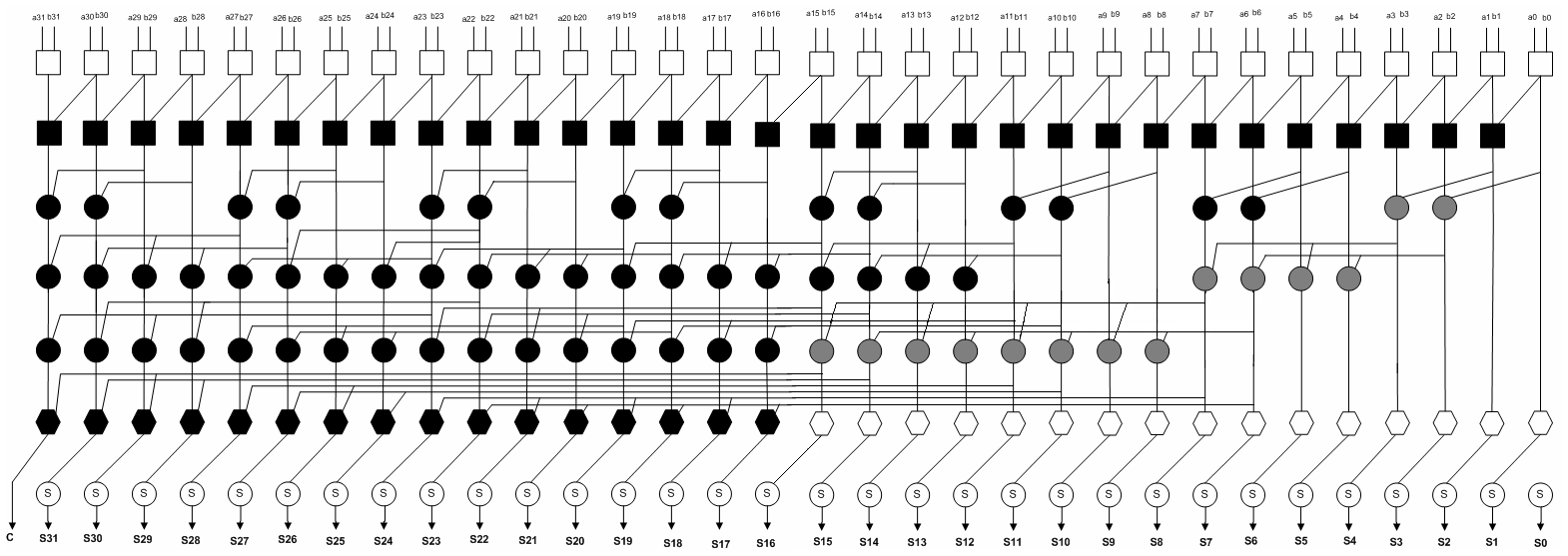
基于改进的Ling方程的8位和32位提出的并行前缀加法器分别如图7和图8所示。
这些并行前缀加法器具有规则结构和较少的门数。它们的最小逻辑深度为 $\log_2 n$。 所有结构的扇出均为四,这减少了传播延迟和门的负载。
5. 结果与讨论
提出的乘法器采用VHDL建模,并使用台积电90纳米和180纳米CMOS技术进行综 合。形式验证通过Cadence NC-Simulator完成,结果在MATLAB中进行了验证。 对于8位和16位乘法器及加法器,进行了穷尽验证;对于32位乘法器及加法器,提 供了50,000个随机测试向量,确认了其正确性。进行了静态时序分析,并记录了 延迟。使用Cadence RTL编译器进行综合,以观察功耗和面积。功耗估计基于正常 情况下的开关活动在 100MHz处生成分布式随机数集合。衍生出的网表和设计约束被输入到Cadence Encounter工具中以获得布局,最后在优化后从布局中提取RC寄生参数信息。
| 结构 | 功耗(µW/MHz) | 延迟(ns) |
|---|---|---|
| BZ-FAD 9 (130纳米) | 7.576 | 9.76 |
| 提出的结构(90纳米) | 1.45 | 2.51 |
| 提出的结构(180纳米) | 10.1 | 5.15 |
表1. 功耗和延迟比较。
提出的结构速度快且高效,在功耗和延迟之间实现了良好的平衡。
| 结构 | 技术 | 功耗 (mW) | 延迟 (ns) | Area |
|---|---|---|---|---|
| 提出的结构 | 90nm | 0.08 | 2.32 | 1,095 (µm²) |
| 使用提出并行加法器的BZ-FAD | 90nm | 0.07 | 2.76 | 1,121 (µm²) |
| 使用RCA的提出乘法器 | 90nm | 0.06 | 4.33 | 1,147 (µm²) |
| Mohanty12 | 90nm | 0.01 | 11.6 | 2,295 (µm²) |
| Shabbir15(4位乘法器) | 90nm | 1.09 | 0.22 | 7,752 (µm²) |
| 提出的结构 | 180纳米 | 0.5 | 4.24 | 4,531 (µm²) |
| 使用提出并行加法器的BZ-FAD | 180纳米 | 0.4 | 4.86 | 4,565 (µm²) |
| 使用RCA的提出乘法器 | 180纳米 | 0.4 | 5.86 | 4,925 (µm²) |
| He 14 | 180纳米 | 1.87 | 6.47 | 3,350 (µm²) |
| Saha10 | 180纳米 | 18.54 | 3.24 | 9,40,800 (µm²) |
| Chen25 | 180纳米 | 0.92 | 3.09 | 6,552 (µm²) |
| Chen26 | 180纳米 | 0.88 | 9.79 | 3,927 (µm²) |
| Li27 | 180纳米 | 0.88 | - | 3,927 (µm²) |
| Kuo28 | 180纳米 | 2.14 | 2.24 | 92,449 (µm²) |
| Wang29 | 130纳米 | 0.3 | 3.56 | 2,005 (µm²) |
| Kang30 | 130纳米 | 6.38 | 3.03 | 4,030 (µm²) |
| Lee31 | 130纳米 | 0.53 | 50.0 | 7,850 (gates) |
表2. 8位乘法器的面积和功耗比较。
| 结构 | 技术 | 功耗 (mW) | 延迟 (ns) | Area |
|---|---|---|---|---|
| 提出的结构 | 90nm | 0.1 | 2.51 | 2,107 (µm²) |
| 使用提出并行加法器的BZ-FAD | 90nm | 0.1 | 4.09 | 2,231 (µm²) |
| 使用RCA的提出乘法器 | 90nm | 0.1 | 5.08 | 2,487 (µm²) |
| Shao13 | 90nm | 1.2 | 2.99 | 3,755 (µm²) |
| Mohanty12 | 90nm | 0.06 | 20.0 | 7,763 (µm²) |
| Paul32 | 90nm | 5.5 | 1.15 | - |
| Hsu33 | 90nm | 9.0 | - | 27,950 (µm²) |
| Ho34 | 65nm | 71.89 | 0.91 | 1,36,926 (Transistors) |
| 提出的结构 | 180纳米 | 1.1 | 5.15 | 8,669 (µm²) |
| 使用提出并行加法器的BZ-FAD | 180纳米 | 1.0 | 8.08 | 8,932 (µm²) |
| 使用RCA的提出乘法器 | 180纳米 | 0.9 | 9.43 | 8,987 (µm²) |
| He14 | 180纳米 | 9.79 | 11.93 | 13,006 (µm²) |
| Chen35 | 180纳米 | 8.3 | 10.0 | 4,71,270 (µm²) |
| He36 | 180纳米 | 1.6 | 10.0 | 1,09,872 (µm²) |
| Chen25 | 180纳米 | 3.9 | 5.23 | 19,832 (µm²) |
| Chen26 | 180纳米 | 4.08 | 18.28 | 14,175 (µm²) |
| Li27 | 180纳米 | 4.07 | - | 14,175 (µm²) |
| Kuo28 | 180纳米 | 9.11 | 4.71 | 3,67,908 (µm²) |
| Paul32 | 180纳米 | 17.1 | 3.08 | 1,16,800 (µm²) |
| Wang29 | 130纳米 | 1.35 | 5.76 | 6,683 (µm²) |
| Kang30 | 130纳米 | 25.27 | 4.42 | 14,859 (µm²) |
| Lee31 | 130纳米 | 1.04 | 50.0 | 7850 (Gates) |
表3. 16位乘法器的面积和功耗比较
| 结构 | 技术 | 功耗 (mW) | 延迟 (ns) | Area |
|---|---|---|---|---|
| 提出的结构 | 90nm | 0.3 | 2.97 | 4,346 (µm²) |
| 使用提出并行加法器的BZ-FAD | 90nm | 0.4 | 7.11 | 4,455 (µm²) |
| 使用RCA的提出乘法器 | 90nm | 0.2 | 8.13 | 4,265 (µm²) |
| CSA-PPC37 | 90nm | 26.6 | 8.07 | 50,408 (µm²) |
| RCA-PPC37 | 90nm | 27.7 | 6.04 | 50,360 (µm²) |
| Basiri38 | 90nm | 0.58 | 2.5 | 25,000 (µm²) |
| 双精度 BW39 | 65nm | 24.2 | 2.8 | 53,000 (µm²) |
| 双精度 MB39 | 65nm | 38.0 | 2.68 | 53,000 (µm²) |
| 提出的结构 | 180纳米 | 2.36 | 5.67 | 17,816 (µm²) |
| 使用提出并行加法器的BZ-FAD | 180纳米 | 2.3 | 9.24 | 18,145 (µm²) |
| 使用RCA的提出乘法器 | 180纳米 | 2.62 | 10.0 | 17,897 (µm²) |
| He14 | 180纳米 | 7.3 | 20.0 | 5,68,512 (µm²) |
| CSA-PPC37 | 180纳米 | 161.98 | 19.96 | 1,93,489 (µm²) |
| RCA-PPC37 | 180纳米 | 171.8 | 12.55 | 1,97,744 (µm²) |
| Basiri38 | 180纳米 | 0.85 | 4.7 | 34,000 (µm²) |
| Huang6 | 180纳米 | 40.65 | 7.25 | 74,598 (µm²) |
| Wang40 | 130纳米 | 12.1 | 3.0 | 85,983 (µm²) |
| 双精度 BW39 | 130纳米 | 7.3 | 3.99 | 99,000 (µm²) |
| 双精度 MB39 | 130纳米 | 11.1 | 3.75 | 1,20,000 (µm²) |
表4. 32位乘法器的面积和功耗比较
| 技术 | 面积 (µm²) | 延迟 (ns) | 功耗 (mW) |
|---|---|---|---|
| 90nm | 1,095 | 2.32 | 0.08 |
| 180纳米 | 4,531 | 4.24 | 0.5 |
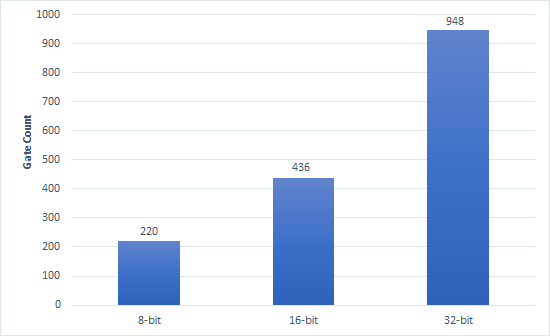
表5。8位乘法器的面积、延迟和功耗估计。
| 技术 | 面积 (µm²) | 延迟 (ns) | 功耗 (mW) |
|---|---|---|---|
| 90nm | 2,107 | 2.51 | 0.1 |
| 180纳米 | 8,669 | 5.15 | 1.1 |
表6. 16位乘法器的面积、延迟和功耗估计。
| 技术 | 面积 (µm²) | 延迟 (ns) | 功耗 (mW) |
|---|---|---|---|
| 90nm | 4,346 | 2.97 | 0.3 |
| 180纳米 | 17,816 | 5.67 | 2.3 |
表7. 32位乘法器的面积、延迟和功耗估计。
| 技术 | 面积 (µm²) | 延迟 (ns) | 功耗 (mW) |
|---|---|---|---|
| 90nm | 279 | 0.87 | 0.006 |
| 180纳米 | 1131 | 1.82 | 0.05 |
表8 . 8位加法器的面积、延迟和功耗估算 dder。
| 技术 | 面积 (µm²) | 延迟 (ns) | 功耗 (mW) |
|---|---|---|---|
| 90nm | 651 | 1.14 | 0.015 |
| 180纳米 | 2621 | 2.29 | 0.12 |
表9. 16位加法器的面积、延迟和功耗估计。
| 技术 | 面积 (µm²) | 延迟 (ns) | 功耗 (mW) |
|---|---|---|---|
| 90nm | 1661 | 1.48 | 0.039 |
| 180纳米 | 6600 | 2.92 | 0.31 |
表10. 32位加法器的面积、延迟和功耗估计。
6. 结论
本文提出了一种针对8位、16位和32位的面积功耗高效的Bypass Zero Feed Multiplicand Directly乘法器。该设计以一定的延迟为代价,实现了功耗和面积节省。比较结果表明,16位乘法器的功耗最多可降低31%,面积节省可达33%。在乘法器中采用并行前缀加法器进行部分积相加,从而实现了高效设计。本文还提出了基于改进的Ling方程的8位、16位和32位加法器设计。这些加法器具有最少门数。从而实现面积节省。它具有规则结构和降低的互连复杂度。所提出的乘法器在面积和功耗方面均高效;可用于数字信号处理器或任何信号处理应用中。




















 40
40

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








