基于四进制超前进位加法器的低功耗高速乘法器的设计与实现
摘要
随着半导体技术速度的提升,嵌入式和便携式数字信号处理(DSP)系统的需求日益增加。乘法器几乎是每个DSP应用中最关键的部分。因此,高速DSP需要低功耗、高速的乘法器。阵列乘法器是其中一种快速乘法器,因为它具有规则结构且易于设计。阵列乘法器通过使用全加器和半加器来实现无符号数的乘法。它依赖于部分和的前级计算以产生最终输出。因此,产生输出的延迟较大。在先前的研究中,采用互补金属氧化物半导体(CMOS)超前进位加法器(CLA)以及基于CMOS电源门控的CLA,以最大化乘法器的速度,并在最小延迟下改善功耗。CMOS逻辑基于基数2(二进制)数系统。在算术运算中,二进制数系统的主要问题与进位相关。可以采用高基数数系统,如四进制有符号数(QSD),以在无进位的情况下执行算术运算。所提出的系统设计了一种采用四进制有符号数系统(QSD)的阵列乘法器,并结合基于QSD的超前进位加法器(CLA),以提高性能。通常,四进制器件相比二进制逻辑器件,处理相同数量数据所需的电路更简单。因此,在CLA中应用四进制逻辑可提高加法器的速度和高吞吐量。在阵列乘法器架构中,使用基于QSD的超前进位加法器替代全加器。这有助于降低功耗并实现快速乘法。使用Tanner EDA工具在180纳米技术下对所提出的乘法器电路进行仿真。从面积、功耗延迟积(PDP)和平均功耗方面,将所提出的QSD CLA乘法器与电源门控CLA和CLA乘法器进行了比较。
关键词 :阵列乘法器,数字信号处理(DSP),吞吐量,超前进位加法器(CLA)与四进制逻辑。
引言
乘法是大多数数字信号处理(DSP)应用中的主要操作。在处理器中,乘法器速度决定了数字信号处理器速度[1‐2]。通过设计高效乘法器,可以提升复杂数字信号处理和微处理器系统性能[3]。
改进型Booth乘法器、阵列乘法器、二进制乘法器是乘法器的类别。每种乘法器包含不同的结构和算法。由于性能要求,乘法器实现是一项具有挑战性的任务。在面积、功耗、延迟和吞吐量方面,乘法器必须对宽位宽范围保持高效。
在集成电路中,实现阵列乘法器仅需较小空间。在数字集成电路中,这是一种有效的乘法方法[4‐5]。
移位部分积累加和部分积评估是乘法中使用的原则。该操作需要连续进行加法运算。
加法器是设计乘法器所需的重要组件。它可以是行波进位加法器(RCA)[6],超前进位(CLA)[7‐8],进位选择[9‐10],跳过进位和进位保存加法器(CSA)[11‐12]。许多研究工作分析了各种高速加法器的性能。超前进位加法器能够更快速地计算进位。
根据输入信号,超前进位算法可计算出下一阶段的进位。因此,加法操作可以非常快速地完成 [13‐15]。
在阵列乘法器架构中,使用基于QSD的超前进位加法器替代全加器。这有助于实现低功耗和快速乘法。
加法算术操作决定了任何处理器的速度。研究人员广泛使用四进制有符号数系统(QSD),以提升加法操作的速度。QSD数制可实现无借位减法和无进位加法 [16‐17]。
当位数增加时,进位传播和生成限制了二进制数系统的计算速度。QSD数制可实现无借位减法和无进位加法。QSD [18] 中每个数字使用‐3到3的数形式表示。在恒定延迟下,可在数字实现中实现128、256及更多数量的大量数字。QSD数制具有以下主要优点:减少互连和晶体管数量。这降低了系统的整体复杂度。该技术可用于实现乘法器和加法器,具有有效面积和速度优势。
2. 提出的方法
2.1 QSD逻辑门
二进制逻辑系统被用来构建一种接近二进制数系统的四进制逻辑系统。这是一种四进制系统。该系统使用数字0、1、2和3,用于表示实数[19]。QSD数字的有符号表示由以下给出,
$$
X=\sum_{i=-n}^{m} x_i \cdot 4^i
$$
其中,
十进制的正确表示由 $\overline{X}$ 生成。QSD正数的QSD补码产生QSD负数。例如,3= ‐3, 2= ‐2, 1= ‐1。通过恒定延迟,在数字实现中可实现128、256及更多数量的数字。QSD数制具有以下主要优点:减少互连和晶体管数量。系统的整体复杂度因此降低。该技术可用于实现乘法器和加法器,具有有效面积和速度优势。
2.2 通用逻辑门设计
二进制操作符类似于基本四进制操作符。它们通过布尔代数获得。基本操作符包括基本XNOR、基本NOR、基本NAND、基本反相器、与门、或门。
2.2.1 四进制反相器
在不同的逻辑电路中,四进制反相器起着重要作用。输入信号通过反相器功能进行取反。表1显示了四进制反相器的真值表。

表1:四进制逆变器真值表
| 输入 | 输出 |
|---|---|
| 0 | 3 |
| 1 | 2 |
| 2 | 1 |
| 3 | 0 |
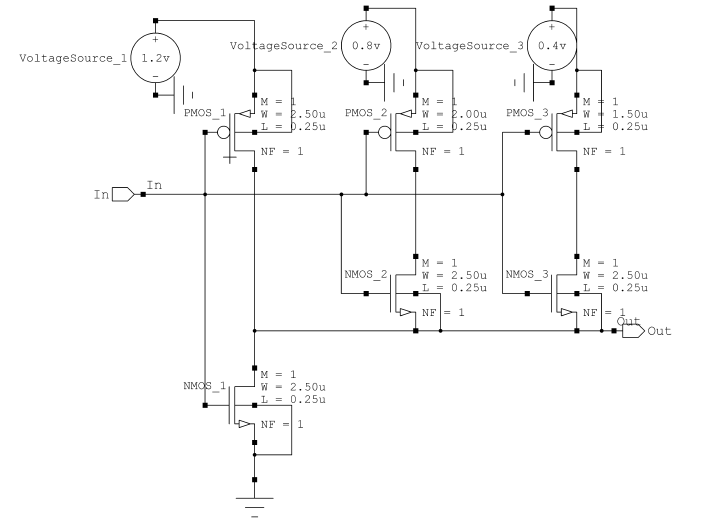
四进制反相器由六个晶体管组成,其中包含三个NMOS和三个PMOS,如图2所示。这些NMOS和PMOS在不同的阈值电压下工作。当输入值为0 V时,PMOS1导通,使输出为1.2 V,而NMOS1、NMOS2和NMOS3关闭,切断其余通路。
当输入值设为1V时,PMOS1关闭,而NMOS2导通,使输出为0.8 V。当输入值设为2V时,PMOS2关闭,而NMOS3导通,从而使输出降至0.4 V。只有当输入值设为3V时,PMOS3才关闭,NMOS1将输出拉低至零。
2.2.2 四进制NAND门
在不同的逻辑电路中,四进制NAND门起着重要作用。存储电路是使用…实现此。表2显示了四进制NAND门的真值表。
四进制NAND门的输出表示为,
$$
OUT = \overline{(A \cdot B)}
$$
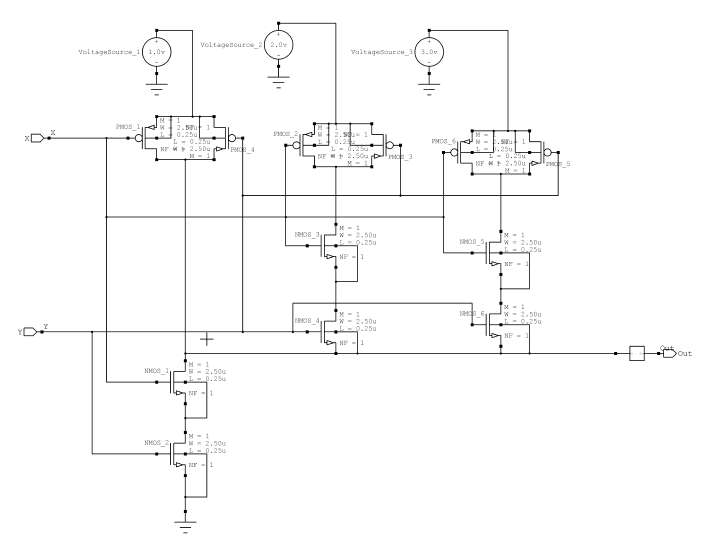
标准反相器定义了四进制NAND门的工作原理。与T1、T2、T3并联,增加了三个额外的晶体管。这些增加的晶体管接收第二个输入。标准反相器对应于阈值电压基本原理。图4显示了四进制NAND门的晶体管级电路图。
表2:四进制NAND门真值表
| In 1 | In 2 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| 0 | 3 | 3 | 3 | 3 | 3 |
| 1 | 3 | 2 | 2 | 2 | 2 |
| 2 | 3 | 2 | 1 | 1 | 1 |
| 3 | 3 | 2 | 1 | 0 | 0 |

2.2.3 四进制NOR门
使用四进制NOR门实现存储电路,如触发器。计数器和移位寄存器的实现基于这些触发器。图6显示了四进制NOR门的晶体管级电路图。
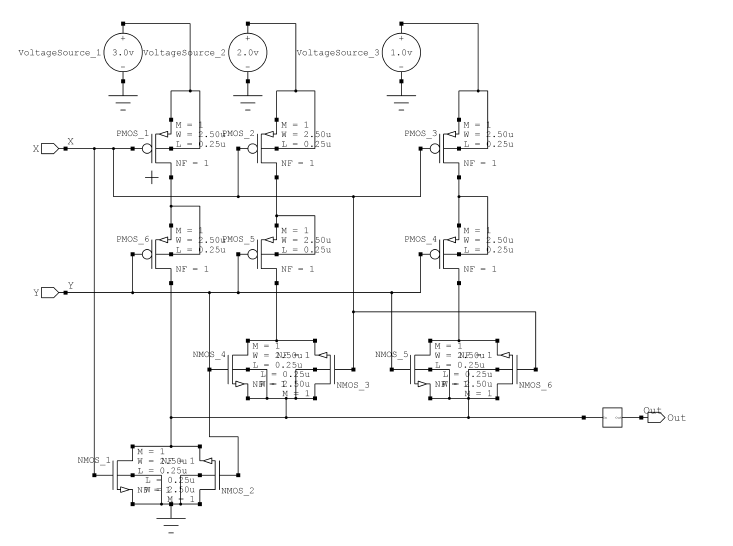
四进制NOR门的输出定义为,
$$
OUT = \overline{(In1 + In2)}
$$
表3:四进制NOR门真值表
| In 1 | In 2 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| 0 | 3 | 2 | 1 | 0 | 0 |
| 1 | 2 | 2 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 |
2.2 QSD加法器单元(半加器与全加器)
常见的算术电路对应于加法器。为了实现各种算术运算,它被用作基本单元。在大型加法器中,主要使用的基本单元是单比特全加器和半加器。各种类型的算术电路也通过这种方式构建。
A. 四进制半加器(QHA)的实现
两个输入X和Y作为输入提供给二进制半加器(HA)。该二进制半加器(HA)产生进位输出位C和和输出S。如图7所示。在四进制逻辑中,将两个四进制数字作为输入提供给半加器电路,并由该电路产生四进制进位和和数字。单数位四进制加法器对应于一个半加器。对于单数位输入,它产生两位和,即 $X + Y = (C, S)$。表4显示了四进制半加器真值表。
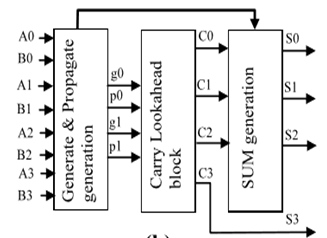
表4:四进制半加器真值表
| X | Y | Sum | 进位 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 2 | 2 | 0 |
| 0 | 3 | 3 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 2 | 0 |
| 1 | 2 | 3 | 0 |
| 1 | 3 | 0 | 1 |
| 2 | 0 | 2 | 0 |
| 2 | 1 | 3 | 0 |
| 2 | 2 | 0 | 1 |
| 2 | 3 | 1 | 1 |
| 3 | 0 | 3 | 0 |
| 3 | 1 | 0 | 1 |
| 3 | 2 | 1 | 1 |
| 3 | 3 | 2 | 1 |
B. 四进制全加器
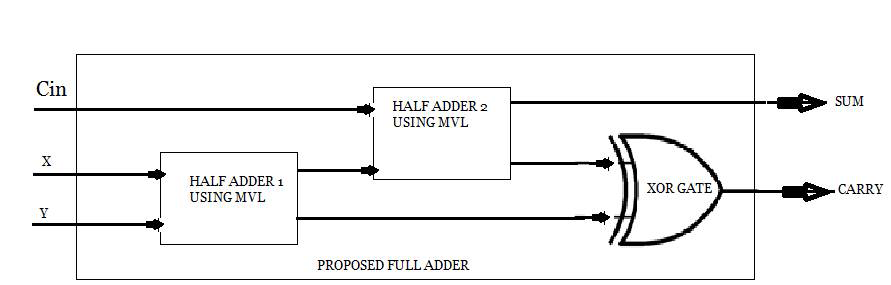
四进制半加器用于构建所提出的四进制全加器。进位输入Cin是该电路中增加的一个额外输入。该电路对四进制Cin数字和两个四进制数字进行加法运算。该电路生成四进制进位输出和和值。Cin引脚将仅有两个取值(0和1)。这一假设简化了电路的实现。四进制乘法器和加法器的实现方式非常有效。图8显示了四进制全加器的框图。
一个异或门和两个半加器用于构建四进制全加器。它类似于传统的全加器。两个四进制输入X和Y被送入第一个四进制半加器。第一个半加器的和与另一个输入C in 作为输入送入第二个四进制半加器。四进制全加器的和由第二个半加器的和输出产生。异或门的两个输入分别连接到第一个和第二个全加器的进位输出。所提出的全加法器的进位输出由该异或门的输出生成。表5显示了输入进位为0时全加器的真值表,表6显示了进位输入为1时全加器的真值表。
表5:当进位为= 0时的QFA真值表
| Cin | X | Y | Sum | 进位 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 2 | 2 | 0 |
| 0 | 0 | 3 | 3 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 2 | 0 |
| 0 | 1 | 2 | 3 | 0 |
| 0 | 1 | 3 | 0 | 1 |
| 0 | 2 | 0 | 2 | 0 |
| 0 | 2 | 1 | 3 | 0 |
| 0 | 2 | 2 | 0 | 1 |
| 0 | 2 | 3 | 1 | 1 |
| 0 | 3 | 0 | 3 | 0 |
| 0 | 3 | 1 | 0 | 1 |
| 0 | 3 | 2 | 1 | 1 |
| 0 | 3 | 3 | 2 | 1 |
表6:进位= 1时的四进制全加器真值表
| Cin | X | Y | Sum | 进位 |
|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 2 | 0 |
| 1 | 0 | 2 | 3 | 1 |
| 1 | 0 | 3 | 0 | 0 |
| 1 | 1 | 0 | 2 | 0 |
| 1 | 1 | 1 | 3 | 0 |
| 1 | 1 | 2 | 0 | 1 |
| 1 | 1 | 3 | 1 | 1 |
| 1 | 2 | 0 | 3 | 0 |
| 1 | 2 | 1 | 0 | 1 |
| 1 | 2 | 2 | 1 | 1 |
| 1 | 2 | 3 | 2 | 1 |
| 1 | 3 | 0 | 0 | 1 |
| 1 | 3 | 1 | 1 | 1 |
| 1 | 3 | 2 | 2 | 1 |
| 1 | 3 | 3 | 3 | 1 |
2.3 基于QSD的超前进位加法器
在加法器的架构中,通常使用超前进位加法器(CLA)架构。该架构中采用了进位生成和传播逻辑功能,表现出更优的性能。图9展示了这种加法器。通过最小化进位位持续时间,提升了CLA的速度。对于两个四进制数的每一位位置,在进行加法时会生成两个信号:生成和传播。图10显示了基于QSD的超前进位加法器的原理图。在CLA加法器中应用QSD逻辑,可提升阵列乘法器的性能。

2.4 使用基于QSD的超前进位加法器的乘法器
所有最新算法和应用都使用一种重要的算术电路,称为乘法器。阵列乘法器的规则结构使其广受欢迎。
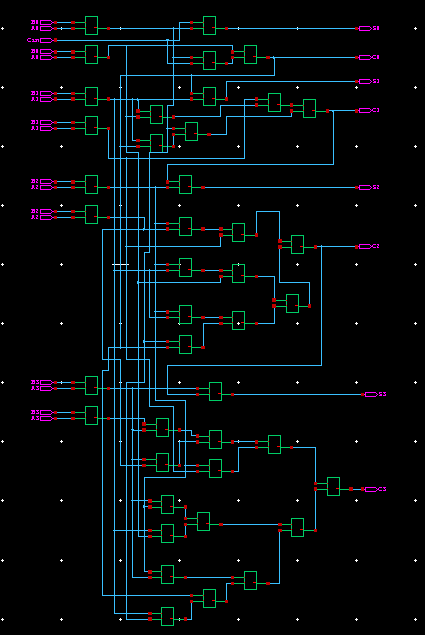
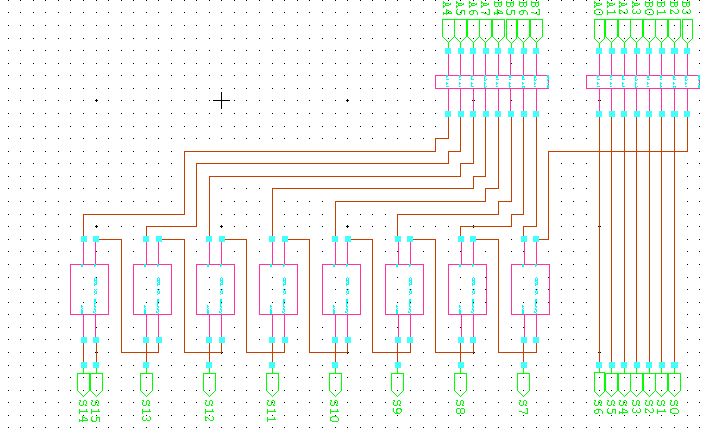
移位相加算法定义了乘法器电路。每一位乘数位与被乘数相乘产生每一个部分积。根据位序对这些部分积进行移位,然后进行计算加法。该加法运算使用普通进位传播加法器来完成。对于N长度乘法器,它需要N-1个加法器。在阵列乘法器架构中,使用基于QSD的超前进位加法器代替全加器。这是为了实现快速乘法,并降低功耗。图11展示了所提出的基于QSD的CLA结构乘法器的原理图。

3. 实验结果
使用Tanner EDA工具在180纳米技术下对提出的乘法器电路进行仿真。就面积、功耗延迟积(PDP)和平均功耗而言,所提出的QSD CLA乘法器与电源门控CLA和CLA乘法器进行了比较。
表7:性能比较
| 参数 | CLA乘法器 | 电源门控CLA | QSD CLA乘法器 |
|---|---|---|---|
| 平均功耗 | 12.81毫瓦 | 6.19毫瓦 | 0.21157微瓦(0.00021毫瓦) |
| 静态功耗 | 6.23毫瓦 | 5.21毫瓦 | 0.3485毫瓦 |
| PDP | 0.56075微瓦/秒 | 0.1806微瓦/秒 | 0.1742nw/s(0.0001742 uw/s) |
| 面积(晶体管数量) | 2484 | 2278 | 3392 |

图12显示了CLA乘法器、电源门控CLA和QSD CLA乘法器的平均功耗比较。x轴表示乘法器,y轴表示平均功耗。所提出的QSD CLA乘法器的平均功耗为0.00021毫瓦,而其他方法如CLA乘法器、电源门控CLA乘法器的平均功耗分别为12.81毫瓦和6.19毫瓦。从结果可以看出,所提出的乘法器相比其他乘法器实现了最低的平均功耗。
CLA乘法器、电源门控CLA和QSD CLA乘法器的比较是基于静态功耗进行的。x轴表示乘法器,y轴表示静态功耗。根据仿真结果可以得出,所提出的乘法器实现了0.3485毫瓦的静态功耗,而其他方法如CLA乘法器和电源门控CLA分别达到6.23毫瓦和5.21毫瓦。与其他乘法器相比,所提出的乘法器实现了最低的静态功耗。
CLA乘法器、电源门控CLA和QSD CLA乘法器在功耗延迟积方面进行了比较。乘法器的PDP比较如图14所示。x轴为乘法器,y轴为PDP。根据实验结果可以得出,所设计的乘法器实现了0.0001742 微瓦/秒的PDP,而其他乘法器如CLA乘法器、电源门控CLA分别达到0.56075微瓦/秒和0.1806微瓦/秒。
图15显示了CLA乘法器、电源门控CLA和QSD CLA乘法器的面积比较。在x轴上为乘法器,面积作为y轴。提出的乘法器电路的面积为3392,而其他方法如CLA乘法器和电源门控CLA乘法器的面积分别为2484和2278。
4. 结论
基于QSD的超前进位加法器在本设计中用于阵列乘法器的设计。它是一种高速且低功耗的器件。QSD数制消除了进位传播链。加法器速度通过该设计,性能得到提升,系统的计算时间减少。在乘法器电路中,基于QSD的阵列乘法器结合CLA加法器提升了性能。使用Tanner EDA工具在180纳米技术下对提出的乘法器电路进行仿真。
在面积、功耗延迟积(PDP)和平均功耗方面,所提出的QSD CLA乘法器与电源门控CLA和CLA乘法器进行了比较。分析结果表明,与CLA乘法器和电源门控CLA相比,QSD CLA乘法器所需的面积较大,但在平均功耗和PDP性能方面优于CLA乘法器和电源门控CLA乘法器。未来,该设计适用于构建由多个处理单元组成的高性能多处理器。




















 3910
3910

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








