在Unity Shader中,CG提供了一些内建的标准函数。这些函数用于执行数学上的通用计算或通用算法(纹理映射等), 有些函数直接和 GPU 指令相对应,所以执行效率非常高,主要分为数学函数、几何函数、纹理映射函数、偏导函数、调试函数。
数学函数
这些数学函数用于执行数学上常用的计算,包括三角函数、幂函数、园函数、向量和矩阵的操作函数,这些函数都被重载,以支持标量数据和不同长度的向量作为输入函数。 • abs(x) //返回输入参数的绝对值
• acos(x) //反余切函数,输入参数范围为[-1,1],返回[0,π]区间的角度值
• all(x) //如果输入参数均不为0,则返回 ture;否则返回 flase。&&运算
• any(x) //输入参数只要有其中一个不为0,则返回 true。||运算
• asin(x) //反正弦函数,输入参数取值区间为[−1,1],返回角度值范围为[−π/2 ,π/2 ]
• atan(x) //反正切函数,返回角度值范围为⎡−π/2 ,π/2⎤
• atan2(y,x) //计算y/x 的反正切值。实际上和atan(x)函数功能完全一样,至少输入参数不同。 atan(x) = atan2(x, float(1))
• ceil(x) //对输入参数向上取整。例如:ceil(float(1.3)),其返回值为 2.0
• clamp(x,a,b) //如果x 值小于 a,则返回a;如果 x 值大于 b,返回b;否则,返回 x
• cos(x) //返回弧度 x 的余弦值。返回值范围为[−1,1]
• cross(A,B) //返回两个三元向量的叉积(cross product)。注意,输入参数必须是三元向量
• degrees(x) //输入参数为弧度值(radians),函数将其转换为角度值(degrees)
• determinant(m) //计算矩阵的行列式因子
• dot(A,B) //返回A 和 B的点积(dot product)。参数A 和 B 可以是标量,也可以是向量(输入参数方面,点积和叉积函数有很大不同)
• exp(x) //计算ex的值,e= 2.71828182845904523536
• exp2(x) //计算2x的值
• floor(x) //对输入参数向下取整。例如floor(float(1.3)) 返回的值为1.0;但是 floor(float(-1.3))返回的值为-2.0。
• fmod(x,y) //返回x/y 的余数。如果 y 为 0,结果不可预料
• frexp(x, out exp) //将浮点数 x 分解为尾数和指数,即x = m* 2^exp,返回m,并将指数存入 exp 中;如果 x 为 0,则尾数和指数都返回0
• frac(x) //Returns the fractional portion of a scalar or each vector component
• isfinite(x) //判断标量或者向量中的每个数据是否是有限数,如果是返回true;否则返回false;无限的或者非数据(not-a-number NaN)
• isinf(x) //判断标量或者向量中的每个数据是否是无限,如果是返回 true;否则返回 false;
• isnan(x) //判断标量或者向量中的每个数据是否是非数据(not-a-number NaN),如果是返回true;否则返回false;
• ldexp(x, n) //计算x∗2n的值
• lerp(a, b, f) //计算(1−f )∗ + ∗a b f或者a+f ∗ −(b a)的值。即在下限a 和上限 b 之间进行插值,f表示权值。注意,如果 a和 b 是向量,则权值 f必须是标量或者等长的向量。
• lit(NdotL,NdotH, m) /N表示法向量;L 表示入射光向量;H表示半角向量;m 表示高光系数。函数计算环境光、散射光、镜面光的贡献,返回的 4元向量: X.位表示环境光的贡献,总是 1.0; Y.位代表镜面光的贡献,如果 N •L<0,则为0;否则为 N •L; Z.位代表镜面光的贡献,如果N •L<0或者 N •H <0 ,则位 0;否则为(N •H)m; W位始终位 1.0 /
• log(x) //计算ln(x)的值,x必须大于 0
• log2(x) //计算log(2x)的值,x 必须大于 0
• log10(x) //计算log10(x)的值,x必须大于 0
• max(a, b) //比较两个标量或等长向量元素,返回 大值
• min(a,b) //比较两个标量或等长向量元素,返回 小值
• step(a, x) //如果 x<a,返回0;否则,返回1。
• sqrt(x) //求 x的平方根, x ,x必须大于 0。
• tan(x) //输入参数为弧度,计算正切值
• transpose(M) //M 为矩阵,计算其转置矩阵
• mul(M, N) //计算两个矩阵相乘,如果 M 为 AxB 阶矩阵,N 为 BxC阶矩阵,则返回 AxC 阶矩阵。下面两个函数为其重载函数。
• mul(M, v) //计算矩阵和向量相乘
• mul(v, M) //计算向量和矩阵相乘
• noise( x) // 噪声函数,返回值始终在 0,1 之间;对于同样的输入,始终返回相同的值(也就是说,并不是真正意义上的随机噪声)。
• pow(x, y) //计算x的y次幂,y为2时是x的平方,y为3时是x的立方,依次类推。
• radians(x) //函数将角度值转换为弧度值
• round(x) //Round-to-nearest,或 closest integer to x 即四舍五入
• rsqrt(x) // X 的反平方根,x 必须大于 0
• saturate(x) //如果 x 小于 0,返回 0;如果 x 大于 1,返回1;否则,返回 x
• sign(x) //如果 x 大于 0,返回 1;如果 x 小于 0,返回01;否则返回 0。
• sin(x) //输入参数为弧度,计算正弦值,返回值范围为[−1,1]
• sincos(float x, out s, out c) //该函数是同时计算 x 的 sin 值和 cos 值,其中s=sin(x),c=cos(x)。该函数用于“同时需要计算 sin 值和 cos 值的情况”,比分别运算要快很多!
• sinh(x) //计算双曲正弦(hyperbolic sine)值。
• smoothstep(min, max, x) //值 x 位于 min、max 区间中。如果 x=min,返回 0;如果 x=max,返回 1。
几何函数
用于执行和解析几何相关的计算,例如根据入射光向量和顶点法向量求反射光和折射方向向量。有两点需要注意:1在着色程序中的向量最好进行归一化后再使用;2reflect函数和refract函数都存在以“入射光方向向量”作为输入参数,这两个函数中使用的入射光方向向量是从外指向几何顶点的。平时我们在着色程序中或者课本上都是将入射光方向向量作为顶点出发。 • distance( pt1, pt2) //两点之间的欧几里德距离(Euclidean distance)
• faceforward(N,I,Ng) //如果Ng I• <0 ,返回N;否则返回-N。
• length(v) //返回一个向量的模,即 sqrt(dot(v,v))
• normalize( v) //归一化向量
• reflect(I, N) //根据入射光方向向量 I,和顶点法向量N,计算反射光方向向量。其中I和N 必须被归一化,需要非常注意的是,这个I 是指向顶点的;函数只对三元向量有效。
• refract(I,N,eta) //计算折射向量,I为入射光线,N为法向量,eta为折射系数;其中 I 和N必须被归一化,如果I 和N 之间的夹角太大,则返回(0,0,0),也就是没有折射光线;I是指向顶点的;函数只对三元向量有效。
纹理映射函数
• tex1D(sampler1D tex, float s) // 一维纹理查询
• tex1D(sampler1D tex, float s, float dsdx, float dsdy) // 使用导数值(derivatives)查询一维纹理
• Tex1D(sampler1D tex, float2 sz) // 一维纹理查询,并进行深度值比较
• Tex1D(sampler1D tex, float2 sz, float dsdx,float dsdy) //使用导数值(derivatives)查询一维纹理, 并进行深度值比较
• Tex1Dproj(sampler1D tex, float2 sq) //一维投影纹理查询
• Tex1Dproj(sampler1D tex, float3 szq) //一维投影纹理查询,并比较深度值
• Tex2D(sampler2D tex, float2 s) //二维纹理查询
• Tex2D(sampler2D tex, float2 s, float2 dsdx, float2 dsdy) //使用导数值(derivatives)查询二维纹理
• Tex2D(sampler2D tex, float3 sz) //二维纹理查询,并进行深度值比较
• Tex2D(sampler2D tex, float3 sz, float2 dsdx,float2 dsdy) //使用导数值(derivatives)查询二维纹理,并进行深度值比较
• Tex2Dproj(sampler2D tex, float3 sq) //二维投影纹理查询
• Tex2Dproj(sampler2D tex, float4 szq) //二维投影纹理查询,并进行深度值比较 texRECT(samplerRECT tex, float2 s)
• texRECT (samplerRECT tex, float2 s, float2 dsdx, float2 dsdy)
texRECT (samplerRECT tex, float3 sz) texRECT (samplerRECT tex, float3 sz, float2 dsdx,float2 dsdy) texRECT proj(samplerRECT tex, float3 sq) texRECT proj(samplerRECT tex, float3 szq)
• Tex3D(sampler3D tex, float s) // 三维纹理查询
• Tex3D(sampler3D tex, float3 s, float3 dsdx, float3 dsdy) //结合导数值(derivatives)查询三维纹理
• Tex3Dproj(sampler3D tex, float4 szq) //查询三维投影纹理,并进行深度值比较
• texCUBE(samplerCUBE tex, float3 s) //查询立方体纹理
• texCUBE (samplerCUBE tex, float3 s, float3 dsdx, float3 dsdy) //结合导数值(derivatives)查询立方体纹理
• texCUBEproj (samplerCUBE tex, float4 sq) //查询投影立方体纹理
s 象征一元、二元、三元纹理坐标;z 代表使用“深度比较(depth comparison)” 的值;q 表示一个透视值(perspective value,其实就是透视投影后所得到的齐次坐标的 后一位),这个值被用来除以纹理坐标(S),得到新的纹理坐标(已归一化到 0 和 1 之间)然后用于纹理查询。 纹理函数非常多,总的来说,按照纹理维数进行分类,即:1D 纹理函数, 2D 纹理函数,3D 纹理函数,已经立方体纹理。需要注意,TexREC 函数查询的纹理实际上也是二维纹理。 3D 纹理,另一个比较学术化的名称是“体纹理(Volume Texture)”,体纹理通常用于体绘制,体纹理用于记录空间中的体细节数据。 还有一类较为特殊的纹理查询函数以 proj 结尾,主要是针对投影纹理进行查询。所谓投影纹理是指:将纹理当做一张幻灯片投影到场景中,使用投影纹理技术需要计算投影纹理坐标,然后使用投影纹理坐标进行查询。使用投影纹理坐标进行查询的函数就是投影纹理查询函数。 本质来说,投影纹理查询函数和普通的纹理查询函数没有什么不同,唯一的区别在于“投影纹理查询函数使用计算得到的投影纹理坐标,并在使用之前会将该投影纹理坐标除以透视值”。举例而言,计算得到的投影纹理坐标为 float4 uvproj,使用二维投影纹理查询函数: tex2Dproj(texture,uvproj); 等价于按如下方法使用普通二维纹理查询函数:float4 uvproj = uvproj/uvproj.q; tex2D(texture,uvproj);
偏导函数
偏导数的物理含义是:在某一个方向上的变化快慢。所以 ddx 求的是 X 方向上,相邻两个像素的某属性值的变化量;ddy 求的是 Y 方向上,相邻两个像素的某属性值的变化量,如果函数 ddx 和 ddy 的输 入参数为常数,则函数返回值永远为 0。
• ddx(a) // 参数 a 对应一个像素位置,返回该像素值在 X 轴上的偏导数
• ddy(a) //参数 a 对应一个像素位置,返回该像素值在 X 轴上的偏导数
调试函数
• void debug(float4 x) //如果在编译时设置了DEBUG,片段着色程序中调用该函数可以将值X作为COLOR语义的最终输出,否则该函数什么也不做。
以上函数其实说多不多说少不少,不需要一次全部都记下来,用到的时候再来查询,多写几次自然就记住了,在这里整理出来一方面是自己留点印象,另外一方面也是方面以后使用查询。
=================================================================================
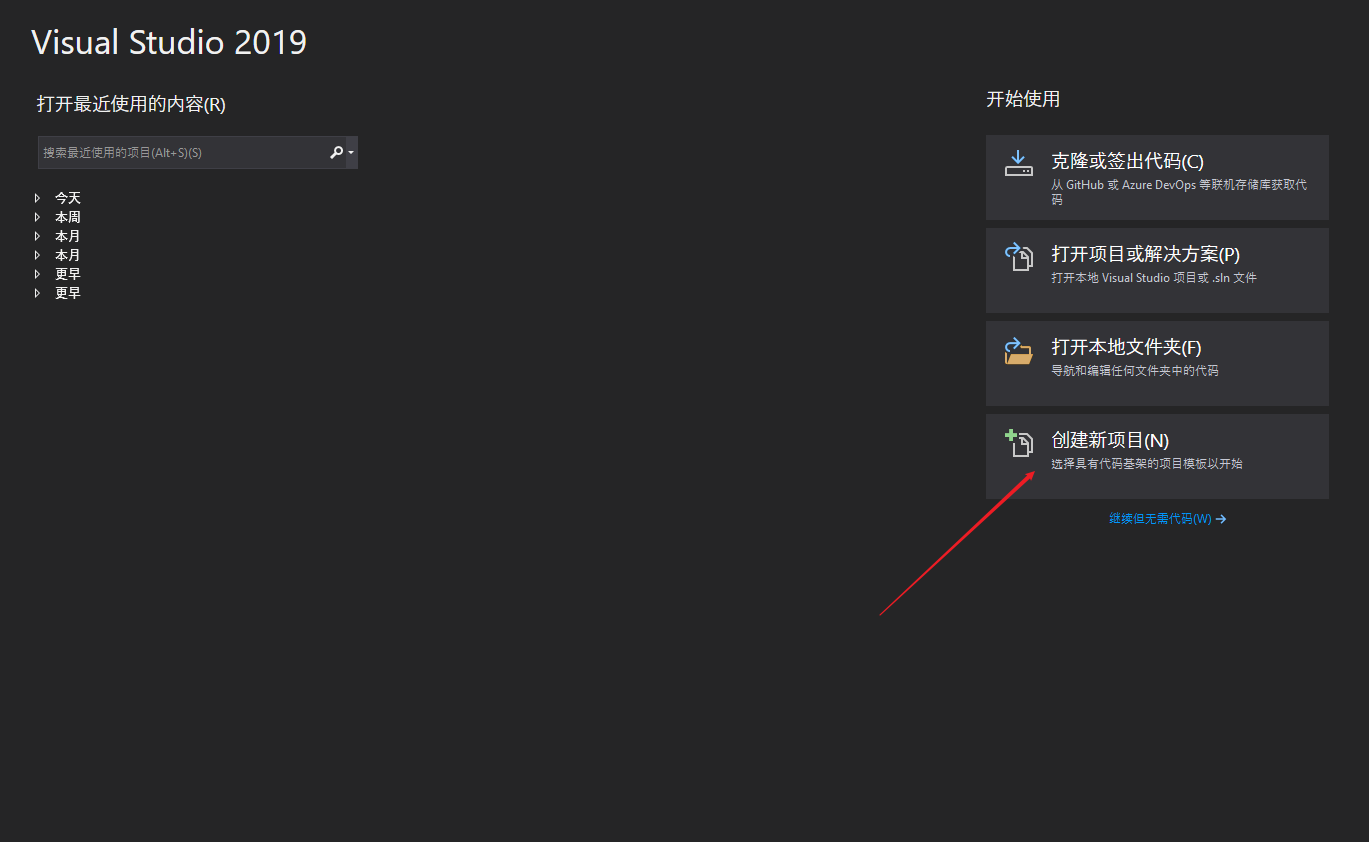
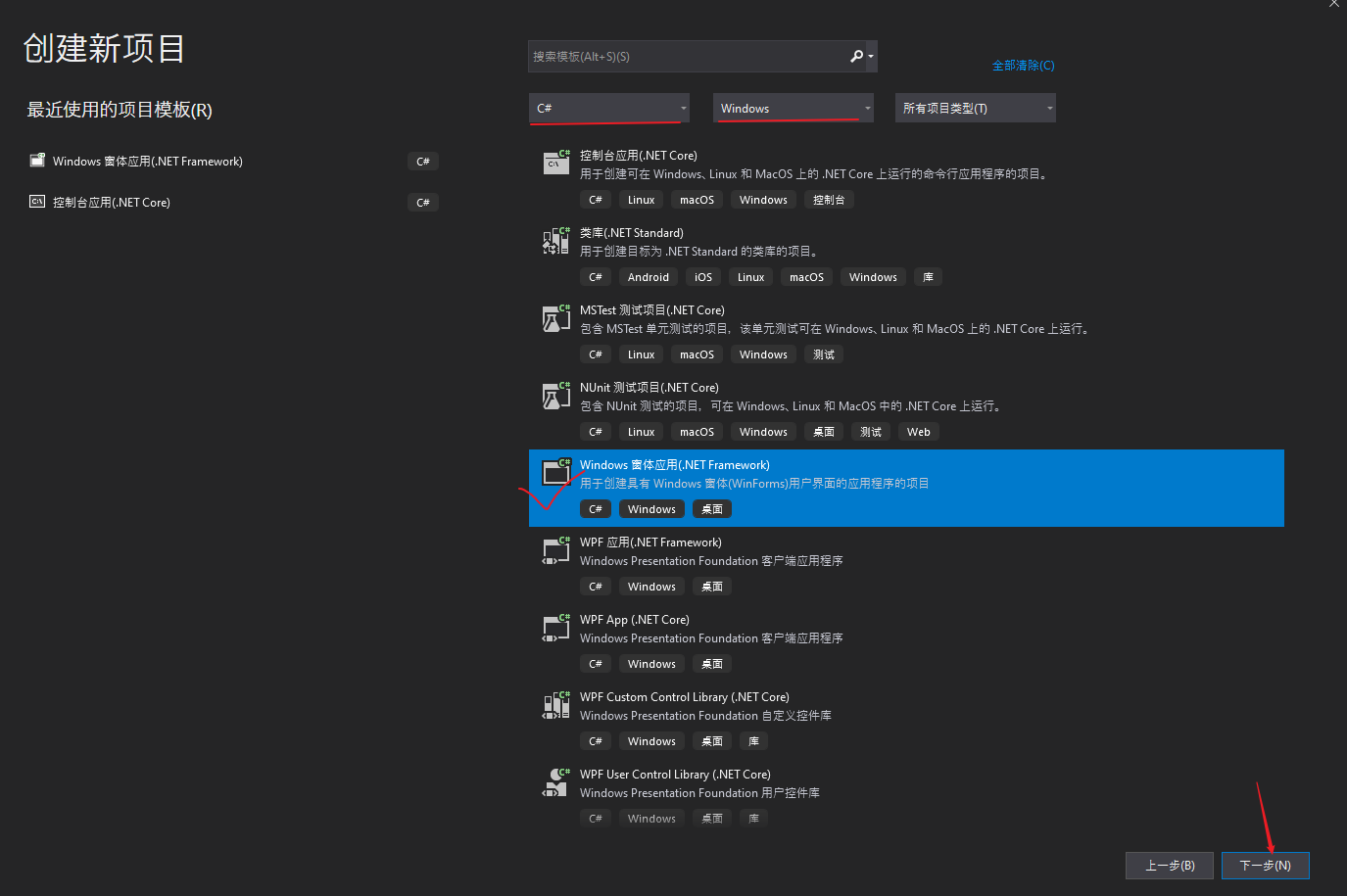
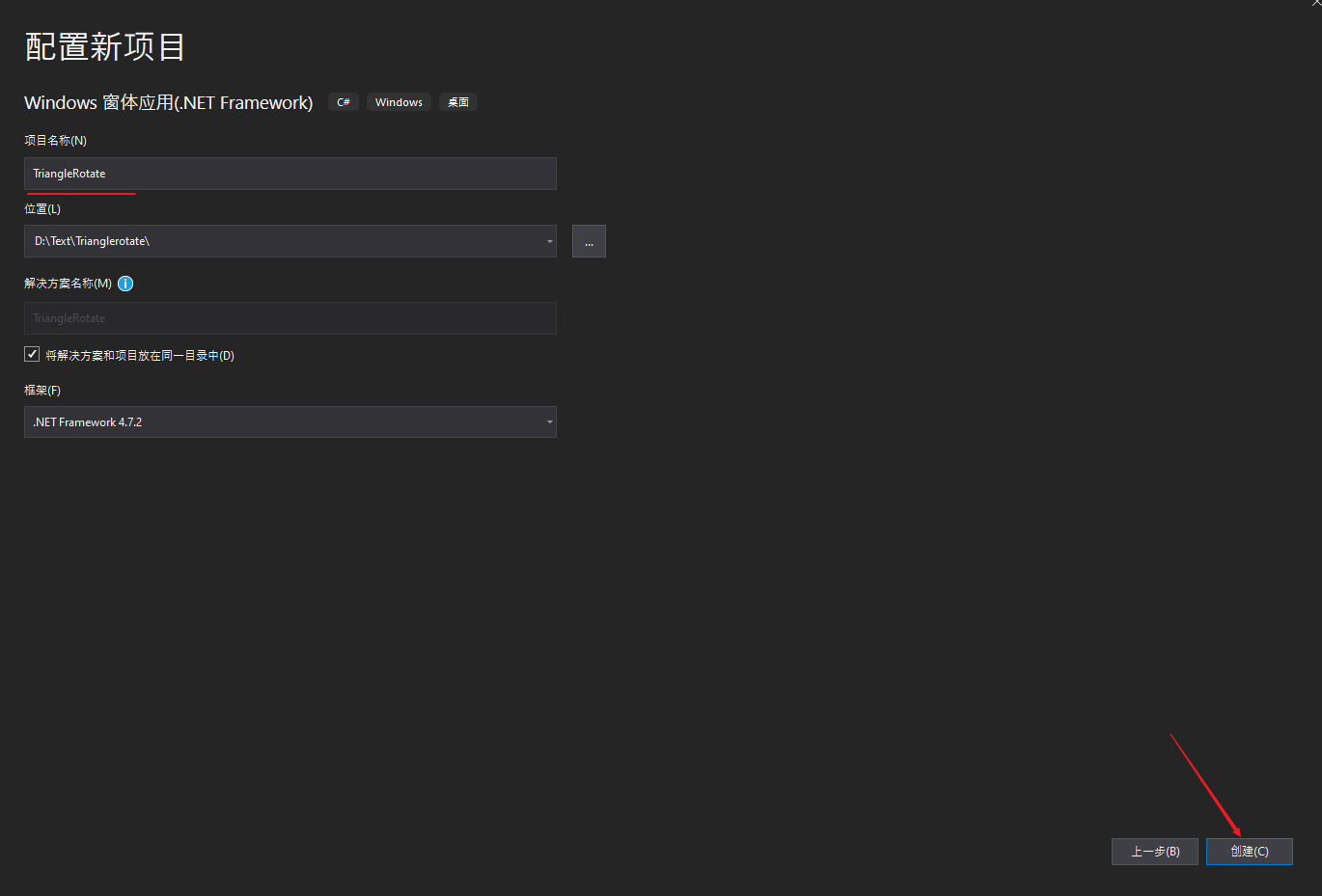
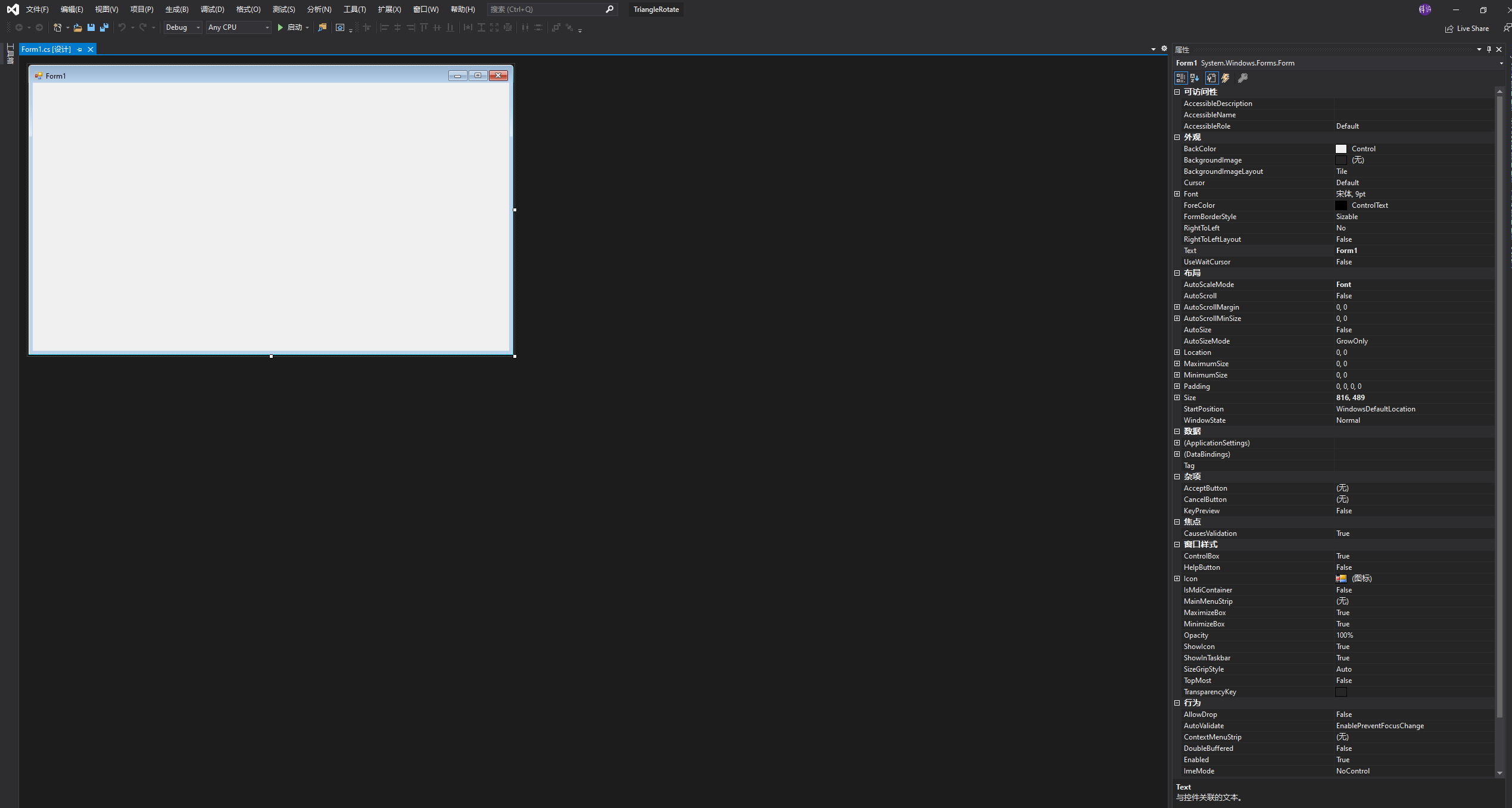
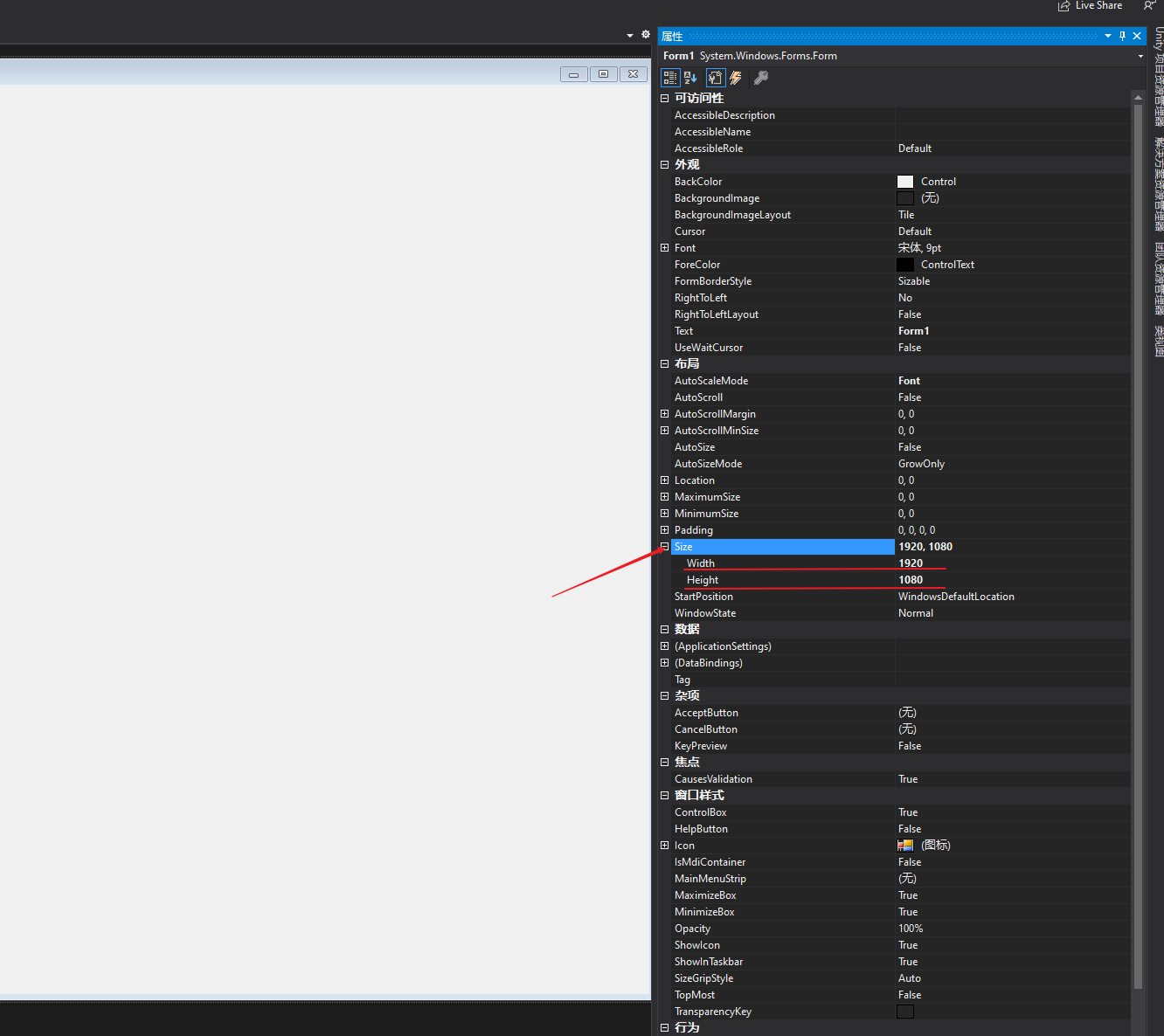
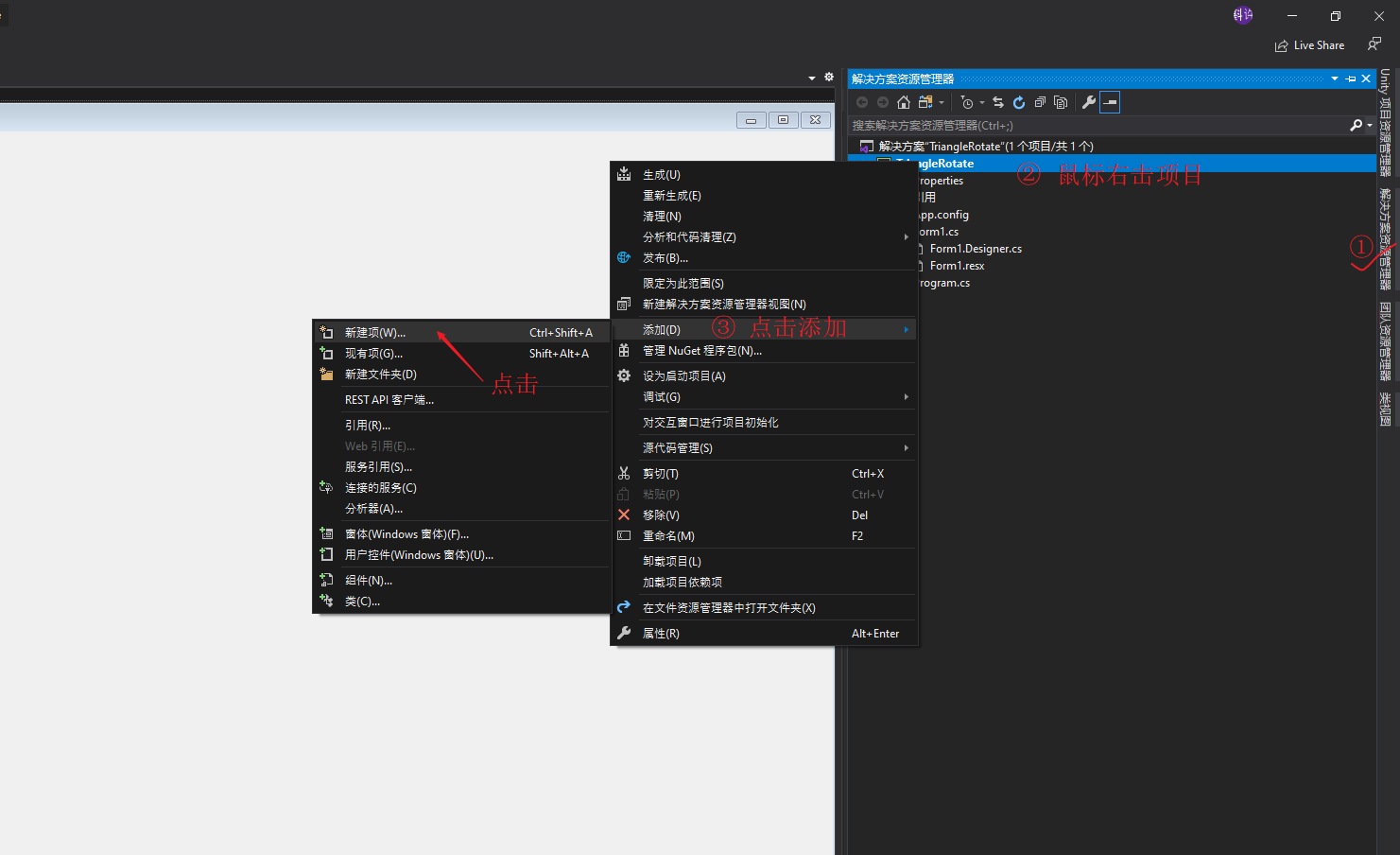
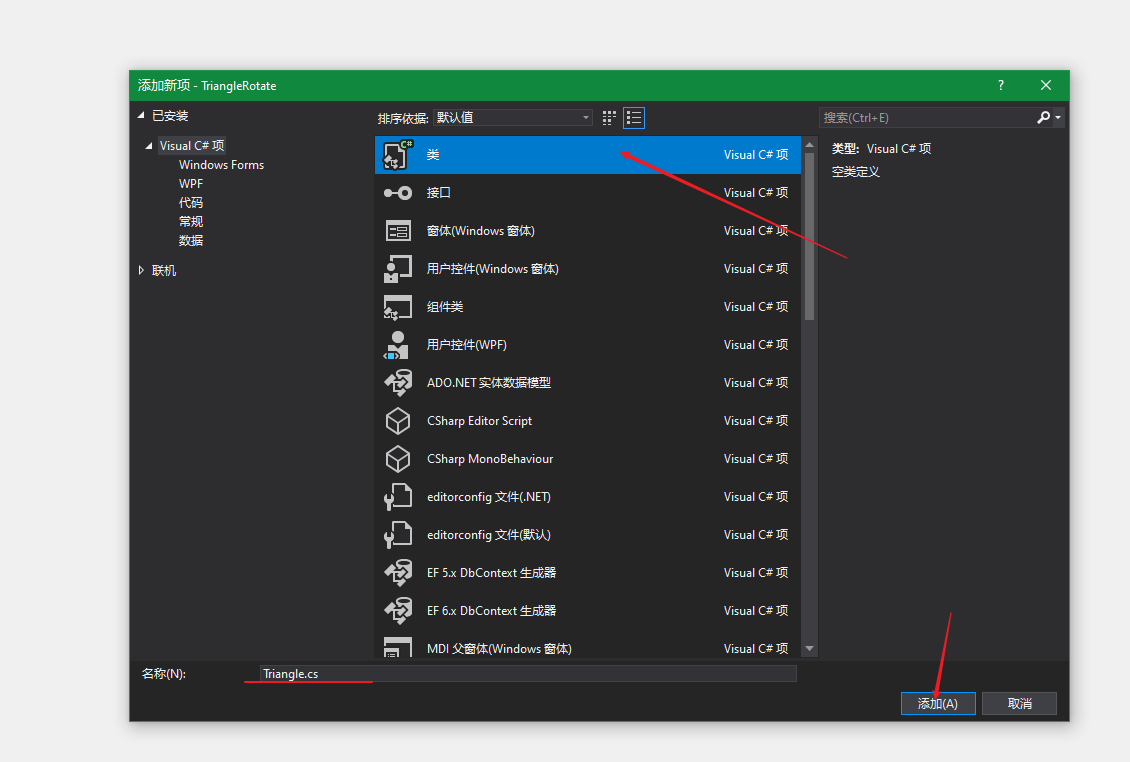
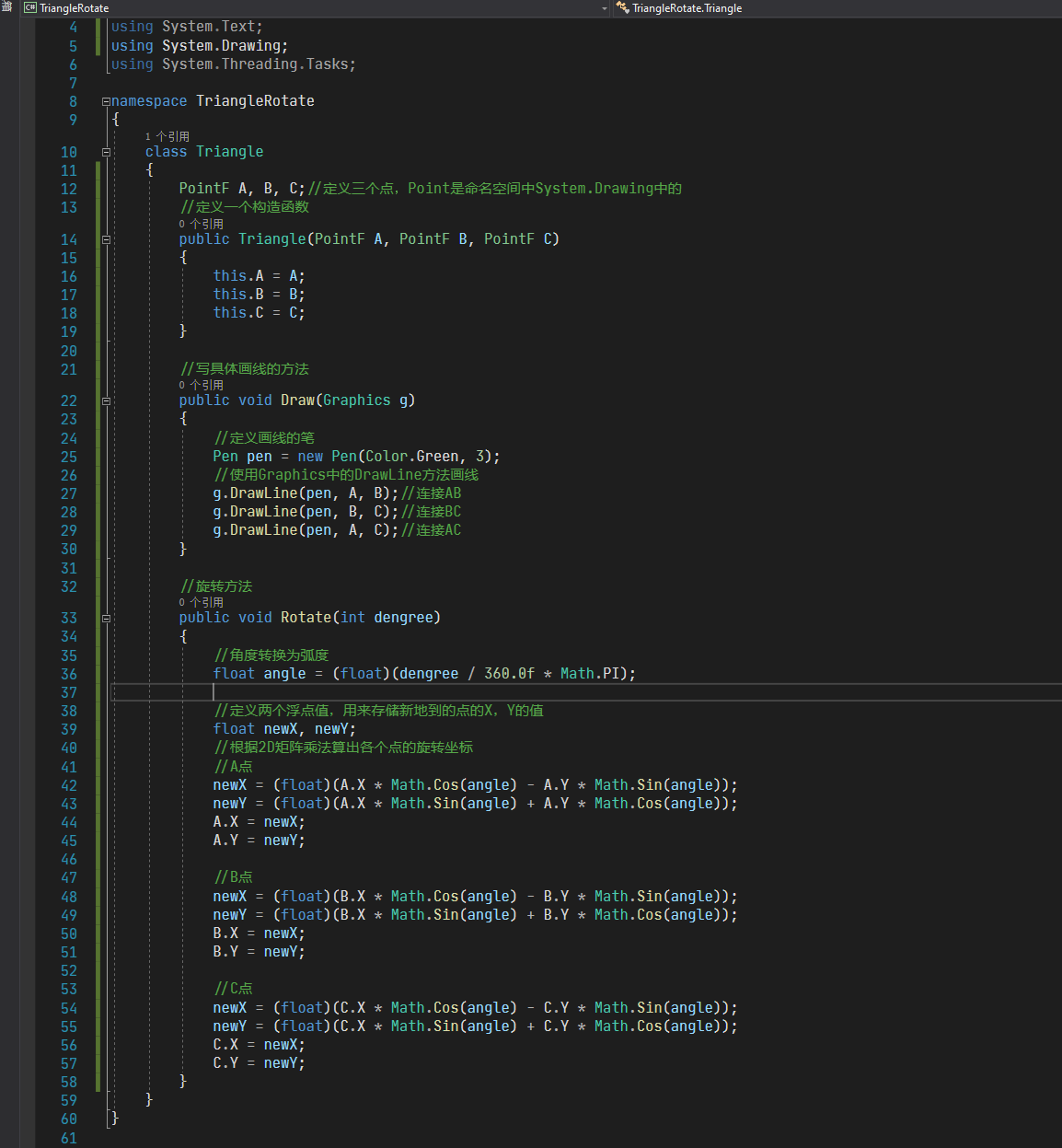
接下来要使用Windows窗口程序写一些代码,用三个点画一个三角形,之后使用2D旋转矩阵对点的位置进行变换,最终实现三角形绕中心旋转的效果。之所以是用Windows窗口程序是因为要绕开Unity纯粹的去体会矩阵对点变换的作用,以后写shader代码就直接用矩阵不用在刻意说明,这里就只用2D旋转矩阵举个栗子。 先列出2D旋转矩阵: 之后我们打开Visual Studio,估计现在很多是用2017,我这里体验就用的2019,基本流程不差,我们新建一个项目,如下图: 点击创建项目之后跳转页面,有几个注意的点,用红线标注了,之后点击下一步如下图: 之后我们填写项目名称,修改保存位置,之后点创建: 之后不出意外是如下图的样子: 之后我们找到属性列表,将Size属性的值更改一下,这里改为1920*1080,这样窗口就大一些,如下图: 之后,打开解决方案资源管理器(想要回到属性面板,点击窗口中的空白窗口即可),选中项目鼠标右击选择添加->新建项,如下图: 之后出现新建窗口,选择类,命名为Triangle,之后点击添加,如下图: 之后我们在脚本中引入using System.Drawing,写上代码,如下图: 这时不用在意代码是否优美,简单粗暴好理解即可。我们要在窗口中划线,那么我们就用窗口事件中的Paint事件,如下图: 这时,我们还需要一步操作,在事件中找到Load,双击它添加一个事件,在此之后我们还需要添加一个Timer工具,来使绘制的三角形按一定时间旋转,点击工具箱添加Timer,如下图: 之后要在Timer的窗口属性中设置一下,如下图: 之后,我们回到Form1脚本下,可以看到已经添加了Paint和Load以及Timer的事件,我们写入代码,如下图: 这里要插入说明一下,如下图: 之后,我们还需要回到窗口属性,将DoubleBuffer属性改为True,之后我们运行则可以看到窗口中的三角形在窗口中心旋转,如下图:

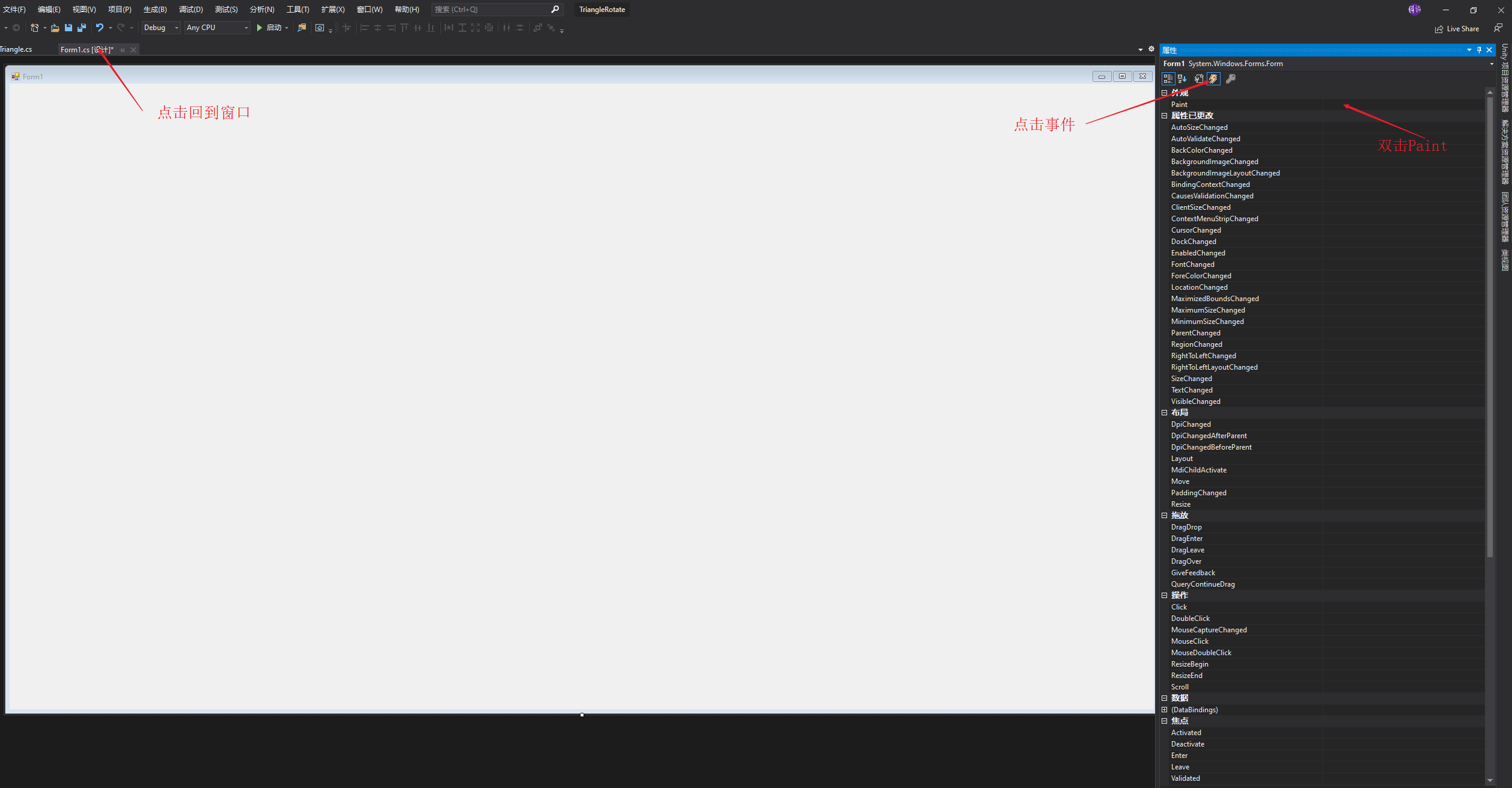
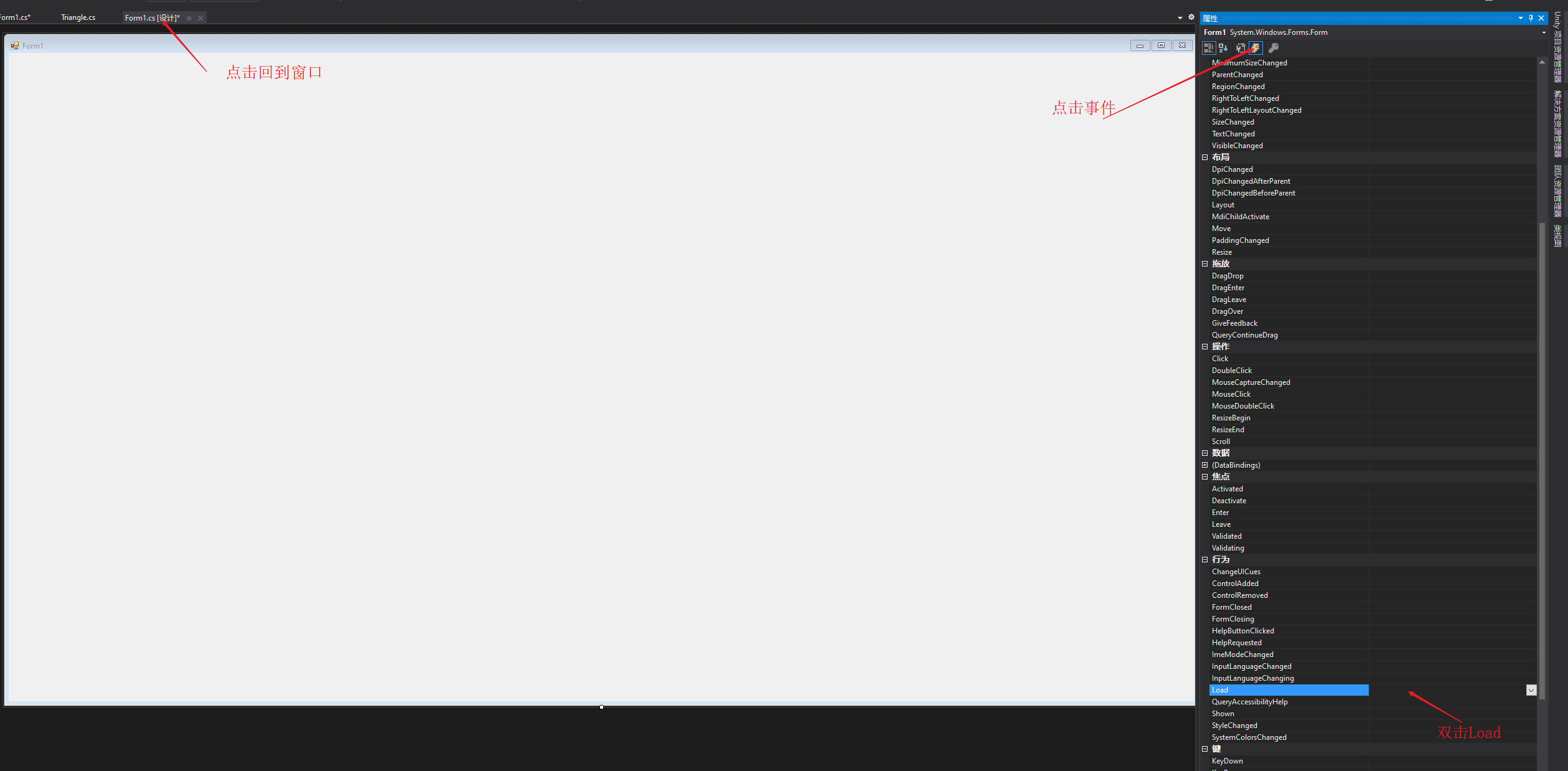
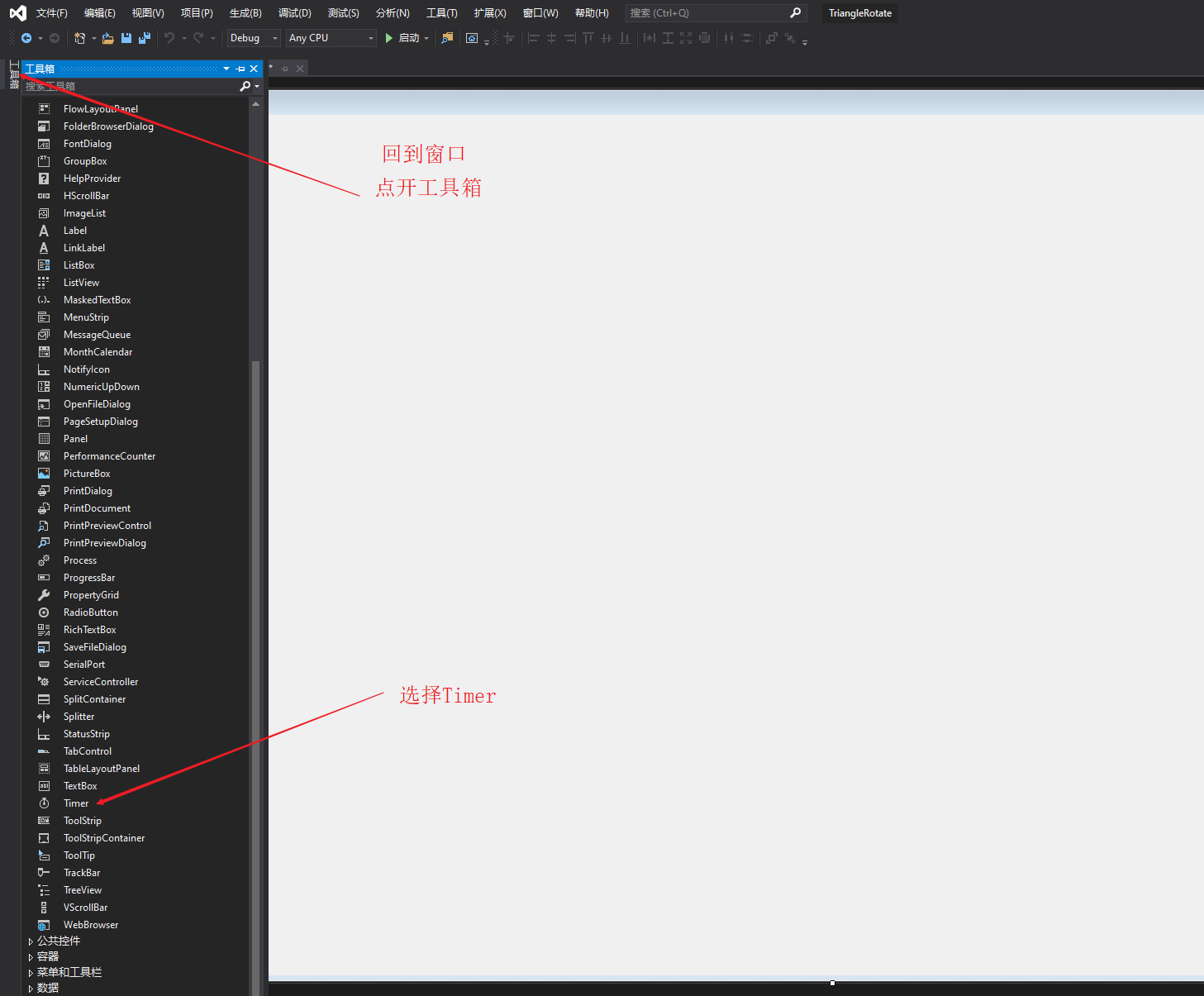
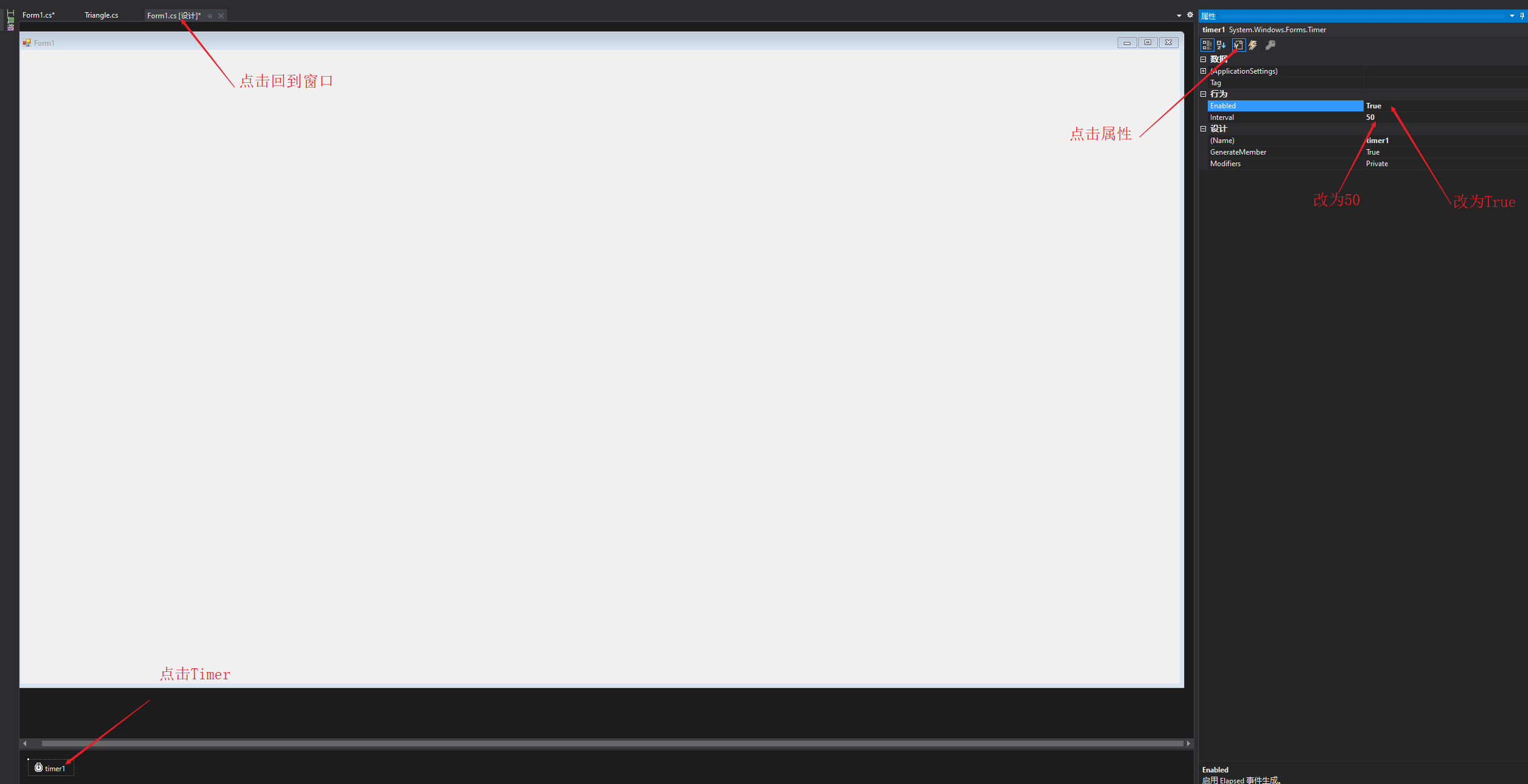
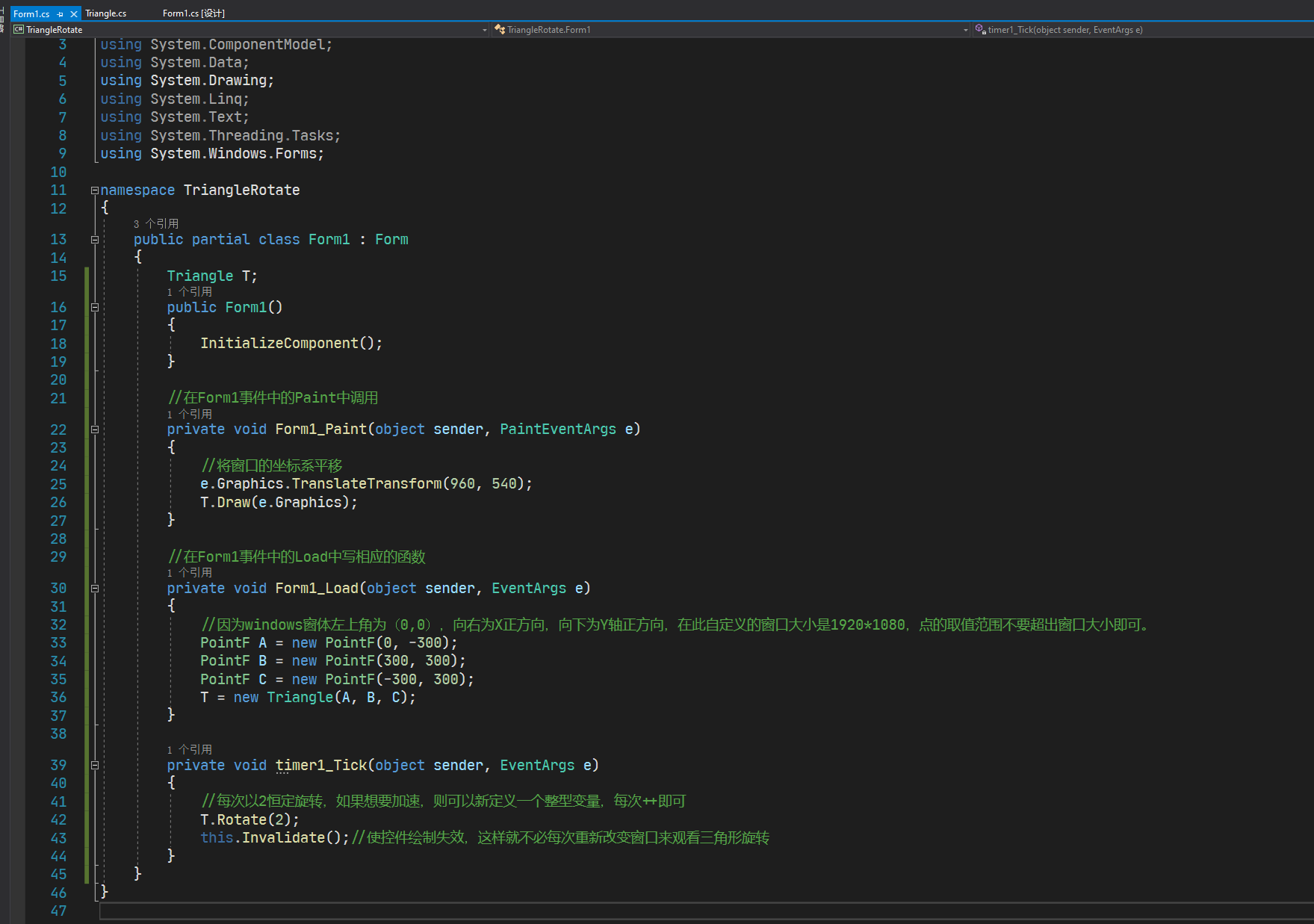
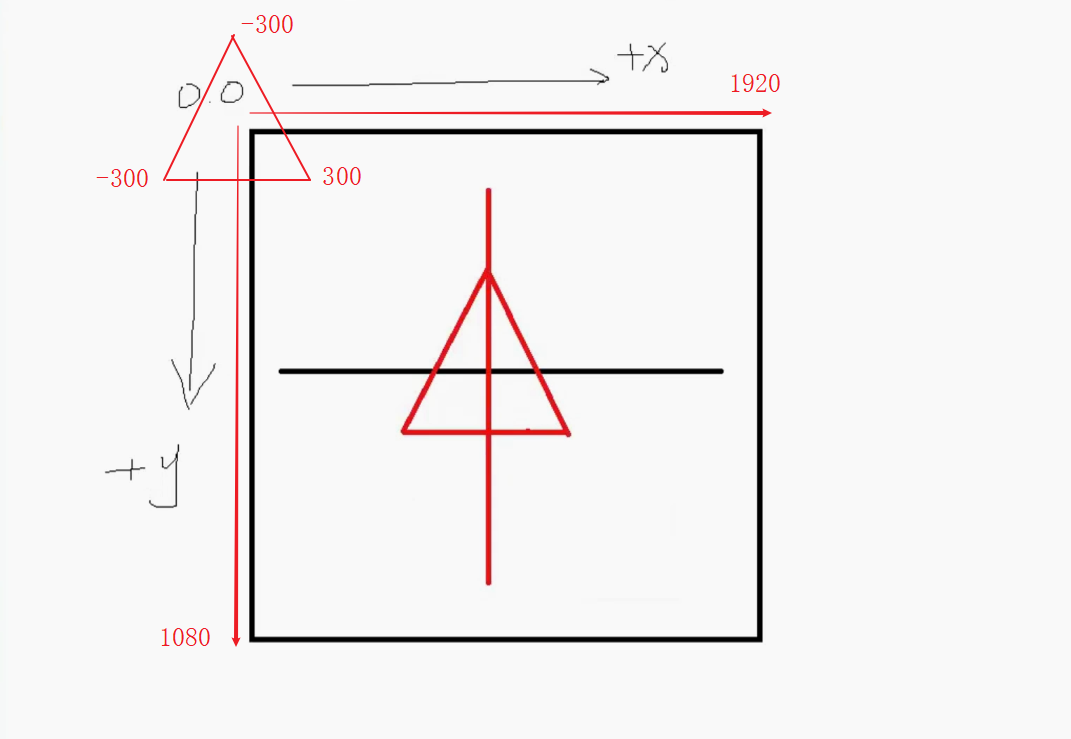
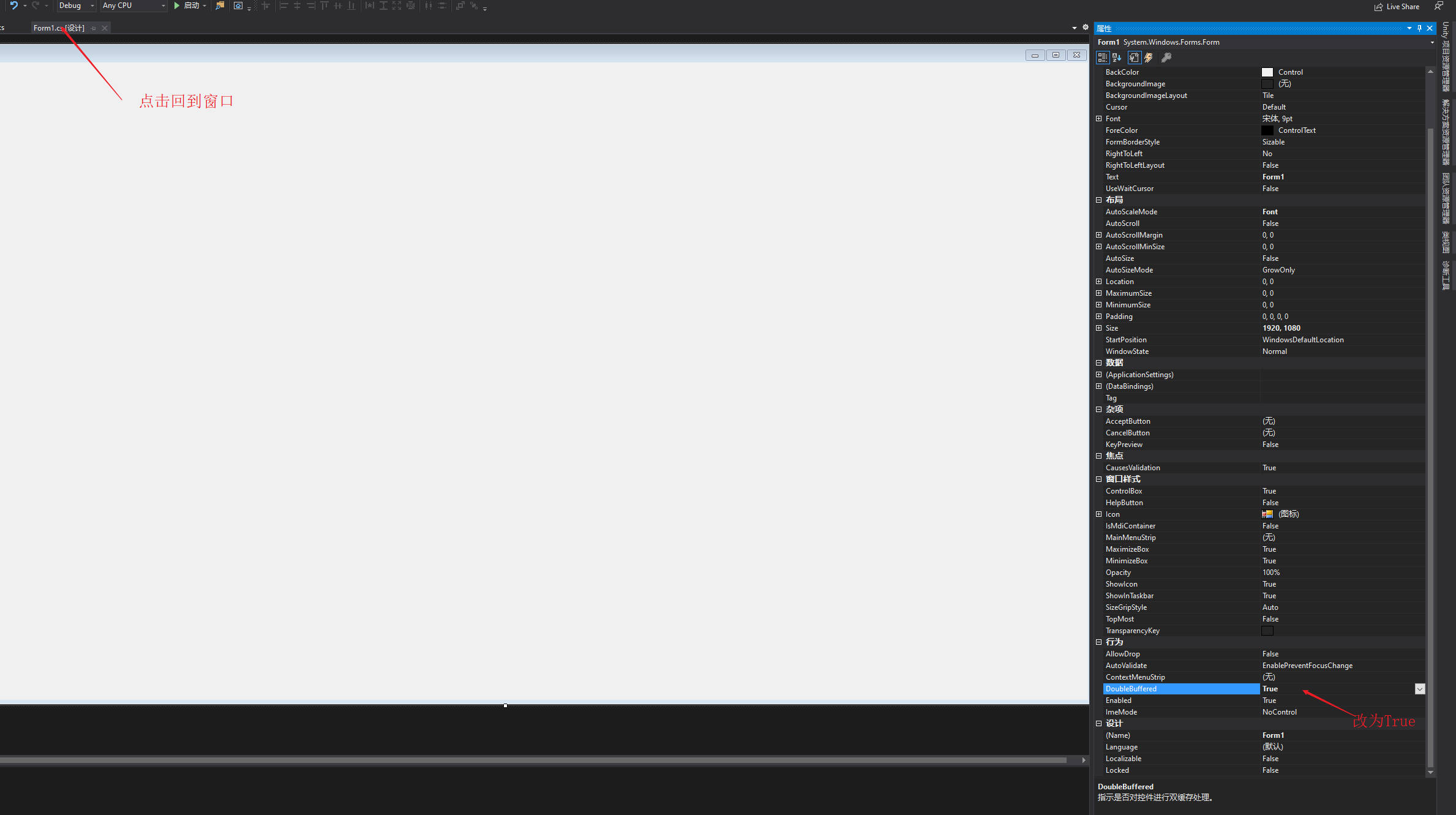
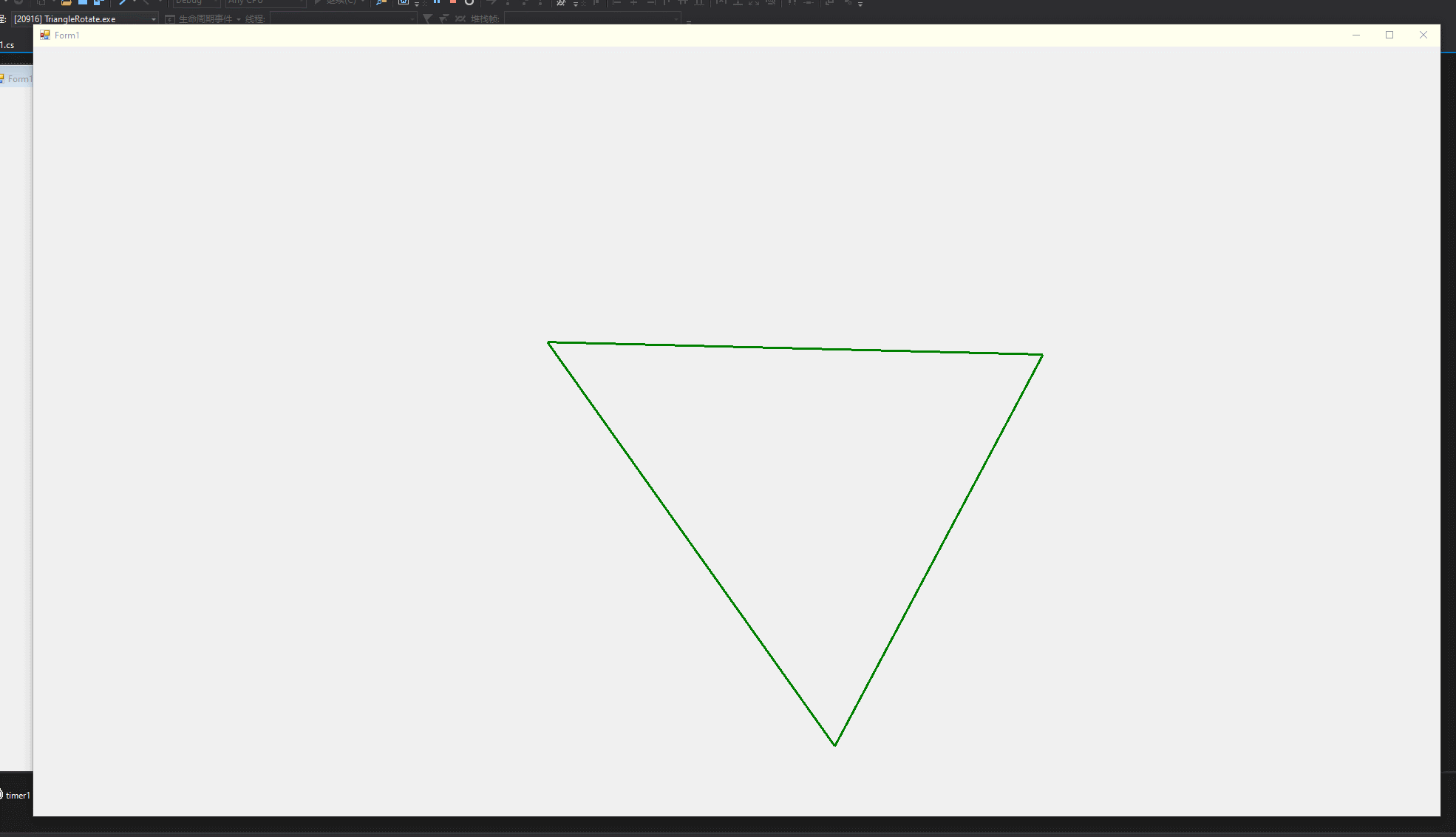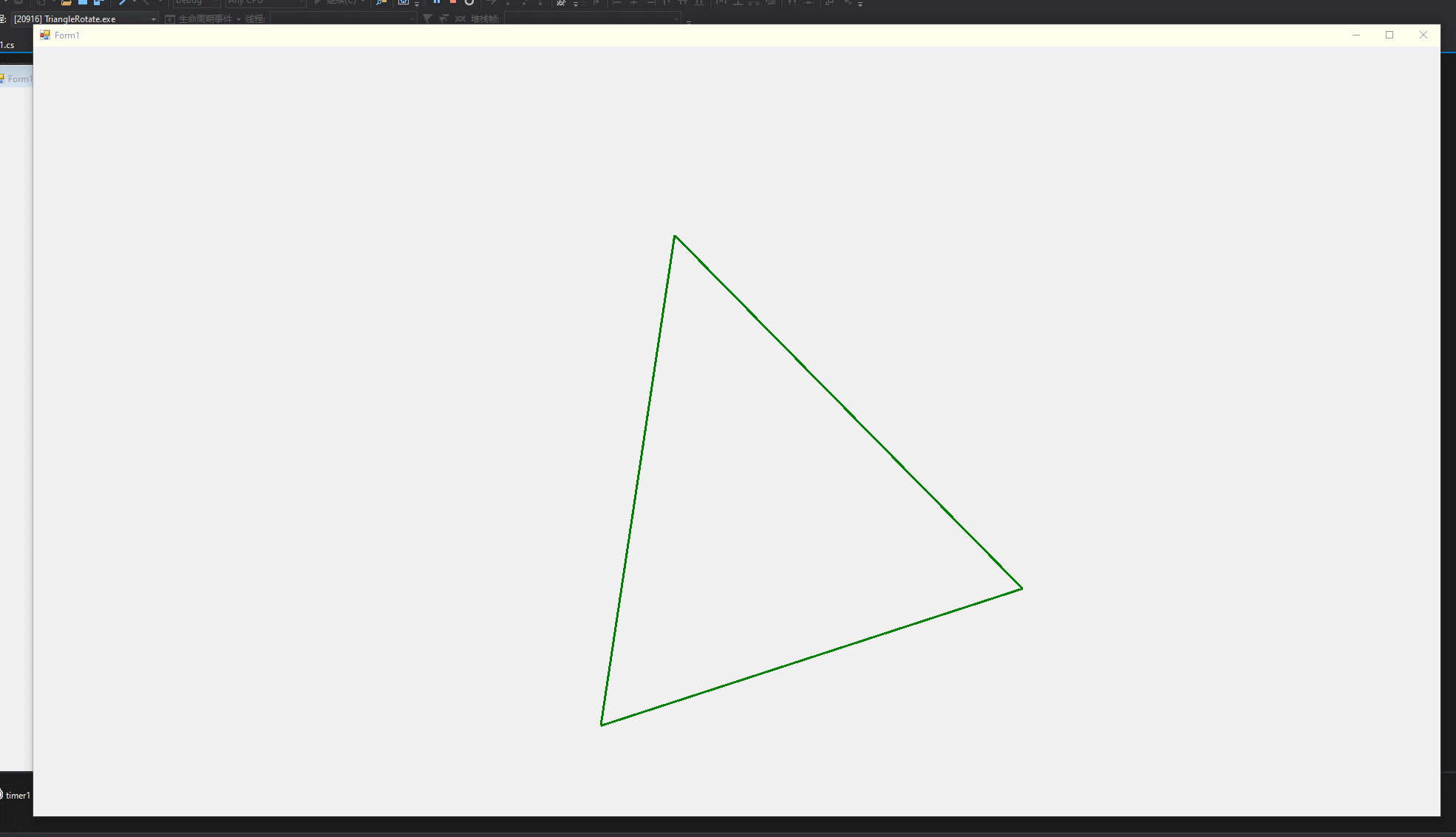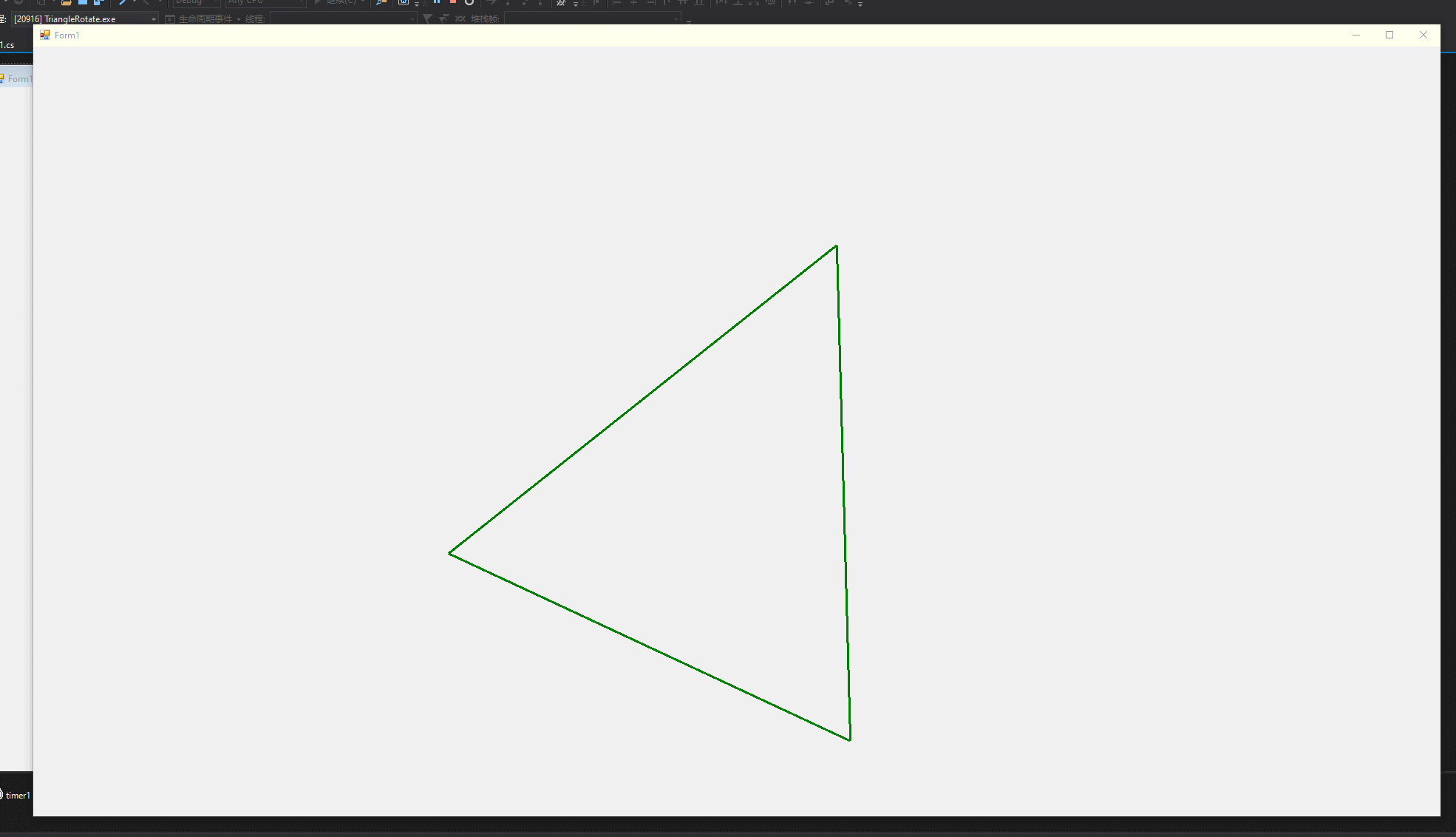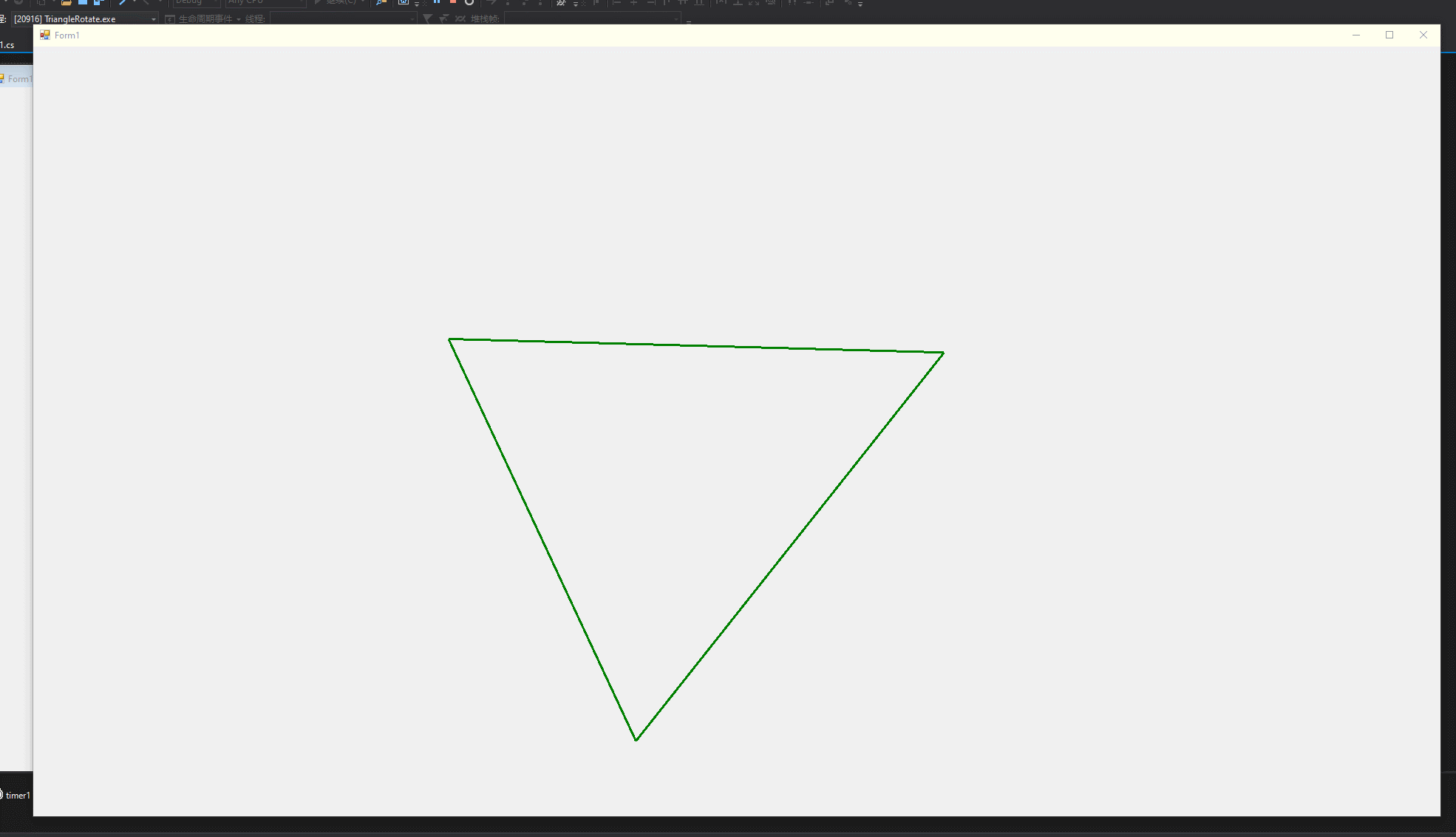




 本文详细介绍了Unity Shader中CG提供的各类标准函数,包括数学、几何、纹理映射、偏导和调试函数,以及如何使用这些函数进行高效计算。此外,通过实例展示了如何使用2D旋转矩阵实现三角形绕中心旋转的视觉效果。
本文详细介绍了Unity Shader中CG提供的各类标准函数,包括数学、几何、纹理映射、偏导和调试函数,以及如何使用这些函数进行高效计算。此外,通过实例展示了如何使用2D旋转矩阵实现三角形绕中心旋转的视觉效果。
















 1481
1481

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








