前言:Unity寻路专题还没有结束,还会有后续文章来讲比A*更高效的算法,当然那些算法的难度也会比较高,当然理解所花费的时间也更多,短期内可能会出一些关于优化的文章,让你知道能从哪些方面去优化算法。
今天先解决一些简单的优化,还是从最简单的BFS和DFS开始,我们已经知道了BFS和DFS的算法流程,然后进一步学习了Dijkstra算法,双向BFS算法,A算法。我们可以发现这三种算法都是从BFS演化来的,首先Dijkstra算法就是BFS在有权图的应用,简单来说就是BFS的寻路过程是没有距离这个概念的,每一步都是它周围的四个点,距离都一样。而Dijkstra则考虑了下一个点与当前点的距离大小。而A自然不用说,进一步优化了Dijkstra。双向BFS更不用说,名字就能看出来和BFS的关系。那你可能会问,这些寻路算法怎么都与BFS有关,和BFS同级的DFS难道就没有一个算法与它有关吗?今天就来介绍一个与DFS有关的算法——IDA*算法。
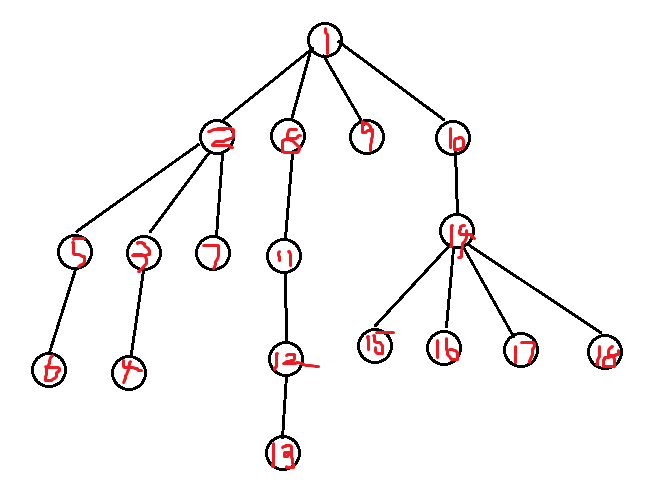
我们可以把地图的节点看做一颗多叉树,如图:DFS的过程就是先沿着左子树一直搜索下去,没有节点了就回溯,然后沿着第二条分支搜索下去.......,这里就有一个问题:要是地图很大导致左子树可以无限延伸下去,而我们要找的节点假设为图中的9,DFS就会一直在左子树搜索,根本找不到9这一节点。为了解决这一问题,我们可以在DFS的搜索过程中给它限制一个深度d,每次搜到第d层就回溯(前提是终点的深度要小于等于d),当然光靠这一约束条件会存在很多重复搜索的点,这时候我们再利用A启发式搜索的特点。我们设计一个估价函数, 估算从每个状态到目标状态需要的步数。然后,以迭代加深DFS的搜索框架为基础,把原来简单的深度限制加强为:若当前深度+未来估计步数深度限制,则立即从当前分支回溯。这就是IDA算法。
基础框架: 在前面的DFS框架上,添加一个if语句判断,看当前节点的深度与maxDepth的关系: ①如果是大于关系,直接跳过当前节点,不做处理。 ②如果是等于关系,就看该点是不是终点,是就找到了路径,不是则同上处理。 ③如果是小于关系,再判断H(n)+当前深度与maxDepth的关系,如果大于就跳过。小于等于都进栈【H(n)为估值函数】


效果图:
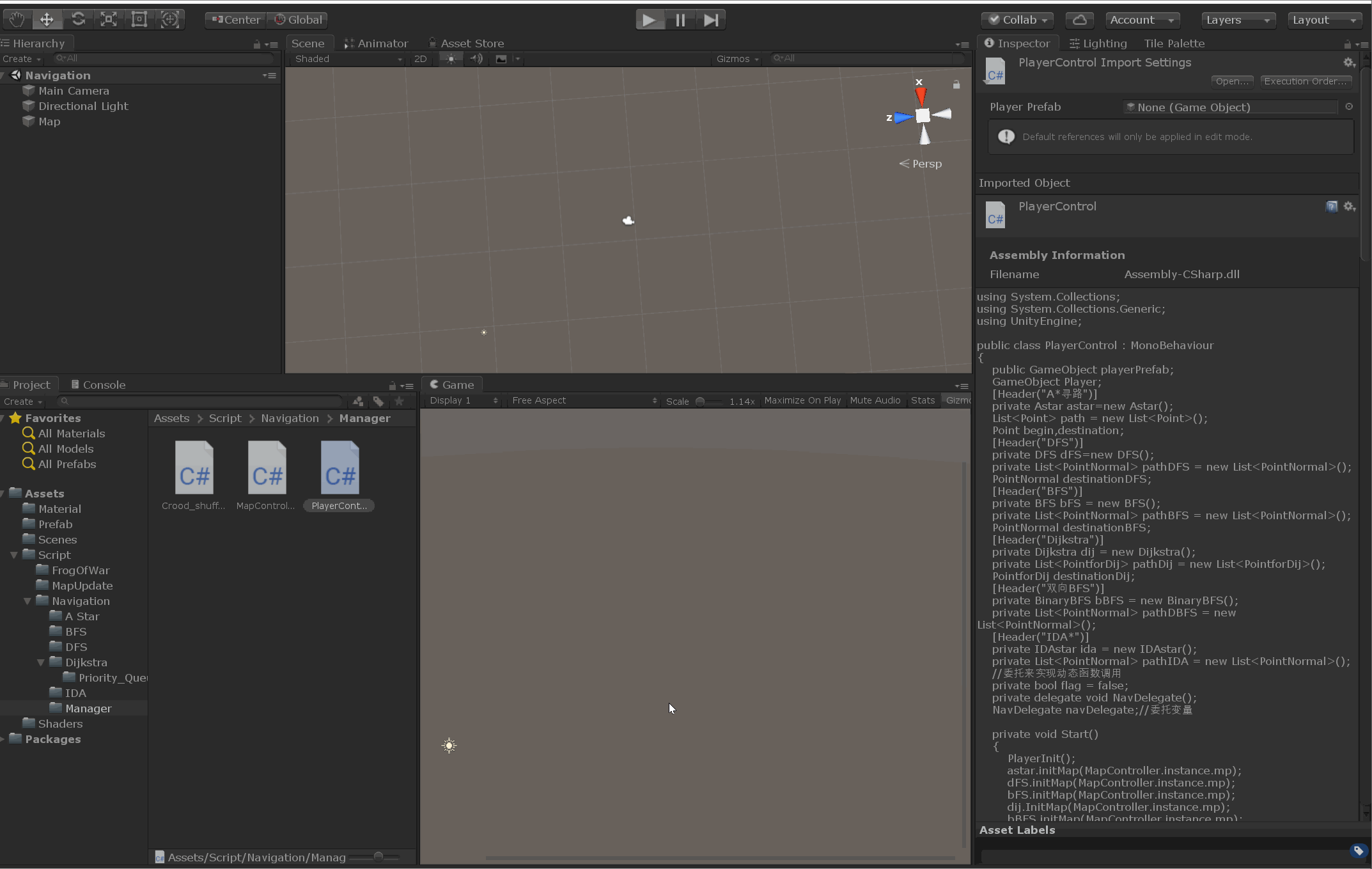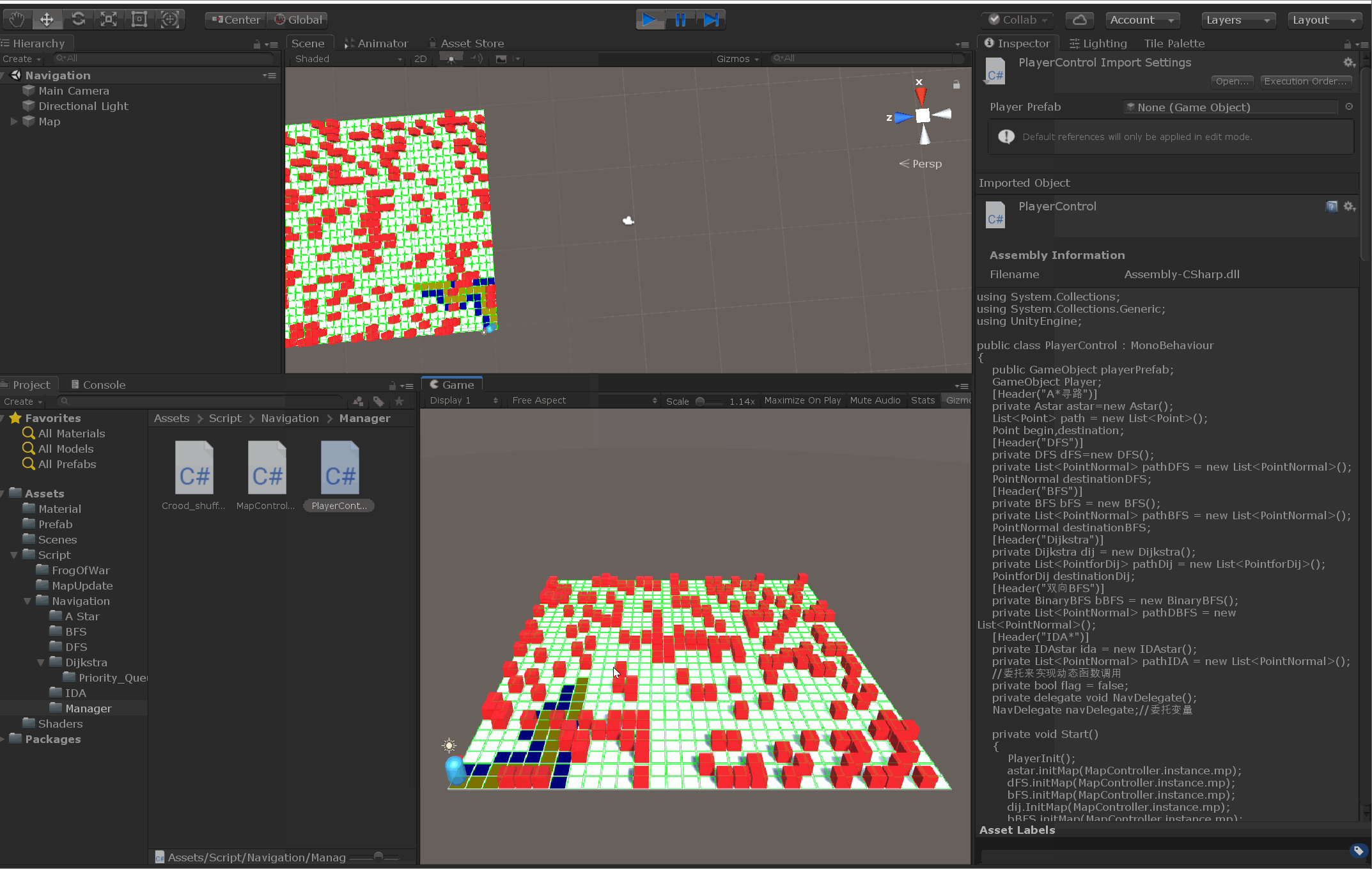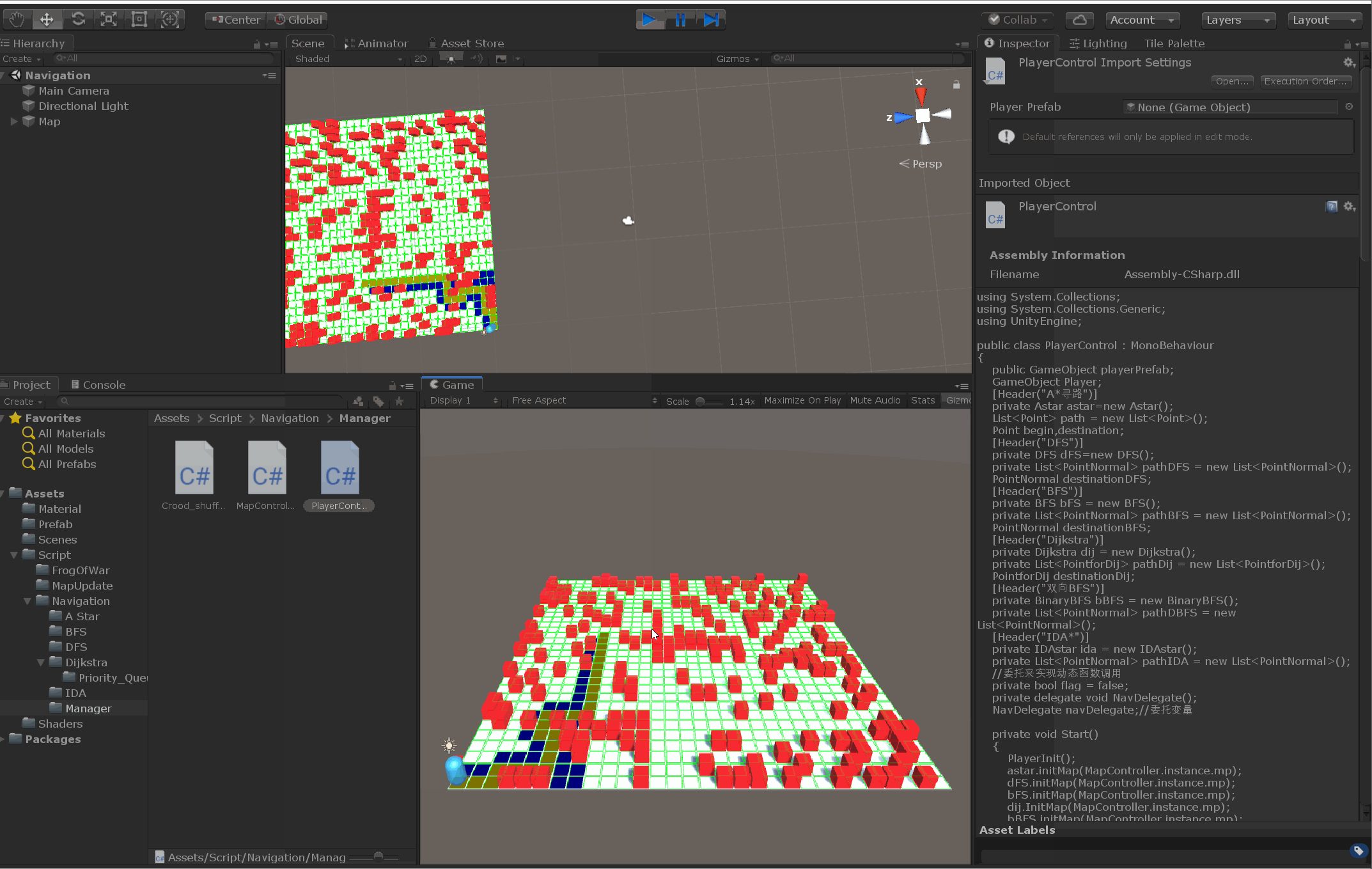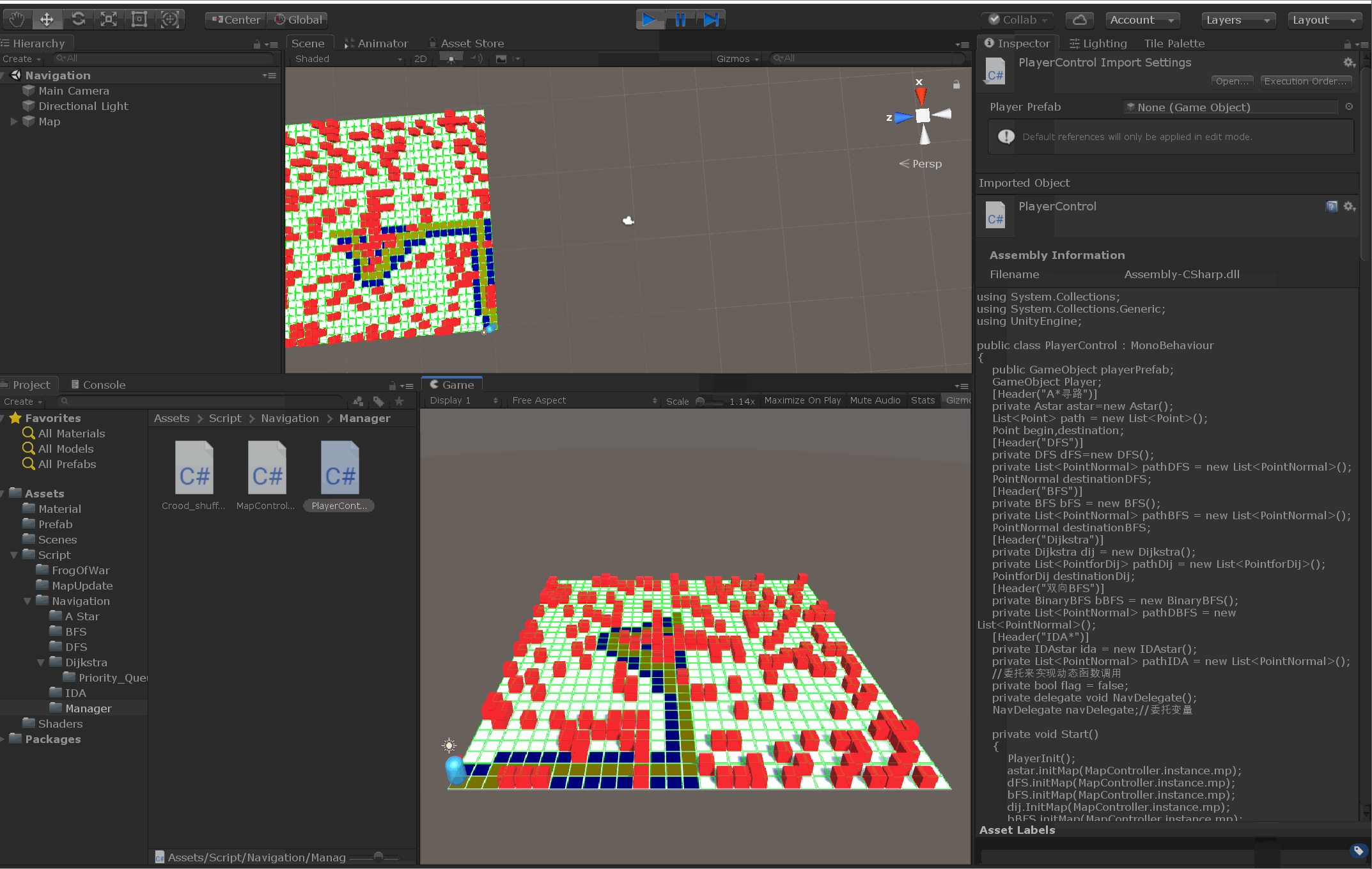




 本文介绍了与DFS相关的IDA*算法,它是为了解决大规模地图中DFS的效率问题。通过限制深度并结合A*启发式搜索,IDA*在有限时间内更高效地寻找路径。通过实例和框架解释,展示了如何在实际寻路问题中应用这一算法。
本文介绍了与DFS相关的IDA*算法,它是为了解决大规模地图中DFS的效率问题。通过限制深度并结合A*启发式搜索,IDA*在有限时间内更高效地寻找路径。通过实例和框架解释,展示了如何在实际寻路问题中应用这一算法。
















 1232
1232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








