基于布鲁姆教学理论的自动控制原理零基础学习指南

引言

自动控制原理是工程学科的核心课程之一，涉及系统建模、分析与设计，广泛应用于机器人、航空航天、工业自动化等领域。然而，对于零基础学习者而言，这门课程往往因抽象性强、数学要求高而显得晦涩难懂。作为自动控制原理课程的学习者及知识实践者，我深知教学方法的的重要性。布鲁姆教学理论（Bloom's Taxonomy）提供了一个系统化的教育框架，通过六个认知层次（记忆、理解、应用、分析、综合、评价）帮助初学者循序渐进地构建知识体系。本文将基于这一理论，分享如何针对零基础展开自动控制原理的串讲与核心知识归纳，旨在帮助初学者克服学习障碍，夯实基础。本文内容基于多年教学实践，结合实例与公式，力求严谨、清晰，适用于优快云读者中的学生和自学者。

---

布鲁姆教学理论概述

布鲁姆教学理论由教育心理学家本杰明·布鲁姆提出，将学习目标分为六个层次，从低阶思维到高阶思维递进：

• 记忆：记住基本事实和概念。

• 理解：解释和归纳知识。

• 应用：在具体情境中使用知识。

• 分析：分解系统并识别关系。

• 综合：整合元素以创建新方案。

• 评价：基于标准判断和批判。

在自动控制原理教学中，这一理论可帮助从死记硬背过渡到创新应用，尤其适合零基础学习者。下面，我将按这六个层次展开课程串讲。

---

按布鲁姆层次展开自动控制原理教学

记忆层：夯实基础概念

对于零基础学生，首要任务是记忆核心术语和基本公式。这一层次强调反复练习与联想记忆，避免过早深入复杂理论。

核心知识：

• 基本定义：系统、输入、输出、反馈、控制器、被控对象。

• 数学基础：微分方程表示动态系统。例如，一阶系统的微分方程为：

  

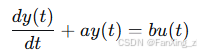
  其中，y(t) 是输出，u(t) 是输入，a 和 b是常数。

• 关键术语：开环控制、闭环控制、稳定性、稳态误差。

方法：通过 flashcards 或思维导图帮助学生记忆。例如，让学生列出控制系统的组成部分，并复述反馈的定义。

理解层：解释原理与关系

在记忆基础上，引导学生理解“为什么”和“如何工作”。重点在于用通俗语言解释抽象概念，并建立知识间的联系。

核心知识：

• 反馈原理：负反馈如何抑制扰动，提高系统精度。用框图表示：

  系统框图： R(s)→控制器→被控对象→Y(s)→反馈回路系统框图： R(s)→控制器→被控对象→Y(s)→反馈回路

• 传递函数：作为系统的频域表示，定义为输出拉普拉斯变换与输入拉普拉斯变换之比：

  

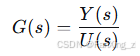
  例如，一阶系统的传递函数为：

• 

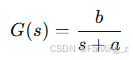
• 稳定性概念：通过极点位置判断——所有极点实部为负时系统稳定。

方法：使用类比法，如将反馈比作 thermostat 控制温度。通过例题解释传递函数的推导过程。

应用层：解决简单问题

学生将所学知识应用于实际场景，培养解决问题的能力。这一层次强调动手实践和模拟。

核心知识：

• 时域分析：计算阶跃响应和稳态误差。例如，给定传递函数 G(s)=1/(s+1)​，求单位阶跃输入的输出响应。

• PID 控制器基础：比例-积分-微分控制器的形式：

  

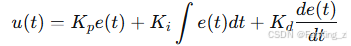
  其中，e(t)e 是误差信号。

• 仿真工具：使用 MATLAB/Simulink 进行系统模拟。

方法：布置简单设计题，如设计一个温度控制系统，要求学生计算 PID 参数并仿真。举例说明：如何调节 KpKp​ 以减少超调。

分析层：分解系统与识别模式

引导学生分析复杂系统，识别组件间的关系和性能指标。这一层次培养逻辑思维。

核心知识：

• 频域分析：Bode 图和 Nyquist 图的绘制与解读。Bode 图显示幅频和相频特性，例如：

  

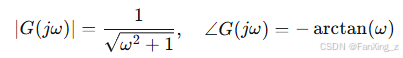
• 稳定性判据：Nyquist 判据和 Routh-Hurwitz 判据的应用。

• 系统性能指标：上升时间、调节时间、超调量。

方法：给定一个二阶系统 ​​，让学生分析 ζ 对稳定性的影响。通过案例研究，如分析飞机姿态控制系统的频域响应。

综合层：设计与创新

学生整合知识，设计新控制系统或优化现有方案。这一层次强调创造性和系统思维。

核心知识：

• 控制器设计：基于性能要求综合 PID 参数或状态反馈控制器。

• 状态空间法：多变量系统的表示：

  

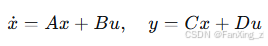
  其中，x 是状态向量。

• 鲁棒控制：考虑不确定性下的设计。

方法：项目式学习，例如设计一个无人机悬停控制系统，要求结合时域和频域方法。学生需提交设计报告，包括数学模型和仿真结果。

评价层：批判与优化

最高层次要求学生评估不同控制策略的优劣，并提出改进建议。这培养批判性思维和工程判断力。

核心知识：

• 性能比较：基于指标如ISE（积分平方误差）评价控制器：

  

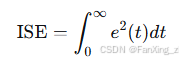
• 现实约束：考虑成本、能耗和实时性。

• 前沿话题：如自适应控制与智能控制的优缺点。

方法：组织辩论或案例分析，例如比较传统 PID 与模糊控制在复杂环境中的效果。让学生撰写评论文，分析某工业控制系统的局限性。

核心知识归纳总结

基于以上教学序列，以下是自动控制原理的核心知识总结，适用于零基础学生复习与自测：

1. 基本概念：

   • 控制系统组成：输入、输出、控制器、反馈。

   • 数学基础：微分方程和拉普拉斯变换。

   • 关键公式：传递函数 G(s)=Y(s)/U(s)。

2. 系统分析：

   • 时域：稳定性（极点分析）、稳态误差。

   • 频域：Bode 图与 Nyquist 图用于稳定性判断。

   • 性能指标：上升时间、超调量等。

3. 控制系统设计：

   • PID 控制器：公式 ​。

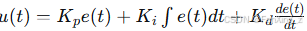   • 设计方法：基于根轨迹或频域响应调参。

   • 高级主题：状态空间法适用于多输入多输出系统。

4. 工具与实践：

   • 仿真软件：MATLAB/Simulink 用于验证设计。

   • 实践原则：从简单系统入手，逐步扩展到复杂应用。

这一归纳强调知识的层次性，学生可参照布鲁姆理论自查学习进度。例如，记忆层需熟记公式，而评价层应能批判性评估设计。

结论

自动控制原理的学习并非一蹴而就，尤其对零基础学生而言，采用布鲁姆教学理论可以系统化地构建知识体系，从记忆到评价逐步深化。作为教授，我建议学生注重基础概念的理解，并通过实践强化应用。本文的串讲与总结旨在提供一个清晰路线图，帮助读者克服初始障碍，迈向自动控制领域的深入探索。未来，可结合数字化工具和项目学习进一步优化教学。如果您是初学者，不妨从记忆层开始，逐步挑战更高层次——控制世界的奥秘，正待您去揭开。

参考文献

• Bloom, B. S. (1956). Taxonomy of Educational Objectives. Handbook I: Cognitive Domain.

• Dorf, R. C., & Bishop, R. H. (2016). Modern Control Systems. Pearson.

• MATLAB Documentation. MathWorks.