注:本文为 “仿射变换” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
什么是仿射变换
彬彬侠 原创于 2025-01-13 21:36:33 发布
一、仿射变换的定义
仿射变换(Affine Transformation)是一类重要的几何变换,由线性变换与平移操作组合而成,其特征是保持图形的平直性与线段比例关系。具体而言,仿射变换会将直线映射为直线,维持不同线段之间的长度比例,但可能改变图形的角度、大小及形状。
该变换在计算机视觉、图像处理、深度学习、GIS 空间坐标转换等多个领域具有广泛应用,例如图像的旋转、缩放、平移、剪切操作,以及不同坐标系之间的空间直角坐标转换等场景,均以仿射变换为技术支撑。
二、仿射变换的形式
(一)通用向量形式
仿射变换的通用数学表达式为:
y
=
A
x
+
b
\mathbf{y} = \mathbf{A}\mathbf{x} + \mathbf{b}
y=Ax+b
其中:
- x \mathbf{x} x:原始坐标(输入向量),通常为 n n n 维向量;
- y \mathbf{y} y:变换后的坐标(输出向量),与输入向量维度一致;
- A \mathbf{A} A:线性变换矩阵,维度为 n × n n \times n n×n,负责实现缩放、旋转、剪切等线性操作;
- b \mathbf{b} b:平移向量,维度为 n n n 维,用于控制坐标的平移偏移。
(二)二维平面具体形式
在二维平面坐标系中,仿射变换的代数表达式可细化为:
x
′
=
a
11
x
+
a
12
y
+
t
x
y
′
=
a
21
x
+
a
22
y
+
t
y
x' = a_{11}x + a_{12}y + t_x\\ y' = a_{21}x + a_{22}y + t_y
x′=a11x+a12y+txy′=a21x+a22y+ty
其中:
- x , y x, y x,y:原始坐标值;
- x ′ , y ′ x', y' x′,y′:变换后的坐标值;
- a 11 , a 12 , a 21 , a 22 a_{11}, a_{12}, a_{21}, a_{22} a11,a12,a21,a22:线性变换参数,分别对应缩放、旋转、剪切等操作的量化指标;
- t x , t y t_x, t_y tx,ty:平移参数,分别表示 x x x 方向、 y y y 方向的平移距离。
三、仿射变换的基本操作
仿射变换通过平移、缩放、旋转、剪切四种基本操作的组合实现复杂变换,每种基本操作均有明确的数学表达与几何意义:
(一)平移(Translation)
平移是仅改变图形位置而不改变形状、大小和方向的操作,其变换公式为:
x
′
=
x
+
t
x
y
′
=
y
+
t
y
x' = x + t_x\\ y' = y + t_y
x′=x+txy′=y+ty
其中
t
x
t_x
tx 为
x
x
x 方向平移量,
t
y
t_y
ty 为
y
y
y 方向平移量。
(二)缩放(Scaling)
缩放用于调整图形的尺寸大小,可分为均匀缩放(
x
,
y
x, y
x,y 方向缩放因子相同)和非均匀缩放(
x
,
y
x, y
x,y 方向缩放因子不同),变换公式为:
x
′
=
s
x
⋅
x
y
′
=
s
y
⋅
y
x' = s_x \cdot x\\ y' = s_y \cdot y
x′=sx⋅xy′=sy⋅y
其中
s
x
s_x
sx 为
x
x
x 方向缩放因子,
s
y
s_y
sy 为
y
y
y 方向缩放因子;当
s
x
=
s
y
>
1
s_x = s_y > 1
sx=sy>1 时图形放大,当
0
<
s
x
=
s
y
<
1
0 < s_x = s_y < 1
0<sx=sy<1 时图形缩小。
(三)旋转(Rotation)
旋转是图形绕某一中心点(默认原点)按指定角度转动的操作,二维平面中绕原点逆时针旋转
θ
\theta
θ 弧度的变换公式为:
x
′
=
x
⋅
cos
θ
−
y
⋅
sin
θ
y
′
=
x
⋅
sin
θ
+
y
⋅
cos
θ
x' = x \cdot \cos\theta - y \cdot \sin\theta\\ y' = x \cdot \sin\theta + y \cdot \cos\theta
x′=x⋅cosθ−y⋅sinθy′=x⋅sinθ+y⋅cosθ
若需绕任意点
(
x
0
,
y
0
)
(x_0, y_0)
(x0,y0) 旋转,需先将图形平移至原点,旋转后再平移回原中心点位置。
(四)剪切(Shear)
剪切是使图形产生“错切”变形的操作,会将矩形等规则图形转化为平行四边形,分为水平剪切与垂直剪切,变换公式分别为:
- 水平剪切: x ′ = x + k x ⋅ y x' = x + k_x \cdot y x′=x+kx⋅y, y ′ = y y' = y y′=y( k x k_x kx 为水平剪切因子);
- 垂直剪切: x ′ = x x' = x x′=x, y ′ = y + k y ⋅ x y' = y + k_y \cdot x y′=y+ky⋅x( k y k_y ky 为垂直剪切因子)。
四、仿射变换的矩阵形式(齐次坐标)
为了将线性变换与平移操作统一为矩阵乘法形式,方便计算与组合,仿射变换通常采用齐次坐标表示。将
n
n
n 维坐标扩展为
n
+
1
n+1
n+1 维,二维仿射变换的齐次矩阵形式为:
[
x
′
y
′
1
]
=
[
a
11
a
12
t
x
a
21
a
22
t
y
0
0
1
]
[
x
y
1
]
\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix}= \begin{bmatrix} a_{11} & a_{12} & t_x \\ a_{21} & a_{22} & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
x′y′1
=
a11a210a12a220txty1
xy1
其中,3×3 矩阵的前 2×2 子矩阵 (\begin{bmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \end{bmatrix}) 对应线性变换(缩放、旋转、剪切),最后一列的前两个元素 ((t_x, t_y)) 对应平移操作,最后一行固定为 ((0, 0, 1)) 以保证齐次坐标的特性。
通过齐次矩阵形式,多次仿射变换可通过矩阵乘法实现组合,无需单独处理线性变换与平移操作,大幅简化了复杂变换的计算流程。
五、仿射变换的关键性质
- 保持平直性:变换后直线仍为直线,不会出现曲线化变形,且平行线经过变换后依然保持平行;
- 保持比例性:同一直线上的线段长度比例,在变换后保持不变;
- 共线性与共面性不变:共线的点经过变换后仍共线,共面的点经过变换后仍共面;
- 角度与面积可变性:除平移、均匀缩放、旋转等刚体变换外,剪切、非均匀缩放等操作会改变图形的角度与面积。
六、仿射变换的典型应用场景
(一)图像处理领域
- 基础操作:图像的旋转、缩放、平移、剪切,用于图像裁剪、尺寸标准化等;
- 数据增强:深度学习训练中,通过随机仿射变换生成多样化样本,提升模型泛化能力;
- 图像配准:多幅同源图像的对齐的操作,消除拍摄角度、位置差异。
(二)计算机视觉领域
- 目标检测:候选窗口的变换与调整,适配不同尺度、角度的目标;
- 姿态估计:通过仿射变换还原物体的空间姿态;
- 图像校正:修正拍摄过程中产生的透视畸变、倾斜畸变。
(三)GIS 与空间数据处理
- 空间直角坐标转换:不同坐标系(如屏幕坐标与地理坐标)之间的转换,是 GIS 二次开发的关键技术之一;
- 地图投影变换:部分地图投影的计算过程依赖仿射变换的线性变换特性。
(四)游戏与计算机图形学
- 模型变换:游戏角色、场景物体的平移、旋转、缩放,实现动态展示效果;
- 场景渲染:通过仿射变换调整视角与物体位置,构建三维场景的二维投影。
七、PyTorch 中的仿射变换实现
PyTorch 提供了 torch.nn.functional.affine_grid 和 torch.nn.functional.grid_sample 两个关键函数,用于高效实现图像的仿射变换,适用于深度学习中的数据处理与模型训练场景。
示例:图像的旋转与平移组合变换
import torch
import torch.nn.functional as F
# 1. 定义仿射变换矩阵(绕原点逆时针旋转 30° + 无平移)
theta = torch.tensor([
[torch.cos(torch.tensor(30 * torch.pi / 180)), -torch.sin(torch.tensor(30 * torch.pi / 180)), 0.0],
[torch.sin(torch.tensor(30 * torch.pi / 180)), torch.cos(torch.tensor(30 * torch.pi / 180)), 0.0]
], dtype=torch.float32).unsqueeze(0) # 添加 batch 维度,形状为 (1, 2, 3)
# 2. 创建仿射变换网格(输出图像尺寸为 (1, 1, 256, 256),即 batch=1、channel=1、高=256、宽=256)
grid = F.affine_grid(theta, size=(1, 1, 256, 256), align_corners=False)
# 3. 生成输入图像(随机生成 1 张 1 通道、256×256 尺寸的图像)
input_image = torch.rand(1, 1, 256, 256, dtype=torch.float32)
# 4. 应用仿射变换
output_image = F.grid_sample(input_image, grid, align_corners=False)
# 输出结果信息
print("输入图像形状:", input_image.shape)
print("输出图像形状:", output_image.shape)
代码说明
affine_grid:根据变换矩阵theta和目标输出尺寸生成变换网格,网格定义了输入图像每个像素在输出图像中的对应位置;grid_sample:根据生成的网格,对输入图像进行采样,实现仿射变换;align_corners:控制网格采样时是否对齐图像角落像素,False 为默认推荐设置,避免边缘像素畸变。
八、总结
仿射变换是一类兼具灵活性与实用性的几何变换,通过线性变换与平移的组合,能够实现图形的平移、缩放、旋转、剪切等多种操作。其优势在于保持平直性与线段比例关系,同时通过齐次坐标形式实现复杂变换的统一计算。
从理论层面,仿射变换的数学原理清晰,矩阵表达与参数求解逻辑严谨;从应用层面,其广泛覆盖图像处理、计算机视觉、GIS、深度学习等多个领域,是技术落地的关键工具。深入理解仿射变换的原理与性质,能够为相关领域的算法设计、数据处理提供坚实的理论支撑,助力优化技术方案与提升应用效果。
图像几何变换之仿射变换原理及实现
Eating Lee 原创于 2019-03-19 23:03:00 发布
一、仿射变换的数学基础与定义
1.1 定义
仿射变换是平面内点集到另一平面点集的映射关系,其特征是保持图形的“平直性”——即直线经过变换后仍为直线,且平行线变换后依然平行。该变换在图像处理领域应用广泛,包括但不限于图像配准、几何畸变纠正、纹理映射及全景图像拼接等场景。
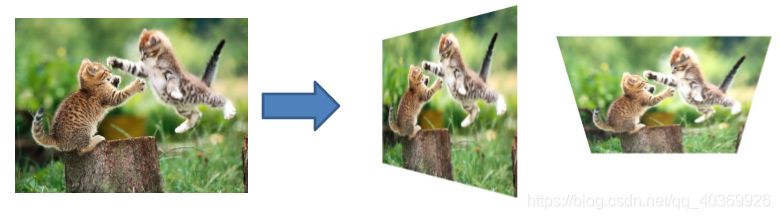
1.2 数学表示
(1)坐标变换表达式
仿射变换可描述为二维直角坐标
(
x
,
y
)
(x, y)
(x,y) 到目标坐标
(
u
,
v
)
(u, v)
(u,v) 的线性变换与平移变换的组合,其代数形式为:
{
u
=
a
11
x
+
a
12
y
+
t
x
v
=
a
21
x
+
a
22
y
+
t
y
\begin{cases} u = a_{11}x + a_{12}y + t_x \\ v = a_{21}x + a_{22}y + t_y \end{cases}
{u=a11x+a12y+txv=a21x+a22y+ty
其中,
a
11
,
a
12
,
a
21
,
a
22
a_{11}, a_{12}, a_{21}, a_{22}
a11,a12,a21,a22 构成线性变换系数,
t
x
,
t
y
t_x, t_y
tx,ty 为平移分量。
(2)齐次坐标矩阵表示
为统一线性变换与平移变换的矩阵运算形式,引入齐次坐标(将二维点 ( x , y ) (x, y) (x,y) 扩展为三维向量 ( x , y , 1 ) (x, y, 1) (x,y,1)),此时仿射变换可表示为矩阵乘法形式:
[ u v 1 ] ⏟ 输出:目标齐次坐标 X ′ = [ [ a 11 a 21 0 ] ⏟ x 轴基向量变换结果 [ a 12 a 22 0 ] ⏟ y 轴基向量变换结果 [ t x t y 1 ] ⏟ 原点平移向量 ] ⏟ 仿射变换矩阵 H 行 1:x 坐标映射方程 行 2:y 坐标映射方程 行 3:齐次坐标约束 ⋅ [ x y 1 ] ⏟ 输入:原始齐次坐标 X \underbrace{\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}}_{\text{输出:目标齐次坐标 } \mathbf{X}'}= \underbrace{ \left[ \underbrace{\begin{bmatrix} a_{11} \\ a_{21} \\ 0 \end{bmatrix}}_{\text{x 轴基向量变换结果}}\ \underbrace{\begin{bmatrix} a_{12} \\ a_{22} \\ 0 \end{bmatrix}}_{\text{y 轴基向量变换结果}}\ \underbrace{\begin{bmatrix} t_x \\ t_y \\ 1 \end{bmatrix}}_{\text{原点平移向量}} \right] }_{\begin{array}{c}\text{仿射变换矩阵 } \mathbf{H} \\ \hline \text{行 1:x 坐标映射方程} \\ \text{行 2:y 坐标映射方程} \\ \text{行 3:齐次坐标约束}\end{array}} \cdot \underbrace{\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}}_{\text{输入:原始齐次坐标 } \mathbf{X}} 输出:目标齐次坐标 X′ uv1 =仿射变换矩阵 H行 1:x 坐标映射方程行 2:y 坐标映射方程行 3:齐次坐标约束 x 轴基向量变换结果 a11a210 y 轴基向量变换结果 a12a220 原点平移向量 txty1 ⋅输入:原始齐次坐标 X xy1
对比一般投影变换矩阵 H 投影 = [ h 00 h 01 h 02 h 10 h 11 h 12 h 20 h 21 h 22 ] \mathbf{H}_{\text{投影}} = \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & h_{22} \end{bmatrix} H投影= h00h10h20h01h11h21h02h12h22 ,仿射变换的约束条件为 h 20 = 0 h_{20} = 0 h20=0、 h 21 = 0 h_{21} = 0 h21=0、 h 22 = 1 h_{22} = 1 h22=1,因此仅含 6 个独立未知参数( a 11 , a 12 , a 21 , a 22 , t x , t y a_{11}, a_{12}, a_{21}, a_{22}, t_x, t_y a11,a12,a21,a22,tx,ty)。
(3)非齐次坐标还原
若已知齐次坐标变换结果
(
w
u
,
w
v
,
w
)
(w u, w v, w)
(wu,wv,w)(
w
≠
0
w \neq 0
w=0),可通过以下公式还原二维直角坐标:
u
=
a
11
x
+
a
12
y
+
t
x
1
v
=
a
21
x
+
a
22
y
+
t
y
1
u = \frac{a_{11}x + a_{12}y + t_x}{1}\\[1em] v = \frac{a_{21}x + a_{22}y + t_y}{1}
u=1a11x+a12y+txv=1a21x+a22y+ty
因仿射变换中分母恒为 1,无需额外归一化操作。
二、仿射变换的几何分解
仿射变换可分解为平移、旋转、尺度变换等基本几何变换的复合运算,各基本变换的矩阵形式与几何意义如下:
2.1 平移变换
(1)几何意义
将平面内所有点沿 x x x 轴、 y y y 轴方向分别移动 t x t_x tx、 t y t_y ty 个单位,图形形状与大小保持不变。
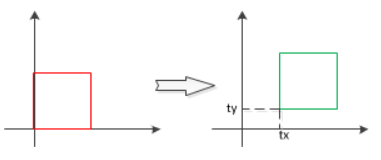
(2)数学形式
- 代数表达式:
{ u = x + t x v = y + t y \begin{cases} u = x + t_x \\ v = y + t_y \end{cases} {u=x+txv=y+ty - 齐次坐标矩阵:
H 平移 = [ 1 0 t x 0 1 t y 0 0 1 ] \mathbf{H}_{\text{平移}} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} H平移= 100010txty1
其中 t x , t y t_x, t_y tx,ty 为平移参数,决定移动方向与距离。
2.2 旋转变换
(1)几何意义
将平面内所有点绕原点(或指定旋转中心)旋转 θ \theta θ 角,旋转方向遵循右手定则( θ > 0 \theta > 0 θ>0 时逆时针旋转),图形形状与大小保持不变。
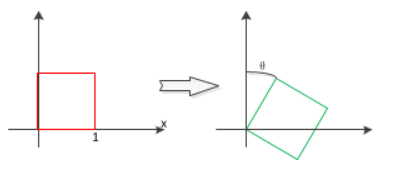
(2)数学形式
- 代数表达式(绕原点旋转):
{ u = x cos θ − y sin θ v = x sin θ + y cos θ \begin{cases} u = x \cos\theta - y \sin\theta \\ v = x \sin\theta + y \cos\theta \end{cases} {u=xcosθ−ysinθv=xsinθ+ycosθ - 齐次坐标矩阵:
H 旋转 = [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] \mathbf{H}_{\text{旋转}} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} H旋转= cosθsinθ0−sinθcosθ0001
若需绕任意点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0) 旋转,需先将图形平移至原点(减去 ( x 0 , y 0 ) (x_0, y_0) (x0,y0)),旋转后再平移回原位置(加上 ( x 0 , y 0 ) (x_0, y_0) (x0,y0)),即复合变换 H = H 平移 ( x 0 , y 0 ) ⋅ H 旋转 ⋅ H 平移 ( − x 0 , − y 0 ) \mathbf{H} = \mathbf{H}_{\text{平移}(x_0,y_0)} \cdot \mathbf{H}_{\text{旋转}} \cdot \mathbf{H}_{\text{平移}(-x_0,-y_0)} H=H平移(x0,y0)⋅H旋转⋅H平移(−x0,−y0)。
2.3 尺度变换
(1)几何意义
将平面内所有点沿 x x x 轴、 y y y 轴方向分别按比例 s x s_x sx、 s y s_y sy 缩放,改变图形大小但不改变形状(当 s x = s y s_x = s_y sx=sy 时为均匀缩放, s x ≠ s y s_x \neq s_y sx=sy 时为非均匀缩放)。
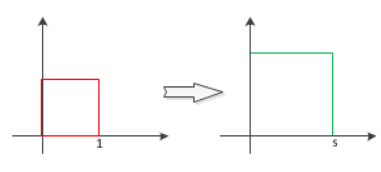
(2)数学形式
- 代数表达式:
{ u = s x ⋅ x v = s y ⋅ y \begin{cases} u = s_x \cdot x \\ v = s_y \cdot y \end{cases} {u=sx⋅xv=sy⋅y - 齐次坐标矩阵:
H 尺度 = [ s x 0 0 0 s y 0 0 0 1 ] \mathbf{H}_{\text{尺度}} = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} H尺度= sx000sy0001
其中 s x > 0 s_x > 0 sx>0、 s y > 0 s_y > 0 sy>0,当 s x = s y = 1 s_x = s_y = 1 sx=sy=1 时为恒等变换(无缩放)。
2.4 刚体变换(旋转+平移+均匀缩放)
(1)几何意义
保持图形形状与内部角度不变的变换,仅改变位置与整体大小,对应物理中的刚体运动(无形变)。
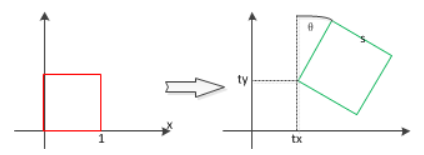
(2)数学形式
- 齐次坐标矩阵:
H 刚体 = [ s cos θ − s sin θ t x s sin θ s cos θ t y 0 0 1 ] \mathbf{H}_{\text{刚体}} = \begin{bmatrix} s \cos\theta & -s \sin\theta & t_x \\ s \sin\theta & s \cos\theta & t_y \\ 0 & 0 & 1 \end{bmatrix} H刚体= scosθssinθ0−ssinθscosθ0txty1
其中:- s s s 为均匀缩放系数( s > 0 s > 0 s>0);
- θ \theta θ 为旋转角度;
- t x , t y t_x, t_y tx,ty 为平移参数。
- 矩阵分解关系: H 刚体 = H 平移 ⋅ H 旋转 ⋅ H 尺度(均匀) \mathbf{H}_{\text{刚体}} = \mathbf{H}_{\text{平移}} \cdot \mathbf{H}_{\text{旋转}} \cdot \mathbf{H}_{\text{尺度(均匀)}} H刚体=H平移⋅H旋转⋅H尺度(均匀),体现变换的复合特性。
三、alpha 通道与图像融合
3.1 定义与作用
alpha 通道是图像中用于表示像素透明度的附加通道,在 32 位 RGB 图像中,每个像素由 R(红)、G(绿)、B(蓝)三个颜色分量与一个 alpha 分量组成(各分量取值范围为 0~255):
- alpha = 0:像素完全透明,融合时不显示该像素;
- alpha = 255:像素完全不透明,融合时完全覆盖目标图像对应位置;
- 0 < alpha < 255:像素半透明,融合时与目标图像按透明度比例混合。
3.2 融合原理
在仿射变换实现图像拼接时,alpha 通道用于控制源图像的显示区域:仅 alpha > 0 的像素会被绘制到目标图像,alpha = 0 的像素则保持目标图像原有内容,从而实现无锯齿的平滑融合效果。
四、仿射变换矩阵的求解
4.1 求解原理
仿射变换矩阵 H \mathbf{H} H 含 6 个独立参数,根据线性方程组求解规则,需至少 3 组不共线的对应点对 ( x i , y i ) ↔ ( u i , v i ) (x_i, y_i) \leftrightarrow (u_i, v_i) (xi,yi)↔(ui,vi)( i = 1 , 2 , 3 i = 1,2,3 i=1,2,3),每组点对可建立 2 个线性方程,共 6 个方程,足以唯一确定所有参数。
若存在多余点对(如 4 组及以上),可通过最小二乘法求解最优矩阵,降低噪声干扰。
4.2 求解步骤
- 数据准备:获取源图像点集 f p = [ x 1 x 2 x 3 y 1 y 2 y 3 1 1 1 ] \mathbf{fp} = \begin{bmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 & 1 \end{bmatrix} fp= x1y11x2y21x3y31 与目标图像对应点集 t p = [ u 1 u 2 u 3 v 1 v 2 v 3 1 1 1 ] \mathbf{tp} = \begin{bmatrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ 1 & 1 & 1 \end{bmatrix} tp= u1v11u2v21u3v31 ,确保点集大小一致且点不共线。
- 坐标归一化:对 f p \mathbf{fp} fp 和 t p \mathbf{tp} tp 进行平移与缩放归一化,使点集均值为 0、标准差为 1,提升数值计算稳定性。
- 矩阵求解:通过奇异值分解(SVD)求解线性方程组 t p = H ⋅ f p \mathbf{tp} = \mathbf{H} \cdot \mathbf{fp} tp=H⋅fp,剔除异常点对影响,得到归一化后的变换矩阵。
- 反归一化:将归一化后的矩阵还原为原始坐标下的仿射变换矩阵 H \mathbf{H} H。
五、仿射变换的代码实现
5.1 开发环境与依赖库
- 编程语言:Python 3.x
- 依赖库:NumPy(数值计算)、PIL(图像读取)、SciPy(矩阵分解与图像变换)、Matplotlib(结果可视化)
5.2 代码实现
(1)主函数(图像读取、参数设置与结果展示)
# -*- coding: utf-8 -*-
import numpy as np
from PIL import Image
from pylab import plt
from scipy import ndimage
from geometry import homography # 自定义矩阵求解模块
# 读取源图像(im1)与目标图像(im2),转换为灰度图
im1 = np.array(Image.open('D:/test/beatles.jpg').convert('L'))
im2 = np.array(Image.open('D:/test/billboard_for_rent.jpg').convert('L'))
# 定义目标区域点集(齐次坐标):按左上角→右上角→右下角→左下角顺序排列
tp = np.array([[120, 260, 260, 120], # 目标点 x 坐标
[16, 16, 305, 305], # 目标点 y 坐标
[1, 1, 1, 1]]) # 齐次坐标分量
# 调用仿射变换函数,将 im1 融合到 im2 的指定区域
im3 = image_in_image(im1, im2, tp)
# 可视化结果
plt.figure(figsize=(12, 4))
plt.gray() # 灰度模式显示
plt.subplot(131)
plt.axis('off')
plt.title('源图像', fontsize=12)
plt.imshow(im1)
plt.subplot(132)
plt.axis('off')
plt.title('目标图像', fontsize=12)
plt.imshow(im2)
plt.subplot(133)
plt.axis('off')
plt.title('仿射变换融合结果', fontsize=12)
plt.imshow(im3)
plt.tight_layout()
plt.show()
(2)图像融合函数 image_in_image(im1, im2, tp)
def image_in_image(im1, im2, tp):
"""
功能:通过仿射变换将源图像 im1 融合到目标图像 im2 的指定区域 tp
参数:
im1: 源图像(numpy 数组)
im2: 目标图像(numpy 数组)
tp: 目标区域点集(3×N 齐次坐标矩阵,N≥3)
返回:
im_fused: 融合后的图像(numpy 数组)
"""
# 获取源图像的高度 m 和宽度 n
m, n = im1.shape[:2]
# 定义源图像的角点集(齐次坐标):左上角→右上角→右下角→左下角
fp = np.array([[0, 0, n, n], # 源点 x 坐标
[0, m, m, 0], # 源点 y 坐标
[1, 1, 1, 1]]) # 齐次坐标分量
# 求解仿射变换矩阵 H
H = homography.Haffine_from_points(tp, fp)
# 应用仿射变换到源图像 im1:使用双线性插值保持图像平滑
im1_warped = ndimage.affine_transform(
im1, H[:2, :2], # 线性变换矩阵
offset=(H[0, 2], H[1, 2]), # 平移分量
output_shape=im2.shape[:2], # 输出图像尺寸(与目标图像一致)
order=1 # 插值方式:1 表示双线性插值
)
# 构建 alpha 通道:变换后非零区域为不透明(1),零区域为透明(0)
alpha = (im1_warped > 0).astype(np.float32)
# 图像融合:(1 - alpha)*im2 + alpha*im1_warped,实现平滑过渡
im_fused = (1 - alpha) * im2 + alpha * im1_warped
return im_fused.astype(np.uint8) # 转换为 8 位图像格式
(3)仿射矩阵求解函数 homography.Haffine_from_points(tp, fp)
def Haffine_from_points(fp, tp):
"""
功能:根据源点集 fp 和目标点集 tp,求解最优仿射变换矩阵 H
参数:
fp: 源点集(3×N 齐次坐标矩阵,N≥3)
tp: 目标点集(3×N 齐次坐标矩阵,N≥3)
返回:
H: 仿射变换矩阵(3×3)
异常:
若 fp 与 tp 尺寸不一致,抛出 RuntimeError
"""
if fp.shape != tp.shape:
raise RuntimeError("源点集与目标点集的尺寸必须一致")
# 步骤 1:对源点集 fp 进行归一化
# 计算 x、y 坐标的均值
mean_fp = np.mean(fp[:2], axis=1) # shape: (2,)
# 计算 x、y 坐标的标准差,避免除以零
std_fp = np.max(np.std(fp[:2], axis=1)) + 1e-9
# 构建归一化矩阵 C1:平移(减去均值)+ 缩放(除以标准差)
C1 = np.diag([1 / std_fp, 1 / std_fp, 1])
C1[0, 2] = -mean_fp[0] / std_fp
C1[1, 2] = -mean_fp[1] / std_fp
# 应用归一化到 fp
fp_normalized = np.dot(C1, fp)
# 步骤 2:对目标点集 tp 进行相同的归一化(保持缩放系数一致)
mean_tp = np.mean(tp[:2], axis=1) # shape: (2,)
C2 = np.diag([1 / std_fp, 1 / std_fp, 1])
C2[0, 2] = -mean_tp[0] / std_fp
C2[1, 2] = -mean_tp[1] / std_fp
# 应用归一化到 tp
tp_normalized = np.dot(C2, tp)
# 步骤 3:构造线性方程组矩阵 A,通过 SVD 求解最优解
# A 的构造:每列对应一组点对的约束,shape: (2N, 6)
A = np.vstack([
np.hstack([fp_normalized[0], fp_normalized[1], np.ones(fp_normalized.shape[1]),
np.zeros(fp_normalized.shape[1]), np.zeros(fp_normalized.shape[1]), np.zeros(fp_normalized.shape[1])]),
np.hstack([np.zeros(fp_normalized.shape[1]), np.zeros(fp_normalized.shape[1]), np.zeros(fp_normalized.shape[1]),
fp_normalized[0], fp_normalized[1], np.ones(fp_normalized.shape[1])])
])
# 构造右侧向量 b,shape: (2N,)
b = tp_normalized[:2].reshape(-1)
# 步骤 4:奇异值分解(SVD)求解最小二乘解
U, S, Vt = np.linalg.svd(A)
# 最小二乘解对应 Vt 的最后一行(奇异值最小的方向)
x = Vt[-1]
# 步骤 5:重构归一化后的仿射矩阵 H_normalized
H_normalized = np.array([
[x[0], x[1], x[2]],
[x[3], x[4], x[5]],
[0, 0, 1]
])
# 步骤 6:反归一化,得到原始坐标下的变换矩阵 H
H = np.dot(np.linalg.inv(C2), np.dot(H_normalized, C1))
# 归一化矩阵:使 H[2,2] = 1(齐次坐标约束)
return H / H[2, 2]
六、实验效果展示
6.1 输入图像
- 源图像(im1):Beatles 人物图像(左侧);
- 目标图像(im2):广告牌背景图像(中间)。
6.2 融合结果


6.3 结果分析
融合后的图像(右侧)中,源图像贴合目标图像的广告牌区域,保持了源图像的比例与角度,且通过 alpha 通道实现了无明显边缘的平滑过渡,验证了仿射变换的几何正确性与实现有效性。
代码实现体现了“数学建模→算法设计→工程实现”逻辑通过对应点集求解仿射矩阵、结合 alpha 通道实现图像融合的流程,实际应用中可通过增加对应点对数量、优化插值算法等方式进一步提升变换精度与图像质量。
七、总结
仿射变换作为一种保持平直性的几何变换,其数学本质是线性变换与平移变换的复合,通过齐次坐标矩阵可实现统一表示与运算。其价值在于能够灵活分解为平移、旋转、尺度等基本变换,满足图像处理中几何校正、图像融合等实际需求。
- 仿射变换 | 原理、矩阵构造(篇 2)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/155754868 - 仿射变换 | 原理、矩阵构造(篇 3)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/155774996
via:
- 什么是仿射变换-优快云博客
https://blog.youkuaiyun.com/u013172930/article/details/145124301 - 图像几何变换之仿射变换原理及实现-优快云博客
https://blog.youkuaiyun.com/qq_40369926/article/details/88672855





















 2811
2811

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








