姿态控制与工程实现 | 旋转矩阵推导、IMU 姿态解算（篇 2）

注：本文为 “姿态控制” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

---

IMU 原理及姿态融合算法详解

原创于 2019-07-28 16:59:26 发布

一、组成

IMU 全称为惯性测量单元（Inertial Measurement Unit），元件包括陀螺仪、加速度计和磁力计。其中，陀螺仪用于测量各轴的角速度，加速度计可获取 $x$、$y$、$z$ 三个方向的线加速度，磁力计能够采集周围环境的磁场信息。其工作是融合三个传感器的输出数据，从而得到高精度的载体姿态信息。

二、原理

a）陀螺仪

陀螺仪基于科里奥利力（Coriolis force）原理检测角速度，该物理概念在大学物理课程中已有涉及，具体原理示意图如下：

当物体以恒定线速度 $v$ 运动时，若受到角速度 $\omega$ 的作用，会在 $v\times \omega$ 的叉乘方向产生科里奥利力。通过测量该力的大小，即可间接获得角速度 $\omega$ 的数值。

在实际的 MEMS（Micro-Electro-Mechanical Systems）传感器中，其结构大致如下：内部敏感单元沿某一方向做往复运动，当存在旋转角速度时，垂直于运动方向会产生科里奥利力。通过检测电容变化反映该力的大小，进而解算出旋转角速度的数值。

b）加速度计

加速度计的工作原理基于牛顿第二定律（$F=ma$），用于测量三轴方向的线加速度。其内部结构包含一个质量块，当受到加速度作用时，质量块会产生位移，两侧的电容传感器可检测该位移量，进而通过换算得到加速度的大小。

c）磁力计

磁力计通过霍尔效应（Hall effect）测量磁场强度，其工作机制为：在导体一端施加电流，当存在外部磁场时，电子会在洛伦兹力作用下向垂直于电流和磁场的方向偏转，导致导体侧面产生电势差。通过测量该电势差的大小及极性，可间接推算出磁场强度的数值。

三、旋转的表达

a）欧拉角

欧拉角是最直观的姿态描述方法，通过绕三个正交轴的依次旋转角度来表征物体姿态，具体示意如下：

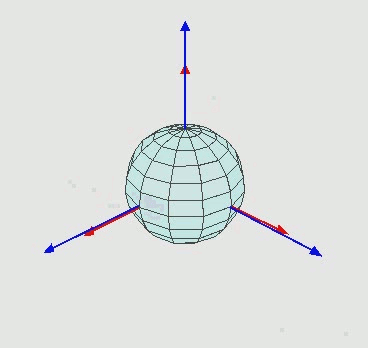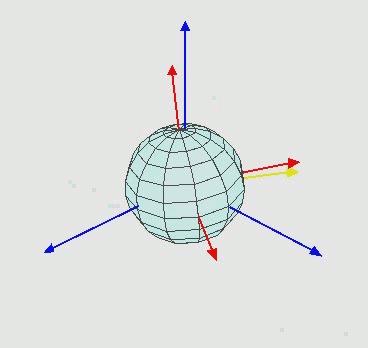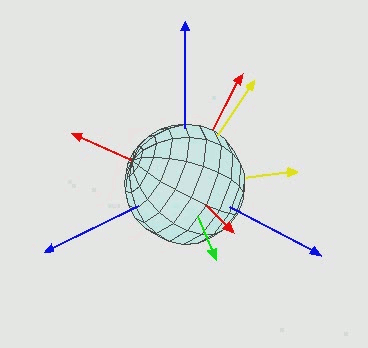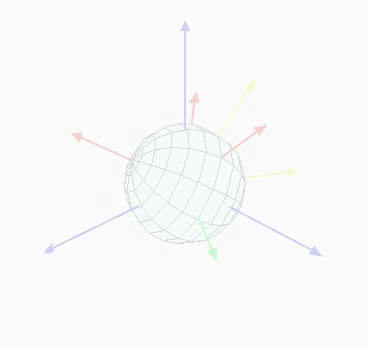
欧拉角的物理意义明确，即分别绕坐标系的三个轴进行旋转，其角度组合对应物体的最终姿态。

b）旋转矩阵

根据线性代数理论，三维空间中的刚体旋转可通过 $3\times 3$ 的正交矩阵表示。例如，绕 $z$ 轴的旋转矩阵形式如下：

c）四元数

四元数是一种数学工具，其形式为 $q=q_0+q_{1}i+q_{2}j+q_{3}k$（其中 $q_0$ 为实部，$q_1、q_2、q_3$ 为虚部，$i、j、k$ 为虚单位且满足特定运算规则），能够优雅且无奇异值地描述三维空间中的刚体旋转。尽管其物理意义不够直观，但在姿态解算中具有显著优势，多数高精度解算算法均采用四元数表示旋转。

以下重点介绍基于四元数的姿态更新方法。

已知当前姿态四元数为 $q_1$，在时间间隔 $\Delta t$ 内角速度为 $\omega$，求下一时刻四元数 $q_2$。

通常采用一阶龙格-库塔法（Euler 积分）进行四元数更新，思路是通过泰勒展开进行一阶近似。计算流程如下：

d）SO(3) 及 so(3)

SO(3) 是特殊正交群，用于描述三维空间中的刚体旋转（所有 $3\times 3$ 正交且行列式为 1 的矩阵构成的集合）；so(3) 是 SO(3) 的李代数，对应三维反对称矩阵空间，用于描述旋转的无穷小变换。

这两种表示方法在主流 MEMS 陀螺仪的姿态解算中应用较少，但在需要对姿态进行求导运算的复杂算法中（如视觉 SLAM 中的姿态优化），需采用李群与李代数的方法描述姿态。例如，旋转矩阵对时间的导数可表示为：

该部分内容较为深入，如需进一步研究可参考高翔博士的《视觉 SLAM 十四讲》。

四、传感器的噪声及去除

传感器的噪声主要分为两类：一类是随机噪声，通常建模为零均值高斯分布；另一类是由测量原理、制造工艺或安装误差导致的固定偏差（系统误差），这类误差是噪声抑制的重点。由于实际应用中对精度要求的差异及高精度校准设备（如高精度转台）的限制，通常仅进行简化的校准操作。

a）陀螺仪

陀螺仪直接测量的是角速度而非角度，需通过积分运算得到角度。积分过程中，固定偏差会不断累积，导致角度漂移。陀螺仪的温漂（温度漂移）是主要误差源之一，其大小与传感器成本正相关，高精度传感器的温漂更小。温漂同时受温度和上电时间影响，不同温度及上电时长下的零偏数值存在差异。

常用的校准方法包括：

1. 上电静止校准：上电后使传感器保持静止一段时间，计算该时段内的平均角速度作为零偏，后续测量值减去该零偏以抵消固定误差；
2. 温度补偿校准：通过实验标定温度与零偏的关系，采用线性插值等方法进行实时补偿；
3. 艾伦方差（Allan Variance）分析：通过艾伦方差法分析零偏与时间的关系，优化校准参数。

对于三轴非正交性、尺度因子不一致等误差，在精度要求较低的场景下可忽略；若需进一步提升精度，可在硬件设计中加入温度控制系统，将传感器温度稳定在 50℃ 左右（需高于常温以避免冷凝影响）。

b）加速度计

加速度计同样存在零偏和尺度因子误差，但由于静止时可直接通过重力加速度解算姿态角（无需积分），零偏对结果的影响较小，而尺度因子误差的影响更为显著。例如，当传感器不同面朝向重力方向时，测量得到的重力加速度幅值存在差异，需通过校准修正。

常用的校准方法为六面校准：将传感器的六个面分别朝向重力方向，记录各方向的测量值，通过最小二乘法等算法计算尺度因子和零偏。对于 MEMS 传感器，若精度要求不高（如无人机应用），仅需正面朝上静止校准一次即可；部分场景（如云台）可根据具体需求设计专用校准流程。

c）磁力计

磁力计的测量误差较大，校准是提升其精度的关键。常用的校准方法包括：

1. 椭球校准法：将磁力计数据导出至 MATLAB，通过拟合测量数据的椭球分布，求解偏差和尺度因子，该方法精度较高但操作复杂，多用于学术研究或写论文；
2. 实时简化校准：多数飞控系统采用单片机实时处理，步骤为：先使传感器头部朝上水平旋转一周，再头部朝下水平旋转一周，记录各轴的最大/最小值；
   • 中值校准：$save.mag\_offset[i]=0.5f\times (max\_t[i]+min\_t[i])$
   • 幅值校准：$save.mag\_gain[i]=safe\_div(200.0f,(0.5f\times (max\_t[i]-min\_t[i])),0)$
3. 高精度校准：若硬件计算能力充足，可采用 LM（Levenberg-Marquardt）算法求解三维偏差和三维尺度因子，具体实现可参考天穹飞控源码。

五、姿态解算原理

IMU 姿态解算是通过融合三个传感器的数据，获取满足以下要求的姿态信息：

1. 滞后效应小；
2. 角度测量准确；
3. 静止时无明显漂移。

实际应用中很多时候都无法满足所有的要求，需根据场景需求权衡各项指标，选择合适的融合策略。

a）陀螺仪

陀螺仪通过积分角速度获取姿态角，但直接积分存在两大问题：

1. 积分误差累积：离散化积分过程中，采样点间的角速度近似会引入误差，示意图如下：
   
   解决方案：采用中值积分替代欧拉积分，减少离散化误差，示意图如下：
   
2. 坐标系转换：陀螺仪测量的角速度基于机体坐标系（Body 系），而姿态解算要求的是世界坐标系（World 系）下的结果，需通过旋转矩阵完成坐标变换。
   
   特殊场景简化：对于无人机等载体，其俯仰角（pitch）和横滚角（roll）通常较小，可近似认为旋转矩阵为单位矩阵，但该简化不适用于云台等大角度运动场景，代码实现中需避免直接积分而忽略坐标变换。

b）加速度计

加速度计的功能为解算俯仰角（pitch）与横滚角（roll），并对陀螺仪积分所得角度进行校准以抑制漂移；常用融合策略采用互补滤波，该方法利用陀螺仪角度短期精度高但存在漂移、加速度计角度无漂移但噪声大的特性，通过滤波算法融合两者的高频与低频成分，最终得到稳定且准确的姿态角。需明确的是，加速度计解算姿态角的前提为载体无额外线加速度（$\mathbf{a}=0$），即测量值仅反映重力加速度的作用，载体静止或匀速直线运动时可满足该条件，而剧烈运动产生的线加速度会引发显著误差。

因此需进行加速度补偿，常用方法包括：

1. 线加速度补偿：通过计算加速度的模长判断载体运动状态，模长越大则降低加速度计的置信权重；
2. 角加速度补偿：通过陀螺仪数据计算角加速度，进而求解切向加速度和法向加速度，对测量值进行补偿；
3. 辅助算法补偿：部分飞控源码采用辅助姿态解算算法实现线加速度补偿（参考天穹飞控源码）。

c）磁力计

磁力计可类比为“电子指南针”，用于校准偏航角（yaw）。其基本计算原理需先对测量数据进行倾斜补偿（消除俯仰角和横滚角对磁场测量的影响），再解算偏航角。

实际工程实现中，为降低计算量，通常会对理论公式进行简化，需结合具体应用场景调整。

六、姿态解算算法

姿态解算算法形式多样，同一算法可采用不同的旋转表示方法（欧拉角、旋转矩阵、四元数）实现。掌握算法的原理是灵活应用的关键，必须深入理解其基本原理，把握其本质特征。尽管这一过程充满挑战，但却是不可或缺的关键步骤。

a）互补滤波

陀螺仪的输出包含高频有效信号和低频漂移误差，加速度计 / 磁力计的输出包含低频有效信号和高频噪声，通过滤波将两者的有效成分叠加，得到兼顾实时性和稳定性的姿态估计结果。

b）AHRS 算法

AHRS（Attitude and Heading Reference System，姿态航向参考系统）是通过传感器数据融合实现姿态和航向估计，常用算法包括 Mahony 算法和 Madgwick 算法：

1. Mahony 算法：计算量小、实时性好，在 Pixhawk 等主流飞控中应用成熟。g

2.madgwick 算法：2012 年开源，效果更好，计算量也更大。g

两种算法的完整推导可参考原始论文：

• Mahony 算法：Nonlinear Complementary Filters on the Special Orthogonal Group；
• Madgwick 算法：An efficient orientation filter for inertial and inertial/magnetic sensor arrays

建议结合算法原始论文与开源飞控源码（如 Pixhawk/PX4、ArduPilot）深入理解推导逻辑与工程实现细节。

c）卡尔曼滤波

卡尔曼滤波是一种基于状态估计的最优滤波算法，广泛应用于多传感器数据融合，通过建立系统模型和观测模型，递归求解最优状态估计值。

对于 IMU 姿态解算，卡尔曼滤波的典型应用方式为：

• 状态量：载体的姿态角（或四元数）、角速度零偏等；
• 预测量：基于「状态转移模型（预测模型）」和陀螺仪的积分结果，得到的下一时刻状态先验估计值；
• 观测量：基于「观测模型」，将加速度计和磁力计解算的姿态角作为观测输入，对预测量进行修正，得到状态后验估计值。

七、云台的特性及要求

7.1 云台特性

1. 姿态角度特性：roll 轴工作时角度偏移量极小，几乎可忽略；而 pitch 轴需具备较大的角度调节范围，以满足目标跟踪或视角调整需求。
2. 安装位置特性：安装点偏离机器人几何中心，导致云台运动时产生的角加速度会对搭载的加速度计输出精度产生显著影响。
3. 动力学干扰特性：机器人启动、停止等运动状态切换时，会产生较大的线加速度，该线加速度会通过机械结构传递至加速度计，形成显著的测量干扰。
4. 姿态零点要求：yaw 轴的零点定位精度对整体系统性能影响较小，无严格限制；而 pitch 轴的零点必须严格保持水平状态，否则会直接影响目标检测、定位等功能的精度。

7.2 姿态解算算法设计与实现

7.2.1 算法选型与融合策略

针对云台姿态解算需求，初始参考 AHRS_Madgwick 算法的框架，将原算法中的互补滤波替换为卡尔曼滤波，以提升静态姿态估计的稳定性。通过实验验证发现：卡尔曼滤波在静态环境下表现出更优的噪声抑制能力，姿态输出更平稳；而原论文中的互补滤波在动态工况下（如云台快速转动、机器人运动状态突变）响应速度更快，姿态跟踪更准确。基于上述特性，采用场景自适应的算法融合策略：根据云台运动状态（静态/动态）切换姿态解算数据来源，静态时采用卡尔曼滤波输出，动态时采用互补滤波输出，以兼顾静态稳定性与动态响应性能。

7.2.2 陀螺仪算法实现要点

陀螺仪相关算法的设计与实现可参考 Madgwick 算法的思路，但建议基于实际需求自主推导实现，以确保算法与硬件平台、应用场景的适配性。具体实现过程中需重点关注以下三点：

1. 算法初始化优化：利用云台出厂校准参数、传感器零偏数据等现有参数，完成算法初始状态的精准配置，避免初始化偏差导致的姿态解算误差累积。
2. 算法模型简化：结合云台的实际运动特性（如 roll 轴角度变化极小、pitch 轴运动范围可控等），在算法推导过程中对动力学模型、观测模型进行合理简化，降低计算复杂度，提升算法实时性，再基于简化后的模型编写对应代码。
3. 误差补偿机制：建立完善的误差校准与补偿体系，包括陀螺仪零偏校准、温度漂移补偿、加速度计测量误差补偿等，通过实验标定误差模型参数，提升姿态解算的整体精度。

---

基于 IMU 的位姿解算

一颗小树x 原创已于 2022-03-14 21:42:17 修改

前言

IMU（Inertial Measurement Unit，惯性测量单元）以牛顿经典力学定律为基本工作原理，由三轴加速度计和三轴陀螺仪作为敏感元件，上电后分别输出载体的线加速度和角速度数据。

在惯性导航领域，通常将固定 IMU 的运动对象称为载体。当载体的位姿（位置与姿态）发生变化时，可通过初始位姿信息，结合 IMU 采样数据完成坐标系间的转换，进而实现对载体位姿、速度等关键运动参数的计算与实时反馈。

IMU 采样数据的解算过程基于惯导解算技术，而定位精度的提升主要依赖于两个方向：一是 IMU 硬件自身测量精度的优化，二是数据融合算法的改进。本文结合相关研究文献，总结了 IMU 位姿解算的方法与典型应用案例，供技术研究与工程实践参考。

一、IMU 特点

民用 IMU 普遍具备体积小、成本低、环境适应性强等优势，但其存在显著的性能局限：纯 IMU 长时间连续工作时，输出数据会出现累积性偏移，解算过程中误差不断叠加，最终导致位姿估计结果失真。

针对这一问题，工程中通常采用多传感器融合策略：在定位场景中，IMU 常与 GPS（全球定位系统）、UWB（超宽带）、视觉相机等传感器组合；在姿态测量场景中，IMU 可与磁力计融合，形成惯性-磁测量单元（Inertial and Magnetic Measurement Unit, IMMU）。IMMU 利用磁力数据和加速度数据解算载体姿态角，对陀螺仪积分得到的姿态结果进行实时滤波，从而提升姿态数据的长期稳定性与精度。

二、IMU 应用

1. 动作捕捉

IMU 动作捕捉是一种基于刚体铰链模型与关节测姿原理的新型动捕方案。通过在人体或机械臂等刚体的关键关节处部署 IMU，实时采集关节运动的角速度与加速度数据，结合运动学模型解算关节姿态，最终重构完整的刚体运动轨迹。该方案无需依赖外部光学设备，适用于室内外复杂环境。

2. 状态判别

基于 IMU 的状态判别需通过机器学习方法实现：首先采集载体在特定状态（如静止、匀速运动、加速运动、碰撞等）下的 IMU 输出数据，构建样本数据集；然后训练分类模型（如支持向量机、神经网络等），使其学习不同状态下的运动特征；最终利用训练好的模型，根据实时 IMU 数据判别载体当前的运动状态。

3. 空间轨迹重建

IMU 在空间轨迹重建中的应用以大范围导航定位为主。通过对 IMU 输出的加速度进行二次积分，结合初始速度与初始位置信息，可解算载体的位置轨迹。该技术广泛应用于机器人自主导航、无人机航迹规划、室内移动设备定位等场景。

4. 组合定位

纯 IMU 定位的累积误差限制了其在长时间、长距离场景中的应用，因此工程中多采用组合导航法，将 IMU 与其他传感器优势互补。常用的组合方案包括：

• IMU/UWB：利用 UWB 的高精度距离测量能力修正 IMU 的累积误差，适用于室内短距离高精度定位；
• IMU/视觉相机：通过视觉传感器获取环境特征点信息，与 IMU 数据融合实现无 GPS 环境下的定位与地图构建（SLAM）；
• IMU/GPS：利用 GPS 的绝对定位能力抑制 IMU 的漂移，同时通过 IMU 弥补 GPS 信号遮挡时的定位中断问题，适用于室外大范围导航；
• 其他组合：如 IMU 与雷达、里程计等传感器的融合，可根据具体应用场景灵活选择。

三、IMU 固定在载体上的位姿解算

当 IMU 固定于某一刚体（如机器人末端执行器、带摄像头的支架、喷枪等）时，由于 IMU 与刚体的相对位置固定，可将 IMU 的运动等同于刚体运动。刚体运动的描述参数是位姿（位置与姿态）随时间的变化规律，其解算过程需遵循捷联惯导解算原理，同时需消除传感器误差与解算过程中引入的误差。

3.1 坐标系转换

位姿解算的首要步骤是完成坐标系转换：

1. 利用机器人运动学参数，将机器人关节坐标转换为 IMU 捷联载体（如喷枪）的初始位姿（初始位置与初始姿态）；
2. IMU 输出的线加速度和角速度数据基于自身坐标系（Body 系），需转换为机器人世界坐标系（World 系） 下的参数，该转换通过姿态矩阵实现；
3. 惯导解算的标准坐标系为当地导航坐标系（如东北天 ENU 坐标系），最终需将 IMU 输出的加速度转换至该坐标系下进行后续解算分析。

坐标系转换关系示意图如下：

3.2 姿态更新

姿态更新是位姿解算的重要环节，流程如下：

1. 将 IMU 输出的 Body 系加速度转换为机器人世界坐标系下的加速度；
2. 基于初始速度对转换后的加速度进行二次积分，得到载体的速度变化量；
3. 结合初始位置信息，最终解算得到载体的实时位置信息。

惯导解算的逻辑包含坐标系转换与姿态更新两个相互关联的环节，整体原理图如下：

3.3 位姿解算注意点

1. 地球自转影响：惯导解算的精确模型需考虑地球自转角速度，但如果研究对象的移动范围远小于地图定位尺度（如室内机器人、小型云台），地球转速、地球自转坐标系等因素对解算结果的影响可忽略；
2. 重力加速度取值：重力加速度的标准值为 $g=9.8{\text{m/s}}^2$，但实际取值建议结合具体地理位置修正。例如，广东省珠三角地区（北纬 $23^{\circ }{2}^{\prime }17.68^{\prime \prime }$）的重力加速度约为 $9.788{\text{m/s}}^2$，精准取值可降低加速度解算误差。

四、姿态表示法

在三维空间中，两个坐标系之间的关系包含 3 个自由度的位置关系和 3 个自由度的姿态关系：

• 位置关系可通过沿 $x$、$y$、$z$ 轴的平移实现原点重合；
• 姿态关系则用于描述坐标系的旋转角度，常用表示方法包括欧拉角、旋转矩阵和单位四元数，三者在满足特定条件时可相互转换。

4.1 欧拉角

欧拉角是姿态描述中最直观的方法，无需正交化处理，在航空、航海等领域应用广泛（通常采用航空次序欧拉角）。

定义：假设存在两个坐标系（坐标系 1 为参考系 $n$，坐标系 2 为载体系 $b$），载体系 $b$ 相对于参考系 $n$ 的任意姿态，均可通过参考系 $n$ 或载体系 $b$ 的三个正交轴依次旋转 3 次获得，这 3 次旋转的角度统称欧拉角。

本文采用 $z$-$y$-$x$ 旋转顺序（偏航-俯仰-横滚），具体定义如下：

1. 第一次绕 $z$ 轴旋转：对应载体的偏航运动，旋转角度称为偏航角（yaw）；
2. 第二次绕 $y$ 轴旋转：对应载体的俯仰运动，旋转角度称为俯仰角（pitch）；
3. 第三次绕 $x$ 轴旋转：对应载体的横滚运动，旋转角度称为横滚角（roll）。

旋转过程示意图如下：

局限性：欧拉角存在万向节死锁（Gimbal Lock） 问题，导致其无法实现全姿态表达。例如，当俯仰角为 $\pm 90^{\circ }$ 时，横滚轴与偏航轴重合，横滚角和偏航角将无法求出，此时无法通过欧拉角唯一确定载体姿态。

4.2 旋转矩阵

旋转矩阵是基于线性代数的姿态表示方法，通过 $3\times 3$ 的正交矩阵描述三维空间中的刚体旋转。

定义：设参考系 $n$ 与载体系 $b$ 原点重合，载体系 $b$ 相对于参考系 $n$ 的旋转可通过旋转矩阵 ${\mathbf{C}}_b^n$ 表示，该矩阵满足以下性质：

• 正交性：${\mathbf{C}}_b^n\cdot ({\mathbf{C}}_b^n{)}^T=\mathbf{I}$（$\mathbf{I}$ 为 $3\times 3$ 单位矩阵）；
• 行列式为 1：$\det ({\mathbf{C}}_b^n)=1$。

物理意义：旋转矩阵 ${\mathbf{C}}_b^n$ 的列向量分别对应载体系 $b$ 的三个坐标轴在参考系 $n$ 中的单位方向向量；行向量分别对应参考系 $n$ 的三个坐标轴在载体系 $b$ 中的单位方向向量。

常见旋转矩阵：

• 绕 $x$ 轴旋转 $\alpha$ 角：
  $${\mathbf{R}}_x(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & -\sin \alpha \\ 0& \sin \alpha & \cos \alpha \end{array}\right]$$
• 绕 $y$ 轴旋转 $\beta$ 角：
  $${\mathbf{R}}_y(\beta )=\left[\begin{array}{ccc}\cos \beta & 0& \sin \beta \\ 0& 1& 0\\ -\sin \beta & 0& \cos \beta \end{array}\right]$$
• 绕 $z$ 轴旋转 $\gamma$ 角：
  $${\mathbf{R}}_z(\gamma )=\left[\begin{array}{ccc}\cos \gamma & -\sin \gamma & 0\\ \sin \gamma & \cos \gamma & 0\\ 0& 0& 1\end{array}\right]$$

复合旋转：若载体系 $b$ 相对于参考系 $n$ 的旋转顺序为 $z$-$y$-$x$（偏航角 $\gamma$、俯仰角 $\beta$、横滚角 $\alpha$），则对应的旋转矩阵为：
$${\mathbf{C}}_b^n={\mathbf{R}}_x(\alpha )\cdot {\mathbf{R}}_y(\beta )\cdot {\mathbf{R}}_z(\gamma )$$

优势与局限：旋转矩阵的物理意义明确，便于坐标系间的向量转换，但存在冗余信息（9 个元素仅需 3 个独立参数描述姿态），且更新过程中需保持正交性，需额外进行正交化处理。

4.3 单位四元数

四元数是由爱尔兰数学家威廉·哈密顿提出的数学工具，其形式为 $\mathbf{q}=q_0+q_1\mathbf{i}+q_2\mathbf{j}+q_3\mathbf{k}$（其中 $q_0$ 为实部，$q_1,q_2,q_3$ 为虚部，$\mathbf{i},\mathbf{j},\mathbf{k}$ 为虚单位，满足 ${\mathbf{i}}^2={\mathbf{j}}^2={\mathbf{k}}^2=\mathbf{ijk}=-1$），单位四元数（$\Vert \mathbf{q}\Vert =\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}=1$）可无奇异地描述三维空间中的刚体旋转。

表示形式：

• 标量-向量形式：$\mathbf{q}=[q_0,{\mathbf{q}}_v{]}^T$，其中 ${\mathbf{q}}_v=[q_1,q_2,q_3{]}^T$ 为虚部向量；
• 轴角形式：若旋转轴为单位向量 $\mathbf{u}=[u_x,u_y,u_z{]}^T$，旋转角为 $\theta$，则单位四元数可表示为：
  $$q_0=\cos \frac{\theta }{2},q_1=u_x\sin \frac{\theta }{2},q_2=u_y\sin \frac{\theta }{2},q_3=u_z\sin \frac{\theta }{2}$$

与旋转矩阵的转换关系：单位四元数 $\mathbf{q}$ 对应的旋转矩阵 ${\mathbf{C}}_b^n$ 为：
$${\mathbf{C}}_b^n=\left[\begin{array}{ccc}1-2q_2^2-2q_3^2& 2q_1{q}_2-2q_0{q}_3& 2q_1{q}_3+2q_0{q}_2\\ 2q_1{q}_2+2q_0{q}_3& 1-2q_1^2-2q_3^2& 2q_2{q}_3-2q_0{q}_1\\ 2q_1{q}_3-2q_0{q}_2& 2q_2{q}_3+2q_0{q}_1& 1-2q_1^2-2q_2^2\end{array}\right]$$

优势：

• 无万向节死锁问题，可实现全姿态表达；
• 冗余信息少于旋转矩阵（4 个元素仅需 3 个独立参数）；
• 姿态更新时的计算量小于旋转矩阵，且无需正交化处理。

应用场景：单位四元数在 IMU 姿态解算、机器人运动学、计算机图形学等领域应用广泛，是多数高精度姿态融合算法的首选姿态表示方法。

参考文献

[1] 黄耀聪. 基于 IMU 的机器人位姿示教技术研究[D]. 广州：广东工业大学，2021.
[2] 严恭敏, 翁浚. 捷联惯导算法与组合导航原理[M]. 西安：西北工业大学出版社，2019.
[3] 高翔, 张涛, 颜沁睿, 等. 视觉 SLAM 十四讲：从理论到实践[M]. 北京：电子工业出版社，2023.
[4] Madgwick S O, Harrison A J L, Vaidyanathan A. Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//2011 IEEE International Conference on Rehabilitation Robotics. IEEE, 2011: 1-7.
[5] Mahony R, Hamel T, Pflimlin J M. Non-linear complementary filters on the special orthogonal group[J]. IEEE Transactions on Automatic Control, 2008, 53(5): 1203-1218.

---

IMU 姿态解算：从 IMU 数据中计算旋转、速度、位置

一点儿也不萌的萌萌 原创已于 2024-03-25 10:16:38 修改

0. 预备知识

a. IMU 测量值定义

IMU 的测量对象是载体相对于地心惯性系（Inertial Frame, i 系） 的运动参数，测量结果通过载体坐标系（Body Frame, b 系） 表示，最终输出两个关键物理量：

• 角速度测量值：${\omega }_{ib}^b$，表示载体坐标系（b 系）相对于惯性系（i 系）的角速度，在 b 系下的投影；
• 线加速度测量值：$a_{ib}^b$，表示载体坐标系（b 系）相对于惯性系（i 系）的线加速度，在 b 系下的投影。

b. IMU 加速度计误差建模

加速度计的测量值包含真值、重力加速度、固定偏差（Bias）和随机噪声，完整建模如下：
$${\tilde{a}}_{ib}^b=a_{ib}^b+g^b+b^a+n^a$$
各参数定义：

• ${\tilde{a}}_{ib}^b$：加速度计最终输出的测量值；
• $a_{ib}^b$：载体线加速度的真值（剔除所有误差项）；
• $g^b$：重力加速度在 b 系下的投影；
• $b^a$：加速度计的固定偏差，短期可视为恒定值，长期会缓慢漂移；
• $n^a$：加速度计的随机测量噪声，建模为零均值高斯噪声（$n^a\sim \mathcal{N}(0,{\sigma }_a^2)$）。

实际应用中，为简化重力加速度的处理（导航系下重力加速度通常表示为 $[0,0,g{]}^T$），常将测量值转换至导航系（Navigation Frame, n 系） 建模：
$${\tilde{a}}_{ib}^b={\mathbf{R}}_{bw}(a_{ib}^w+g^w)+b^a+n^a$$
其中：

• ${\mathbf{R}}_{bw}$ 为 b 系到导航系（w 系，此处与 n 系同义）的旋转矩阵；
• $a_{ib}^w$ 为载体线加速度在导航系下的真值；
• $g^w$ 为重力加速度在导航系下的投影（如东北天坐标系中 $g^w=[0,0,9.8{]}^T{\text{m/s}}^2$）。

c. IMU 陀螺仪误差建模

陀螺仪的测量值包含真值、固定偏差和随机噪声，建模如下：
$${\tilde{\omega }}_{ib}^b={\omega }_{ib}^b+b^g+n^g$$
各参数定义：

• ${\tilde{\omega }}_{ib}^b$：陀螺仪最终输出的测量值；
• ${\omega }_{ib}^b$：载体角速度的真值（剔除所有误差项）；
• $b^g$：陀螺仪的固定偏差，短期恒定，长期缓慢漂移；
• $n^g$：陀螺仪的随机测量噪声，建模为零均值高斯噪声（$n^g\sim \mathcal{N}(0,{\sigma }_g^2)$）。

d. 考虑地球自转的角速度关系

在高精度惯导解算中，需考虑地球自转和导航系相对地球的运动，导航系相对于惯性系的角速度满足：
$${\omega }_{in}^n={\omega }_{ie}^n+{\omega }_{en}^n$$
各参数定义：

• ${\omega }_{in}^n$：导航系（n 系）相对于惯性系（i 系）的角速度，在 n 系下的投影；
• ${\omega }_{ie}^n$：地球相对于惯性系的自转角速度，在 n 系下的投影；
• ${\omega }_{en}^n$：导航系相对于地球的角速度，在 n 系下的投影。

对于 MEMS 级 IMU（低精度），地球自转和导航系运动的影响可忽略，仅在高精度 IMU 解算中需纳入模型。

${\omega }_{ie}^n$ 的计算：
地球自转角速度的标量值为 ${\omega }_{ie}=7.2921151467\times 10^{-5}\text{rad/s}$，在东北天（ENU）导航系下的投影为：
$${\omega }_{ie}^n={\left[\begin{array}{ccc}0& {\omega }_{ie}\cos L& {\omega }_{ie}\sin L\end{array}\right]}^T$$
其中 $L$ 为载体当前位置的地理纬度。

${\omega }_{en}^n$ 的计算：
$${\omega }_{en}^n={\left[\begin{array}{ccc}-\frac{v_N}{R_M+h}& \frac{v_E}{R_N+h}& \frac{v_E}{R_N+h}\tan L\end{array}\right]}^T$$
各参数定义：

• $v_E,v_N$：载体在东北天导航系下的东向、北向速度分量；
• $R_M,R_N$：地球子午圈主曲率半径和卯酉圈主曲率半径；
• $h$：载体的海拔高度；
• $L$：载体当前位置的地理纬度。

地球曲率半径的计算公式（参考《捷联惯导算法与组合导航原理》）：
$$R_N=\frac{R_e}{\sqrt{1-e^2{\sin }^{2}L}},R_M=\frac{R_e(1-e^2)}{(1-e^2{\sin }^{2}L{)}^{\frac{3}{2}}}$$
其中：

• $R_e=6378137\text{m}$（地球赤道半径）；
• $e=0.0818191908$（地球偏心率）。

注：后续推导默认基于 MEMS 级 IMU，忽略地球自转和导航系运动的影响，仅保留解算逻辑。

1. 姿态更新

姿态更新是通过陀螺仪测量的角速度，求解载体姿态随时间的变化，常用旋转矩阵或四元数表示姿态。以下分别介绍惯性系和导航系下的姿态解算方法，参考《捷联惯导算法与组合导航原理》P79。

a. 惯性系下的 IMU 姿态解算

惯性系（i 系）下，姿态旋转矩阵的微分方程为：
$${\dot{\mathbf{C}}}_b^i={\mathbf{C}}_b^i\cdot ({\omega }_{ib}^b\times )$$
其中：

• ${\mathbf{C}}_b^i$ 为 b 系到 i 系的旋转矩阵；
• $({\omega }_{ib}^b\times )$ 表示角速度向量 ${\omega }_{ib}^b$ 对应的反对称矩阵，形式为：
  $$(\omega \times )=\left[\begin{array}{ccc}0& -{\omega }_z& {\omega }_y\\ {\omega }_z& 0& -{\omega }_x\\ -{\omega }_y& {\omega }_x& 0\end{array}\right]$$

对微分方程进行离散化（假设采样时间间隔为 $\Delta t=t_m-t_{m-1}$），可得姿态更新的递推公式：
$${\mathbf{C}}_{b(m)}^i={\mathbf{C}}_{b(m-1)}^i\cdot {\mathbf{C}}_{b(m)}^{b(m-1)}$$
各参数定义：

• ${\mathbf{C}}_{b(m)}^i$：第 $m$ 时刻 b 系到 i 系的旋转矩阵；
• ${\mathbf{C}}_{b(m-1)}^i$：第 $m-1$ 时刻 b 系到 i 系的旋转矩阵；
• ${\mathbf{C}}_{b(m)}^{b(m-1)}$：第 $m-1$ 时刻到第 $m$ 时刻，b 系相对自身的旋转矩阵，由角速度积分得到。

${\mathbf{C}}_{b(m)}^{b(m-1)}$ 的计算：
若载体在 $\Delta t$ 内近似做定轴转动（MEMS IMU 采样频率高，该假设成立），则：
$${\mathbf{C}}_{b(m)}^{b(m-1)}=\exp \left({\int }_{t_{m-1}}^{t_m}{\omega }_{ib}^b(t)dt\right)$$
其中 $\exp (\cdot )$ 为矩阵指数运算，对应旋转矩阵的指数映射。实际工程中，常用数值积分方法近似求解角速度积分，包括：

• 欧拉积分：$\theta ={\omega }_{ib}^b(m-1)\cdot \Delta t$；
• 中值积分：$\theta =\frac{{\omega }_{ib}^b(m-1)+{\omega }_{ib}^b(m)}{2}\cdot \Delta t$；
• 矢量二子样算法：适用于高精度 IMU，参考《捷联惯导算法与组合导航原理》P28~P30。

对于 MEMS 级 IMU，中值积分的精度已足够，积分得到旋转角 $\theta$ 后，通过罗德里格斯公式（Rodrigues’ Formula）计算旋转矩阵：
$$\mathbf{C}=\mathbf{I}+\sin \theta \cdot (\hat{\mathbf{u}}\times )+(1-\cos \theta )\cdot (\hat{\mathbf{u}}\times {)}^2$$
其中 $\hat{\mathbf{u}}$ 为旋转轴单位向量（$\theta =\Vert \theta \Vert$，$\hat{\mathbf{u}}=\theta /\theta$）。

b. 导航系下的 IMU 姿态解算

导航系（n 系）下，姿态旋转矩阵的微分方程为：
$${\dot{\mathbf{C}}}_b^n={\mathbf{C}}_b^n\cdot ({\omega }_{nb}^b\times )$$
其中 ${\omega }_{nb}^b={\omega }_{ib}^b-{\omega }_{in}^b$（${\omega }_{in}^b$ 为导航系相对于惯性系的角速度在 b 系下的投影）。忽略地球自转和导航系运动时，${\omega }_{in}^b=0$，微分方程简化为：
$${\dot{\mathbf{C}}}_b^n={\mathbf{C}}_b^n\cdot ({\omega }_{ib}^b\times )$$

离散化后的姿态更新公式与惯性系下一致：
$${\mathbf{C}}_{b(m)}^n={\mathbf{C}}_{b(m-1)}^n\cdot {\mathbf{C}}_{b(m)}^{b(m-1)}$$
其中 ${\mathbf{C}}_{b(m)}^{b(m-1)}$ 的计算方法与惯性系下相同（中值积分 + 罗德里格斯公式）。

c. 基于四元数的姿态更新

为避免旋转矩阵的正交化维护和万向节死锁问题，工程中更常用四元数表示姿态。四元数的姿态更新微分方程为：
$$\dot{\mathbf{q}}=\frac{1}{2}\mathbf{q}\otimes {\omega }_{ib}^b$$
其中：

• $\mathbf{q}=[q_0,q_1,q_2,q_3{]}^T$ 为单位四元数（$q_0^2+q_1^2+q_2^2+q_3^2=1$）；
• $\otimes$ 表示四元数乘法；
• ${\omega }_{ib}^b$ 表示为纯虚四元数 $[0,{\omega }_x,{\omega }_y,{\omega }_z{]}^T$。

离散化后（中值积分），四元数更新公式为：
$$\mathbf{q}(m)=\mathbf{q}(m-1)\otimes \Delta \mathbf{q}$$
其中 $\Delta \mathbf{q}$ 为 $\Delta t$ 内的姿态变化四元数，由角速度积分得到的旋转角 $\theta$ 转换而来：
$$\Delta \mathbf{q}={\left[\cos \frac{\theta }{2},{\hat{\mathbf{u}}}_x\sin \frac{\theta }{2},{\hat{\mathbf{u}}}_y\sin \frac{\theta }{2},{\hat{\mathbf{u}}}_z\sin \frac{\theta }{2}\right]}^T$$

2. 速度更新

速度更新是通过加速度计测量的线加速度，结合姿态矩阵转换至导航系，积分得到载体速度，参考《捷联惯导算法与组合导航原理》P81。

a. 精确速度微分建模

导航系下，载体速度的微分方程（考虑有害加速度）为：
$${\dot{\mathbf{v}}}_{en}^n={\mathbf{C}}_b^n{f}_{sf}^b-(2{\omega }_{ie}^n+{\omega }_{en}^n)\times {\mathbf{v}}_{en}^n+g^n$$
各参数定义：

• ${\mathbf{v}}_{en}^n$：载体相对于地球的速度，在 n 系下的投影；
• $f_{sf}^b$：加速度计测量的比力（即 ${\tilde{a}}_{ib}^b-b^a-n^a$，剔除偏差和噪声）；
• $-(2{\omega }_{ie}^n+{\omega }_{en}^n)\times {\mathbf{v}}_{en}^n$：有害加速度（科里奥利加速度 + 牵连加速度）；
• $g^n$：重力加速度在 n 系下的投影。

b. 简化版速度微分建模

对于 MEMS 级 IMU，有害加速度的影响可忽略，速度微分方程简化为：
$${\dot{\mathbf{v}}}^n={\mathbf{C}}_b^n{f}_{sf}^b+g^n$$
其中 ${\mathbf{v}}^n$ 为载体在导航系下的速度。

对简化方程进行离散化（中值积分），可得速度更新的递推公式：
$$\mathbf{v}(m)=\mathbf{v}(m-1)+\Delta \mathbf{v}(m)$$
其中 $\Delta \mathbf{v}(m)$ 为 $\Delta t$ 内的速度变化量，计算如下：
$$\Delta \mathbf{v}(m)={\int }_{t_{m-1}}^{t_m}\left({\mathbf{C}}_b^n(t)f_{sf}^b(t)+g^n\right)dt$$

工程中常用中值积分近似：
$$\Delta \mathbf{v}(m)=\frac{1}{2}\left[{\mathbf{C}}_b^n(m-1)f_{sf}^b(m-1)+{\mathbf{C}}_b^n(m)f_{sf}^b(m)\right]\Delta t+g^n\Delta t$$
其中 ${\mathbf{C}}_b^n(m-1)$ 和 ${\mathbf{C}}_b^n(m)$ 分别为第 $m-1$ 时刻和第 $m$ 时刻的姿态旋转矩阵。

3. 位置更新

位置更新是通过速度积分得到载体在导航系下的位置，假设载体在导航系下的位置为 ${\mathbf{p}}^n=[x,y,z{]}^T$，则位置与速度的关系为：
$${\dot{\mathbf{p}}}^n={\mathbf{v}}^n$$

对该方程进行离散化（中值积分），可得位置更新的递推公式：
$$\mathbf{p}(m)=\mathbf{p}(m-1)+{\int }_{t_{m-1}}^{t_m}{\mathbf{v}}^n(t)dt$$

工程中常用中值积分近似（假设速度在 $\Delta t$ 内线性变化）：
$$\mathbf{p}(m)=\mathbf{p}(m-1)+\frac{1}{2}\left[\mathbf{v}(m-1)+\mathbf{v}(m)\right]\Delta t$$

若结合加速度的二次积分，也可表示为：
$$\mathbf{p}(m)=\mathbf{p}(m-1)+\mathbf{v}(m-1)\Delta t+\frac{1}{2}\left({\mathbf{a}}_{avg}^n+g^n\right)\Delta t^2$$
其中 ${\mathbf{a}}_{avg}^n=\frac{1}{2}\left[{\mathbf{C}}_b^n(m-1)f_{sf}^b(m-1)+{\mathbf{C}}_b^n(m)f_{sf}^b(m)\right]$ 为导航系下的平均加速度。

4. 关键说明与工程实现要点

a. 误差抑制

MEMS 级 IMU 的测量误差（零偏、噪声、温漂）会导致姿态、速度、位置的解算结果随时间漂移，工程中需通过以下方法抑制误差：

1. 传感器校准：通过六面校准（加速度计）、椭球校准（磁力计）、艾伦方差校准（陀螺仪零偏）等方法，预先补偿固定偏差；
2. 多传感器融合：结合 GPS、UWB、视觉传感器等提供的绝对测量信息，通过卡尔曼滤波、EKF（扩展卡尔曼滤波）、UKF（无迹卡尔曼滤波）等算法修正 IMU 的累积误差；
3. 算法优化：采用自适应滤波、零速修正（ZUPT）等技术，进一步提升解算精度。

b. 数值稳定性

1. 旋转矩阵正交化：由于数值积分误差，旋转矩阵可能失去正交性，需定期通过 Gram-Schmidt 正交化或归一化处理维护其正交性；
2. 四元数归一化：四元数更新后需进行归一化处理，确保其满足单位四元数条件（$\Vert \mathbf{q}\Vert =1$）；
3. 采样频率选择：MEMS 级 IMU 的采样频率建议不低于 100 Hz，以减小离散化误差。

c. 坐标系一致性

解算过程中需严格保证所有物理量的坐标系一致性：

• 角速度、加速度的测量值均在 b 系下，需通过姿态矩阵转换至 n 系后再进行积分；
• 重力加速度的表示需与导航系定义一致（如东北天坐标系中 $g^n=[0,0,9.8{]}^T$，北东地坐标系中 $g^n=[0,0,-9.8{]}^T$）。

更新 (2024.2.27)：提供一个代码实现，供参考学习：

• eskf-gps-imu-fusion/src/eskf.cpp at · zm0612 · GitHub
  https://github.com/zm0612/eskf-gps-imu-fusion/blob/4b57efe96dbf540fe4b485ee54309ee35fb91d29/src/eskf.cpp#L98

参考文献

[1] 严恭敏, 翁浚. 捷联惯导算法与组合导航原理[M]. 西安：西北工业大学出版社，2019.
[2] 高翔, 张涛, 颜沁睿, 等. 视觉 SLAM 十四讲：从理论到实践[M]. 北京：电子工业出版社，2023.
[3] Madgwick S O, Harrison A J L, Vaidyanathan A. Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//2011 IEEE International Conference on Rehabilitation Robotics. IEEE, 2011: 1-7.
[4] 秦永元. 惯性导航[M]. 北京：科学出版社，2014.
[5] Labbe R. Kalman and Bayesian Filters in Python[M]. 2020._

---

• 姿态控制与工程实现 | 旋转矩阵推导、IMU 姿态解算（篇 1）-优快云博客
  https://blog.youkuaiyun.com/u013669912/article/details/155428694

---

via:

• IMU 原理及姿态融合算法详解_imu 算法-优快云 博客
  https://blog.youkuaiyun.com/RoboChengzi/article/details/97616482
  • How MEMS Accelerometer Gyroscope Magnetometer Work & Arduino Tutorial - YouTube
    https://www.youtube.com/watch?v=eqZgxR6eRjo
  • 如何通俗地解释欧拉角?之后为何要引入四元数? - 知乎
    https://www.zhihu.com/question/47736315
  • 二维与三维旋转变换-优快云 博客(绕其他坐标轴的旋转矩阵表达式)
    https://blog.youkuaiyun.com/csxiaoshui/article/details/65446125
  • Understanding Quaternions3D Game Engine Programming(四元数的运算规则与矩阵运算)
    https://www.3dgep.com/understanding-quaternions/
  • upadte 四元数(1)-----一阶龙格库塔法-优快云 博客
    https://blog.youkuaiyun.com/AASDSADAD/article/details/73080832
  • 视觉 SLAM 中的数学基础 第三篇 李群与李代数 - 半闲居士 - 博客园
    https://www.cnblogs.com/gaoxiang12/p/5137454.html
  • MEMS 惯性传感器误差及校准小白入门 (二)_艾伦方差-优快云 博客
    https://blog.youkuaiyun.com/yandld/article/details/81101984
  • Kalman and Bayesian Filters in Python - Jupyter Notebook Viewer(卡尔曼滤波的直观理解)
    https://nbviewer.jupyter.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb
  • 在无人机姿态解算方面,卡尔曼滤波比互补滤波的优势,从实时性和准确性方面分析? - 知乎(基于互补滤波思想的卡尔曼滤波实现)
    https://www.zhihu.com/question/52030383/answer/146476328
• 基于 IMU 的位姿解算_imu 姿态位置解算原理-优快云 博客
  https://blog.youkuaiyun.com/qq_41204464/article/details/123388193
• IMU 姿态解算,从 IMU 数据中计算旋转､速度､位置,IMU 测量的原理-优快云 博客
  https://blog.youkuaiyun.com/u011341856/article/details/132948044