注:本文为 “仿射变换” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
空间直角坐标转换之仿射变换
3echo Posted on 2008-06-01 16:08
一、引言
在工程开发过程中,坐标系转换是常见问题。目前,关于不同坐标系转换实现方法的相关研究较多,多数实际应用项目均已提出对应的解决方案。两年前,笔者从网络获取《坐标系转换公式》(青岛海洋地质研究所戴勤奋译)一文,该文献对莫洛金斯基-巴德卡斯转换模型、赫尔默特转换模型、布尔莎模型及多项式转换等多种变换模型进行了详细阐述,是坐标系转换领域较为全面的参考资料。
对于常用转换模型,相关从业者通常能够较好地理解。若基于超图、ArcGIS、MapInfo等主流GIS平台进行二次开发,只需准确调用平台提供的接口并梳理清晰逻辑,即可满足用户提出的需求。但在实际应用中,多数开发者对转换模型的内核算法及参数求解过程缺乏深入了解,而相关理论涉及较多数学知识,理解不同模型之间的关联存在一定难度。
二、仿射变换
仿射变换是空间直角坐标转换的一种类型,属于二维坐标到二维坐标的线性变换。该变换能够保持二维图形的“平直线”特性与“平行性”,可通过平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和剪切(Shear)等一系列原子变换复合实现。
仿射变换可采用 3×3 矩阵表示,其最后一行固定为 ( 0 , 0 , 1 ) (0, 0, 1) (0,0,1)。设原坐标为 ( x , y ) (x, y) (x,y),变换后新坐标为 ( x ′ , y ′ ) (x', y') (x′,y′),原坐标与新坐标均视为最后一行为 1 的三维列向量,新列向量通过原列向量左乘变换矩阵得到,具体形式如下:
[ x ′ y ′ 1 ] = [ m 00 m 01 m 02 m 10 m 11 m 12 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix}= \begin{bmatrix} m_{00} & m_{01} & m_{02} \\ m_{10} & m_{11} & m_{12} \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x′y′1 = m00m100m01m110m02m121 xy1
其代数式表达为:
x
′
=
m
00
⋅
x
+
m
01
⋅
y
+
m
02
y
′
=
m
10
⋅
x
+
m
11
⋅
y
+
m
12
x' = m_{00} \cdot x + m_{01} \cdot y + m_{02} \\ y' = m_{10} \cdot x + m_{11} \cdot y + m_{12}
x′=m00⋅x+m01⋅y+m02y′=m10⋅x+m11⋅y+m12
若按旋转、缩放、平移三个分量的复合形式表示,代数式可写为:
X
T
P
=
X
T
0
+
Y
S
P
⋅
sin
θ
Y
+
X
S
P
⋅
cos
θ
X
Y
T
P
=
Y
T
0
+
Y
S
P
⋅
cos
θ
Y
−
X
S
P
⋅
sin
θ
X
X_{TP} = X_{T0} + Y_{SP} \cdot \sin\theta_Y + X_{SP} \cdot \cos\theta_X \\[1em] Y_{TP} = Y_{T0} + Y_{SP} \cdot \cos\theta_Y - X_{SP} \cdot \sin\theta_X
XTP=XT0+YSP⋅sinθY+XSP⋅cosθXYTP=YT0+YSP⋅cosθY−XSP⋅sinθX
(一)仿射变换示意图
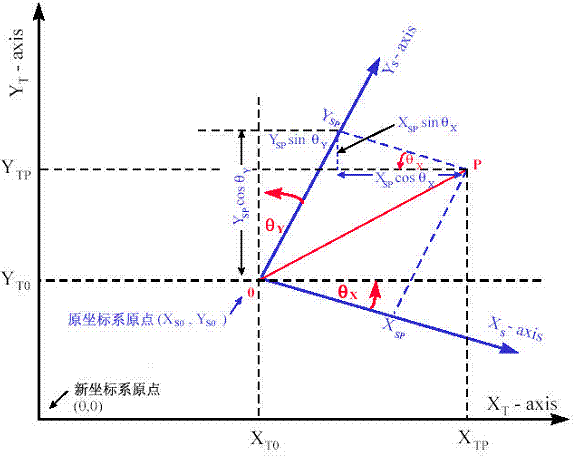
示意图对应关系
- 原坐标系原点为 ( X T 0 , Y T 0 ) (X_{T0}, Y_{T0}) (XT0,YT0),X 轴为 X − a x i s X-axis X−axis,Y 轴为 Y − a x i s Y-axis Y−axis
- 新坐标系原点为 ( 0 , 0 ) (0, 0) (0,0),X 轴为 X T − a x i s X_T-axis XT−axis,Y 轴为 Y T − a x i s Y_T-axis YT−axis
- 变换相关参数包括
X S P X_{SP} XSP(X 方向缩放相关参数)
Y S P Y_{SP} YSP(Y 方向缩放相关参数)
θ X \theta_X θX(X 方向旋转角度)
θ Y \theta_Y θY(Y 方向旋转角度)
X T P X_{TP} XTP(变换后 X 坐标)
Y T P Y_{TP} YTP(变换后 Y 坐标)
(二)典型仿射变换类型
- 平移变换
- 函数定义:
public static AffineTransform getTranslateInstance(double tx, double ty) - 变换说明:将平面内每一点沿 X 方向平移 t x tx tx 单位,沿 Y 方向平移 t y ty ty 单位,变换后点坐标为 ( x + t x , y + t y ) (x + tx, y + ty) (x+tx,y+ty)
- 变换矩阵:
[ 1 0 t x 0 1 t y 0 0 1 ] \begin{bmatrix} 1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{bmatrix} 100010txty1
- 函数定义:
- 备注:平移变换属于刚体变换,不会改变二维图形的形状与大小。刚体变换指变换过程中不会产生形变的理想物体所经历的变换,旋转变换同样属于刚体变换,而缩放变换、剪切变换会改变图形形状。
-
缩放变换
- 函数定义:
public static AffineTransform getScaleInstance(double sx, double sy) - 变换说明:将平面内每一点的横坐标放大(或缩小)至 s x sx sx 倍,纵坐标放大(或缩小)至 s y sy sy 倍
- 变换矩阵:
[ s x 0 0 0 s y 0 0 0 1 ] \begin{bmatrix} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{bmatrix} sx000sy0001
- 函数定义:
-
剪切变换
- 函数定义:
public static AffineTransform getShearInstance(double shx, double shy) - 变换说明:由横向剪切与纵向剪切复合而成
- 变换矩阵:
[ 1 s h x 0 s h y 1 0 0 0 1 ] \begin{bmatrix} 1 & shx & 0 \\ shy & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} 1shy0shx10001 - 备注:剪切变换又称错切变换,其变换特性类似于四边形的不稳定性,例如街边小商店铁拉门的铁条构成菱形并拉动的过程,即为典型的错切变换过程。
- 函数定义:
-
绕原点旋转变换
- 函数定义:
public static AffineTransform getRotateInstance(double theta) - 变换说明:目标图形围绕坐标原点顺时针旋转 θ \theta θ 弧度
- 变换矩阵:
[ cos θ sin θ 0 − sin θ cos θ 0 0 0 1 ] \begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} cosθ−sinθ0sinθcosθ0001
- 函数定义:
-
绕指定点旋转变换
- 函数定义:
public static AffineTransform getRotateInstance(double theta, double x, double y) - 变换说明:目标图形以点 ( x , y ) (x, y) (x,y) 为旋转轴心顺时针旋转 θ \theta θ 弧度
- 变换矩阵:
[ cos θ sin θ y − x sin θ − y cos θ − sin θ cos θ x − x cos θ + y sin θ 0 0 1 ] \begin{bmatrix} \cos\theta & \sin\theta & y - x\sin\theta - y\cos\theta \\ -\sin\theta & \cos\theta & x - x\cos\theta + y\sin\theta \\ 0 & 0 & 1 \end{bmatrix} cosθ−sinθ0sinθcosθ0y−xsinθ−ycosθx−xcosθ+ysinθ1 - 备注:该变换相当于两次平移变换与一次原点旋转变换的复合,复合过程的矩阵运算如下:
[ 1 0 − x 0 1 − y 0 0 1 ] [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] [ 1 0 x 0 1 y 0 0 1 ] \begin{bmatrix} 1 & 0 & -x \\ 0 & 1 & -y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & x \\ 0 & 1 & y \\ 0 & 0 & 1 \end{bmatrix} 100010−x−y1 cosθsinθ0−sinθcosθ0001 100010xy1
- 函数定义:
三、仿射变换四参数求解
(一)C# 自定义函数实现求解
- 求解旋转参数(Rotation)
/// <summary>
/// 获取旋转角度
/// </summary>
/// <param name="fromPoint1">源点 1</param>
/// <param name="toPoint1">目标点 1</param>
/// <param name="fromPoint2">源点 2</param>
/// <param name="toPoint2">目标点 2</param>
/// <returns>返回旋转角度</returns>
private double GetRotation(CoordPoint fromPoint1, CoordPoint toPoint1, CoordPoint fromPoint2, CoordPoint toPoint2)
{
double a = (toPoint2.Y - toPoint1.Y) * (fromPoint2.X - fromPoint1.X) - (toPoint2.X - toPoint1.X) * (fromPoint2.Y - fromPoint1.Y);
double b = (toPoint2.X - toPoint1.X) * (fromPoint2.X - fromPoint1.X) + (toPoint2.Y - toPoint1.Y) * (fromPoint2.Y - fromPoint1.Y);
if (Math.Abs(b) > 0)
{
return Math.Tan(a / b);
}
else
{
return Math.Tan(0);
}
}
- 求解缩放比例参数(Scale)
/// <summary>
/// 获取缩放比例因子
/// </summary>
/// <param name="fromPoint1">源点 1</param>
/// <param name="toPoint1">目标点 1</param>
/// <param name="fromPoint2">源点 2</param>
/// <param name="toPoint2">目标点 2</param>
/// <param name="rotation">旋转角度</param>
/// <returns>返回缩放比例因子</returns>
private double GetScale(CoordPoint fromPoint1, CoordPoint toPoint1, CoordPoint fromPoint2, CoordPoint toPoint2, double rotation)
{
double a = toPoint2.X - toPoint1.X;
double b = (fromPoint2.X - fromPoint1.X) * Math.Cos(rotation) - (fromPoint2.Y - fromPoint1.Y) * Math.Sin(rotation);
if (Math.Abs(b) > 0)
{
return a / b;
}
else
{
return 0;
}
}
- 求解 X 方向偏移距离参数(XTranslate)
/// <summary>
/// 得到 X 方向偏移量
/// </summary>
/// <param name="fromPoint1">源点 1</param>
/// <param name="toPoint1">目标点 1</param>
/// <param name="rotation">旋转角度</param>
/// <param name="scale">缩放因子</param>
/// <returns>返回 X 方向偏移量</returns>
private double GetXTranslation(CoordPoint fromPoint1, CoordPoint toPoint1, double rotation, double scale)
{
return (toPoint1.X - scale * (fromPoint1.X * Math.Cos(rotation) - fromPoint1.Y * Math.Sin(rotation)));
}
- 求解 Y 方向偏移距离参数(YTranslate)
/// <summary>
/// 得到 Y 方向偏移量
/// </summary>
/// <param name="fromPoint1">源点 1</param>
/// <param name="toPoint1">目标点 1</param>
/// <param name="rotation">旋转角度</param>
/// <param name="scale">缩放因子</param>
/// <returns>返回 Y 方向偏移量</returns>
private double GetYTranslation(CoordPoint fromPoint1, CoordPoint toPoint1, double rotation, double scale)
{
return (toPoint1.Y - scale * (fromPoint1.X * Math.Sin(rotation) + fromPoint1.Y * Math.Cos(rotation)));
}
(二)C# + AE 求解
/// <summary>
/// 从控制点定义仿射变换程式
/// </summary>
/// <param name="pFromPoints">源控制点</param>
/// <param name="pToPoints">目标控制点</param>
/// <returns>返回变换定义</returns>
private ITransformation GetAffineTransformation(IPoint[] pFromPoints, IPoint[] pToPoints)
{
// 实例化仿射变换对象
IAffineTransformation2D tAffineTransformation = new AffineTransformation2DClass();
// 从源控制点定义参数
tAffineTransformation.DefineFromControlPoints(ref pFromPoints, ref pToPoints);
// 查询引用接口
ITransformation tTransformation = tAffineTransformation as ITransformation;
return tTransformation;
}
四、空间对象转换
在求解得到仿射变换相关参数后,利用变换公式对坐标点进行转换的操作相对简便,以下为转换示例代码:
/// <summary>
/// 转换空间点
/// </summary>
/// <param name="pPoint">待转换点</param>
/// <returns>返回转换后的点</returns>
private IGeometry TransformPoint(IPoint pPoint)
{
// 采用相似变换模型(四参数变换模型)
// 变换公式:X = a x - b y + c;Y = b x + a y + d
double A = this.m_Scale * Math.Cos(this.m_RotationAngle);
double B = this.m_Scale * Math.Sin(this.m_RotationAngle);
IPoint tPoint = new PointClass();
tPoint.X = A * pPoint.X - B * pPoint.Y + this.m_DX;
tPoint.Y = B * pPoint.X + A * pPoint.Y + this.m_DY;
return tPoint;
}
五、总结
本文围绕空间直角坐标转换中的仿射变换展开阐述,详细介绍了仿射变换的基本原理、典型类型及数学表达形式,提供了仿射变换四参数的两种求解实现方法(C# 自定义函数求解与 C# + AE 求解),并给出了空间点坐标转换的示例代码。对于 ArcGIS 平台用户,可直接调用平台自带接口完成空间坐标转换操作。
在本文撰写过程中,笔者对坐标变换各类模型的理解尚未完全深入,仍存在部分待解决的问题,例如如何利用最小二乘法公式求解相关参数等,恳请相关领域研究者与从业者给予指导。
六、备注
(一)补充变换公式
-
X
=
a
x
+
b
y
+
c
X = a x + b y + c
X=ax+by+c
Y = − b x + a y + f Y = -b x + a y + f Y=−bx+ay+f -
X
=
a
x
−
b
y
+
c
X = a x - b y + c
X=ax−by+c
Y = b x + a y + d Y = b x + a y + d Y=bx+ay+d
(二)参考资料
- 《坐标系转换公式》.(青岛海洋地质研究所 戴勤奋 译)
- Java 文档帮助之 AffineTransform
- ESRI 开发文档
仿射变换(Affine Transformation)在 2D 和 3D 坐标下的变换矩阵、性质及齐次坐标系(Homogeneous Coordinates)的应用
kkyson 编辑于 2022-02-12 20:19
前注
近期从零开始学习计算机图形学,以 GAMES101 闫令琪老师的图形学课程作为入门材料。课程中,闫老师采用深入浅出、通俗易懂的讲解方式,使此前诸多疑惑得以解答,同时也意识到大一阶段线性代数知识的薄弱。本文为 B 站版本课程第三节课中“仿射变换及齐次坐标系”部分的学习笔记,在整理巩固课程知识的基础上,结合了其他参考资料及自主推导计算,旨在便于个人记忆与理解。需说明的是,笔记内容未完全遵循课程讲解顺序,而是根据个人认知逻辑进行编排。
一、仿射变换定义
① 定义表述
通过查阅多篇英文资料,Brilliant 与 Wiki 上的定义表述较为易懂,其英文原文如下:
An affine transformation is a type of geometric transformation which preserves collinearity (if a collection of points sits on a line before the transformation, they all sit on a line afterwards) and the ratios of distances between points on a line.
仿射变换(Affine Transformation) 是一类几何变换,它保持共线性(若变换前一组点共线,则变换后这些点仍共线)以及直线上点与点之间的距离比例不变。
该定义的关键词为 transformation(变换)、collinearity(共线性)及 ratios of distances(距离比例)。仿射变换是几何变换的一种,常见的几何变换还包括:
- 刚体变换:图形形状与任意两点间距离保持不变,包含平移和旋转;
- 仿射变换:保持共线性与线上点的距离比例不变(本文讨论内容);
- 投影变换:变换后图形的平行关系可能改变,共线性不一定保持;
- 非线性变换:因相关知识储备有限,暂不展开说明。
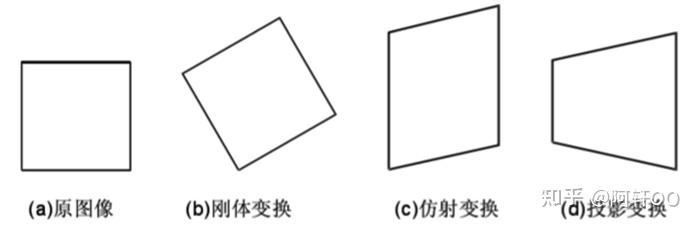
图片来自博客园 侵权删
关于仿射变换的性质补充说明:
- 共线性保持:不仅限于直线,对二次曲线的映射映射为二次曲线;
- 距离比例保持:仿射变换不保持线段的绝对距离,但保持线段上点的比例分割关系。
二、仿射变换的包含内容
课程中重点讲解的仿射变换类型包括平移(Translation)、旋转(Rotation)、缩放(Scaling)、剪切(Shearing),此外对称(Mirroring)、反射(Reflection)等也属于仿射变换的范畴。
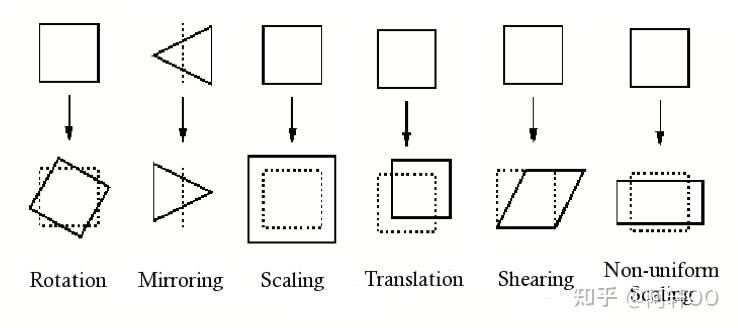
几种主要的仿射变换类型
以下首先介绍 2D 坐标系下上述几种变换的具体形式及对应变换矩阵,其中平移变换将结合齐次坐标系的概念一同引出;3D 坐标系下的仿射矩阵将在文末给出。
约定:变换前图像上任意一点的坐标记为 ( x , y ) (x, y) (x,y),变换后对应点的坐标记为 ( x ′ , y ′ ) (x', y') (x′,y′)
① 缩放变换
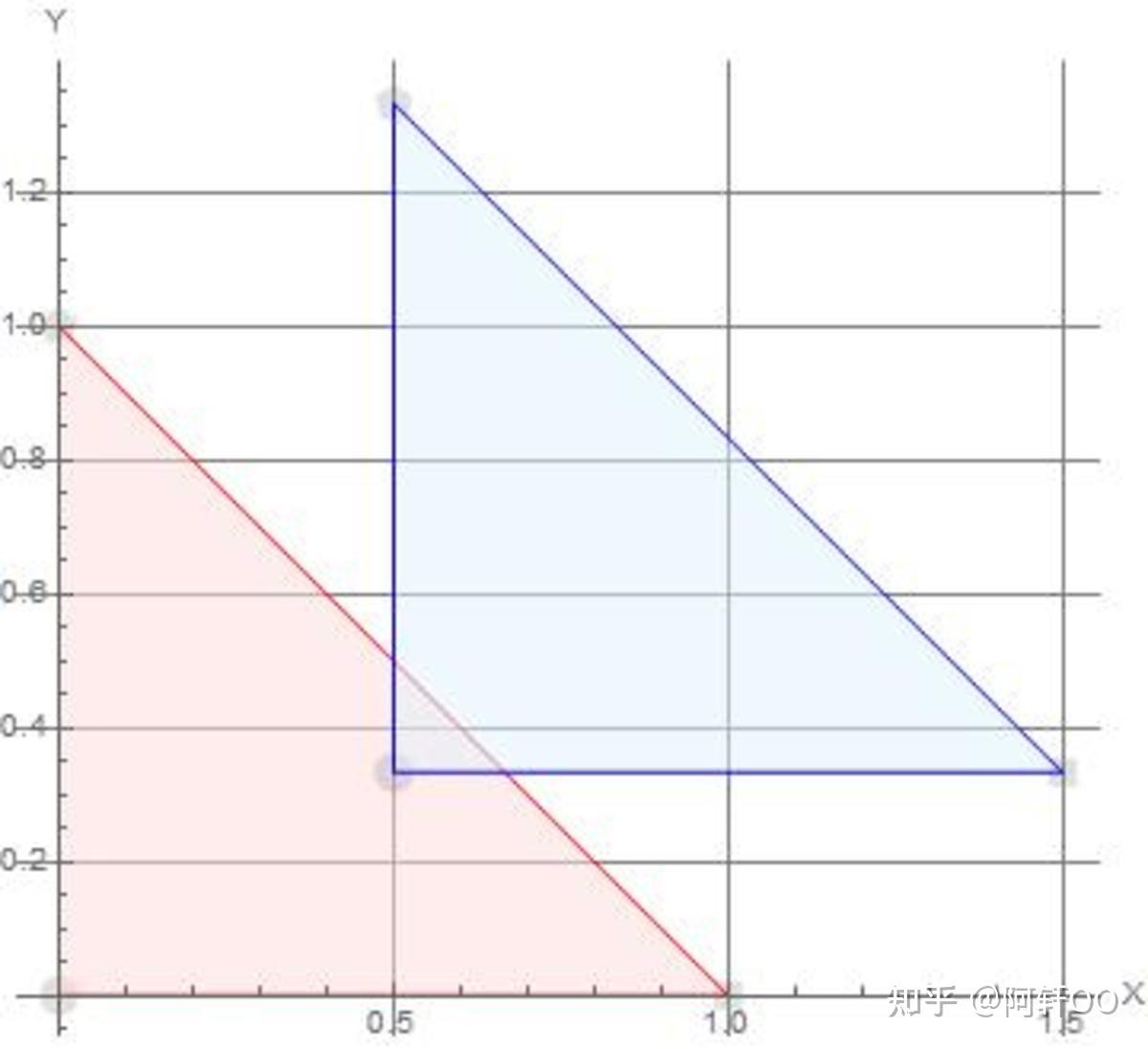
以 Brilliant 网站的示意图为例,图中三角形的纵坐标 y y y 乘以系数 0.5 0.5 0.5,即变为原来的一半。
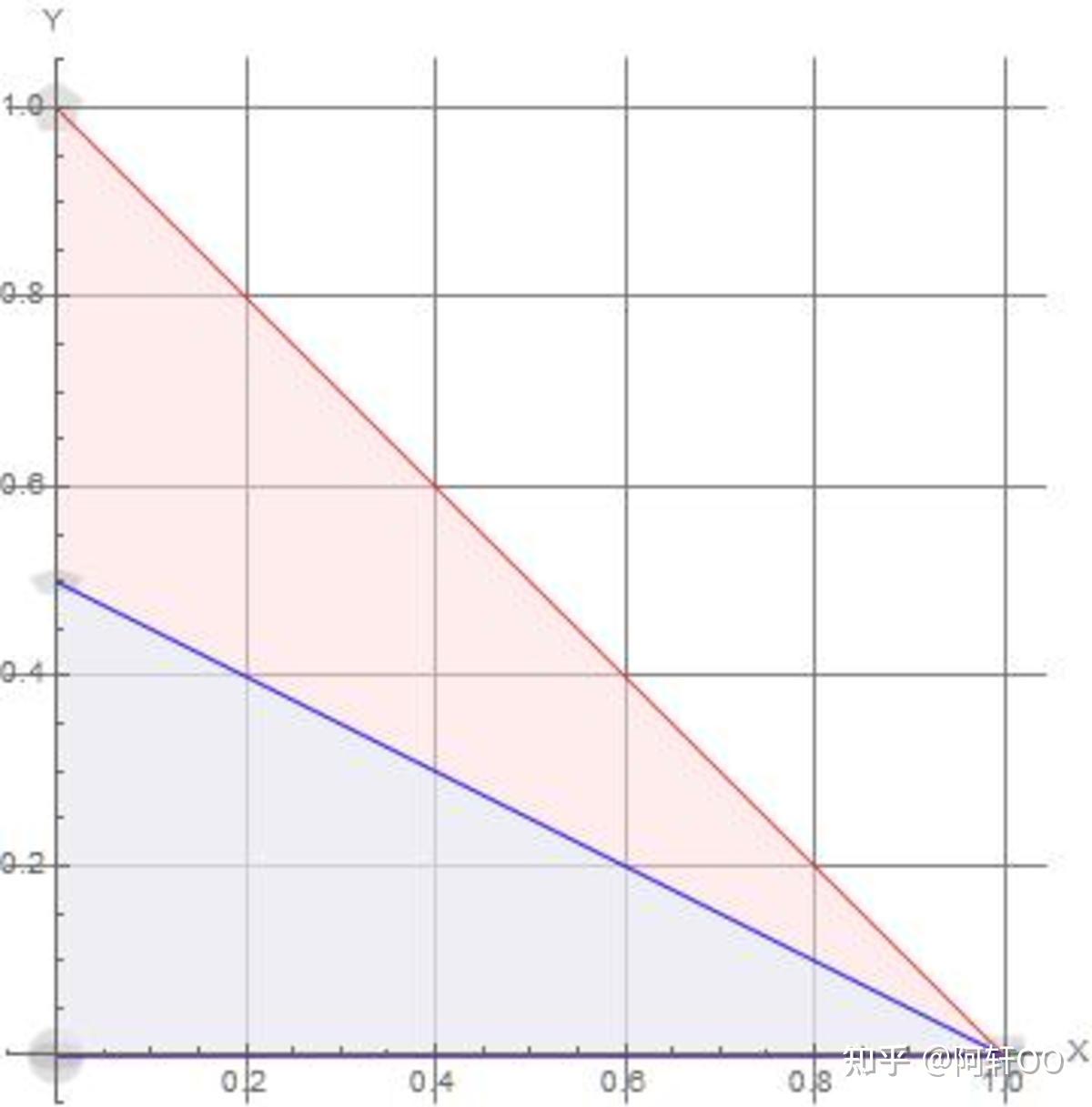
红色为原图形,蓝色为变换后图形
具体变换关系及矩阵形式如下:
{
x
′
=
x
y
′
=
1
2
y
⟹
[
x
′
y
′
]
=
[
1
0
0
1
2
]
[
x
y
]
\begin{cases} x' = x \\ y' = \frac{1}{2}y \end{cases} \implies \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & \frac{1}{2} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
{x′=xy′=21y⟹[x′y′]=[10021][xy]
推广至一般形式,设
x
x
x 方向缩放系数为
s
x
s_x
sx,
y
y
y 方向缩放系数为
s
y
s_y
sy,则变换关系为:
{
x
′
=
s
x
x
y
′
=
s
y
y
⟹
[
x
′
y
′
]
=
[
s
x
0
0
s
y
]
[
x
y
]
\begin{cases} x' = s_x x \\ y' = s_y y \end{cases} \implies \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
{x′=sxxy′=syy⟹[x′y′]=[sx00sy][xy]
② 旋转变换
默认旋转中心为坐标原点 ( 0 , 0 ) (0, 0) (0,0),绕任意点的旋转方式将在后续补充。
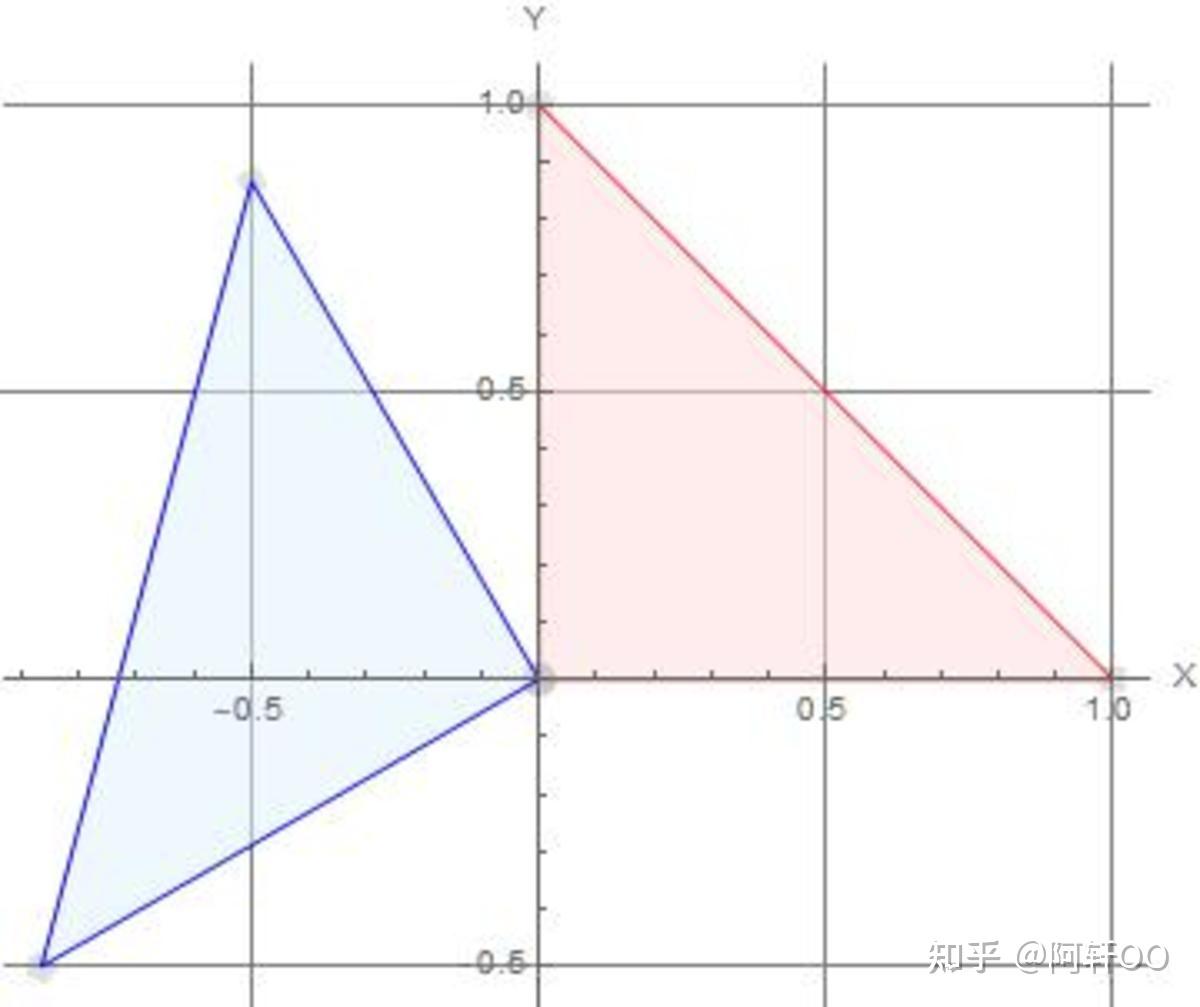
红色为原图形,蓝色为变换后图形
设旋转角度为
θ
\theta
θ,其变换矩阵如下:
[
x
′
y
′
]
=
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
[
x
y
]
\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
[x′y′]=[cosθsinθ−sinθcosθ][xy]
矩阵推导过程
课程中通过特殊点验证的方式证明了该矩阵的有效性,但未给出一般性推导。因为公理对于所有符合条件的点都适合,那么对于特殊点也应该符合。以下结合三角函数公式进行推导:
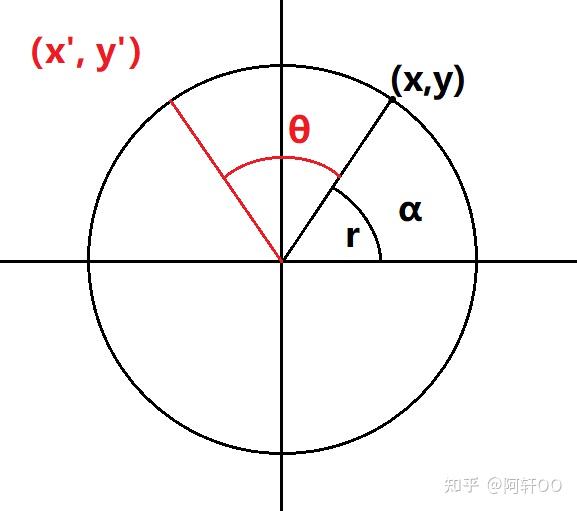
如图所示,设任意点
(
x
,
y
)
(x, y)
(x,y) 与原点的连线为半径
r
r
r,该连线与
x
x
x 轴的夹角为
α
\alpha
α,旋转角度为
θ
\theta
θ。根据三角函数定义,原坐标可表示为:
{
x
=
r
cos
α
y
=
r
sin
α
⟹
(
x
,
y
)
=
(
r
cos
α
,
r
sin
α
)
\begin{cases} x = r \cos\alpha \\ y = r \sin\alpha \end{cases} \implies (x, y) = (r \cos\alpha, r \sin\alpha)
{x=rcosαy=rsinα⟹(x,y)=(rcosα,rsinα)
旋转后,新坐标
(
x
′
,
y
′
)
(x', y')
(x′,y′) 与
x
x
x 轴的夹角变为
α
+
θ
\alpha + \theta
α+θ,该点可表示为:
{
x
′
=
r
cos
(
α
+
θ
)
y
′
=
r
sin
(
α
+
θ
)
\begin{cases} x' = r \cos(\alpha + \theta) \\ y' = r \sin(\alpha + \theta) \end{cases}
{x′=rcos(α+θ)y′=rsin(α+θ)
根据三角函数和角公式:
cos
(
α
+
θ
)
=
cos
α
cos
θ
−
sin
α
sin
θ
sin
(
α
+
θ
)
=
sin
α
cos
θ
+
cos
α
sin
θ
\cos(\alpha + \theta) = \cos\alpha \cos\theta - \sin\alpha \sin\theta \\ \sin(\alpha + \theta) = \sin\alpha \cos\theta + \cos\alpha \sin\theta
cos(α+θ)=cosαcosθ−sinαsinθsin(α+θ)=sinαcosθ+cosαsinθ
将原坐标表达式代入上式,化简可得:
x
′
=
r
cos
α
cos
θ
−
r
sin
α
sin
θ
=
x
cos
θ
−
y
sin
θ
y
′
=
r
sin
α
cos
θ
+
r
cos
α
sin
θ
=
x
sin
θ
+
y
cos
θ
x' = r \cos\alpha \cos\theta - r \sin\alpha \sin\theta = x \cos\theta - y \sin\theta \\ y' = r \sin\alpha \cos\theta + r \cos\alpha \sin\theta = x \sin\theta + y \cos\theta
x′=rcosαcosθ−rsinαsinθ=xcosθ−ysinθy′=rsinαcosθ+rcosαsinθ=xsinθ+ycosθ
整理为矩阵形式:
[
x
′
y
′
]
=
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
[
x
y
]
\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
[x′y′]=[cosθsinθ−sinθcosθ][xy]
③ 剪切变换(Shearing)
剪切变换的几何意义类似四边形的不稳定性,表现为图形沿某一方向的平移变形。设 a a a 为 x x x 方向剪切系数, b b b 为 y y y 方向剪切系数,其变换矩阵分为以下三种情况:
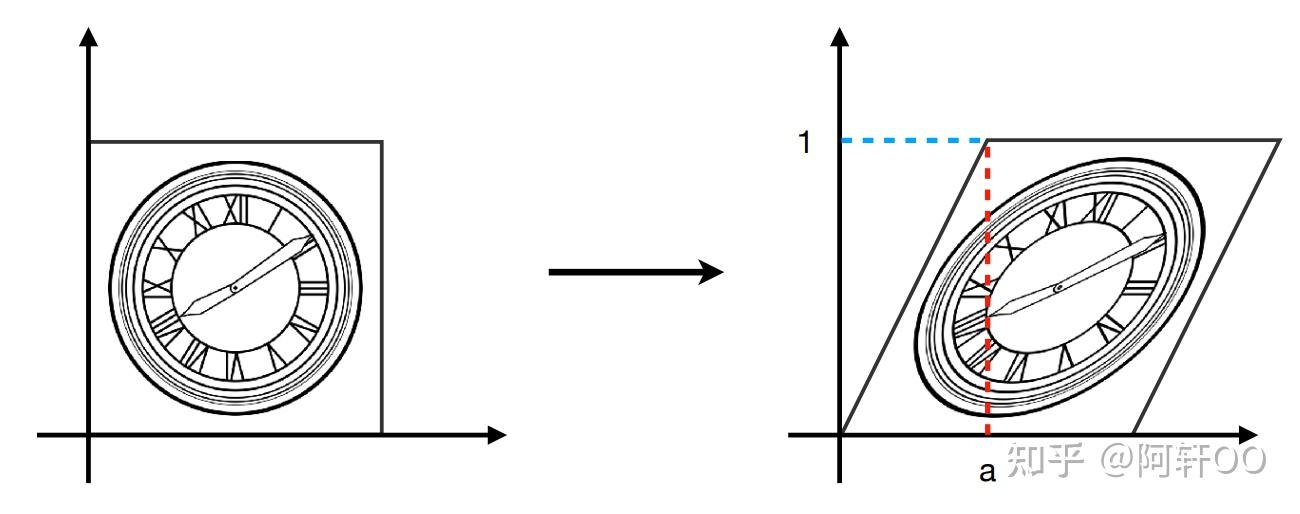
-
沿 x x x 轴横向剪切:
[ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[10a1][xy] -
沿 y y y 轴纵向剪切:
[ x ′ y ′ ] = [ 1 0 b 1 ] [ x y ] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ b & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[1b01][xy] -
x x x 和 y y y 方向均剪切:
[ x ′ y ′ ] = [ 1 a b 1 ] [ x y ] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & a \\ b & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[1ba1][xy]
④ 对称变换
对称变换的矩阵形式较为简单,以下结合示意图给出对应矩阵(无需额外推导):
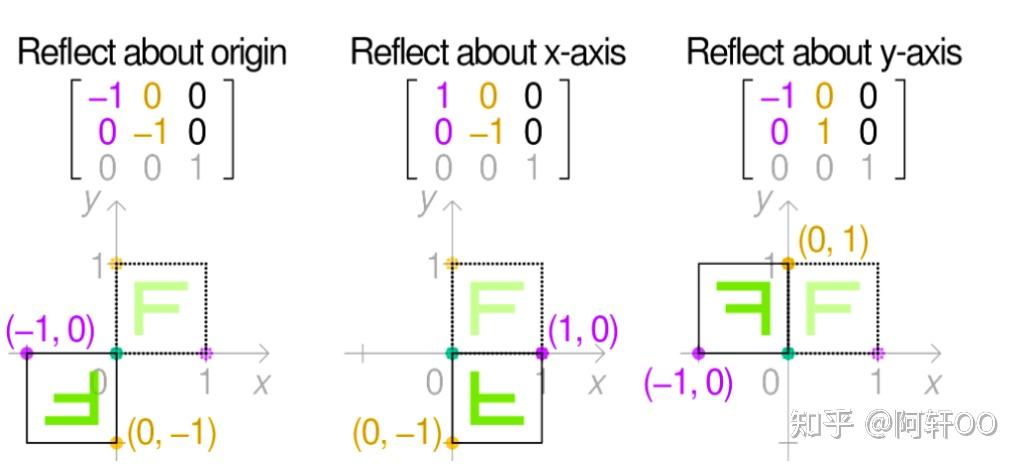
⑤ 线性变换的统一表示
除平移变换外,上述所有仿射变换均可表示为以下线性变换形式:
{
x
′
=
a
x
+
b
y
y
′
=
c
x
+
d
y
⟹
[
x
′
y
′
]
=
[
a
b
c
d
]
[
x
y
]
⟹
x
′
=
M
x
\begin{cases} x' = a x + b y \\ y' = c x + d y \end{cases} \implies \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \implies \mathbf{x}' = \mathbf{M} \mathbf{x}
{x′=ax+byy′=cx+dy⟹[x′y′]=[acbd][xy]⟹x′=Mx
其中, x \mathbf{x} x 和 x ′ \mathbf{x}' x′ 分别表示原坐标向量和变换后坐标向量, M \mathbf{M} M 表示变换矩阵。
多个变换矩阵可通过对原向量进行左乘一个 or 多个变换矩阵的方式进行得到,其实矩阵乘法可以合并为一个等效矩阵,因为多次变换可通过单次矩阵乘法实现。上述变换均属于线性变换(Linear Transforms)。
三、齐次坐标系的引入
① 平移变换的特殊性
平移变换无法用上述线性变换 x ′ = M x \mathbf{x}' = \mathbf{M} \mathbf{x} x′=Mx 表示,这是引入齐次坐标系的原因。
设
x
x
x 方向平移分量为
t
x
t_x
tx,
y
y
y 方向平移分量为
t
y
t_y
ty,则平移变换的坐标关系为:
{
x
′
=
x
+
t
x
y
′
=
y
+
t
y
⟹
[
x
′
y
′
]
=
[
a
b
c
d
]
[
x
y
]
+
[
t
x
t
y
]
\begin{cases} x' = x + t_x \\ y' = y + t_y \end{cases} \implies \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}
{x′=x+txy′=y+ty⟹[x′y′]=[acbd][xy]+[txty]
该式包含线性项与常数项,无法简化为 x ′ = M x \mathbf{x}' = \mathbf{M} \mathbf{x} x′=Mx 的形式,因此平移变换不属于线性变换。为实现所有仿射变换的统一表示,需引入齐次坐标系。
② 齐次坐标系与坐标转换
齐次坐标系通过增加一个维度(引入参数
w
w
w),将 2D 坐标
(
x
,
y
)
(x, y)
(x,y) 扩展为 3D 形式
(
x
,
y
,
w
)
(x, y, w)
(x,y,w)。对于 2D 平面上的点,通常取
w
=
1
w = 1
w=1,其与笛卡尔坐标系的转换关系如下:
[
x
y
w
]
⇒
(
2
D
)
[
x
/
w
y
/
w
1
]
(
w
≠
0
)
\begin{bmatrix} x \\ y \\ w \end{bmatrix} \Rightarrow (2\text{D}) \begin{bmatrix} {x}/{w} \\ {y}/{w} \\ 1 \end{bmatrix} \quad (w \neq 0)
xyw
⇒(2D)
x/wy/w1
(w=0)
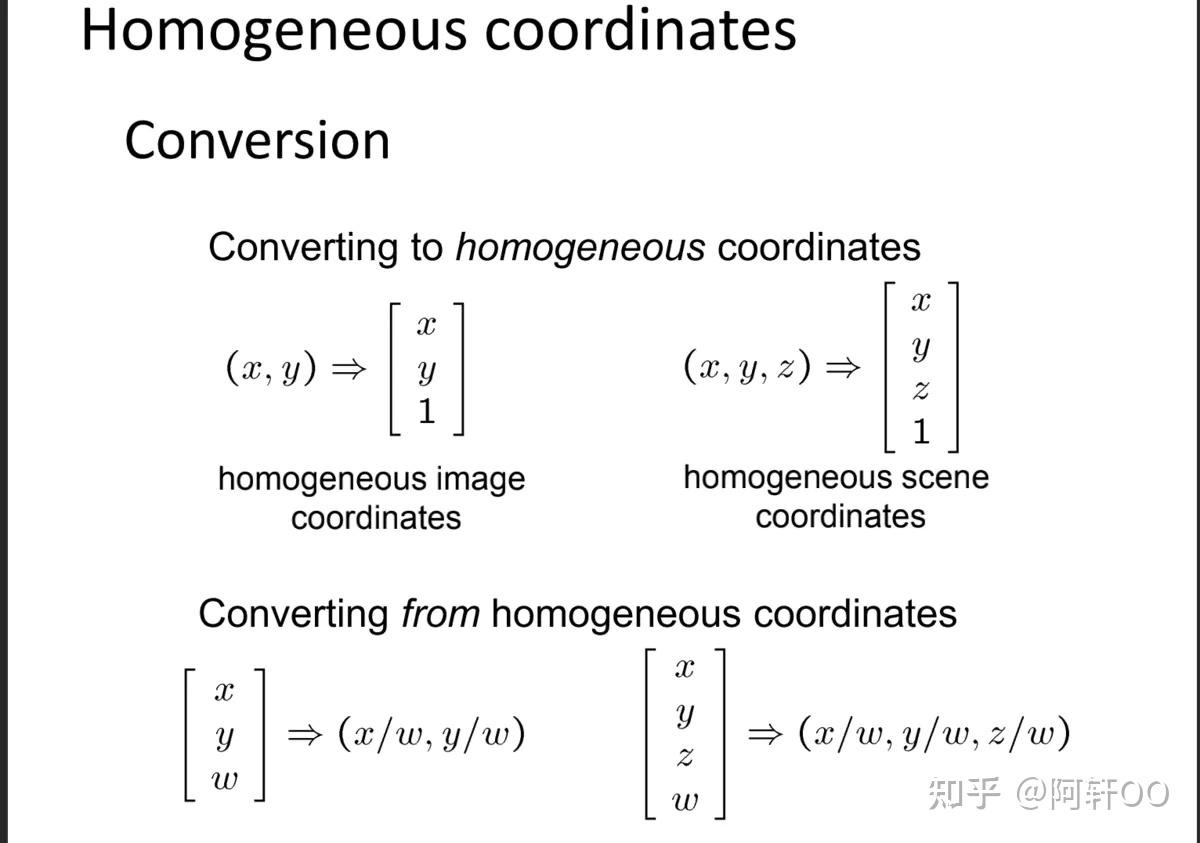
引入齐次坐标系后,平移变换可表示为矩阵乘法形式:
[
x
′
y
′
w
′
]
=
[
1
0
t
x
0
1
t
y
0
0
1
]
[
x
y
1
]
=
[
x
+
t
x
y
+
t
y
1
]
\begin{bmatrix} x' \\ y' \\ w' \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + t_x \\ y + t_y \\ 1 \end{bmatrix}
x′y′w′
=
100010txty1
xy1
=
x+txy+ty1
③ 仿射变换的两种表示方式对比
笛卡尔坐标系下的表示
仿射变换可分解为线性变换与平移变换的叠加:
仿射变换 = 线性变换 + 平移变换 ⏞ 仿射变换数学表达 [ x ′ y ′ ] = [ a b c d ] [ x y ] + [ t x t y ] \overbrace{\textbf{仿射变换 = 线性变换 + 平移变换}}^{\text{仿射变换数学表达}} \\[1em] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix} 仿射变换 = 线性变换 + 平移变换 仿射变换数学表达[x′y′]=[acbd][xy]+[txty]
齐次坐标系下的表示
所有仿射变换均可统一表示为 3×3 矩阵与齐次坐标向量的乘法,变换矩阵的最后一行固定为
[
0
,
0
,
1
]
[0, 0, 1]
[0,0,1]:
[
x
′
y
′
1
]
=
[
a
b
t
x
c
d
t
y
0
0
1
]
[
x
y
1
]
\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
x′y′1
=
ac0bd0txty1
xy1
常见仿射变换的齐次矩阵形式
-
缩放变换(Scaling):
[ s x 0 0 0 s y 0 0 0 1 ] \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} sx000sy0001 -
旋转变换(Rotation):
[ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} cosθsinθ0−sinθcosθ0001 -
平移变换(Translation):
[ 1 0 t x 0 1 t y 0 0 1 ] \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} 100010txty1 -
剪切变换(Shearing):
[ 1 a 0 b 1 0 0 0 1 ] \begin{bmatrix} 1 & a & 0 \\ b & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} 1b0a10001
四、3D 坐标系下的仿射变换矩阵及矩阵性质
① 缩放变换和平移变换矩阵
3D 坐标系下的缩放与平移变换矩阵可通过 2D 情况类比推导得出,其齐次坐标形式(4×4 矩阵)如下:
Scale
S
(
s
x
,
s
y
,
s
z
)
=
(
s
x
0
0
0
0
s
y
0
0
0
0
s
z
0
0
0
0
1
)
\mathbf{S}(s_x, s_y, s_z) = \begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}
S(sx,sy,sz)=
sx0000sy0000sz00001
Translation
T
(
t
x
,
t
y
,
t
z
)
=
(
1
0
0
t
x
0
1
0
t
y
0
0
1
t
z
0
0
0
1
)
\mathbf{T}(t_x, t_y, t_z) = \begin{pmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{pmatrix}
T(tx,ty,tz)=
100001000010txtytz1
缩放矩阵的性质
-
对称性:缩放矩阵为对称矩阵(正矩阵),满足 S ( s x , s y , s z ) = S T S_{(s_{x},s_{y},s_{z})}=S^T S(sx,sy,sz)=ST,即 S = S T \mathbf{S} = \mathbf{S}^T S=ST( S T \mathbf{S}^T ST 表示矩阵 S \mathbf{S} S 的转置);
-
逆矩阵:缩放矩阵的逆矩阵为各缩放系数取倒数后的矩阵:
S − 1 = [ 1 / s x 0 0 0 0 1 / s y 0 0 0 0 1 / s z 0 0 0 0 1 ] \mathbf{S}^{-1} = \begin{bmatrix} 1/s_x & 0 & 0 & 0 \\ 0 & 1/s_y & 0 & 0 \\ 0 & 0 & 1/s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} S−1= 1/sx00001/sy00001/sz00001 同样也是对称矩阵,衍生性质:
- 缩放矩阵的转置矩阵等于其本身;
- 缩放矩阵的逆转置矩阵等于其逆矩阵。
② 旋转变换矩阵
正交矩阵的定义
旋转矩阵是典型的正交矩阵,正交矩阵的定义为:矩阵的转置等于其逆矩阵,即 R T = R − 1 \mathbf{R}^T = \mathbf{R}^{-1} RT=R−1。
2D 旋转矩阵的正交性验证
已知 2D 旋转矩阵用笛卡尔坐标表示为:
R
θ
=
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
\mathbf{R}_\theta = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}
Rθ=[cosθsinθ−sinθcosθ]
其逆矩阵为绕原点旋转
−
θ
-\theta
−θ 的矩阵:
R
−
θ
=
[
cos
(
−
θ
)
−
sin
(
−
θ
)
sin
(
−
θ
)
cos
(
−
θ
)
]
=
[
cos
θ
sin
θ
−
sin
θ
cos
θ
]
\mathbf{R}_{-\theta} = \begin{bmatrix} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta) & \cos(-\theta) \end{bmatrix} = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix}
R−θ=[cos(−θ)sin(−θ)−sin(−θ)cos(−θ)]=[cosθ−sinθsinθcosθ]
其转置矩阵为:
R
θ
T
=
[
cos
θ
sin
θ
−
sin
θ
cos
θ
]
\mathbf{R}_\theta^T = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix}
RθT=[cosθ−sinθsinθcosθ]
可见 R − θ = R θ T \mathbf{R}_{-\theta} = \mathbf{R}_\theta^T R−θ=RθT,即 R θ T = R θ − 1 \mathbf{R}_\theta^T = \mathbf{R}_\theta^{-1} RθT=Rθ−1,满足正交矩阵(Orthogonal Matrix)定义。
齐次坐标系下旋转矩阵的正交性
2D 旋转变换的齐次矩阵形式为:
R = [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] \mathbf{R} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} R= cosθsinθ0−sinθcosθ0001
其转置矩阵为:
R
T
=
[
cos
θ
sin
θ
0
−
sin
θ
cos
θ
0
0
0
1
]
=
R
−
θ
\mathbf{R}^T = \begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} = \mathbf{R}_{-\theta}
RT=
cosθ−sinθ0sinθcosθ0001
=R−θ
同样满足正交矩阵定义,由此可推广:3D 坐标系(含笛卡尔坐标与齐次坐标)下的旋转矩阵(Rotation Matrix)均为正交矩阵。
3D 齐次坐标旋转矩阵
3D 空间中绕不同坐标轴的旋转矩阵如下(齐次坐标形式,4×4 矩阵):
1. 绕 x 轴旋转矩阵 R x ( α ) \mathbf{R}_x(\alpha) Rx(α)
R x ( α ) = ( 1 0 0 0 0 cos α − sin α 0 0 sin α cos α 0 0 0 0 1 ) \mathbf{R}_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} Rx(α)= 10000cosαsinα00−sinαcosα00001
- 旋转轴:x 轴(水平向右方向)。
- 旋转规则:右手拇指指向 x 轴正方向,四指弯曲方向为旋转正方向(角度 α \alpha α)。
- 坐标变化:仅 y、z 坐标随 cos α / sin α \cos\alpha/\sin\alpha cosα/sinα变换,x 坐标保持不变。
2. 绕 y 轴旋转矩阵 R y ( α ) \mathbf{R}_y(\alpha) Ry(α)
R y ( α ) = ( cos α 0 sin α 0 0 1 0 0 − sin α 0 cos α 0 0 0 0 1 ) \mathbf{R}_y(\alpha) = \begin{pmatrix} \cos\alpha & 0 & \sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\alpha & 0 & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} Ry(α)= cosα0−sinα00100sinα0cosα00001
- 旋转轴:y 轴(竖直向上方向)。
- 旋转规则:右手拇指指向 y 轴正方向,四指弯曲方向为旋转正方向(角度 α \alpha α)。
- 坐标变化:仅 x、z 坐标随 cos α / sin α \cos\alpha/\sin\alpha cosα/sinα变换,y 坐标保持不变。
3. 绕 z 轴旋转矩阵 R z ( α ) \mathbf{R}_z(\alpha) Rz(α)
R z ( α ) = ( cos α − sin α 0 0 sin α cos α 0 0 0 0 1 0 0 0 0 1 ) \mathbf{R}_z(\alpha) = \begin{pmatrix} \cos\alpha & -\sin\alpha & 0 & 0 \\ \sin\alpha & \cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} Rz(α)= cosαsinα00−sinαcosα0000100001
- 旋转轴:z 轴(垂直于 xy 平面向外的方向)。
- 旋转规则:右手拇指指向 z 轴正方向,四指弯曲方向为旋转正方向(角度 α \alpha α)。
- 坐标变化:仅 x、y 坐标随 cos α / sin α \cos\alpha/\sin\alpha cosα/sinα变换,z 坐标保持不变。
需注意:
-
绕 y y y 轴的旋转矩阵与绕 x x x 轴、 z z z 轴的旋转矩阵存在符号差异。这是因为 x x x 轴单位向量与 z z z 轴单位向量的叉乘结果为 y y y 轴负向向量,导致旋转角度等效为原值的负值,进而引发矩阵元素符号的变化。
-
所有仿射变换均可表示为“线性变换后接平移”的组合(即线性变换先作用于点,再进行平移)。
-
在齐次坐标表示下,该过程可等价为对扩展后的向量左乘单个齐次变换矩阵(二维仿射变换对应 3×3 矩阵,三维仿射变换对应 4×4 矩阵)。
-
若涉及多个基本仿射变换(如旋转、缩放、平移的组合),其对应的齐次矩阵可通过矩阵乘法按变换执行的逆序合并为一个整体,最终通过单次左乘完成完整变换。
- 仿射变换 | 原理、矩阵构造(篇 2)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/155754868 - 仿射变换 | 原理、矩阵构造(篇 3)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/155774996
via:
-
空间直角坐标转换之仿射变换 - 3echo - 博客园
https://www.cnblogs.com/3echo/archive/2008/06/01/1211641.html -
仿射变换(Affine Transformation)在2D和3D坐标下的变换矩阵和性质及齐次坐标系(Homogeneous Coordinates)的应用 - 知乎
https://zhuanlan.zhihu.com/p/465490024- GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1X7411F744/ - GAMES101: 现代计算机图形学入门
https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
- GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibili
 仿射变换原理与矩阵构造
仿射变换原理与矩阵构造





















 3035
3035

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








