仿射变换 | 原理、矩阵构造（篇 2）

注：本文为 “仿射变换” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

---

仿射变换（Affine Transformation）原理及应用

Godswisdom 于 2019-08-09 17:35:59 发布

1 仿射变换的定义与几何不变性

1.1 定义

仿射变换（Affine Transformation）是线性变换与平移变换的复合运算，涵盖缩放（Scale）、平移（Translation）、旋转（Rotation）、反射（Reflection）、错切（Shear Mapping）等具体形式。其特征表现为：变换前后直线的线性特征保持不变，平行线仍为平行线。

1.2 几何不变性

仿射变换过程中，以下几何性质保持不变：

1. 凸性：变换前的凸集，变换后仍为凸集；
2. 共线性：若多个点在变换前共线，则变换后仍保持共线关系；
3. 平行性：若两条直线在变换前平行，则变换后仍保持平行关系；
4. 共线比例不变性：变换前同一直线上两条线段的长度比例，变换后保持不变。

2 仿射变换的数学表达形式

2.1 一般形式

设集合 $X$ 中的任意元素 $x$，其仿射变换可表示为：
$$f(x)=Ax+b,x\in X$$
其中，$A$ 为线性变换矩阵，$b$ 为平移向量。该形式清晰体现了仿射变换“线性变换+平移”的复合本质。

2.2 二维图像中的齐次坐标表示

在二维图像变换场景中，为将线性变换与平移变换统一为矩阵乘法形式（便于计算机并行计算与复合变换推导），需引入齐次坐标（将二维点 $(x,y)$ 扩展为三维向量 $(x,y,1)$）。此时仿射变换的矩阵表达式为：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}{R}_{00}& R_{01}& T_x\\ R_{10}& R_{11}& T_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

该矩阵可拆解为两部分：

• 线性变换模块：由 $2\times 2$ 矩阵 $\left[\begin{array}{cc}{R}_{00}& R_{01}\\ R_{10}& R_{11}\end{array}\right]$ 实现，负责缩放、旋转、反射、错切等操作；
• 平移变换模块：由向量 $(T_x,T_y)$ 实现，对应矩阵第三列的前两个元素，负责图形的位置偏移。

齐次坐标表示的优势在于：可通过矩阵乘法实现多个仿射变换的复合（如先旋转后平移），无需单独处理平移向量，简化了变换的串联计算。

3 仿射变换的具体形式与矩阵构造逻辑

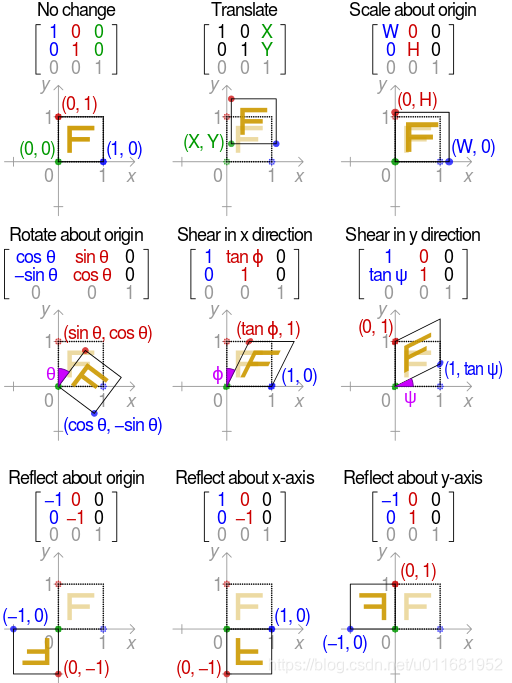
3.1 平移变换

平移变换仅改变图形的位置，不改变图形的形状、大小与方向。此时线性变换模块为单位矩阵（不改变原始坐标的线性关系），平移向量 $(T_x,T_y)$ 决定平移的方向与距离。其变换矩阵为：
$$M=\left[\begin{array}{ccc}1& 0& T_x\\ 0& 1& T_y\\ 0& 0& 1\end{array}\right]$$
其中，$T_x$ 为 $x$ 轴方向的平移量（正值向右，负值向左），$T_y$ 为 $y$ 轴方向的平移量（正值向下/向上，取决于坐标系定义）。

3.2 反射变换

反射变换（镜像变换）是图形关于某条直线的对称变换，其本质是改变坐标轴的符号方向。以常见的“关于 $x$ 轴反射”为例，变换后 $x$ 坐标保持不变，$y$ 坐标取反，其变换矩阵为：
$$M=\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ 0& 0& 1\end{array}\right]$$
若需实现关于 $y$ 轴反射，只需将矩阵中 $x$ 坐标对应的系数取反，即

$$\left[\begin{array}{ccc}-1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

3.3 旋转变换

旋转变换的关键是确定旋转矩阵中 $\sin \theta$ 的符号，该符号由坐标原点位置和旋转方向共同决定。以下分两种典型坐标系场景推导矩阵构造逻辑：

3.3.1 坐标系 1：原点为左下角（数学标准坐标系）

该坐标系中，$x$ 轴向右，$y$ 轴向上，符合数学中的平面直角坐标系定义。

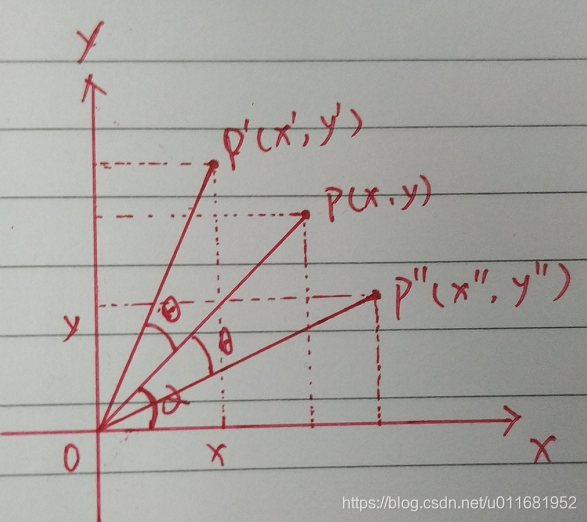
设点 $P(x,y)$ 到原点的距离为 1（单位向量），与 $x$ 轴夹角为 $\alpha$，则其坐标可由三角函数表示为：
$$\{\begin{array}{l}x=\cos \alpha \\ y=\sin \alpha \end{array}$$

• 逆时针旋转 $\theta$ 角：
  根据三角函数和角公式 $\cos (\alpha +\theta )=\cos \alpha \cos \theta -\sin \alpha \sin \theta$、$\sin (\alpha +\theta )=\sin \alpha \cos \theta +\cos \alpha \sin \theta$，旋转后点 $P^{\prime }(x^{\prime },y^{\prime })$ 的坐标为：
  $$\{\begin{array}{l}{x}^{\prime }=x\cos \theta -y\sin \theta \\ y^{\prime }=x\sin \theta +y\cos \theta \end{array}$$
  对应的旋转矩阵（线性变换模块）为：
  $$R^{\prime }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$

• 顺时针旋转 $\theta$ 角：
  同理，利用差角公式 $\cos (\alpha -\theta )=\cos \alpha \cos \theta +\sin \alpha \sin \theta$、$\sin (\alpha -\theta )=\sin \alpha \cos \theta -\cos \alpha \sin \theta$，旋转后点 $P^{\prime \prime }(x^{\prime \prime },y^{\prime \prime })$ 的坐标为：
  $$\{\begin{array}{l}{x}^{\prime \prime }=x\cos \theta +y\sin \theta \\ y^{\prime \prime }=-x\sin \theta +y\cos \theta \end{array}$$
  对应的旋转矩阵为：
  $$R^{\prime \prime }=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]$$

3.3.2 坐标系 2：原点为左上角（图像坐标系，如 OpenCV）

图像处理中，坐标系通常定义为：原点在图像左上角，$x$ 轴向右，$y$ 轴向下。

该坐标系的 $y$ 轴方向与数学标准坐标系相反，导致旋转矩阵的符号规则发生变化：

• 逆时针旋转 $\theta$ 角：
  由于 $y$ 轴方向反转，逆时针旋转的效果等价于数学标准坐标系中顺时针旋转 $\theta$ 角，旋转矩阵为：
  $$R^{\prime }=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]$$

• 顺时针旋转 $\theta$ 角：
  同理，其效果等价于数学标准坐标系中逆时针旋转 $\theta$ 角，旋转矩阵为：
  $$R^{\prime \prime }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$

3.3.3 旋转变换矩阵总结

旋转矩阵中 $\sin \theta$ 的符号由“坐标原点位置”和“旋转方向”共同决定，规律如下：

坐标系类型	逆时针旋转 $\theta$ 角的矩阵	顺时针旋转 $\theta$ 角的矩阵
原点在左下角	$\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$	$\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]$
原点在左上角（OpenCV）	$\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]$	$\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$

3.4 错切变换（补充）

错切变换是一种线性变换，其特点是图形的一边保持固定，另一边沿某一方向产生偏移，导致图形发生“剪切”变形。常见的错切变换分为 $x$ 轴方向错切和 $y$ 轴方向错切：

• $x$ 轴方向错切（$y$ 坐标影响 $x$ 坐标）：
  $$M=\left[\begin{array}{ccc}1& k& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
  其中，$k$ 为错切系数，$k>0$ 时向右错切，$k<0$ 时向左错切。

• $y$ 轴方向错切（$x$ 坐标影响 $y$ 坐标）：
  $$M=\left[\begin{array}{ccc}1& 0& 0\\ k& 1& 0\\ 0& 0& 1\end{array}\right]$$
  其中，$k$ 为错切系数，$k>0$ 时向下错切，$k<0$ 时向上错切。

4 OpenCV 中的仿射变换实现

OpenCV 作为计算机视觉领域的开源库，提供了成熟的仿射变换接口，其中 getRotationMatrix2D 函数是生成旋转+缩放+平移复合变换矩阵的重要工具。

4.1 函数原型与参数说明

CV_EXPORTS_W Mat getRotationMatrix2D( Point2f center, double angle, double scale );

• 参数详解：
  1. center：源图像的旋转中心（二维坐标点 $(center.x,center.y)$），用于指定旋转操作的基准点；
  2. angle：旋转角度（单位为度），遵循 OpenCV 坐标系规则（原点在左上角），正值表示逆时针旋转；
  3. scale：图像的各向同比缩放因子（$scale>1$ 时放大，$0<scale<1$ 时缩小）。

4.2 生成的仿射矩阵形式

函数输出为 $2\times 3$ 矩阵（省略齐次坐标的第三行 $[0,0,1]$，符合 OpenCV 中 warpAffine 函数的输入要求），形式如下：
$$\left[\begin{array}{ccc}\alpha & \beta & (1-\alpha )\cdot center.x-\beta \cdot center.y\\ -\beta & \alpha & \beta \cdot center.x+(1-\alpha )\cdot center.y\end{array}\right]$$
其中，$\alpha =scale\cdot \cos \theta$，$\beta =scale\cdot \sin \theta$（$\theta$ 为 angle 转换后的弧度值，即 $\theta =angle\times \frac{\pi }{180}$）。

4.3 矩阵构造的底层逻辑

该矩阵的构造过程是三次变换的复合（按“先平移→再缩放旋转→最后逆平移”的顺序），具体推导如下：

1. 第一步：平移变换——将旋转中心移至坐标原点
   为使旋转围绕指定中心进行，需先将该中心平移至原点，变换矩阵为：
   $$T_1=\left[\begin{array}{ccc}1& 0& -center.x\\ 0& 1& -center.y\\ 0& 0& 1\end{array}\right]$$

2. 第二步：缩放与旋转变换——复合操作
   先按 scale 因子缩放图像，再按 angle 旋转图像，两者的复合矩阵（齐次坐标形式）为：
   $$S\cdot R=\left[\begin{array}{ccc}scale& 0& 0\\ 0& scale& 0\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{ccc}\cos \theta & \sin \theta & \\ -\sin \theta & \cos \theta & \\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}\alpha & \beta & 0\\ -\beta & \alpha & 0\\ 0& 0& 1\end{array}\right]$$
   其中，$\alpha =scale\cdot \cos \theta$，$\beta =scale\cdot \sin \theta$，体现了缩放与旋转的耦合关系。

3. 第三步：逆平移变换——将旋转中心移回原位置
   缩放旋转完成后，需将原点处的旋转中心移回原始坐标，变换矩阵为：
   $$T_2=\left[\begin{array}{ccc}1& 0& center.x\\ 0& 1& center.y\\ 0& 0& 1\end{array}\right]$$

4. 复合变换矩阵推导
   三次变换的复合顺序为 $T_2\cdot (S\cdot R)\cdot T_1$，展开计算如下：
   $$\begin{array}{rl}{T}_2\cdot (S\cdot R)\cdot T_1& =\left[\begin{array}{ccc}1& 0& center.x\\ 0& 1& center.y\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{ccc}\alpha & \beta & 0\\ -\beta & \alpha & 0\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{ccc}1& 0& -center.x\\ 0& 1& -center.y\\ 0& 0& 1\end{array}\right]\\ & =\left[\begin{array}{ccc}\alpha & \beta & (1-\alpha )\cdot center.x-\beta \cdot center.y\\ -\beta & \alpha & \beta \cdot center.x+(1-\alpha )\cdot center.y\\ 0& 0& 1\end{array}\right]\end{array}$$
   省略第三行后，即得到 getRotationMatrix2D 函数输出的 $2\times 3$ 矩阵。

4.4 函数源码解析

以下为 getRotationMatrix2D 函数的实现代码（基于 OpenCV 源码简化），与上述推导逻辑完全一致：

cv::Mat cv::getRotationMatrix2D( Point2f center, double angle, double scale )
{
    CV_INSTRUMENT_REGION();  // 性能监控标记
    angle *= CV_PI / 180;    // 角度转换为弧度
    double alpha = std::cos(angle) * scale;  // 缩放+旋转的x方向系数
    double beta = std::sin(angle) * scale;   // 缩放+旋转的y方向系数
    Mat M(2, 3, CV_64F);     // 创建2×3的64位浮点型矩阵
    double* m = M.ptr<double>();  // 获取矩阵数据指针
    m[0] = alpha;
    m[1] = beta;
    // 平移分量计算：对应矩阵第三列第一行
    m[2] = (1 - alpha) * center.x - beta * center.y;
    m[3] = -beta;
    m[4] = alpha;
    // 平移分量计算：对应矩阵第三列第二行
    m[5] = beta * center.x + (1 - alpha) * center.y;
    return M;
}

5 参考文献

[1] 仿射变换详解 warpAffine
https://www.cnblogs.com/dupuleng/articles/4055020.html
[2] 仿射变换（Affine Transformation）
https://blog.youkuaiyun.com/robert_chen1988/article/details/80498805
[3] OpenCV 学习（三十五）之仿射变换 warpAffine.
https://blog.youkuaiyun.com/keith_bb/article/details/56331356
[4] OpenCV 官方文档. getRotationMatrix2D
https://docs.opencv.org/

---

图像坐标空间变换：仿射变换（Affine Transformation）

拜阳 原创于 2020-05-04 19:32:44 发布

仿射变换（Affine Transformation）简介

仿射变换的定义为：对一个向量空间依次执行一次线性变换（linear transformation）和一次平移（translation），将其映射至另一个向量空间的操作。
仿射变换对点、线、面具有特定的不变性，具体表现为：

• 变换后，点仍为点，线仍为线，面仍为面（若为 3D 投影变换，在特定视角下，面可能退化为线，线可能退化为点）；
• 变换后，平行线与平行面的平行性保持不变；
• 变换后，图形间的部分比例关系维持恒定，例如两条平行线的长度比、点在线段中的位置比例均不发生改变。

注意：仿射变换无法保证角度的不变性。

仿射变换的基础类型

仿射变换的基础形式包含恒等（identity）、尺度（scaling）、旋转（rotation）、剪切（shear）、镜像（reflection）与平移（translation）。其中，除平移外，其余类型均属于线性变换。线性变换通过矩阵乘法实现，平移则通过向量加法实现。
上述基础变换类型的划分依据为变换效果，从数学角度而言并非严格互斥，存在包含关系，例如恒等变换可视为宽高方向缩放倍数均为 1 的尺度变换。该分类方式无需过度深究，因其更贴合图像领域的常规认知习惯。

下文将采用线性方程组与矩阵两种形式，对各类变换进行数学描述。
首先进行符号约定：使用 $(u,v)$ 表示原始图像中的坐标，使用 $(x,y)$ 表示变换后图像的坐标。
在矩阵乘法表达式中，坐标以行向量形式置于左侧，变换矩阵置于右侧。此形式的优势在于，使用 numpy、tensorflow 等具备向量化矩阵乘法算子的工具时，无需对坐标矩阵调整通道维度并执行 reshape 操作。若不关注代码实现的便利性，将变换矩阵置于左侧、坐标以列向量形式置于右侧亦可行，部分教科书也采用该形式。

恒等

线性方程组形式：
$$\{\begin{array}{l}x=u\\ y=v\end{array}$$
矩阵形式：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

尺度

线性方程组形式：
$$\{\begin{array}{l}x=\alpha u\\ y=\beta v\end{array}$$
矩阵形式：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}\alpha & 0\\ 0& \beta \end{array}\right]$$

旋转

线性方程组形式：
$$\{\begin{array}{l}x=\cos (\theta )u-\sin (\theta )v\\ y=\sin (\theta )u+\cos (\theta )v\end{array}$$
矩阵形式：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}\cos (\theta )& \sin (\theta )\\ -\sin (\theta )& \cos (\theta )\end{array}\right]$$

剪切

剪切变换分为水平剪切与垂直剪切，分别表述如下：

水平剪切

线性方程组形式：
$$\{\begin{array}{l}x=u+s_{v}v\\ y=v\end{array}$$
矩阵形式：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}1& 0\\ s_v& 1\end{array}\right]$$

垂直剪切

线性方程组形式：
$$\{\begin{array}{l}x=u\\ y=s_{u}u+v\end{array}$$
矩阵形式：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}1& s_u\\ 0& 1\end{array}\right]$$

镜像

线性方程组形式：
$$\{\begin{array}{l}x=-u\\ y=v\end{array}$$
矩阵形式：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$$

平移

线性方程组形式：
$$\{\begin{array}{l}x=u+t_x\\ y=v+t_y\end{array}$$
矩阵形式：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]+\left[\begin{array}{cc}{t}_x& t_y\end{array}\right]$$

多个线性变换矩阵相乘可实现基础线性变换的叠加，例如同时实现旋转与尺度变换的表达式为：
$$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}\alpha & 0\\ 0& \beta \end{array}\right]\left[\begin{array}{cc}\cos (\theta )& \sin (\theta )\\ -\sin (\theta )& \cos (\theta )\end{array}\right]$$
实际计算时，通常先将两个 $2\times 2$ 矩阵相乘，再与左侧坐标向量运算，仅需一次坐标变换即可完成复合变换。（上述公式仅展示单个点的坐标变换，实际应用中需对图像中 $height\times width$ 个像素点执行坐标变换，该计算方式可显著降低运算量。）

仿射变换通式

各类基础变换可整合为仿射变换通式，其线性方程组形式为：
$$\{\begin{array}{l}x=t_{11}u+t_{21}v+t_{31}\\ y=t_{12}u+t_{22}v+t_{32}\end{array}$$
该通式可通过三种方式表示为矩阵形式：

1. 分离线性变换与平移的形式：
   此形式符合仿射变换的基础定义，但实际应用中较少采用，因需执行两次矩阵运算（一次乘法、一次加法），运算流程不够简洁。
   $$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}{t}_{11}& t_{12}\\ t_{21}& t_{22}\end{array}\right]+\left[\begin{array}{cc}{t}_{31}& t_{32}\end{array}\right]$$

2. 融合线性变换与平移的形式：
   该形式由线性方程组直接推导而来，仅需一次矩阵乘法即可完成线性变换与平移操作，是实际应用中最常用的形式。
   $$\left[\begin{array}{cc}x& y\end{array}\right]=\left[\begin{array}{ccc}u& v& 1\end{array}\right]\left[\begin{array}{cc}{t}_{11}& t_{12}\\ t_{21}& t_{22}\\ t_{31}& t_{32}\end{array}\right]$$
   将等号右侧第一个矩阵写为 $\left[\begin{array}{ccc}u& v& 1\end{array}\right]$ 的形式，该坐标形式称为齐次坐标，具有重要的理论与应用价值。在 2D 图像仿射变换中，齐次坐标最直观的作用是将仿射变换通式整合为单次矩阵乘法，实现线性变换与平移的合并；而在透视变换（Projective Transformation）的推导中，齐次坐标是必需的数学工具，同时也是计算机图形学的基础之一。本文暂不展开讨论透视变换与图形学相关内容。

3. 全齐次坐标形式：
   该形式是第二种形式的延伸，将等号左侧也表示为齐次坐标，是教科书中最常见的形式。但在仿射变换场景下，变换矩阵的第三列固定为 ${\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$，无实际意义且存在少量计算冗余，因此更推荐第二种形式。
   $$\left[\begin{array}{ccc}x& y& 1\end{array}\right]=\left[\begin{array}{ccc}u& v& 1\end{array}\right]\left[\begin{array}{ccc}{t}_{11}& t_{12}& 0\\ t_{21}& t_{22}& 0\\ t_{31}& t_{32}& 1\end{array}\right]$$

示例：人脸位置对齐

本节以人脸识别中的人脸位置对齐为例，说明仿射变换矩阵的求解方法及应用场景，以下为相关背景知识说明。

人脸识别是 2020 年深度学习领域最成功的应用方向之一。相较于行人重识别、ImageNet 通用分类等任务，在同等规模训练集（1000 万样本）与测试集（100 万样本）、测试集准确率达 95% 为合格标准的条件下，人脸识别更易达到合格要求，因此该任务本身的难度相对较低。其挑战在于极高的精度要求：95% 的准确率无法满足实际应用需求，例如人脸识别支付场景中，若每 100 笔订单存在 5 笔识别错误，将引发严重的安全问题。人脸识别的准确率需达到 99.999…%（小数点后多位 9），2019 年相关技术文档提出的指标为：在特定拒识率下，误识率不高于千万分之一（即对难以识别的人脸图像可拒绝识别，一旦确认识别则必须保证准确性）。

在高精度要求下，人脸识别的数据预处理流程与其他图像识别任务存在差异，人脸位置对齐是关键环节之一，可有效降低因位置偏差导致的误识别率。

具体流程为：完成人脸检测后，执行人脸特征点回归（通常 5 个特征点即可满足需求：双眼中心、鼻尖、双侧嘴角）。将回归得到的 5 个特征点坐标（记为 $(u,v)$）配准至预定义的五点模板坐标（记为 $(x,y)$）。由于特征点与模板坐标均为已知量，仿射变换通式中仅变换矩阵为未知量，可通过最小二乘法反推变换矩阵；再利用该矩阵对原始人脸图像执行坐标变换，完成位置对齐。

需补充说明的是，并非所有图像识别任务均可执行位置对齐。人脸识别能够实施该操作的前提是：人脸图像具有固定的结构模式，眉毛、眼睛、鼻子、嘴巴的相对位置不会发生显著偏移（例如眼睛不会出现在鼻子与嘴巴之间）。

注意事项：图像索引与坐标的对应关系

理论推导阶段通常无需引入图像索引（即常用的 $(i,j)$），但代码实现时必须使用，此时需特别注意图像索引与坐标的映射关系。图像索引中，$i$ 表示行索引，$j$ 表示列索引，对应关系如下：

$i\to 行\to y$
$j\to 列\to x$

因此，像素索引为 $(i,j)$ 的点对应的坐标为 $(y,x)$。若该对应关系错误，可能导致非预期的变换结果（例如顺时针旋转操作实际执行后为逆时针旋转）。

数据准备

以下通过 OpenCV 编写简易交互程序，用于获取图像中指定像素的坐标：

import cv2

WIN_NAME = 'pick_points'
IMAGE_FILE = 'test.png'

def pick_points(event, x, y, flags, param):
    if event == cv2.EVENT_LBUTTONDOWN:
        print('x = %d, y = %d' % (x, y))

cv2.namedWindow(WIN_NAME, 0)
cv2.setMouseCallback(WIN_NAME, pick_points)
image = cv2.imread(IMAGE_FILE, cv2.IMREAD_UNCHANGED)
while True:
    cv2.imshow(WIN_NAME, image)
    key = cv2.waitKey(30)
    if key == 27:  # ESC
        break
cv2.destroyAllWindows()

使用时需修改程序中图像文件的路径，路径中避免包含中文字符。运行程序后，左键点击图像即可通过 print 函数输出鼠标位置的坐标。

本示例原计划使用人脸图像，但为避免肖像权问题，改用大猩猩面部图像。该图像本地分辨率为 550 × 333（宽 × 高），若上传后分辨率变化，可通过上述程序重新拾取坐标。

坐标拾取顺序为：左眼、右眼、鼻尖、左嘴角、右嘴角（左右以观察者视角为准，无需考虑拍摄时的镜像变换）。拾取的原始图像坐标（$(u,v)$）如下：

$u_1=288,v_1=115$
$u_2=334,v_2=119$
$u_3=278,v_3=160$
$u_4=250,v_4=193$
$u_5=318,v_5=192$

人脸对齐需使用预定义的五点模板，本示例针对大猩猩面部构造了一个尺寸为 100 × 100 的五点模板，坐标（$(x,y)$）如下：

$x_1=31.3,y_1=45.2$
$x_2=67.8,y_2=45.2$
$x_3=49.5,y_3=68.7$
$x_4=35.2,y_4=84.8$
$x_5=62.6,y_5=84.8$

该模板为模拟数据，无实际标注依据。

求解仿射变换矩阵

前向映射

将 5 组对应点代入仿射变换通式，可得：
$$\{\begin{array}{l}{x}_1=t_{11}{u}_1+t_{21}{v}_1+t_{31}1\\ y_1=t_{12}{u}_1+t_{22}{v}_1+t_{32}1\\ x_2=t_{11}{u}_2+t_{21}{v}_2+t_{31}1\\ y_2=t_{12}{u}_2+t_{22}{v}_2+t_{32}1\\ ⋮\\ x_5=t_{11}{u}_5+t_{21}{v}_5+t_{31}1\\ y_5=t_{12}{u}_5+t_{22}{v}_5+t_{32}1\end{array}$$
式中，$u,v,x,y$ 为已知量，$t_{ij}$ 为待求量。注意到 $t_{11},t_{21},t_{31}$ 仅与 $x$ 相关，$t_{12},t_{22},t_{32}$ 仅与 $y$ 相关，因此可将上述方程组拆分为两组：

第一组（与 $x$ 相关）：
$$\{\begin{array}{l}{x}_1=t_{11}{u}_1+t_{21}{v}_1+t_{31}1\\ x_2=t_{11}{u}_2+t_{21}{v}_2+t_{31}1\\ ⋮\\ x_5=t_{11}{u}_5+t_{21}{v}_5+t_{31}1\end{array}$$

第二组（与 $y$ 相关）：
$$\{\begin{array}{l}{y}_1=t_{12}{u}_1+t_{22}{v}_1+t_{32}1\\ y_2=t_{12}{u}_2+t_{22}{v}_2+t_{32}1\\ ⋮\\ y_5=t_{12}{u}_5+t_{22}{v}_5+t_{32}1\end{array}$$

定义如下矩阵与向量：
$$\begin{gathered} T_1=[t_{11},t_{21},t_{31}{]}^T,T_2=[t_{12},t_{22},t_{32}{]}^T \\ X=[x_1,x_2,\dots ,x_5{]}^T,Y=[y_1,y_2,\dots ,y_5{]}^T \end{gathered}$$
$$A=\left[\begin{array}{ccc}{u}_1& v_1& 1\\ u_2& v_2& 1\\ ⋮& ⋮& ⋮\\ u_5& v_5& 1\end{array}\right]$$

则两组方程组可简化为：$A{T}_1=X$，$A{T}_2=Y$。已知 $A,X,Y$，求解 $T_1,T_2$ 即可。该方程组为超定方程组（方程数多于未知量数），无精确解，需通过最小二乘法求解。

以 $A{T}_1=X$ 为例，最小二乘解的推导过程如下：
$$\begin{gathered} A{T}_1=X \\ {A}^{T}A{T}_1=A^{T}X \\ (A^{T}A{)}^{-1}{A}^{T}A{T}_1=(A^{T}A{)}^{-1}{A}^{T}X \\ {T}_1=(A^{T}A{)}^{-1}{A}^{T}X \end{gathered}$$

推导说明：

• 等式两侧左乘 $A^T$，将系数矩阵转换为正定方阵；
• 等式两侧左乘 $(A^{T}A{)}^{-1}$，左侧系数矩阵变为单位阵，右侧即为 $T_1$ 的解。

同理可得：$T_2=(A^{T}A{)}^{-1}{A}^{T}Y$。

前向映射的定义为：从原始图像坐标 $(u,v)$（整数）出发，经矩阵变换得到变换后坐标 $(x,y)$（通常为浮点数）。该方法易于理解，但实际计算中极少使用，原因是变换后的浮点坐标需通过插值获取像素值，而前向映射的计算结果对插值操作不友好，后向映射则更适配插值流程。

后向映射

后向映射的定义为：从变换后图像坐标 $(x,y)$（整数）出发，经矩阵变换得到其在原始图像中的对应坐标 $(u,v)$（通常为浮点数）。

后向映射的推导流程与前向映射类似，仅需交换 $(x,y)$ 与 $(u,v)$ 的位置，具体如下：

将 5 组对应点代入仿射变换通式：
$$\{\begin{array}{l}u=t_{11}x+t_{21}y+t_{31}\\ v=t_{12}x+t_{22}y+t_{32}\end{array}$$

展开可得：
$$\begin{gathered} \{\begin{array}{l}{u}_1=t_{11}{x}_1+t_{21}{y}_1+t_{31}1\\ u_2=t_{11}{x}_2+t_{21}{y}_2+t_{31}1\\ ⋮\\ u_5=t_{11}{x}_5+t_{21}{y}_5+t_{31}1\end{array} \\ \{\begin{array}{l}{v}_1=t_{12}{x}_1+t_{22}{y}_1+t_{32}1\\ v_2=t_{12}{x}_2+t_{22}{y}_2+t_{32}1\\ ⋮\\ v_5=t_{12}{x}_5+t_{22}{y}_5+t_{32}1\end{array} \end{gathered}$$

定义如下矩阵与向量：
$$\begin{gathered} T_1=[t_{11},t_{21},t_{31}{]}^T,T_2=[t_{12},t_{22},t_{32}{]}^T \\ U=[u_1,u_2,\dots ,u_5{]}^T,V=[v_1,v_2,\dots ,v_5{]}^T \end{gathered}$$
$$A=\left[\begin{array}{ccc}{x}_1& y_1& 1\\ x_2& y_2& 1\\ ⋮& ⋮& ⋮\\ x_5& y_5& 1\end{array}\right]$$

则方程组的最小二乘解为：
$$\begin{gathered} T_1=(A^{T}A{)}^{-1}{A}^{T}U \\ {T}_2=(A^{T}A{)}^{-1}{A}^{T}V \end{gathered}$$

定义 $\bar{A}=(A^{T}A{)}^{-1}{A}^T$，预先计算 $\bar{A}$ 可减少重复运算，此时解可简化为：
$$\begin{gathered} T_1=\bar{A}U \\ {T}_2=\bar{A}V \end{gathered}$$

后向映射代码实现

需注意，本文重点为仿射变换原理介绍，坐标变换后需执行插值操作以生成变换后图像。工程中常用双线性插值，本文为简化实现，采用最邻近插值（插值函数为 nearest_sampler）。若需深入了解插值方法，可参考：图像插值：最邻近（nearest）与双线性（bilinear）

# -*- coding: utf-8 -*-

import cv2
import numpy as np

def nearest_sampler(image, coords):
    """
    Nearest Neighbour sampler
    
    Parameters
    ----------
    image: ndarray
        source image, whose shape is [height, width, channels]
    coords: ndarray
        coordinates to be interpolated, the length of last axis should be 2,
        meaning 2D coordinate
    
    Returns
    -------
    output: ndarray
        the interpolated image, same shape as coords except the last axis
    """
    height, width, channels = image.shape[0:3]
    output_shape = list(coords.shape)
    coords = np.reshape(coords, (-1, output_shape[-1]))
    output_shape[-1] = channels
    coords = np.round(coords).astype(np.int32)
    idx = (coords[:, 0] >= 0) & (coords[:, 0] < width) & \
          (coords[:, 1] >= 0) & (coords[:, 1] < height)
    output = np.zeros((coords.shape[0], channels), dtype=np.uint8)
    output[idx] = image[coords[idx, 1], coords[idx, 0], :]
    output = np.reshape(output, output_shape)
    return output

if __name__ == '__main__':
    # feature points
    uv = np.array([[288, 115],
                   [334, 119],
                   [278, 160],
                   [250, 193],
                   [318, 192]])
    # model points
    xy = np.array([[31.3, 45.2],
                   [67.8, 45.2],
                   [49.5, 68.7],
                   [35.2, 84.8],
                   [62.6, 84.8]])

    # compute transform matrix
    U = np.reshape(uv[:, 0], [uv.shape[0], 1])
    V = np.reshape(uv[:, 1], [uv.shape[0], 1])
    A = np.zeros((xy.shape[0], 3))
    A[:, 0:2] = xy
    A[:, 2] = 1
    A_bar = np.linalg.inv(A.T @ A) @ A.T
    T1 = A_bar @ U
    T2 = A_bar @ V
    T = np.concatenate((T1, T2), axis=1)

    # coordinates mapping
    height = 100
    width = 100
    coords = np.meshgrid(np.arange(0, width), np.arange(0, height))
    # shape = [height, width, 2] after transpose
    coords = np.array(coords).transpose([1, 2, 0])
    ones = np.ones([height, width, 1])
    # homogeneous coordinates
    coords = np.concatenate((coords, ones), axis=2)
    # transformed coordinates
    coords = coords @ T

    # sampler
    image = cv2.imread('2.jpg')
    img = nearest_sampler(image, coords)

    cv2.imshow('affine', img)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

大猩猩面部对齐结果如下：

该结果存在变形，源于两类基础变换：

1. 宽高方向的缩放尺度不一致；
2. 剪切变换的引入。

实际人脸对齐场景中，通常需避免此类变形，要求宽高方向缩放尺度一致且无剪切变换。因此需对仿射变换施加约束，下文介绍该类特殊仿射变换矩阵的求解方法。

特殊仿射变换及变换矩阵求解方法

本节针对上述变形问题，定义如下约束条件：

1. 宽高方向的缩放尺度相同；
2. 不引入剪切变换。

此外，人脸对齐场景中通常不引入镜像变换，因此实际涉及的基础变换类型仅包括：

• 旋转；
• 尺度（宽高缩放因子相同）；
• 平移。

以下直接推导后向映射的变换表达式：
$$\left[\begin{array}{cc}u& v\end{array}\right]=\left[\begin{array}{cc}x& y\end{array}\right]\left[\begin{array}{cc}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{cc}\cos (\theta )& \sin (\theta )\\ -\sin (\theta )& \cos (\theta )\end{array}\right]+\left[\begin{array}{cc}{t}_u& t_v\end{array}\right]$$

合并后可得：
$$\left[\begin{array}{cc}u& v\end{array}\right]=\left[\begin{array}{ccc}x& y& 1\end{array}\right]\left[\begin{array}{cc}s\ast \cos (\theta )& s\ast \sin (\theta )\\ -s\ast \sin (\theta )& s\ast \cos (\theta )\\ t_u& t_v\end{array}\right]$$

定义变量：
$$\begin{gathered} a=s\ast \cos (\theta ) \\ b=s\ast \sin (\theta ) \\ c=t_u \\ d=t_v \end{gathered}$$

则变换表达式简化为：
$$\left[\begin{array}{cc}u& v\end{array}\right]=\left[\begin{array}{ccc}x& y& 1\end{array}\right]\left[\begin{array}{cc}a& b\\ -b& a\\ c& d\end{array}\right]$$

变换矩阵求解

将 5 组对应点代入上述表达式（仅推导后向映射）：
$$\{\begin{array}{l}{u}_1=a\ast x_1-b\ast y_1+c\ast 1+d\ast 0\\ u_2=a\ast x_2-b\ast y_2+c\ast 1+d\ast 0\\ ⋮\\ u_5=a\ast x_5-b\ast y_5+c\ast 1+d\ast 0\\ v_1=a\ast y_1+b\ast x_1+c\ast 0+d\ast 1\\ v_2=a\ast y_2+b\ast x_2+c\ast 0+d\ast 1\\ ⋮\\ v_5=a\ast y_5+b\ast x_5+c\ast 0+d\ast 1\end{array}$$

由于变换矩阵的第一列与第二列存在变量耦合（共享 $a,b$），无法拆分方程组分别求解，需通过一次最小二乘运算求解 4 个参数 $a,b,c,d$。

定义如下矩阵与向量：
$$A=\left[\begin{array}{cccc}{x}_1& -y_1& 1& 0\\ x_2& -y_2& 1& 0\\ ⋮& ⋮& ⋮& ⋮\\ x_5& -y_5& 1& 0\\ y_1& x_1& 0& 1\\ y_2& x_2& 0& 1\\ ⋮& ⋮& ⋮& ⋮\\ y_5& x_5& 0& 1\end{array}\right]$$
$$B=[u_1,u_2,\dots ,u_5,v_1,v_2,\dots ,v_5{]}^T$$
$$\bar{T}=[a,b,c,d{]}^T$$

则最小二乘解为：
$$\bar{T}=(A^{T}A{)}^{-1}{A}^{T}B$$

求得 $\bar{T}$ 后，按对应关系重组即可得到变换矩阵。以下为代码实现（仅变换矩阵求解部分与前文不同，其余代码一致，仍使用大猩猩面部数据）：

# -*- coding: utf-8 -*-

import cv2
import numpy as np

def nearest_sampler(image, coords):
    """
    Nearest Neighbour sampler
    
    Parameters
    ----------
    image: ndarray
        source image, whose shape is [height, width, channels]
    coords: ndarray
        coordinates to be interpolated, the length of last axis should be 2,
        meaning 2D coordinate
    
    Returns
    -------
    output: ndarray
        the interpolated image, same shape as coords except the last axis
    """
    height, width, channels = image.shape[0:3]
    output_shape = list(coords.shape)
    coords = np.reshape(coords, (-1, output_shape[-1]))
    output_shape[-1] = channels
    coords = np.round(coords).astype(np.int32)
    idx = (coords[:, 0] >= 0) & (coords[:, 0] < width) & \
          (coords[:, 1] >= 0) & (coords[:, 1] < height)
    output = np.zeros((coords.shape[0], channels), dtype=np.uint8)
    output[idx] = image[coords[idx, 1], coords[idx, 0], :]
    output = np.reshape(output, output_shape)
    return output

if __name__ == '__main__':
    # feature points
    uv = np.array([[288, 115],
                   [334, 119],
                   [278, 160],
                   [250, 193],
                   [318, 192]])
    # model points
    xy = np.array([[31.3, 45.2],
                   [67.8, 45.2],
                   [49.5, 68.7],
                   [35.2, 84.8],
                   [62.6, 84.8]])

    # compute transform matrix
    num = xy.shape[0]
    A = np.zeros((2 * num, 4))
    A[0:num, 0] = xy[:, 0]
    A[0:num, 1] = -xy[:, 1]
    A[0:num, 2] = 1
    A[num:2 * num, 0] = xy[:, 1]
    A[num:2 * num, 1] = xy[:, 0]
    A[num:2 * num, 3] = 1
    B = np.reshape(uv.T, [2 * num, 1])
    T_bar = np.linalg.inv(A.T @ A) @ A.T @ B
    T = np.zeros((3, 2))
    T[0, 0] = T_bar[0]
    T[0, 1] = T_bar[1]
    T[1, 0] = -T_bar[1]
    T[1, 1] = T_bar[0]
    T[2, 0] = T_bar[2]
    T[2, 1] = T_bar[3]

    # coordinates mapping
    height = 100
    width = 100
    coords = np.meshgrid(np.arange(0, width), np.arange(0, height))
    # shape = [height, width, 2] after transpose
    coords = np.array(coords).transpose([1, 2, 0])
    ones = np.ones([height, width, 1])
    # homogeneous coordinates
    coords = np.concatenate((coords, ones), axis=2)
    # transformed coordinates
    coords = coords @ T

    # sampler
    image = cv2.imread('2.jpg')
    img = nearest_sampler(image, coords)

    cv2.imshow('affine', img)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

约束后的对齐结果如下：

为便于对比，附上无约束的变形结果：

此外，附上手动旋转并裁剪原始图像的结果（裁剪为手动操作，位置与程序结果存在差异，仅用于对比两类仿射变换的变形效果）：

变形的主要原因是大猩猩面部呈侧视角，若为正视角，即使使用无约束仿射变换，变形程度也会显著降低。

重要注意事项：前向映射与后向映射矩阵不互逆

部分开发者为贴合教科书的前向映射理论，先求解前向映射矩阵，再通过求逆得到后向映射矩阵，该方法存在错误——前向与后向映射矩阵通常不满足互逆关系。仅当求解的线性方程组为正定（仅使用 3 组线性无关的特征点）时，互逆关系才成立，而该场景在实际应用中并不常见。

以下通过代码验证该结论（需将 3×2 变换矩阵补充 ${\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$ 扩展为 3×3 矩阵，以验证矩阵逆）：

# -*- coding: utf-8 -*-

import numpy as np

# feature points
uv = np.array([[288, 115],
               [334, 119],
               [278, 160],
               [250, 193],
               [318, 192]])
# model points
xy = np.array([[31.3, 45.2],
               [67.8, 45.2],
               [49.5, 68.7],
               [35.2, 84.8],
               [62.6, 84.8]])

# compute backward transform matrix
U = np.reshape(uv[:, 0], [uv.shape[0], 1])
V = np.reshape(uv[:, 1], [uv.shape[0], 1])
A = np.zeros((xy.shape[0], 3))
A[:, 0:2] = xy
A[:, 2] = 1
A_bar = np.linalg.inv(A.T @ A) @ A.T
T1 = A_bar @ U
T2 = A_bar @ V
T = np.concatenate((T1, T2), axis=1)
T_backward = np.concatenate((T, np.array([[0], [0], [1]])), axis=1)

# compute forward transform matrix
X = np.reshape(xy[:, 0], [xy.shape[0], 1])
Y = np.reshape(xy[:, 1], [xy.shape[0], 1])
A = np.zeros((xy.shape[0], 3))
A[:, 0:2] = uv
A[:, 2] = 1
A_bar = np.linalg.inv(A.T @ A) @ A.T
T1 = A_bar @ X
T2 = A_bar @ Y
T_forward = np.concatenate((T1, T2, np.array([[0], [0], [1]])), axis=1)

# verification
T_forward_inv = np.linalg.inv(T_forward)
T_mul = T_forward @ T_backward

计算得到的关键矩阵如下：
$$\begin{gathered} T_{forward}=\left[\begin{array}{ccc}0.488518& -0.0123897& 0\\ 0.177793& 0.51996& 0\\ -121.849& -11.6322& 1\end{array}\right] \\ {T}_{backward}=\left[\begin{array}{ccc}1.69603& 0.0564699& 0\\ -0.68687& 1.90407& 0\\ 255.175& 27.8433& 1\end{array}\right] \\ {T}_{forward\_inv}=\left[\begin{array}{ccc}2.02941& 0.048357& 0\\ -0.69393& 1.90669& 0\\ 239.21& 28.0712& 1\end{array}\right] \\ {T}_{mul}=\left[\begin{array}{ccc}0.837049& 0.00399568& 0\\ -0.0556026& 1.00008& 0\\ 56.5053& -1.18607& 1\end{array}\right] \end{gathered}$$

可见，$T_{forward\_inv}$ 与 $T_{backward}$ 存在明显差异，且 $T_{forward}$ 与 $T_{backward}$ 的乘积 $T_{mul}$ 并非单位矩阵，因此二者不满足互逆关系。

---

• 仿射变换 | 原理、矩阵构造（篇 1）-优快云博客
  https://blog.youkuaiyun.com/u013669912/article/details/155749696
• 仿射变换 | 原理、矩阵构造（篇 3）-优快云博客
  https://blog.youkuaiyun.com/u013669912/article/details/155774996

---

via：

• 仿射变换（Affine Transformation）原理及应用-优快云博客
  https://blog.youkuaiyun.com/u011681952/article/details/98942207
• 图像坐标空间变换：仿射变换（Affine Transformation）_像空间坐标系与像空间辅助坐标系的转换代码-优快云博客
  https://blog.youkuaiyun.com/bby1987/article/details/105695509