数学概念的形成与发展：研究与教学的要素

注：英文引文，机翻未校。
如有内容异常，请看原文。

---

Formation and development of mathematical concepts: Elements for research and teaching

数学概念的形成与发展：研究与教学的要素

Armando Morales-Carballo 1* , Miguel Díaz Cárdenas 1 , Angie Damián Mojica 1
阿曼多·莫拉莱斯-卡瓦略¹*、米格尔·迪亚斯·卡德纳斯¹、安吉·达米安·莫希卡¹
1 Universidad Autónoma de Guerrero, Guerrero, MEXICO
¹墨西哥格雷罗州格雷罗自治大学
*Corresponding Author: armandomorales@uagro.mx
*通讯作者：armandomorales@uagro.mx
Citation: Morales-Carballo, A., Díaz Cárdenas, M., & Damián Mojica, A. (2024). Formation and development of mathematical concepts: Elements for research and teaching. International Electronic Journal of Mathematics Education, 19(1), em0762. https://doi.org/10.29333/iejme/14023
引文格式：莫拉莱斯-卡瓦略、迪亚斯·卡德纳斯、达米安·莫希卡（2024）。《数学概念的形成与发展：研究与教学的要素》，《国际数学教育电子期刊》，第 19 卷第 1 期，文章编号 em0762。https://doi.org/10.29333/iejme/14023

The provided text appears to be a structured abstract of an academic article, with sections for article information and a brief summary of the content. Below is a revised version of the text without the table format:

Article Information:
Received: 28 Jul. 2023
Accepted: 25 Nov. 2023

Abstract:
This article presents a theoretical-didactic perspective on the formation and development of concepts concerning mathematical objects as a result of research on didactic difficulties in dealing with concepts in school.
摘要：
本文基于对学校教学中数学概念处理难点的研究，从理论-教学视角阐述了数学对象相关概念的形成与发展。

Keywords: mathematical object, concept, generalization
关键词： 数学对象、概念、概括

Introduction

引言

From a theoretical-didactic perspective, important research (Arteaga et al., 2009; Hernández-Gómez et al., 2019; Ramos & López, 2015; Winicki-Landman, 2006) suggests that mathematical concepts are a special category that should be considered in mathematics teaching, as they constitute the fundamental basis with which mathematical thinking operates.
从理论-教学视角来看，多项重要研究（阿特加等人，2009；埃尔南德斯-戈麦斯等人，2019；拉莫斯与洛佩斯，2015；维尼奇-兰德曼，2006）表明，数学概念是数学教学中应重点关注的特殊范畴，因为它们是数学思维运作的基础。

Through their formation and development, the objective of establishing and representing the relation between mathematics and objects whose existence is independent of human consciousness (objective reality) is favored (Ballester, 1992).
通过数学概念的形成与发展，有助于实现建立并表征数学与客观存在（独立于人类意识的事物）之间联系的目标（巴列斯特，1992）。

These works agree that the study of mathematical concepts and their treatment in the school environment can lead to the following achievements:
这些研究一致认为，对数学概念的研究及其在学校教学中的处理可达成以下成果：

1. Understanding concepts and their definitions is fundamental to understanding mathematical relation.
   理解概念及其定义是理解数学关系的基础。

2. It provides the basis for applying what has been learned in a justified and creative manner.
   为合理且创造性地应用所学知识提供基础。

3. The formation and definition of concepts represent an essential point for logical-verbal training.
   概念的形成与定义是逻辑-语言训练的关键环节。

4. The possibility of transmitting important ideological notions in the elaboration of concepts and their definitions, which allow for the fixation of qualities in the personality of the learner.
   在概念及其定义的阐述过程中，能够传递重要的思想观念，进而有助于学习者形成稳定的个人品质。

In this regard, research studies reported by Angulo et al. (2020), Hernández-Gómez et al. (2019), and Locia et al. (2018) have highlighted the importance of treating mathematical concepts as an essential part of the teaching and learning of mathematics.
对此，安古洛等人（2020）、埃尔南德斯-戈麦斯等人（2019）以及洛西亚等人（2018）的研究均强调，将数学概念视为数学教与学的核心组成部分具有重要意义。

They generally agree that many of the problems related to understanding mathematics are rooted in the insufficient treatment of mathematical concepts and the lack of methodological preparation for their incorporation and development as teaching objects in the classroom.
他们普遍认为，许多数学理解相关的问题，根源在于对数学概念的处理不足，以及在将其作为课堂教学对象进行融入和发展方面缺乏方法性准备。

In the literature, research has also identified that both students and teachers at different educational levels have significant difficulties with mathematical concepts, which hinder their understanding and development of various mathematical contents.
文献研究还发现，不同教育阶段的学生和教师在数学概念方面均存在显著困难，这些困难阻碍了他们对各类数学内容的理解与掌握。

Among the essential difficulties are those related to the definition, identification, and application of concepts (Morales & Damián, 2021a, 2021b; Morales-Carballo et al., 2022).
其中核心困难包括与概念的定义、识别和应用相关的问题（莫拉莱斯与达米安，2021a，2021b；莫拉莱斯-卡瓦略等人，2022）。

These difficulties may be due to the lack of conditions for understanding concepts and their definitions in learning activities (Hernández-Gómez et al., 2019), teacher training, curriculum approaches, among others.
这些困难可能源于学习活动中缺乏理解概念及其定义的条件（埃尔南德斯-戈麦斯等人，2019）、教师培训不足、课程方案不合理等多种因素。

Based on the referenced research, we identify the relevance of studying mathematical concepts and their assimilation as a means to develop mathematical knowledge.
基于上述研究，我们认为研究数学概念及其内化过程对于发展数学知识具有重要意义。

However, this position is still in development and often differs from what happens in practical activity at different educational levels.
然而，这一观点仍在发展阶段，且与不同教育阶段的实际教学实践往往存在差异。

It is commonly observed that in these practices, definitions are repeated to students as they are stated in texts (Hernández-Gómez et al., 2019).
常见的现象是，在实际教学中，教师会按照教材原文向学生重复概念定义（埃尔南德斯-戈麦斯等人，2019）。

This practice is undoubtedly not sufficient for developing students’ comprehension of concepts and mathematics in general.
毫无疑问，这种做法不足以帮助学生理解概念，也无法促进其对数学整体的理解。

For example, in the study plans and programs, at least in Mexico, the content on mathematical concepts proposed for treatment in school is generally presented as finished knowledge and not as a process.
例如，至少在墨西哥的教学计划和课程大纲中，学校拟教授的数学概念内容通常被视为已成型的知识，而非一个动态的形成过程。

This means that the activity on concept reconstruction and definition processes is not promoted.
这意味着，概念重构与定义形成过程相关的教学活动并未得到推广。

The authors argue that this absence does not allow students in training and even the teacher to reflect on these processes of elaboration and development, which are essential, since they influence understanding.
作者认为，这种教学活动的缺失使得学生（甚至教师）无法对概念的阐述与发展过程进行反思——而这些过程至关重要，因为它们直接影响对概念的理解。

The aim of this work is to contribute important elements to research in mathematics education on the formation and assimilation of concepts and to provide insights into the highlighted issues.
本研究旨在为数学教育领域中与概念形成及内化相关的研究提供重要参考要素，并针对上述问题提出见解。

The objective is to develop and exemplify a theoretical-didactic perspective for the formation and development of mathematical concepts, and to demonstrate its application in the field of Euclidean geometry.
研究目标是构建并举例说明一种用于数学概念形成与发展的理论-教学视角，并在欧几里得几何领域中展示该视角的应用。

Theoretical & Methodological Foundation

理论与方法基础

In the literature, different theoretical models have been identified that, from different perspectives, have been oriented towards the study of understanding in mathematics, seeking to describe and propose alternatives to influence this problem.
文献中已存在多种理论模型，这些模型从不同视角出发，致力于研究数学理解问题，旨在描述该问题并提出解决思路。

In this direction, Sierpinska (1987) considers the possibility of understanding as the overcoming of cognitive obstacles, i.e., from this viewpoint it is assumed that overcoming an obstacle means that the student or the one who constructs his knowledge must overcome his convictions and analyze the beliefs about the situation (the obstacle) from an external viewpoint.
在这一领域，希耶平斯卡（1987）将理解视为对认知障碍的克服，即从该视角来看，克服障碍意味着学生或知识构建者必须摒弃自身固有认知，并从外部视角分析与该情境（障碍）相关的观念。

In this way, it will be possible to prepare the conditions for identifying the objects associated with the concept, the invariant properties and the step to the generalization of the scope of application of the concepts, then synthesize the relationships between properties, facts and objects that are fundamental processes in such orientation for overcoming an obstacle.
通过这种方式，能够为以下环节创造条件：识别与概念相关的对象、确定不变属性、推进概念应用范围的概括过程，进而综合属性、事实与对象之间的关系——这些都是该视角下克服认知障碍的核心过程。

Another theoretical model of understanding is the one presented by Vinner (1991), from this theory the understanding of concepts is acquired when the student constructs an image of the concept (the collection of mental images, representations and related properties attributed to a concept) and as the image of the concept is developed, apparently conflicting images can be identified in this process, overcoming these situations leads the process towards the formal definition.
另一种理解相关的理论模型由文纳（1991）提出。该理论认为，当学生构建出“概念意象”（即与某一概念相关的心理图像、表征及属性的集合）时，便实现了对概念的理解；随着概念意象的发展，过程中可能会出现明显矛盾的意象，而克服这些矛盾情境则会推动理解过程向正式概念定义迈进。
The construction of concept images occurs when new information is incorporated and faces the consolidation of this information within the cognitive structure already present in the student.
概念意象的构建过程，是新信息被纳入学生已有认知结构并与之融合的过程。

In this sense, Tall (1991) considers that the notions of assimilation and accommodation influence the incorporation of information in the process of concept image development, thus favoring the stages of generalization and abstraction.
在这一意义上，托尔（1991）认为，“同化”与“顺应”的概念会影响概念意象发展过程中的信息整合，进而促进概括与抽象阶段的推进。

As can be identified in previous lines, the theoretical models of reference do not contradict each other; through different paths they address common aspects that influence mathematical understanding.
如前文所述，上述参考理论模型之间并不矛盾，它们通过不同路径探讨了影响数学理解的共同方面。

In the present research it is argued that the contribution of the elements for the understanding provided by the theoretical models of reference are included and enriched in the theoretical-didactic perspective for the formation and development of mathematical concepts presented in this work, which is based on the principle of apprehending is knowing, in the theory of knowledge, theory of activity and is nourished by the authors’ own vision.
本研究认为，这些参考理论模型所提供的与理解相关的要素，被纳入并丰富了本文提出的“数学概念形成与发展的理论-教学视角”中。该视角以“领会即认知”为原则，植根于知识论、活动理论，并融入了作者自身的观点。

Theory of Knowledge

知识论

Based on the principle that apprehend¹ is knowing, it is logical to think that anyone who wants to apprehend mathematics must be able to carry out processes of constructing mathematical knowledge, and therefore, guidance is needed on how these processes occur.
基于“领会即认知”这一原则，合理的推论是：任何想要领会数学的人，都必须能够开展数学知识的构建过程，因此，需要明确这些过程的发生机制。

¹ To apprehend commonly implies a material retention, but in this document it is used to signify a retention in the abstract realm. Thus, in theprocess of knowledge construction, conceptual apprehension involves retaining the meaning-through the formation of a mental image-of theessential characteristics of the object of knowledge.
注 1：“领会”通常意味着对具体事物的掌握，但在本文中，它特指对抽象概念的理解。因此，在知识构建的过程中，概念性的领会涉及通过形成心理意象来保留知识对象的本质特征所蕴含的意义。

The materialist approach of the theory of knowledge (Guétmanova, 1989) establishes that the cognitive process follows a schema consisting of six categories: sensation, perception, notion, concept, judgment, and reasoning.
知识论的唯物主义视角（格特曼诺娃，1989）认为，认知过程遵循由六个范畴构成的框架：感觉、知觉、表象、概念、判断、推理。

The first three categories correspond to what is called sensory or material knowledge, that is, the different forms of thought originating from direct reflections of concrete reality–material–on the human consciousness.
前三个范畴属于“感性知识”或“具象知识”，即源于客观现实（物质）在人类意识中直接反映的不同思维形式。

The last three categories correspond to what is called abstract thought, which are the different forms of thought originating from indirect reflections of subjective reality–non-material– on the human consciousness.
后三个范畴属于“抽象思维”，即源于主观现实（非物质）在人类意识中间接反映的不同思维形式。

The researcher affirms that abstract thought, through its three essential forms: concept, judgment, and reasoning, is the means for constructing theoretical knowledge.
研究者认为，抽象思维通过其三种基本形式（概念、判断、推理），成为构建理论知识的工具。

We know the laws of the world, the essence of objects and phenomena, and their commonalities through abstract thinking, the most complex form of knowledge.
抽象思维是最复杂的认知形式，通过它，我们能够认识世界的规律、事物与现象的本质及其共性。

Abstract or rational thinking reflects the world and its processes in a more complete and profound way than sensory knowledge.
相较于感性知识，抽象思维（或理性思维）能更全面、更深刻地反映世界及其发展过程。

The transition from sensory knowledge to abstract thinking is a leap in the cognitive process, a leap from knowledge of facts to knowledge of laws (Guétmanova, 1989, p. 13).
从感性知识到抽象思维的转变，是认知过程中的一次飞跃——从对事实的认知跃迁至对规律的认知（格特曼诺娃，1989，第 13 页）。

According to this approach, knowledge starts with live observation, that is, the set of sensations and perceptions through which the environment is reflected in the human brain (Campistrous & Rizo, 2003).
根据这一视角，认知始于直接观察，即通过一系列感觉与知觉，将外部环境反映到人类大脑中（坎皮斯特罗斯与里索，2003）。

However, the type of knowledge generated at this stage is always of a material or empirical nature.
然而，这一阶段产生的知识始终具有具象性或经验性。

On the perceptions, processes of analysis, synthesis, abstraction, and generalization are carried out to give rise to the formation of concepts, judgments, evaluations, relations, among other important components of the content to be learned.
在知觉的基础上，通过分析、综合、抽象、概括等过程，形成概念、判断、评价、关系等待学内容的重要组成部分。

In this way, a deeper stage of knowledge is reached, one that manages to abstract the most internal or essential features of objects and the invariant relation between them; the most stable regularities in phenomena, and the most refined algorithms in processes.
通过这种方式，认知进入更深层次——能够抽象出事物最本质的内在特征、事物间的不变关系、现象中最稳定的规律，以及过程中最精准的算法。

This higher knowledge can be achieved through the action of abstract thinking in its three categories: concept, judgment, and reasoning, which make up the second stage in the elaboration of knowledge.
这种高层次的认知，可通过抽象思维的三种形式（概念、判断、推理）实现，它们共同构成了知识构建的第二阶段。

Once this knowledge has been developed, it is applied in practical activity, where the need to develop such knowledge was found.
一旦形成这种知识，便会应用于实际活动中——而这种知识的构建需求，正是源于实际活动。

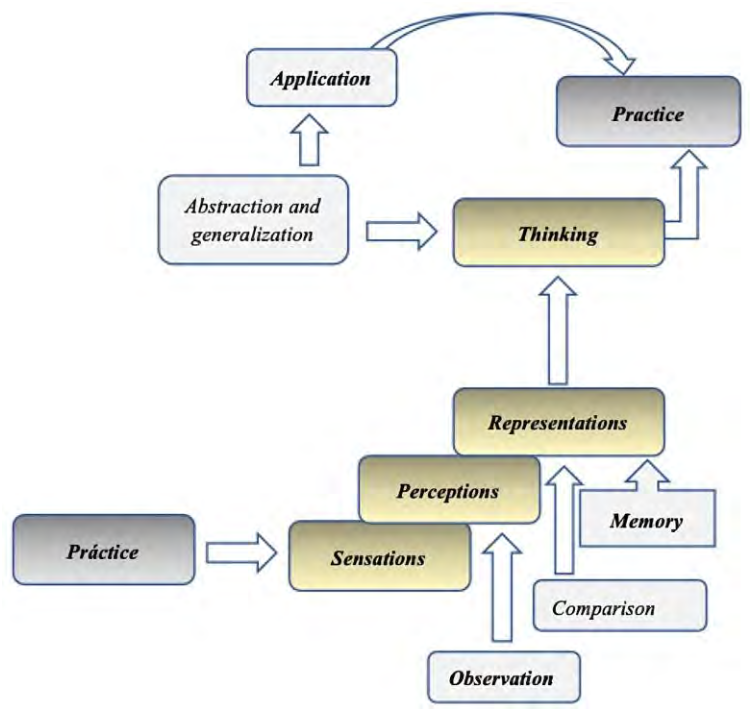
Figure 1. Representation of process of knowledge elaboration (Rizo & Campistrous, 2003)

In this regard, Rizo and Campistrous (2011) reinforce the justification that the path of knowledge begins with live perception (in practice) and culminates in practice, in qualitatively superior conditions after being enriched by a process of intellectual elaboration. Figure 1 shows an approach to the processes of thought that favor this dialectical path.
在这方面，里索和坎皮斯特罗斯（2011年）进一步佐证了这样的观点：知识的获取始于鲜活的感知（在实践中），并在经过智力加工过程的充实后，以更优的质态在实践中达到顶峰。图1展示了有助于这一辩证过程的思维流程。

Specifically speaking, the concept is the knowledge built on objects, phenomena or processes of reality; the judgment is a logical proposition whose content is concepts or relation between concepts, that is to say, its content is knowledge; finally, the reasoning or argument comes in different forms: ponendo ponens, tollendo tollens, among others, which are usually identified as a logical structure in which from a set of propositions considered as true–judgments–it is possible to obtain as a conclusion, a new proposition, that is to say, new knowledge.
具体而言，概念是基于现实中的对象、现象或过程所构建的知识；判断是一种逻辑命题，其内容是概念或概念间的关系，也就是说，它的内容就是知识；最后，推理或论证有不同的形式：肯定前件式、否定后件式等，它们通常被视为一种逻辑结构，在这种结构中，从一组被认为是真实的命题——判断——出发，能够得出一个新的命题作为结论，也就是新知识。

Theory of Activity

活动理论

The theory of activity (Leontiev, 1981) establishes that, in practical activity, people interact with the objects of reality and from them they apprehend their meanings; in other words, they construct knowledge about them.
活动理论（列昂节夫，1981）认为，在实际活动中，人们与现实中的事物相互作用，并通过这种相互作用领会事物的意义，即构建关于事物的知识。

Such activity–cognitive process–and in general any other, requires a set of actions and operations to be carried out.
这种活动（认知过程）及其他各类活动，都需要执行一系列的动作与操作。

According to this approach and that of the theory of knowledge, the process of knowing about the objects of reality can be identified with the process of concept formation (PCF) ².
根据活动理论与知识论的视角，对现实事物的认知过程可等同于“概念形成过程”（PCF）²。

² From now on, PCF stands for process of concept(s) formation.
注 2：后文均以 “PCF” 指代“概念形成过程”。

Rubinstein (1969) has identified the internal–theoretical–actions and operations of thought (IAOT) that carry out this process; these are analysis, abstraction, generalization and synthesis, and for their realization they can be supported by practical actions and operations:
鲁宾斯坦（1969）指出，执行这一过程的内在（理论性）思维动作与操作（IAOT）包括分析、抽象、概括与综合，而这些思维活动的实现可借助实际动作与操作的支持，具体如下：

• Analysis: consists in the breakdown of the object, phenomenon or process, in the clarification of its elements, features, parts, data or aspects, and in the determination of the dependencies or relations that may or may not be essential. By means of analysis we can differentiate the essential features, relations or operations from the incidental or inconsequential non-essential ones.
  分析：指对事物、现象或过程进行分解，明确其要素、特征、组成部分、数据或方面，并确定其中本质或非本质的依赖关系。通过分析，可区分本质特征、关系或操作与非本质的偶然特征、关系或操作。

• Abstraction: it consists of dispensing with the non-essential features but highlighting the essential and common ones to the objects studied. It is the mental process by which one passes from sensible qualities to abstract qualities.
  抽象：指摒弃非本质特征，同时突出所研究事物的本质共性特征。它是一种从可感知属性过渡到抽象属性的心理过程。

• Generalization: it originates mainly at the level of action. It consists in verifying whether the set of essential and common features abstracted can be extended to all the objects of the collection. In this operation, the extension of the concept is delimited, i.e., the class to which the objects that meet the generalized features can belong.
  概括：主要源于动作层面，指验证抽象出的本质共性特征是否可推广至该类别的所有事物。在这一操作中，会界定概念的外延，即符合该概括特征的事物所归属的类别。

• Synthesis: it is a theoretical mental action by which the object is reconstructed through the establishment of its essential characteristics. But this mental action is supported for its realization, in an external action, which consists in “crystallizing” or “depositing” ³ the meaning of the generalization produced, on a sensitive and concrete support–some representation–. That is to say, it can be represented in a definition, a proposition or a procedure, according to the type of abstracted and generalized features.
  综合：是一种理论性心理动作，通过确立事物的本质特征来重构该事物。但这种心理动作的实现需要借助外部动作的支持——将所产生的概括意义“固化”或“承载”上 ³。也就是说，根据抽象与概括特征的类型，综合结果可表现为定义、命题或步骤。

³ The use of the terms “crystallize” or “deposit” could be said to be out of context; however, they are used with the purpose of simplifying the discourse. Therefore, they will be used hereinafter even without quotation marks.
注 3：此处“固化（结晶）”或“承载（沉积）”虽看似与语境不符，但为简化表述，后文仍使用这两个术语，且不再加引号）到可感知的具体载体（如某种表征）

Process of Concept Formation

概念形成过程（PCF）

PCF is a cognitive process that takes place through IAOT: analysis, abstraction, generalization and synthesis (Majmutov, 1983).
PCF 是通过 IAOT（分析、抽象、概括、综合）实现的认知过程（马吉穆托夫，1983）。

From the teaching point of view, we will describe this process of knowing about objects, phenomena or processes of reality, making particular reference to PCF on a mathematical object (MO)⁴ with the support of Figure 2, emphasizing that the elements identified in the representation are essential within the same theory of knowledge.
从教学视角出发，本文将阐述对现实事物、现象或过程的认知过程，并结合图 2 重点说明数学对象的 PCF，同时强调表征中所识别的要素在知识论框架内具有本质意义。

⁴ From now on, MO stands for mathematical object(s).
注 4： 后文均以 MO 指代数学对象。

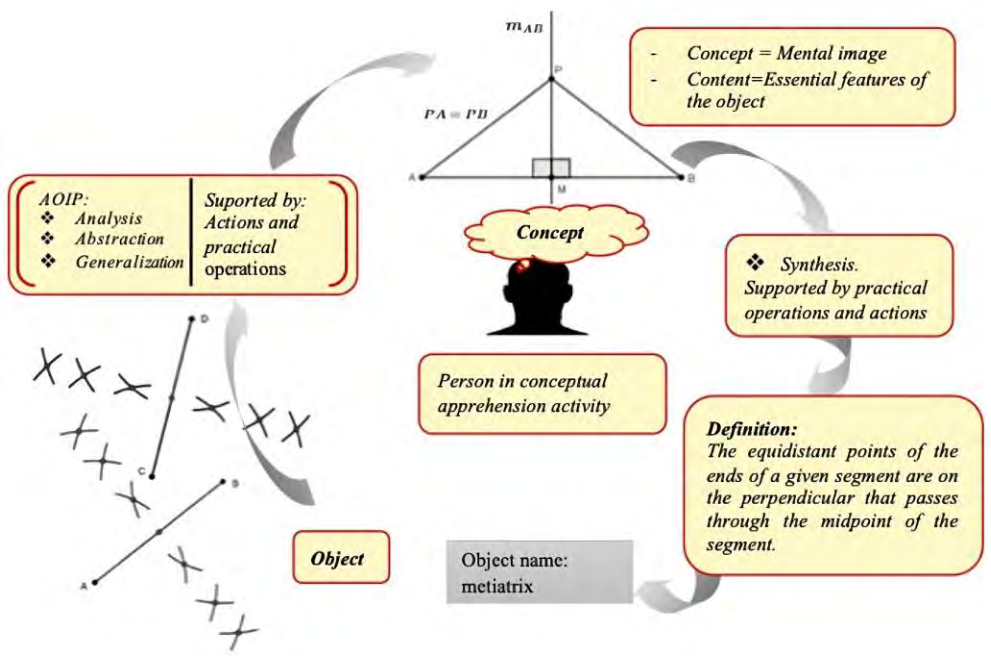
Figure 2. Concept formation process (Source: Authors’ own elaboration)

This process starts with the analysis of the representation of a situation outside the studied object; in fact, we have not built MO yet, so there can be no representation of it.
该过程始于对“待研究对象之外的情境表征”的分析；事实上，此时 MO 尚未构建，因此不存在其表征。

With the support of internal or external actions and operations, the analysis is performed to differentiate the features of the studied situation, in order to distinguish the essential ones from the non-essential ones.
在内在或外在动作与操作的支持下，通过分析区分所研究情境的特征，进而辨别本质特征与非本质特征。

By means of abstraction, we can dispense with the non-essential features and at the same time highlight the essential ones; this internal action can be supported by practical operations such as highlighting or coloring the essential features on the representation, or separating from the representation the features we wish to dispense with.
通过抽象，摒弃非本质特征并突出本质特征；这一内在动作可借助实际操作实现，例如在表征中标记或涂色突出本质特征，或从表征中剔除拟摒弃的特征。

If, when reviewing other similar situations, the previous features are presented, then it is possible to generalize them as essential and common features of a class of new objects.
若在考察其他类似情境时，上述特征均存在，则可将这些特征概括为某类新事物的本质共性特征。

As a result of the realization of these internal operations of thought, an image of a representative of this class of objects is formed in our mind; it is a mental image–concept about MO–formed on the basis of the essential and common features of the objects it represents.
通过执行这些内在思维操作，大脑中会形成该类事物的代表性意象；这一心理意象（即关于 MO 的概念）是基于其所代表事物的本质共性特征形成的。

In the final part of PCF, synthesis is the internal action of thought that reconstructs MO on the basis of its common and essential features; for its realization it relies on an external action, which consists in crystallizing or depositing the meaning of the produced generalization–knowledge built on MO–on a material representation, according to the type of abstracted and generalized features.
在 PCF 的最后阶段，综合是基于 MO 的共性本质特征重构 MO 的内在思维动作；其实现需依赖外在动作——根据抽象与概括特征的类型，将所产生的概括意义（即基于 MO 构建的知识）固化或承载到具象表征上。

But the features enlisted in the representation must be the same ones on which our mental image or concept about the constructed MO was formed.
但表征中所列出的特征，必须与构建 MO 的心理意象（或概念）所依据的特征一致。

Regarding this cognitive process, it is necessary to say that some authors, among them (Davýdov, 1982), designate in a summarized form the whole PCF with the term generalization.
关于这一认知过程，需说明的是：包括达维多夫（1982）在内的部分学者，将整个 PCF 简称为“概括”。

Thus, this term in this work will have two meanings: the first as one of the four IAOT that carry out PCF; and the second, as the entire cognitive process.
因此，本文中“概括”一词具有两层含义：一是作为执行 PCF 的四大 IAOT 之一；二是指代整个认知过程。

According to their form, generalizations can be recognized under different names: formulation of procedures, recognition of regularities, formulation of definitions, formulation of results, formulation of propositions, recognition of patterns, determination of invariant relations, among others.
从形式上看，概括可表现为不同形式：步骤制定、规律识别、定义表述、结果阐述、命题构建、模式识别、不变关系确定等。

According to their category, generalizations can be theoretical or empirical. When the teacher has been guiding and accompanying PCF on an MO, a specific way to evaluate the category of the generalizations produced by the students, it is necessary to keep in mind: If IAOT realizers of this cognitive process are supported by theoretical operations; or are produced on the basis of internal, essential and common features, it is a theoretical generalization. When IAOTs realizing PCF are supported by practical actions and operations; or are produced on the basis of external or non-essential features, it is an empirical generalization. When the teacher did not guide or accompany PCF on an MO, he/she cannot know under what conditions the generalization was formed or produced; therefore, a specific way to evaluate the category of generalizations consists in reviewing the arguments used to assert them: theoretical, if the arguments used to support them are based on the essential internal features, that is, on a theoretical basis. Empirical, when the arguments offered to assert them are based on non-essential external features, or on beliefs, or when an object does not fall within the generalization volume of the concept, and yet is assumed to have the property of the objects within the generalization volume, i.e., on an empirical basis.
从类别上看，概括可分为理论性概括与经验性概括。若教师已指导并参与 MO 的 PCF，则评估学生所产生概括的类别时需注意：若执行该认知过程的 IAOT 得到理论操作的支持，或基于内在本质共性特征产生，则为理论性概括；若执行 PCF 的 IAOT 得到实际动作与操作的支持，或基于外在非本质特征产生，则为经验性概括。若教师未指导或参与 MO 的 PCF，则无法知晓概括形成的条件，此时评估概括类别的方法是考察支撑概括的依据：若依据基于内在本质特征（即理论依据），则为理论性概括；若依据基于外在非本质特征、主观信念，或假设“不属于概念概括范围的事物具有该范围内事物的属性”（即经验依据），则为经验性概括。

Depending on the type of characteristic of MO under study, generalizations–concepts–can be classified into three types: concepts about objects, about operations, or about relations (Ballester, 1992; Jungk, 1985).
根据所研究 MO 特征的类型，概括（概念）可分为三类：对象类概念、操作类概念、关系类概念（巴列斯特，1992；荣克，1985）。

• Concepts about objects designate classes of real or ideal objects, which can be characterized by means of representatives. Examples: Triangle, quadrilateral, angle, number, etc.
  对象类概念：指代现实或理想对象的类别，可通过代表性事物描述。例如：三角形、四边形、角、数等。

• Concepts about operations designate actions that are performed with objects. Examples: bisection of an angle, addition, multiplication, etc.
  操作类概念：指代对对象执行的动作。例如：角的二等分、加法、乘法等。

• Concepts about relations reflect the existing relation between objects. Examples: perpendicularity, parallelism, congruence, Pythagorean relation, proportionality, among others.
  关系类概念：反映对象之间的现有关系。例如：垂直、平行、全等、勾股关系、比例关系等。

Figure 3. Stages of knowledge in construction process according to materialist view of theory of knowledge (Source: Authors’ ownelaboration)

Based on the principle assumed here–to apprehend is to know–, on the orientations from the materialistic point of view of the theory of knowledge, on the focus on the theory of activity and the own vision of the authors of this work, a didactic perspective for teaching, in particular of the concepts on MOs (DPTCMO)⁵ is formulated; whose structure considers the three stages in the process of construction of mathematical knowledge, according to the theoretical elements that sustain it (Figure 3).
基于本文所采用的“领会即认知”原则、知识论的唯物主义视角、活动理论的核心观点及作者自身的见解，本文构建了“数学对象概念教学视角”（DPTCMO）。该视角的结构依据其理论支撑要素，包含数学知识构建过程的三个阶段（见图 3）。

⁵ DPTCMO means didactic perspective for the teaching of concepts about mathematical objects.
注 5：后文均以“DPTCMO”指代“数学对象概念教学视角”

Thus, the process of construction of mathematical knowledge from such a perspective begins in the concrete with an empirical stage in which mental or theoretical operations are supported by practical operations–measuring, moving, superimposing, comparing, among others–that can be performed on representations in general, producing empirical generalizations.
因此，从该视角来看，数学知识的构建过程始于具象的经验阶段：在此阶段，心理或理论操作得到实际操作（如测量、移动、叠加、比较等）的支持，这些实际操作可作用于各类表征，进而产生经验性概括。

The passage from the concrete to the abstract will occur at the moment when the same generalization is obtained through the realization of mental or theoretical operations supported on theoretical principles–as a logical consequence derived from mathematical principles–.
从具象到抽象的过渡，发生在“通过基于理论原则的心理或理论操作（即作为数学原则推导的逻辑结果）获得相同概括”的时刻。

This second–formal–stage is the mathematical demonstration or deduction, and its function in this process consists in assuring as valid the knowledge produced in the first stage or transforming its category from empirical to theoretical.
第二个阶段（形式阶段）是数学证明或演绎，其作用是验证第一阶段产生知识的有效性，或将其类别从经验性转化为理论性。

The third stage of application of knowledge corresponds to the passage from the abstract to the concrete; it will occur at the moment when a field of application of the validated knowledge is found in practical activity.
第三个阶段（知识应用阶段）对应从抽象到具象的过渡：当在实际活动中找到已验证知识的应用领域时，该阶段便会启动。

Of course, knowledge is also constructed in the step called from the abstract to the abstract–applications of knowledge within mathematics–, in this case, IAOT, supported by previous results, can generate and validate new knowledge, which can then go from the abstract to the concrete.
当然，知识也会在“从抽象到抽象”的过程中构建（即数学领域内的知识应用）：在此过程中，IAOT 在已有成果的支持下，可生成并验证新知识，而这些新知识随后也可从抽象过渡到具象。

Methodology of mathematics teaching (Ballester, 1992; Hernández-Gómez et al., 2019; Jungk, 1985) reflects in part this perspective, when it points out that with respect to the treatment of concepts about MO, two ways can be distinguished in general:
数学教学法（巴列斯特，1992；埃尔南德斯-戈麦斯等人，2019；荣克，1985）在一定程度上体现了这一视角，它指出，对于 MO 概念的处理，总体可分为两种方式：

• Deductive: whoever goes through this way, his process of knowledge construction, begins with the presentation of the generalization that describes the object of knowledge, that is, the representation–in some of its forms–of MO of which he wants to know. In this process, internal or theoretical actions and operations are supported by external or practical actions and operations; the latter are performed on such representation, through the use of examples–and counter-examples–, seeking to apprehend the meaning of the knowledge about MO, deposited in the representation, that is, to realize the common and essential features of the object, and it is expected that, upon achieving such meaning, the same generalization from which it started, can be established.
  演绎式：采用该方式时，知识构建过程始于对“描述认知对象的概括”的呈现，即呈现待认知 MO 的某种表征。在此过程中，内在或理论性动作与操作得到外在或实际动作与操作的支持——后者通过举例（及反例）作用于该表征，旨在领会表征中所承载的 MO 相关知识的意义，即识别事物的共性本质特征；且期望在领会该意义后，能够回归并确立最初呈现的概括。

• Inductive way, by means of this process the activity of generalizing is carried out by making use of internal or theoretical actions and operations, supported by external or practical actions and operations. The meaning of the generalization–empirical– product of this process is crystallized or deposited in some representation–definition, proposition, method–. Next, the empirical generalization obtained is subjected to a formalization process in which theoretical actions and operations are supported by theoretical principles through deduction or mathematical demonstration, to ensure that the constructed knowledge is valid and change its category from empirical to theoretical generalization.
  归纳式：采用该方式时，概括活动通过“得到外在或实际动作与操作支持的内在或理论性动作与操作”实现。该过程产生的经验性概括的意义，会被固化或承载到某种表征（定义、命题、方法）中。随后，所获得的经验性概括会经历形式化过程：在此过程中，理论性动作与操作通过演绎或数学证明得到理论原则的支持，以验证所构建知识的有效性，并将其类别从经验性概括转化为理论性概括。

The deductive way has been used in the teaching of mathematics with greater insistence, but here we are interested in testing the inductive way, considering first, that it favors the regulation of the process of formation of IAOT in students; and second, that it may be closer to the real process of construction of mathematical knowledge.
演绎式在数学教学中应用更为广泛，但本文倾向于探讨归纳式，原因有二：一是它有助于引导学生形成 IAOT；二是它可能更贴近数学知识构建的实际过程。

Consequently, from DPTCMO that we are formulating, the inductive way in the cognitive processes on MO, allows to establish three stages for its realization according to Figure 3:
因此，基于本文构建的 DPTCMO，MO 认知过程中的归纳式可依据图 3 分为三个实现阶段：

1. The empirical stage: in which generalizations are produced from internal or theoretical actions and operations supported by external or practical actions and operations. The generalizations resulting from this stage are always empirical.
   经验阶段：通过“得到外在或实际动作与操作支持的内在或理论性动作与操作”产生概括，此阶段的概括均为经验性概括。

2. The formal or theoretical stage: in this stage, empirical generalizations undergo a formalization process in which a change of knowledge category can occur, from empirical to theoretical. The internal or theoretical actions and operations necessary for the realization of this process are based on theoretical principles–as a logical consequence derived from mathematical principles–. In other words, it is about mathematical deduction or demonstration, whose function in the process of construction of mathematical knowledge is to assure or validate empirical knowledge.
   形式（理论）阶段：经验性概括在此阶段经历形式化过程，知识类别可能从经验性转化为理论性。实现该过程所需的内在或理论性动作与操作，基于理论原则（即数学原则推导的逻辑结果）。换言之，该阶段核心是数学演绎或证明，其在数学知识构建过程中的作用是验证经验性知识的有效性。

3. Application of the constructed knowledge: this knowledge together with the previous validated results, applied to new situations can give rise to new knowledge: Within mathematics, generalizing new features for the concept on the newly formed MO, making possible its development; or producing a new generalization. In other disciplines, new generalizations may be produced to solve some problem of practical activity, among other possibilities.
   已构建知识的应用：将该知识与以往已验证成果结合并应用于新情境，可产生新知识：在数学领域内，可为新形成 MO 的概念概括新特征（推动概念发展），或产生新的概括；在其他学科领域，可产生新概括以解决实际活动中的问题等。

Exemplification Of Implementation Of Formulated Didactic Perspective

所构建教学视角的应用示例

Concept on Object

对象类概念

Empirical stage–Activities

经验阶段——活动设计

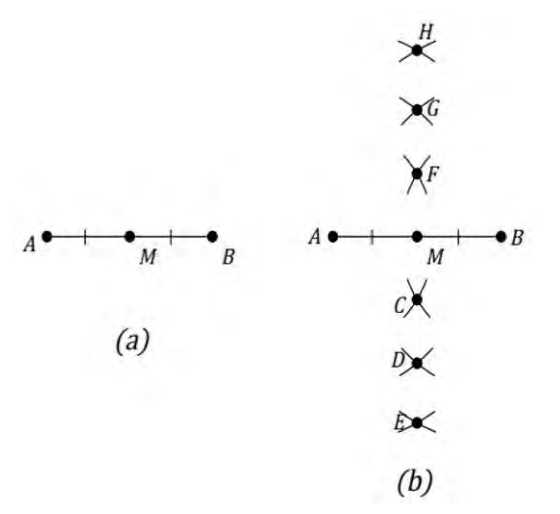
Figure 4. Approach to representation of object (Source: Authors’ own elaboration)

Activity 1:

活动 1：

In part a in Figure 4, a segment $AB$ and its midpoint $M$ are given. With the compass determine the location of several points on either side of $AB$ that satisfy the property of being equidistant from the ends of the segment. Does the midpoint $M$ satisfy this property?
图 4 的 a 部分给出了线段 $AB$ 及其中点 $M$ 。用圆规在 $AB$ 两侧确定若干满足“到线段两端点距离相等”这一性质的点。中点 $M$ 是否满足该性质？

Activity 2:

活动 2：

In part b in Figure 4, some points equidistant from the ends of $AB$ are represented, with the help of a ruler join those points–one by one–. What kind of line do you think it is? What angle–can you measure it–does it form with the segment $AB$ ?
图 4 的 b 部分呈现了若干到 $AB$ 两端点距离相等的点，用直尺将这些点逐一连接。你认为所形成的线是什么类型的线？该线与线段 $AB$ 形成的角（可测量）是多少度？

In this case, the above questions are only intended to guide the analysis of the object of study, with the support of different practical operations.
在本活动中，上述问题仅旨在借助不同实际操作，引导对研究对象的分析。

As a product of this analysis, it is possible to notice some outstanding features: apparently, a straight line is formed by joining the equidistant points of the ends of the segment, it forms a right angle with the segment and passes through its midpoint.
通过分析可发现一些显著特征：连接到线段两端点距离相等的点，显然会形成一条直线；该直线与线段垂直，且经过线段的中点。

Regarding the action of abstraction, in this case there is nothing to be dispensed with, so the above features are abstracted in their entirety.
从抽象动作来看，本案例中无需摒弃任何特征，因此需完整抽象上述所有特征。

By checking whether these features can be extended to new similar situations, they can be generalized as essential features common to all similar objects studied.
通过验证这些特征是否可推广到新的类似情境，可将其概括为所有类似研究对象的本质共性特征。

In synthesis, we can crystallize or deposit the meaning of the knowledge acquired about such objects in some form of language, that is, in a representation.
通过综合，可将关于该类对象的已有知识意义，以某种语言形式（即某种表征）固化或承载下来。

In other words, we can formulate a definition–a written verbal expression–in which the substantial features of the defining object are listed:
换言之，可构建一个定义（书面文字表述），列出所定义对象的本质特征：

The equidistant points of the ends of a given segment are on the perpendicular that passes through the midpoint of the segment. Moreover, this special straight line can be called by the term mediatrix of a segment.
给定线段两端点距离相等的点，位于经过该线段中点的垂直线上。此外，这条特殊的直线可称为“线段的垂直平分线”（mediatrix of a segment）。

We must be aware that MO only exist at the conceptual level, as has been pointed out, it is the mental image that we form on the basis of its internal or essential and common features, the same ones that appear in the representation.
需明确的是，如前文所述，MO 仅存在于概念层面，它是基于对象内在本质共性特征（与表征中呈现的特征一致）形成的心理意象。

But the written verbal expression we have chosen to crystallize the meaning of the knowledge built on the mediator is one of its material representations.
而我们选择的、用于固化“垂直平分线”相关知识意义的书面文字表述，只是其具象表征之一。
Therefore, MO should not be confused with its representation.
因此，不应将 MO 与其表征混淆。

Formal stage–Activities

形式阶段——活动设计

The previous generalization has the category of empirical, since even when it has been produced through IAOT, these were supported by operations of a practical type–visual perception of the line that joins the points as a straight line, measurement of the angle it forms with the segment–.
上述概括属于经验性概括，因为尽管它是通过 IAOT 产生的，但这些 IAOT 得到了实际操作的支持——如通过视觉感知判断“连接各点的线为直线”、通过测量确定“该线与线段形成的角”。

And although so far it is not a certain knowledge, there is a strong suspicion that it may be true.
尽管目前该知识尚未得到证实，但有充分理由推测其真实性。

Therefore, it is necessary to move on to the formal stage of this process of knowledge construction in which we will seek to obtain the same generalization as before, but without the aid of practical operations, but with the support of theoretical principles.
因此，需进入知识构建的形式阶段：在此阶段，将在不借助实际操作、仅依靠理论原则的前提下，尝试获得与之前相同的概括。

This process can be achieved through mathematical deduction or demonstration.
该过程可通过数学演绎或证明实现。

Thus, the previous generalization will change its category from empirical to theoretical; it will become part of the set of principles of the theory and subsequently, it can be used in processes of formalization of mathematical knowledge.
由此，上述概括的类别将从经验性转化为理论性，并成为理论原则体系的一部分，进而可用于数学知识的形式化过程。

Activity 3:

活动 3：

A first objective in this activity is to know if the line that passes through the points–located by practical operations– equidistant from the ends of the segment $AB$ is indeed a straight line. The analysis must be guided by our suspicion that the mentioned points are on a line.
本活动的首要目标是验证“通过实际操作确定的、到线段 $AB$ 两端点距离相等的点所连成的线”是否为直线。分析需基于“上述点共线”这一假设展开。

We know that there is always a line that passes through two given points, so that, if a line is drawn through two of the points that satisfy the property of being equidistant from the ends of the segment, it would only be necessary to prove that the others are also on that line.
已知两点确定一条直线，因此，若过两个“到线段两端点距离相等”的点作一条直线，只需证明其他同类点也在该直线上即可。

Figure 5. Representation of situation (Source: Authors’ own elaboration)

Based on part a in Figure 5, we realize that by tracing the line $l$ through $M$ and $F$ , two triangles $\Delta 1$ and $\Delta 2$ are formed, which are congruent, since they have their three sides, respectively equal; consequently their angles $\alpha$ and $\beta$ are equal because they are corresponding parts of congruent figures. Moreover, if these are collinear, $\alpha +\beta =180^{\circ }$ , then $\alpha =\beta =90^{\circ }$ . This guarantees that the line $l$ is perpendicular to the segment $AB$ at its midpoint $M$ .
基于图 5 的 a 部分可知，过 $M$ 和 $F$ 作直线 $l$ ，会形成 $\Delta 1$ 和 $\Delta 2$ 两个三角形。由于这两个三角形三边对应相等，因此全等；其对应角 $\alpha$ 和 $\beta$ 也相等。此外，若 $\alpha$ 与 $\beta$ 共线，则 $\alpha +\beta =180^{\circ }$ ，进而可得 $\alpha =\beta =90^{\circ }$ 。这表明直线 $l$ 垂直于线段 $AB$ 且经过其中点 $M$ 。

In part b in Figure 5, we have already recorded the fact that $l\perp AB$ and that it passes through $M$ . Now, as the second objective of the activity, we are interested in proving that the other points with the property of being equidistant from the ends of $AB$ are also on $l$ ; to perform the analysis we will take any point with that property and try to prove the following proposition:
图 5 的 b 部分已证实 $l\perp AB$ 且 $l$ 过 $M$ 。本活动的第二个目标是证明“其他到 $AB$ 两端点距离相等的点也在 $l$ 上”：选取任意一个具有该性质的点，尝试证明以下命题：

Proposition (A): If $l\perp AB$ at its midpoint $M$ , and $G$ is any point with the property of being equidistant from the ends of the segment $AB$ , then $G$ is on $l$ .
命题（A）：若直线 $l$ 在线段 $AB$ 的中点 $M$ 处与 $AB$ 垂直，且点 $G$ 是任意一个到 $AB$ 两端点距离相等的点，则 $G$ 在 $l$ 上。

Before performing the proof, it is necessary to open a space to discuss two principles of mathematical theory about any logical proposition. We begin by saying that given any logical proposition ($P$), there are three possibilities regarding its truth value: a) $P$ is true; b) its negation is true, or c) both are true at the same time
在进行证明之前，有必要先开辟一个空间来讨论数学理论中关于任意逻辑命题的两个原则。首先，对于任意给定的逻辑命题（$P$），关于其真值存在三种可能性：a）$P$为真；b）其否定为真；或者c）两者同时为真

{ a) P ( V ) b) ∼ P ( V ) c) { P ∧ ∼ P } ( V ) → a) P ( V ) b) ∼ P ( V ) \left\{ \begin{array}{lll} \text{a)} & P & (V) \\ \text{b)} & \sim P & (V) \\ \text{c)} & \{P \land \sim P\} & (V) \end{array} \right. \quad \to \quad \begin{array}{ll} \text{a)} & P \quad (V) \\ \text{b)} & \sim P \quad (V) \end{array} ⎩ ⎨ ⎧​a)b)c)​P∼P{P∧∼P}​(V)(V)(V)​→a)b)​P(V)∼P(V)​

But on the basis of the following principle:
但基于以下原则：

Non-contradiction: Mathematical theory does not admit any contradiction in its discourse. The third of the above options has to be excluded–third excluded–, since it represents a contradiction, leaving the first two possibilities.
不矛盾律：数学理论在其论述中不承认任何矛盾。上述第三种可能性必须被排除——排中——因为它代表了一种矛盾，于是就只剩下前两种可能性。

In short, this is expressed in the following principle:
简而言之，这体现在以下原则中：

Excluded third: Given a logical proposition, it is either true or its negation is true.
排中律：给定一个逻辑命题，它要么为真，要么其否定为真。

Such principles are the basis of the method of demonstration called reductio ad absurdum. This consists in assuming as true the negation of the thesis $\neg T$ corresponding to the proposition to be proved; but if this assumption leads us through logical reasoning to a mathematical contradiction, we must be aware that we will have to discard this assumption $\neg T$ to avoid the contradiction, that is, it is not possible to sustain it as true; consequently, based on the principle of the excluded third, only the option that $T$ is true remains.
这些原则是“反证法”（reductio ad absurdum）的基础。反证法的步骤为：假设待证明命题的论题的否定 $\neg T$ 为真；若该假设通过逻辑推理导致数学矛盾，则需摒弃 $\neg T$ 以避免矛盾（即 $\neg T$ 无法成立）；因此，根据排中律，仅剩下“论题 $T$ 为真”这一种可能。

We will use this method of demonstration to perform the formal proof on the validity of the empirical generalization obtained above. That is, we will assume as true the negation of the thesis corresponding to proposition (A): $\neg T$ : $G$ is not on $l$ .
下文将采用反证法，对上述经验性概括的有效性进行形式化证明。即假设命题（A）的论题的否定为真： $\neg T$ ：点 $G$ 不在直线 $l$ 上。

And we will make the analysis based on part b in Figure 5. From the point $G$ located outside $l$ we plot the distances to the ends of $AB$ and the line $GM$ . With this, two triangles $\Delta 3$ and $\Delta 4$ are formed, which turn out to be congruent by having their three sides, respectively equal; consequently their angles $\delta =\epsilon$ being corresponding parts of congruent figures. Moreover, their sum $\delta +\epsilon =180^{\circ }$ because they are collinear, therefore $\delta =\epsilon =90^{\circ }$ , which means that $GM\perp AB$ at $M$ . This constitutes a contradiction with the principle that states that through a point $M$ on a straight line $AB$ passes a single perpendicular to that line.
基于图 5 的 b 部分进行分析：过直线 $l$ 外的点 $G$ ，分别连接 $G$ 与 $A$ 、 $G$ 与 $B$ （即点 $G$ 到 $AB$ 两端点的距离），并连接 $GM$ 。由此形成 $\Delta 3$ 和 $\Delta 4$ 两个三角形——由于三边对应相等，这两个三角形全等，因此其对应角 $\delta =\epsilon$ 。此外，因 $\delta$ 与 $\epsilon$ 共线，故 $\delta +\epsilon =180^{\circ }$ ，进而可得 $\delta =\epsilon =90^{\circ }$ ，即 $GM\perp AB$ 于 $M$ 。这与“过直线 $AB$ 上一点 $M$ 有且仅有一条直线与 $AB$ 垂直”的原则矛盾。

As said, the assumption of $\neg T$ : $G$ is not on $l$ as true causes a contradiction and it is not possible to hold it as true. Consequently, based on the excluded third principle, $T$ : $G$ is on $l$ is true, which concludes the proof.
如前所述，“ $\neg T$ （点 $G$ 不在直线 $l$ 上）为真”的假设会导致矛盾，因此该假设不成立。根据排中律，“ $T$ （点 $G$ 在直线 $l$ 上）为真”，证明完毕。

Similar proofs could be performed for each point with such property, but this is no longer necessary, since in the proof performed any point with the property was considered and this allows to generalize the feature of belonging to the line $l$ for points equidistant from the ends of the segment $AB$ .
虽可对每个具有该性质的点进行类似证明，但无需如此——因为上述证明已选取“任意一个具有该性质的点”，因此可将“到线段 $AB$ 两端点距离相等的点都在直线 $l$ 上”这一特征进行概括。

In summary, an expression can be formulated to crystallize the meaning of the constructed knowledge: The points equidistant from the ends of a given segment are on the perpendicular that passes through the midpoint of the segment. Moreover, this special line can be denoted by the term mediatrix of a segment.
综上，可构建如下表述以固化所构建知识的意义：给定线段两端点距离相等的点，位于经过该线段中点的垂直线上。此外，这条特殊的直线可称为“线段的垂直平分线”。

Let us emphasize two aspects. On the one hand, the generalization produced in the formal stage has the same form as that obtained in the empirical stage, but differs in one aspect: it now has the category of theoretical knowledge, since it was obtained in a formalization process by means of mathematical deduction or demonstration. This change exemplifies the passage from the concrete to the abstract in relation to the process of knowledge construction, according to the Marxist point of view.
需强调两点：一方面，形式阶段产生的概括与经验阶段的概括形式相同，但类别不同——前者属于理论性知识，因为它是通过数学演绎或证明的形式化过程获得的。这一转变体现了马克思主义视角下知识构建过程中“从具象到抽象”的过渡。

On the other hand, when reviewing the statement of the previous immediate generalization, even though it already has the category of theoretical knowledge, we notice that, although the equidistant points are on the mediatrix, we do not know if all its points have this property. And this is an aspect that can be of interest in the construction of knowledge about the perpendicular bisector of a segment. To find out, we propose the following activity:
另一方面，尽管上述概括已属于理论性知识，但需注意：该概括仅表明“到线段两端点距离相等的点在垂直平分线上”，尚未明确“垂直平分线上的所有点是否都具有该性质”。这是线段垂直平分线知识构建中需进一步探讨的问题。为解答该问题，设计如下活动：

Activity 4:

活动 4：

We want to know if all the points of the perpendicular bisector have the feature of equidistance to the ends of the segment. This can be solved by proving that any point on the perpendicular bisector has this property.
探究“垂直平分线上的所有点是否都具有‘到线段两端点距离相等’的性质”。可通过证明“垂直平分线上任意一点都具有该性质”来解答。

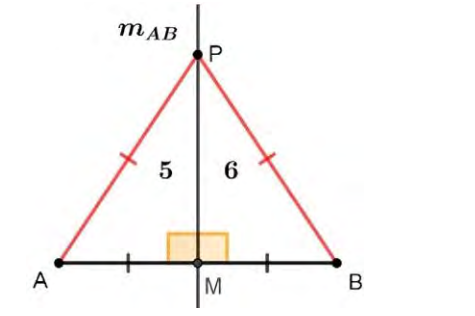
Figure 6. Mediatrix of segment 𝐴𝐵 (Source: Authors’ own elaboration)

In Figure 6, a segment $AB$ , its midpoint $M$ and its perpendicular bisector $m_{AB}$ are represented. If any point $P$ of this line is taken and its distances to the ends $A$ and $B$ are plotted, the right triangles $\Delta 5$ and $\Delta 6$ are formed, whose hypotenuses are the distances that we are interested in knowing if they are equal. One way to investigate this is to try to know if these triangles are congruent, because in that case the homologous parts–corresponding–are equal.
图 6 呈现了线段 $AB$ 、其中点 $M$ 及其垂直平分线 $m_{AB}$ 。取 $m_{AB}$ 上任意一点 $P$ ，连接 $PA$ 、 $PB$ （即点 $P$ 到 $A$ 、 $B$ 的距离），形成直角三角形 $\Delta 5$ 和 $\Delta 6$ ——这两个三角形的斜边即为待验证是否相等的距离。验证方法之一是判断这两个三角形是否全等：若全等，则其对应边（斜边）相等。

Without much difficulty, both teachers and students to whom this proposal is addressed can indeed conclude that these triangles are congruent and finally that the distances $PA$ and $PB$ are equal. Similar to the previous case, it will no longer be necessary to perform further tests for other points, since it was done for any point belonging to $m_{AB}$ .
无论是教师还是学生，都可较容易地得出“这两个三角形全等”的结论，进而推出 $PA=PB$ 。与前文类似，无需对其他点进行验证——因为已选取“垂直平分线 $m_{AB}$ 上的任意一点”进行证明。

In summary, we can use a written verbal representation to deposit the meaning of the constructed knowledge: All points on the perpendicular bisector of a given segment are equidistant from the ends of the segment.
综上，可通过如下书面文字表述固化所构建知识的意义：给定线段的垂直平分线上的所有点，到该线段两端点的距离相等。

The fact that both teachers and students successfully complete this test represents a development in their knowledge about this object, since they will have managed to incorporate a new feature to the mental image they had formed, that is, to their concept of the perpendicular bisector.
师生能够完成该验证，表明他们对“垂直平分线”这一对象的知识得到了发展——他们已将新特征融入之前形成的心理意象（即垂直平分线的概念）中。

Another factor for the development of a concept is related to the change in the category of knowledge. In order to continue with the development of the concept of the mediatrix, the following activity is proposed:
概念发展的另一影响因素与知识类别的转变相关。为进一步推进垂直平分线概念的发展，设计如下活动：

Activity 5:

活动 5：

Analyze the following situation represented in Figure 7: In the plane is given a segment $AB$ and its bisector $m_{AB}$ ; it is interesting to know if there is any point in the plane outside $m_{AB}$ that can have the feature of equidistance to the ends of $AB$ .
分析图 7 呈现的情境：平面内给定线段 $AB$ 及其垂直平分线 $m_{AB}$ ，探究“平面内是否存在不在 $m_{AB}$ 上但到 $AB$ 两端点距离相等的点”。

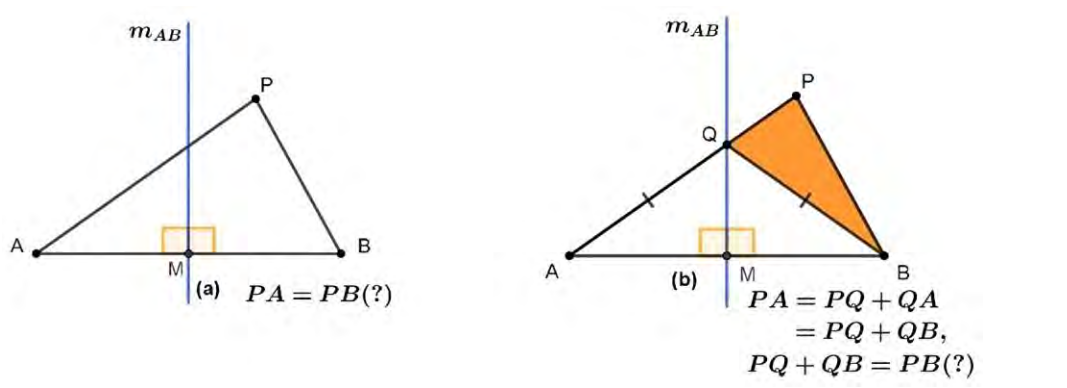
Figure 7. Representation & analysis of perpendicular bisector of segment 𝐴𝐵 (Source: Authors’ own elaboration)

In part a in Figure 7, we have taken any point $P$ in the plane outside $m_{AB}$ and plotted its distances to the ends of segment $AB$ . So finding out whether $P$ can have the feature of the points on the perpendicular bisector is equivalent to investigating whether $PA$ and $PB$ can be equal.
图 7 的 a 部分中，选取平面内不在 $m_{AB}$ 上的任意一点 $P$ ，连接 $PA$ 、 $PB$ （即点 $P$ 到 $AB$ 两端点的距离）。探究“点 $P$ 是否具有垂直平分线上点的性质”，等同于探究“ $PA$ 与 $PB$ 是否可能相等”。

In part b in Figure 7, the point $Q$ of intersection between $PA$ and $m_{AB}$ has been highlighted and the segment $QB$ has been drawn, thus forming the triangle $PQB$ . With the aid of this representation the following valid relation can be established:
图 7 的 b 部分中，标记出 $PA$ 与 $m_{AB}$ 的交点 $Q$ ，并连接 $QB$ ，形成三角形 $PQB$ 。借助该表征可建立如下有效关系：

Relation (1): Segments $PQ$ and $QA$ are collinear, then $PA=PQ+QA(1)$ . It is also satisfied that $Q\in m_{AB}$ , then $QA=QB(2)$ . Therefore, $PA=PQ+QB(3)$ . Consequently, investigating whether $PA=PB$ (?) is equivalent to knowing whether $PQ+QB=PB$ (?).
关系（1）：线段 $PQ$ 与 $QA$ 共线，因此 $PA=PQ+QA(1)$ ；又因 $Q\in m_{AB}$ ，故 $QA=QB(2)$ ；由此可得 $PA=PQ+QB(3)$ 。因此，探究“ $PA=PB$ 是否成立”，等同于探究“ $PQ+QB=PB$ 是否成立”。

In this regard, it is known that the shortest distance between two points is the line segment that joins them. This principle applied to any triangle gives rise to the modern expression called triangle inequality: the sum of two of any of its sides is always greater than the third. Applying this knowledge to the case of the triangle $PQB$ of part b in Figure 7, we have:
已知“两点之间线段最短”，该原则应用于任意三角形可得到“三角形不等式”：三角形任意两边之和大于第三边。将该知识应用于图 7b 部分的 $\Delta PQB$ ，可得：
Relation (2): In triangle $PQB$ , it is satisfied that $PQ+QB>PB$ ; and since $PA=PQ+QB(3)$ , then $PA>PB$ .
关系（2）：在 $\Delta PQB$ 中， $PQ+QB>PB$ ；结合 $PA=PQ+QB(3)$ ，可得 $PA>PB$ 。

This shows that any point $P$ in the plane outside $m_{AB}$ is not equidistant from the ends of $AB$ ; this allows us to generalize this feature for all points in the plane outside $m_{AB}$ and in synthesis to formulate an expression that crystallizes the meaning of the new knowledge constructed.
这表明，平面内不在 $m_{AB}$ 上的任意一点 $P$ ，到 $AB$ 两端点的距离都不相等；由此可将该特征概括到“平面内所有不在 $m_{AB}$ 上的点”，并通过综合构建如下表述，固化新构建知识的意义：
We could simply express: There is no point in the plane outside the perpendicular bisector that is equidistant from the ends of the segment. But first it was proved that all points on the perpendicular bisector have the feature of equidistance. With these two results a conclusion can be formulated: All points in the plane that are equidistant from the ends of a segment are on the segment’s perpendicular bisector.
可简化表述为：平面内不在垂直平分线上的点，到线段两端点的距离都不相等。结合前文已证明的“垂直平分线上所有点到线段两端点距离相等”，可得出结论：平面内到线段两端点距离相等的所有点，都在该线段的垂直平分线上。

This is another development factor for the concepts, which has to do with what we call generalization volume: in this case, it has been possible to generalize the feature of belonging to the perpendicular bisector to any point in the plane that has the property of equidistance to the ends of the given segment.
这是概念发展的另一影响因素，与“概括范围”相关：在本案例中，已将“属于垂直平分线”这一特征，概括到“平面内所有具有‘到给定线段两端点距离相等’性质的点”。

Concept of Operations

操作类概念

Empirical stage–Activities

经验阶段——活动设计

Up to this point of PCF on MO called the mediatrix of a segment, we can consider that the concept we have formed of this object is acceptable; that is, our mental image reflects its features: it is perpendicular and passes through the midpoint of the segment, and it contains all the points in the plane that are equidistant from the ends of the segment.
截至目前，关于“线段垂直平分线”这一 MO 的 PCF 已完成，我们所形成的该对象概念是合理的——心理意象已包含其核心特征：垂直于线段且经过其中点，且包含平面内所有到线段两端点距离相等的点。
But we still do not know how to draw it or construct it. Therefore, with the dual purpose of covering this absence and exemplifying PCF on operations, we will pose the following activity:
但尚未明确如何绘制或构建垂直平分线。因此，为填补这一空白并举例说明操作类概念的 PCF，设计如下活动：

Activity 6:

Given any segment $AB$ (Figure 8), trace its mediatrix $m_{AB}$ with a ruler and compass.
活动 6：给定任意线段 $AB$ （图 8），用直尺和圆规绘制其垂直平分线 $m_{AB}$ 。

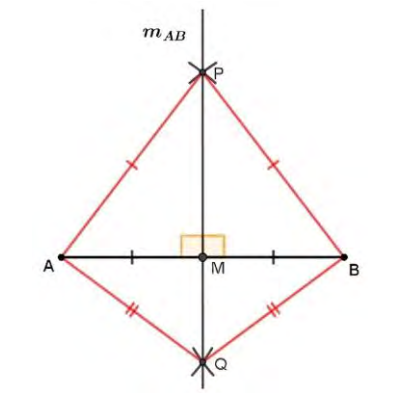
Figure 8. Representation of line of perpendicular bisector with ruler & compass (Source: Authors’ own elaboration)

Basis of activity orientation: Considering the knowledge built above, it can be established that:
活动指导依据：基于已构建的知识，可明确：

1. The mediatrix of a segment is a perpendicular line passing through its midpoint.
   线段的垂直平分线是经过线段中点的垂直线；

2. It contains all the points in the plane that are equidistant from the ends of the segment.
   垂直平分线包含平面内所有到线段两端点距离相等的点；

3. A single line passes through two given points.
   两点确定一条直线。

Based on the above, the following question was asked: If the location of two points equidistant from the ends of the given segment were known, would they be on the perpendicular bisector?
基于上述依据，提出问题：若已知两个“到给定线段两端点距离相等”的点，这两个点是否在该线段的垂直平分线上？

After considering the previous knowledge, as a product of the analysis, the need to locate two points equidistant from the ends of the segment $AB$ is highlighted, since the line that passes through them is the mediatrix sought.
结合已有知识，通过分析可明确：需确定两个“到线段 $AB$ 两端点距离相等”的点——因为过这两个点的直线即为所求的垂直平分线。

Thus, an effective procedure will be found. Then, the essential operations required to draw the perpendicular bisector can be abstracted.
由此可确定一套有效步骤，并抽象出绘制垂直平分线所需的核心操作。

Then it is checked if this set of operations–procedure–can be effective for any segment; if so, then it will be generalized, and we are in front of a PCF of operation.
随后验证该操作集合（步骤）是否对任意线段均有效：若有效，则可进行概括，此时便进入操作类概念的 PCF。

Unlike the concept on object, instead of writing a definition, the essential and common operations in all cases–method–to draw the perpendicular bisector of a given segment are described; in short:
与对象类概念不同，操作类概念无需构建定义，而是描述“在所有情况下绘制给定线段垂直平分线的核心共性操作（方法）”，具体如下：

Method to draw the perpendicular bisector of a given segment (with ruler and compass):
用直尺和圆规绘制给定线段垂直平分线的方法：

1. Locate two points equidistant from the ends of the segment.
   确定两个到线段两端点距离相等的点；
2. The straight line passing through these two points is the requested perpendicular bisector.
   过这两个点作直线，该直线即为所求的垂直平分线。

Formal stage–Activities

形式阶段——活动设计

At this point, it can be said that the generalization–method–produced is empirical.
此时，上述概括（方法）属于经验性概括。

To change its category to theoretical knowledge, teachers or students are required to show formal arguments–based on theoretical principles of mathematics–that assure that with the described procedure the perpendicular bisector of a segment is always obtained.
要将其类别转化为理论性知识，师生需提供基于数学理论原则的形式化依据，以证明“通过上述步骤可始终得到线段的垂直平分线”。

For example, based on Figure 8, the following result is established and obtained:
例如，基于图 8 可建立并得到如下结论：

Proposition (B): $P$ and $Q$ are equidistant from the ends of $AB$ ; two points determine a single line; moreover, the mediatrix contains all points equidistant from the ends of $AB$ . Then, the line through $P$ and $Q$ is $m_{AB}(\ast )$ .
命题（B）：点 $P$ 、 $Q$ 到 $AB$ 两端点距离相等；两点确定一条直线；且垂直平分线包含所有到 $AB$ 两端点距离相等的点。因此，过 $P$ 、 $Q$ 的直线即为 $m_{AB}(\ast )$ 。

The result of $(\ast )$ is the formal proof that the line through $P$ and $Q$ is the requested perpendicular bisector, and its justification did not require any practical operation.
结论 $(\ast )$ 从形式上证明了“过 $P$ 、 $Q$ 的直线即为所求垂直平分线”，且该证明无需任何实际操作的支持。

Applications of Constructed Knowledge: Inside Mathematics & Practice Problems

已构建知识的应用：数学领域内与实际问题

Activity 7

活动 7

The problem of finding a point equidistant from three other non-collinear given points $A$ , $B$ , and $C$ (part a & part b in Figure 9) can be seen as a PCF of operation: method for locating a point equidistant from three other non-collinear given points.
“寻找一个到三个不共线已知点 $A$ 、 $B$ 、 $C$ 距离相等的点”这一问题（图 9 的 a、b 部分），可视为操作类概念的 PCF，即“确定到三个不共线已知点距离相等的点的方法”。

Figure 9. Representation of point equidistant from three other non-collinear points (Source: Authors’ own elaboration)

If we pose it to students who have recently formed the concept of mediatrix of a segment, then, in the analysis of the situation, they will try some procedures $P_1,P_2,P_3,\cdots$ that will not lead them to the solution.
若将该问题呈现给刚形成“线段垂直平分线”概念的学生，他们在分析情境时，可能会尝试一些无法解决问题的步骤（如 $P_1,P_2,P_3,\cdots$ ）。

This is a good moment to guide their activity, pointing out that sometimes it is convenient to break down a complex situation into simpler ones to facilitate the task of analysis; that is , if in this case the requirement is to find a point equidistant from three others, we can first suggest finding a point equidistant from only two.
此时是引导学生活动的最佳时机，可提示他们：有时将复杂情境拆解为简单情境，能更轻松地完成分析——即在本问题中，若需求是“找一个到三个点距离相等的点”，可先尝试“找一个到两个点距离相等的点”。

With this suggestion and the knowledge they have built up, they will be more likely to solve the problem posed.
结合这一提示与已构建的知识，学生更有可能解决该问题。

Thus, they will find a procedure $P_k$ that is effective, such as tracing the perpendicular bisectors $m_{AB}$ and $m_{BC}$ , whose intersection determines the point $K$ that is equidistant from $A$ , $B$ , and $C$ as required.
最终，他们会找到有效的步骤 $P_k$ ：绘制线段 $AB$ 的垂直平分线 $m_{AB}$ 与线段 $BC$ 的垂直平分线 $m_{BC}$ ，两条垂直平分线的交点 $K$ 即为所求的“到 $A$ 、 $B$ 、 $C$ 距离相等的点”。

Then, by abstraction, the erroneous procedures are dispensed with and the procedure $P_k$ is adopted.
随后通过抽象，摒弃无效步骤，保留有效步骤 $P_k$ 。

Then it is checked if this procedure can be effective for any trio of non-collinear points; if so, then it will have been generalized, and we are in front of an operation PCF.
接着验证该步骤是否对任意三个不共线点均有效：若有效，则可进行概括，此时便完成了操作类概念的 PCF。

Unlike the concept on object, instead of writing a definition, the essential and common operations in all cases–method–are described to determine the position of the point equidistant from three other given non-collinear points. In summary, the method is as follows:
与对象类概念不同，操作类概念无需构建定义，而是描述“在所有情况下确定‘到三个不共线已知点距离相等的点’的核心共性操作（方法）”，具体如下：

Method to locate a point equidistant from three other given non-collinear points $A$ , $B$ , and $C$ (with ruler and compass):
用直尺和圆规确定“到三个不共线已知点 $A$ 、 $B$ 、 $C$ 距离相等的点”的方法：

1. Draw the perpendicular bisector of $AB$
   绘制线段 $AB$ 的垂直平分线；

2. Draw the perpendicular bisector of $BC$ .
   绘制线段 $BC$ 的垂直平分线；

3. The intersection $K$ of both perpendicular bisectors is the point we are looking for.
   两条垂直平分线的交点 $K$ 即为所求的点。

At this point in the development of the knowledge construction process, it can be said that the generalization–method–produced is empirical.
在知识构建过程的这一阶段，上述概括（方法）仍属于经验性概括。

To change its category to theoretical knowledge, students are required to show formal arguments–based on theoretical principles of mathematics–that assure that with the described procedure a point with the requested property is always obtained.
要将其类别转化为理论性知识，学生需提供基于数学理论原则的形式化依据，以证明“通过上述步骤可始终得到具有所求性质的点”。

For example, based on part b in Figure 9, the following result is obtained: since $K\equiv m_{AB}\cap m_{BC}$ , then $K$ is on both perpendicular bisectors. Furthermore, if $K$ is on the perpendicular bisector $m_{AB}$ , then $KA=KB$ ; analogously, if $K$ is on the perpendicular bisector $m_{BC}$ , then $KB=KC$ . Therefore, $KA=KB=KC(\ast \ast )$ .
例如，基于图 9 的 b 部分可得到如下结论：因 $K$ 是 $m_{AB}$ 与 $m_{BC}$ 的交点（ $K\equiv m_{AB}\cap m_{BC}$ ），故 $K$ 同时在两条垂直平分线上。又因 $K$ 在 $m_{AB}$ 上，故 $KA=KB$ ；同理， $K$ 在 $m_{BC}$ 上，故 $KB=KC$ 。因此， $KA=KB=KC(\ast \ast )$ 。

The result $(\ast \ast )$ is the formal proof that $K$ is equidistant from the three given points $A$ , $B$ , and $C$ , and its justification did not require any practical type of operation.
结论 $(\ast \ast )$ 从形式上证明了“ $K$ 到三个已知点 $A$ 、 $B$ 、 $C$ 距离相等”，且该证明无需任何实际操作的支持。

If any student insists on defending the validity of his generalization supported by practical operations, it is an indicator that his concept–method–still remains in the category of empirical knowledge.
若有学生仍坚持通过实际操作来证明该概括的有效性，则表明其“方法”概念仍停留在经验性知识范畴。

Activity 8

活动 8

A new problem related to the result of the previous situation can be posed, which consists of knowing if it is possible to draw a circle passing through three given non-collinear points, and if possible, how many such circles can pass through these three points.
基于前文结果，可提出新问题：是否存在经过三个不共线已知点的圆？若存在，这样的圆有多少个？
The problems described in Activity 7 and Activity 8 can be considered as activities corresponding to the passage from the abstract to the abstract of validated knowledge about the mediatrix object; that is, they are applications of knowledge within mathematics.
活动 7 与活动 8 所描述的问题，可视为“垂直平分线”相关验证知识“从抽象到抽象”的应用活动，即数学领域内的知识应用。
But as it has been said, there can also be applications outside mathematics, in practical activities, as proposed in Activity 9, which is designed as an independent work activity.
但如前文所述，知识也可应用于数学领域之外的实际活动，活动 9 便为此设计，可作为自主作业。

Activity 9

活动 9

A neighbor asked a blacksmith to install a sliding gate. But the gate is too wide, and when it opens, it may collide with the adjacent wall. To avoid this problem, it is necessary to bend a part of the rail on which the gate runs into the shape of a circular arc.
某居民请铁匠安装一扇推拉门，但门体过宽，开门时可能会撞到旁边的墙。为避免这一问题，需将门运行的轨道一部分弯成圆弧形状。

Figure 10. Representation of study situation (Source: Authors’ own elaboration)

Figure 10 shows the outline of the project, where three points $A$ , $B$ , and $C_1$ are marked; these points should determine the size and curvature of the circular arc needed to make the mold for shaping that part of the rail.
图 10 呈现了该项目的设计草图，其中标记了三个点 $A$ 、 $B$ 、 $C_1$ ——这三个点需用于确定圆弧的尺寸与曲率，以便制作轨道该部分的成型模具。

The blacksmith asks for your help to find the radius of the circular arc passing through these three marked points.
铁匠请求你帮忙计算经过这三个标记点的圆弧的半径。

Concept of Relation

关系类概念

Empirical stage

经验阶段

Consider two parallel segments $x$ and $y$ (see Figure 11), each with one end on a straight line $L$ . If straight lines are drawn from the free ends of these segments (the ends not on $L$ ) to the ends on line $L$ , and if a segment $z$ parallel to $x$ and $y$ is drawn through the intersection of these two straight lines, find the relation between segments $x$ , $y$ , and $z$ .
现有两条平行线段 $x$ 与 $y$ （见图 11），每条线段各有一个端点在直线 $L$ 上。从这两条线段的自由端点（不在 $L$ 上的端点）向 $L$ 上的端点作直线，过这两条直线的交点作一条与 $x$ 、 $y$ 平行的线段 $z$ ，试找出线段 $x$ 、 $y$ 、 $z$ 之间的关系。

Figure 11. Geometric representation of relation of 𝒙, 𝒚, 𝒛 segments (Source: Authors’ own elaboration)

In a suitable digital environment, a representation can be designed to allow transformations⁶ to be performed on it, with the aim of analyzing the features under different conditions of the given situation.
在合适的数字化环境中），可设计一个可进行变换的表征，以在给定情境的不同条件下分析特征。

${}^6$ If this resource is not available, students will elaborate different representations on paper to carry out the described transformations, with the purpose of performing the corresponding analysis.
注 6：若无该资源，学生可在纸上绘制不同表征以完成下述变换与分析。

As a product of the analysis, non-essential features are identified: the length of segment $z$ does not change if the direction of $L$ changes, nor if the distance between $x$ and $y$ changes.
通过分析可识别出非本质特征：线段 $z$ 的长度不会因直线 $L$ 方向的改变而变化，也不会因线段 $x$ 与 $y$ 之间距离的改变而变化。

However, there is an essential feature: the value of $z$ changes if $x$ or $y$ changes, or if both change.
但存在一个本质特征：若 $x$ 或 $y$ 的长度改变，或两者同时改变，则 $z$ 的长度也会随之改变。

By abstraction, we can dispense with the non-essential features and emphasize the essential feature: there exists a relation in which $z$ depends only on $x$ and $y$ .
通过抽象，摒弃非本质特征，突出本质特征：存在一种关系，使得 $z$ 的取值仅依赖于 $x$ 与 $y$ 的取值。
To investigate whether this essential feature holds in other similar situations, new representations of similar situations must be created, and the necessary transformations must be performed on them to conduct this analysis.
为验证该本质特征是否在其他类似情境中成立，需构建新的类似情境表征，并对其进行必要变换以开展分析。
It is important to note that each transformation performed on the representation in the digital environment corresponds to a new similar situation; thus, it can be generalized that the abstracted essential feature can be extended to any trio of segments that satisfy the conditions of the proposed problem.
需注意的是，在数字化环境中对表征进行的每一次变换，都对应一个新的类似情境；因此可概括：抽象出的本质特征可推广到所有满足问题条件的三条线段中。
In summary, provided the parallelism conditions are satisfied, there exists a relation that establishes $z$ as a function of only $x$ and $y$ .
综上，在满足平行条件的前提下，存在一种关系使得 $z$ 仅为 $x$ 与 $y$ 的函数。

What does this relation look like? At this point, we can only describe it as a qualitative relation that establishes the dependence of $z$ on $x$ and $y$ .
这种关系具体是什么形式？目前仅能将其描述为“ $z$ 依赖于 $x$ 与 $y$ ”的定性关系。
In terms of its quantitative form, it is impossible to determine at this stage—it could involve addition, subtraction, multiplication, division, or a combination of these operations.
从定量角度来看，现阶段无法确定其具体形式——可能涉及加法、减法、乘法、除法，或这些运算的组合。
In accordance with the approach to PCF, the empirical stage cannot proceed further in this case, as it is difficult to determine the exact form of this relation. However, in the second (formalization) stage, we will be able to derive the exact form of this relation.
根据 PCF 的研究思路，经验阶段在此案例中无法进一步推进，因为难以确定该关系的具体形式。但在第二阶段（形式化阶段），我们将能够推导出该关系的精确形式。

Formalization stage

形式化阶段

At this stage, IAOT (internal actions and operations of thought) can only be supported by theoretical principles.
在本阶段，内在思维动作与操作（IAOT）仅能依靠理论原则支持。

Thus, the analysis begins with the support of Figure 12, which contains a representation of the described situation.
因此，分析将借助图 12 展开，该图呈现了上述情境的表征。

Figure 12. Representation & identification of pairs of similar triangles (Source: Authors’ own elaboration)

In this representation, it is observed that the parallelism condition between segments $x$ , $y$ , and $z$ leads to the similarity of two pairs of triangles: $\Delta 1\sim \Delta 2$ (see part a in Figure 12) and $\Delta 3\sim \Delta 4$ (see part b in Figure 12).
在该表征中，线段 $x$ 、 $y$ 、 $z$ 的平行条件使得两对三角形相似： $\Delta 1\sim \Delta 2$ （见图 12 的 a 部分）与 $\Delta 3\sim \Delta 4$ （见图 12 的 b 部分）。

The proportionality between the corresponding sides of similar triangles can be expressed as follows:
相似三角形对应边成比例，可表示为：
$$\{\begin{array}{l}\Delta 1\sim \Delta 2:\frac{n}{z}=\frac{m+n}{x}(I)\\ \Delta 3\sim \Delta 4:\frac{m}{z}=\frac{m+n}{y}(II)\end{array}$$

Adding equations (I) and (II) gives:
将等式（I）与（II）相加，可得：
$$\{\begin{array}{l}\frac{m}{z}+\frac{n}{z}=\frac{m+n}{x}+\frac{m+n}{y}\\ \frac{m+n}{z}=(m+n)\left(\frac{1}{x}+\frac{1}{y}\right)\end{array}$$
Since $m+n\ne 0$ (as they represent lengths of segments), both sides of the equation can be divided by $m+n$ , leading to:
因 $m+n\ne 0$ （ $m$ 、 $n$ 均为线段长度），等式两边可同时除以 $m+n$ ，得到：
$$\frac{1}{z}=\frac{1}{x}+\frac{1}{y}(III)$$

that is

$$\{\begin{array}{l}\frac{m}{z}+\frac{n}{z}=\frac{m+n}{x}+\frac{m+n}{y}\\ \frac{m+n}{z}=\frac{m+n}{x}+\frac{m+n}{y}\end{array}\to \frac{1}{z}=\frac{1}{x}+\frac{1}{y}\cdots (III)$$

This relation—an essential feature—can be generalized to any similar situation where the parallelism condition between the involved segments is maintained.
该关系（本质特征）可推广到所有满足“相关线段平行”条件的类似情境中。

The empirical generalization produced in the first phase of PCF only referred to the existence of a relation where one variable depends on two others; this made the mental image we formed of this relation concept somewhat vague.
PCF 第一阶段（经验阶段）产生的经验性概括，仅指出“存在一个变量依赖于另外两个变量的关系”，这使得我们对该关系类概念形成的心理意象较为模糊。

However, after the formal stage, this mental image is clarified: we now know its exact form—it is a quantitative relation, meaning that if the values of $x$ and $y$ are known, the value of $z$ can be calculated without ambiguity.
但经过形式化阶段后，该心理意象变得清晰：我们明确了其精确形式——这是一种定量关系，即已知 $x$ 与 $y$ 的取值，可无歧义地计算出 $z$ 的取值。

This is an invariant relation: it is not that the values of the involved variables do not change, but rather that the way in which they are related remains unchanged—provided that the parallelism condition between segments $x$ , $y$ , and $z$ is maintained, along with the other conditions described in the initial situation.
这是一种不变关系：并非指涉及的变量取值不变，而是指在“线段 $x$ 、 $y$ 、 $z$ 平行”及初始情境其他条件保持不变的前提下，变量之间的关联方式保持不变。

When investigating mathematical literature to determine if there is a known reference to such a relation, it was found that, by its form, the expression corresponds to $z$ being half the harmonic mean of $x$ and $y$ .
查阅数学文献后发现，该关系的形式对应“ $z$ 是 $x$ 与 $y$ 的调和平均数的一半”。

It is known that three given quantities $a$ , $b$ , $c$ are in (or form) a harmonic progression if their reciprocals are in (or form) an arithmetic progression.
已知：若三个量 $a$ 、 $b$ 、 $c$ 的倒数成等差数列，则这三个量成调和数列。

According to this definition, if $a$ , $b$ , $c$ form a harmonic progression, then $b$ is the harmonic mean of $a$ and $c$ , denoted as $b=H(a,c)$ .
据此定义，若 $a$ 、 $b$ 、 $c$ 成调和数列，则 $b$ 是 $a$ 与 $c$ 的调和平均数，记为 $b=H(a,c)$ 。

Furthermore, if $a$ , $b$ , $c$ form a harmonic progression, their reciprocals $\frac{1}{a}$ , $\frac{1}{b}$ , $\frac{1}{c}$ form an arithmetic progression, in which $\frac{1}{b}$ is the arithmetic mean of $\frac{1}{a}$ and $\frac{1}{c}$ ; that is:
此外，若 $a$ 、 $b$ 、 $c$ 成调和数列，则其倒数 $\frac{1}{a}$ 、 $\frac{1}{b}$ 、 $\frac{1}{c}$ 成等差数列，且 $\frac{1}{b}$ 是 $\frac{1}{a}$ 与 $\frac{1}{c}$ 的算术平均数，即：
$$\frac{1}{b}=A\left(\frac{1}{a},\frac{1}{c}\right)$$
Then, since the arithmetic mean of $\frac{1}{a}$ and $\frac{1}{c}$ is $\frac{\frac{1}{a}+\frac{1}{c}}{2}$ , we have:
由于 $\frac{1}{a}$ 与 $\frac{1}{c}$ 的算术平均数为 $\frac{\frac{1}{a}+\frac{1}{c}}{2}$ ，因此：
$$\frac{2}{b}=\frac{1}{a}+\frac{1}{c}(IV)$$

This final expression $(IV)$ , although derived from the formula for the arithmetic mean, identifies $b$ as the harmonic mean of $a$ and $c$ —the starting point of this analysis.
最终表达式（IV）虽源于算术平均数公式，但明确了 $b$ 是 $a$ 与 $c$ 的调和平均数，这也是本分析的起点。

Now, by comparing expressions $(III)$ and $(IV)$ , a similarity is identified; this similarity can be enhanced by performing theoretically valid operations.
对比表达式（III）与（IV），可发现两者存在相似性；通过执行理论上有效的运算，可进一步凸显这种相似性。

Thus, it is derived that $z=\frac{b}{2}(V)$ .
由此可推导出 $z=\frac{b}{2}(V)$ 。

According to this analysis, $z$ in expression $(III)$ represents half the harmonic mean of $x$ and $y$ ; this terminology will be used to refer to this expression from this point onward.
根据该分析，表达式（III）中的 $z$ 代表 $x$ 与 $y$ 的调和平均数的一半，后文将采用该术语指代该表达式。

To promote the development of the concept of “half the harmonic mean”, the following set of activities is proposed.
为推进“调和平均数的一半”这一概念的发展，设计如下系列活动。

Figure 13. Representation of half harmonic mean (Source: Authors’ own elaboration)

To begin, it is suggested to take some time to analyze part a in Figure 13, to visualize the conditions under which the relation (identifying $z$ as half the harmonic mean of $x$ and $y$ ) holds; this will facilitate answering the following questions:
首先，建议花点时间分析图 13 的 a 部分，明确“ $z$ 是 $x$ 与 $y$ 的调和平均数的一半”这一关系成立的条件，以便解答以下问题：

1. In part b of Figure 13, draw a line $L^{\prime }$ through points $Q$ and $R$ (the ends of $x$ and $y$ ); also draw a segment $w$ parallel to $x$ and $y$ passing through point $U$ . Does $w$ appear to satisfy the same conditions as $z$ ? It is obvious that it does.
   在图 13 的 b 部分，过点 $Q$ 与 $R$ （ $x$ 与 $y$ 的端点）作直线 $L^{\prime }$ ；过点 $U$ 作一条与 $x$ 、 $y$ 平行的线段 $w$ 。线段 $w$ 是否与 $z$ 满足相同条件？答案显然是肯定的。

2. What is the relation between $w$ , $x$ , and $y$ ? It is $\frac{1}{w}=\frac{1}{x}+\frac{1}{y}$ .
   线段 $w$ 与 $x$ 、 $y$ 之间的关系是什么？答案是 $\frac{1}{w}=\frac{1}{x}+\frac{1}{y}$ 。

3. Is the sum $z+w$ equivalent to segment $TV$ ? It is known that only one line parallel to a given line can pass through a point $U$ outside that line. Since segments $z$ and $w$ are both parallel to $x$ and pass through $U$ , they lie on the same line (the line parallel to $x$ passing through $U$ ); in other words, they are collinear, and their sum $z+w$ is equal to segment $TV$ .
   线段 $z+w$ 的和是否等同于线段 $TV$ ？已知过直线外一点 $U$ ，有且仅有一条直线与该直线平行。由于线段 $z$ 与 $w$ 均平行于 $x$ 且过点 $U$ ，因此它们共线（位于过 $U$ 且平行于 $x$ 的直线上），且其和 $z+w$ 等于线段 $TV$ 。

4. What does the sum $z+w$ represent? Since each of the segments $z$ and $w$ represents half the harmonic mean of $x$ and $y$ , their sum (which equals segment $TV$ ) represents the harmonic mean of $x$ and $y$ .
   线段 $z+w$ 的和代表什么？由于 $z$ 与 $w$ 均为 $x$ 与 $y$ 的调和平均数的一半，因此它们的和（即线段 $TV$ ）代表 $x$ 与 $y$ 的调和平均数。

5. Then, if segment $TV$ in part b of Figure 13 represents the harmonic mean of $x$ and $y$ , can you propose a method (using a ruler and compass) to find the harmonic mean of any two given segments $p$ and $q$ ?
   若图 13b 部分的线段 $TV$ 代表 $x$ 与 $y$ 的调和平均数，你能否提出一种方法（用直尺和圆规），以找出任意两条给定线段 $p$ 与 $q$ 的调和平均数？

   Method to find the harmonic mean of any two given quantities $p$ and $q$ (using a ruler and compass) (see Figure 14):
   用直尺和圆规求任意两个给定线段 $p$ 与 $q$ 的调和平均数的方法（见图 14）：

   
   Figure 14. Geometric representation of method for finding harmonic mean (Source: Authors’ own elaboration)

• Draw two parallel segments with lengths $p$ and $q$ , respectively, with one end of each segment on an arbitrary line $L$ .
  绘制两条长度分别为 $p$ 与 $q$ 的平行线段，每条线段各有一个端点在任意直线 $L$ 上；

• Draw a line $L^{\prime }$ through the free ends of $p$ and $q$ (the ends not on $L$ ). Additionally, draw lines connecting the ends of $p$ and $q$ to determine their intersection point $U$ .
  过 $p$ 与 $q$ 的自由端点（不在 $L$ 上的端点）作直线 $L^{\prime }$ ；同时，绘制连接 $p$ 与 $q$ 端点的直线，确定其交点 $U$ ；

• Draw a line through intersection point $U$ that is parallel to $p$ and $q$ ; let its intersections with $L$ and $L^{\prime }$ be points $T$ and $V$ , respectively.
  过交点 $U$ 作一条与 $p$ 、 $q$ 平行的直线，该直线与 $L$ 、 $L^{\prime }$ 的交点分别记为 $T$ 、 $V$ ；

• The segment $TV$ connecting these two intersection points is the harmonic mean of the given quantities $p$ and $q$ .
  连接交点 $T$ 与 $V$ 的线段 $TV$ ，即为给定线段 $p$ 与 $q$ 的调和平均数。

As a summary, the different notations used to represent the concept of the harmonic mean of two given quantities are presented below:
综上，现将“两个给定数量的调和平均数”这一概念的不同表示符号总结如下：

If $r$ , $s$ , $t$ are in (or form) a harmonic progression, then $s$ is the harmonic mean of $r$ and $t$ , denoted symbolically as $s=H(r,t)$ .
若 $r$ 、 $s$ 、 $t$ 成调和数列，则 $s$ 是 $r$ 与 $t$ 的调和平均数，符号表示为 $s=H(r,t)$ 。
This relationship can be expressed as:
其关系可表示为：
$$\frac{2}{s}=\frac{1}{r}+\frac{1}{t}(A)$$
or equivalently:
或等价表示为：
$$s=\frac{2rt}{r+t}(B)$$

6. In Figure 14, some features can be observed: quadrilateral $PQRS$ is a trapezoid (since it has parallel sides—its bases), and segment $TV$ (which we have identified as the harmonic mean of segments $PQ$ and $RS$ ) passes through the intersection of the diagonals of this trapezoid. Can you formulate or synthesize a generalization that expresses the relation between segment $TV$ and the bases of the trapezoid?
   在图 14 中可观察到以下特征：四边形 $PQRS$ 是梯形（因其有一组对边平行，即梯形的底），且线段 $TV$ （已确定为线段 $PQ$ 与 $RS$ 的调和平均数）经过该梯形对角线的交点。你能否构建并总结一个概括，以表达线段 $TV$ 与梯形两底之间的关系？

   The required generalization would take the following form:
   所需概括的形式如下：

   In any trapezoid, the segment that is parallel to the bases, passes through the intersection of the diagonals, and is bounded by the non-parallel sides (legs) is the harmonic mean of the trapezoid’s bases.
   在任意梯形中，过对角线交点且平行于两底、两端被两腰（非平行边）截取的线段，是该梯形两底的调和平均数。

7. A variation on the method for constructing the harmonic mean of two given quantities arises in the following situation: If three quantities $j$ , $k$ , $m$ are to form a harmonic progression, but only $j$ and $k$ are known, how can $m$ be determined to complete the harmonic progression?
   针对“构建两个给定数量的调和平均数”的方法，可提出如下变式问题：若需让三个数量 $j$ 、 $k$ 、 $m$ 成调和数列，但仅已知 $j$ 与 $k$ ，如何确定 $m$ 的值以完成该调和数列？

Of course, a solution can be obtained numerically using expression $(A)$ or $(B)$ . However, the interest here lies in finding a geometric solution.
当然，可通过表达式（A）或（B）以数值方式求解，但本文旨在寻找几何解法。

Considering the meaning of the generalization formulated earlier, and with the support of part a in Figure 15, the known quantities can be represented as parts of a trapezoid: $j$ is one of the bases, $k$ (as the harmonic mean) is the segment passing through the intersection of the diagonals and parallel to $j$ , and $m$ (the unknown) is the other base.
结合前文构建的概括的含义，并借助图 15 的 a 部分，可将已知数量表示为梯形的组成部分： $j$ 为梯形的一个底， $k$ （作为调和平均数）为过对角线交点且平行于 $j$ 的线段， $m$ （未知量）为梯形的另一个底。

An additional feature that emerged during the implementation of Activities 5, 6, and 7 but was not previously emphasized is that the intersection point of the diagonals is the midpoint of the segment representing the harmonic mean of the bases.
在完成活动 5、6、7 的过程中，还发现一个此前未强调的额外特征：梯形对角线的交点是“代表两底调和平均数的线段”的中点。

This feature is key to the solution, as it allows the trapezoid to be completed, as shown in part b of Figure 15, thereby determining the segment $m$ .
该特征是求解的关键——如图 15 的 b 部分所示，借助该特征可补全梯形，进而确定线段 $m$ 。

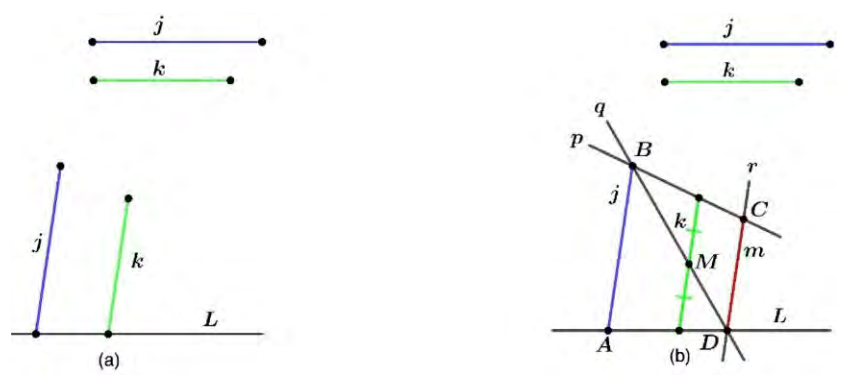
Figure 15. Alternate variation of method for finding harmonic mean (Source: Authors’ own elaboration)

The procedure required to complete the harmonic progression $j$ , $k$ , $m$ (when only $j$ and $k$ are known) consists of the following essential operations (see parts a & b in Figure 15):
当仅已知 $j$ 与 $k$ 时，完成调和数列 $j$ 、 $k$ 、 $m$ 所需的核心操作步骤如下（见图 15 的 a、b 部分）：

1. Draw segments $j\parallel k$ , with one end of each segment on an arbitrary line $L$ .
   绘制线段 $j\parallel k$ ，每条线段各有一个端点在任意直线 $L$ 上；

2. Draw a line $p$ through the free ends of $j$ and $k$ (the ends not on $L$ ). Additionally, draw a line $q$ (one of the trapezoid’s diagonals) connecting the free end of $j$ (not on $L$ ) to the midpoint $M$ of $k$ .
   过 $j$ 与 $k$ 的自由端点（不在 $L$ 上的端点）作直线 $p$ ；同时，绘制直线 $q$ （梯形的一条对角线），连接 $j$ 的自由端点（不在 $L$ 上的端点）与 $k$ 的中点 $M$ ；

3. Draw a line $r\parallel j$ through the intersection of $q$ and $L$ (i.e., $q\cap L$ ).
   过 $q$ 与 $L$ 的交点（即 $q\cap L$ ）作直线 $r\parallel j$ ；

4. The segment bounded by the intersection of $q$ and $L$ (i.e., $q\cap L$ ) and the intersection of $p$ and $r$ (i.e., $p\cap r$ ) is $m$ —the segment that completes the harmonic progression $j$ , $k$ , $m$ .
   由 $q\cap L$ 与 $p\cap r$ （ $p$ 与 $r$ 的交点）界定的线段即为 $m$ ，该线段可补全调和数列 $j$ 、 $k$ 、 $m$ 。

With this final procedure, additional terms can be added to the progression; it is only necessary to remember that, in any harmonic progression, if three consecutive terms are considered, the middle term is the harmonic mean of the other two.
借助上述步骤，可向该数列中继续添加项——只需记住：在任意调和数列中，任意三个连续项里，中间项是另外两项的调和平均数。
Figure 16 shows a representation of how the harmonic progression $d$ , $e$ , $f$ , $g$ is constructed starting from the first two terms $d$ and $e$ .
图 16 呈现了从前两项 $d$ 与 $e$ 出发，构建调和数列 $d$ 、 $e$ 、 $f$ 、 $g$ 的过程。

Figure 16. Representation of construction of harmonic progression (Source: Authors’ own elaboration)

When considering the development of the concept of “half the harmonic mean” through the application of acquired knowledge, we investigated extra-mathematical fields, particularly physical science.
在通过“应用已有知识”推进“调和平均数的一半”概念发展的过程中，我们对数学以外的领域（尤其是物理学）进行了探究。

It was found that for a circuit composed of two resistors $R_1$ and $R_2$ in parallel, the total resistance $R_T$ of the circuit is calculated using the relation:
研究发现，对于由两个电阻 $R_1$ 与 $R_2$ 组成的并联电路，电路的总电阻 $R_T$ 可通过以下关系计算：
$$\frac{1}{R_T}=\frac{1}{R_1}+\frac{1}{R_2}(\ast )$$

When compared to the expression representing half the harmonic mean of two given quantities:
将该式与“两个给定数量的调和平均数的一半”的表达式对比：
$$\frac{1}{z}=\frac{1}{x}+\frac{1}{y}(III)$$

a complete analogy between them is suggested. This analogy is achieved through abstraction: if we disregard the type of variables involved, only the magnitudes and their relational form remain consistent in both expressions. Thus, we can express: $R_T=z$ , $R_1=x$ , $R_2=y$ .
可发现两者完全类比。这种类比通过抽象实现：若忽略涉及的变量类型，仅关注数量大小及其关联形式，则两个表达式完全一致。因此，可表示为： $R_T=z$ 、 $R_1=x$ 、 $R_2=y$ 。

If we also remember that we know a method to obtain $z$ from $x$ and $y$ , then it becomes possible to solve the problem of calculating the total resistance of the parallel electrical circuit using a ruler and compass.
同时，由于我们已掌握“由 $x$ 与 $y$ 求 $z$ ”的方法，因此可通过直尺和圆规求解并联电路的总电阻。

Method: On a straight line $L$ , place the ends of two parallel scales⁷ ( $E_1\parallel E_2$ )—the direction and distance between the scales are arbitrary. Place the resistors $R_1$ and $R_2$ on scales $E_1$ and $E_2$ , respectively (see Figure 17). From this point, applying the method for constructing half the harmonic mean between $R_1$ and $R_2$ will yield $R_T$ .
方法：在直线 $L$ 上，放置两个平行刻度标尺（ $E_1\parallel E_2$ ）的端点——标尺的方向与间距可任意设定；将电阻 $R_1$ 、 $R_2$ 分别置于标尺 $E_1$ 、 $E_2$ 上（见图 17）。此后，通过“构建 $R_1$ 与 $R_2$ 的调和平均数的一半”的方法，即可得到总电阻 $R_T$ 。

⁷ These scales must be graduated in the usual units of measurement to refer to the magnitude of electrical resistances (Ω, Ohm).
注 7：这些刻度必须以常用的测量单位进行分度，以表示电阻（Ω，欧姆）的大小。

According to Figure 17, the red segment represents the magnitude of the total resistance $R_T$ ; this magnitude can be read on either scale by tracing a line parallel to $L$ (as indicated by the red arrow).
根据图 17，红色线段代表总电阻 $R_T$ 的大小；通过绘制一条平行于 $L$ 的直线（如红色箭头所示），可在任意一个标尺上读取 $R_T$ 的数值。

Figure 17. Representation of resultant in an electrical circuit & its relation to concept of half harmonic mean (Source: Authors’ own elaboration)

This problem situation could be presented in a more complex form; for example, consider an electrical circuit with more than two resistors in parallel—say four resistors $R_1$ , $R_2$ , $R_3$ , $R_4$ .
该问题情境可进一步复杂化，例如：考虑包含两个以上并联电阻的电路（如四个电阻 $R_1$ 、 $R_2$ 、 $R_3$ 、 $R_4$ ）。

Physics has shown that, in such cases, the relation between the total resistance $R_T$ and the individual resistors in the parallel circuit is given by the following expression:
物理学研究表明，在此类情况下，总电阻 $R_T$ 与各并联电阻之间的关系可通过以下表达式表示：
$$\frac{1}{R_T}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}$$

Naturally, the question arises: Can the above method be used in this case? There will be no difficulty if the following procedure is applied:
自然会产生疑问：上述方法是否可用于该情况？通过以下步骤，可顺利求解：
$$\begin{array}{rl}\frac{1}{R_T}& =\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}\\ \frac{1}{R_T}& =\frac{1}{R_{1-2}}+\frac{1}{R_3}+\frac{1}{R_4}\\ \frac{1}{R_T}& =\frac{1}{R_{1-2-3}}+\frac{1}{R_4}\\ \frac{1}{R_T}& =\frac{1}{R_{1-2-3-4}}\end{array}$$

where $R_{1-2}$ denotes the total resistance of $R_1$ and $R_2$ in parallel, $R_{1-2-3}$ denotes the total resistance of $R_{1-2}$ and $R_3$ in parallel, and $R_{1-2-3-4}$ denotes the total resistance of $R_{1-2-3}$ and $R_4$ in parallel (i.e., the total resistance $R_T$ of the four-resistor circuit).
其中， $R_{1-2}$ 表示 $R_1$ 与 $R_2$ 的并联总电阻， $R_{1-2-3}$ 表示 $R_{1-2}$ 与 $R_3$ 的并联总电阻， $R_{1-2-3-4}$ 表示 $R_{1-2-3}$ 与 $R_4$ 的并联总电阻（即四个电阻组成的电路的总电阻 $R_T$ ）。

To implement this procedure, it is suggested to sketch the circuit and perform practical operations on the representation by repeating the described method.
为执行该步骤，建议绘制电路草图，并通过重复上述方法在表征上进行实际操作。

Factors Influencing Development Of Mathematical Object Concepts: Didactic Reflections

影响数学对象概念发展的因素：教学反思

In the field of mathematics teaching, it is generally observed that, during the PCF (process of concept formation) of students, one should not expect that concepts are formed theoretically and with the highest degree of generalization in initial encounters with this task.
在数学教学领域，通常观察到：在学生的概念形成过程（PCF）中，不应期望学生在首次接触概念构建任务时，就能形成具有高度概括性的理论性概念。

This is because it depends on various factors such as educational level, prerequisite knowledge, and many others.
这是因为概念的形成依赖于多种因素，如教育阶段、先验知识等。

Instead, what usually happens in practice is that students’ concepts undergo continuous development—until their mental images reflect all the essential and common internal features of the object, as well as the highest degree of generalization that the concept deserves.
相反，实际教学中常见的情况是：学生的概念会经历持续发展，直至其心理意象能够反映对象的所有本质共性内在特征，且达到该概念应有的最高概括程度。

Four factors influence this development process: one related to the features of the object, another to the change in the category of generalization, a third to the volume of generalization, and finally, the application of knowledge in the transition from abstraction to abstraction and from abstraction to concreteness.
有四个因素会影响这一发展过程：一是与对象特征相关的因素，二是与概括类别转变相关的因素，三是与概括范围相关的因素，四是知识在“从抽象到抽象”及“从抽象到具象”过渡中的应用因素。

Features Factor

特征因素

If the mental image of an MO (mathematical object) is formed based on its external⁸ features—(1) some non-common or non-essential features, or (2) incomplete common or essential features—but through new cognitive processes, the image transitions to a state where it records complete common and essential features, we say that the concept of this MO has developed.
若某一数学对象（MO）的心理意象是基于其外在特征形成的——无论是（1）包含某些非共性或非本质特征，还是（2）仅包含不完整的共性或本质特征——但通过新的认知过程，该心理意象转变为能够反映完整共性与本质特征的状态，则表明该 MO 的概念得到了发展。

⁸ Let us designate external features, those features of MO that have been abstracted and generalized with the support of practical operations.
Similarly, theoretical features, those that have been abstracted and generalized with the support of theoretical operations.
注 8：让我们来界定外部特征，即那些在实际操作的支持下被抽象和概括出来的 MO的特征。
同样地，理论特征，即那些在理论操作的支持下被抽象和概括出来的特征。

本文中，“外在特征”指通过实际操作抽象并概括的 MO 特征；“理论特征”指通过理论操作抽象并概括的 MO 特征。

At certain levels of education, and in the specific case of the formation of the concept of the perpendicular bisector of a segment, it is very common to observe that when students are asked to perform the activities of PCF, they form a mental image that reflects the features listed in the definition that appears in many texts: Mediatrix of a given segment, is a straight line perpendicular to the segment at the midpoint; but it does not reflect all the common and essential features as it does not contemplate the essential feature, that “the mediatrix is the geometric locus of all points equidistant from the ends of the segment”. In particular, complementing his mental image with this characteristic feature represents a development for his concept of the mediatrix. In general, the search for all essential and common features is a factor in the development of the concept of MO in particular.
在某些教育阶段，特别是在线段垂直平分线概念的形成这一特定情况中，经常可以观察到：当要求学生进行 PCF 相关活动时，他们会形成一种心理表象，这种表象反映了许多教材中定义里列出的特征：给定线段的垂直平分线是一条过线段中点且与该线段垂直的直线；但它并没有反映出所有共同且本质的特征，因为它没有涵盖这样一个本质特征，即“垂直平分线是到线段两端点距离相等的所有点的几何轨迹”。特别是，用这个特征来补充其心理表象，代表着其对垂直平分线概念的一种发展。总的来说，探寻所有本质且共同的特征，尤其是 MO 概念发展的一个因素。

Change of Category of Knowledge

知识类别转变因素

In the example cited above lines, a way is described in how students can form a mental image of the mediatrix object, which registers the features of perpendicularity and passing through the midpoint of the segment, and we can even assume that they already performed the activities that allowed them to complement their mental image with the new characteristic feature, without having any proof that this is true; even if their image is correct, at this moment it corresponds to a concept of empirical character; because it is a generalization made on the basis of the external features–because they “see” that it is perpendicular, and because the equidistance is supported by practical resources, the measurements are taken with a graduated ruler or they are measured with the help of some software (GeoGebra).
知识范畴的转变：在上面所引用的例子中，描述了学生形成垂直平分线这一对象的心理表象的一种方式，这种表象记录了垂直以及过线段中点的特征，而且我们甚至可以假设，他们已经开展了一些活动，这些活动让他们能够用新的特征来补充其心理表象，尽管没有任何证据证明这是正确的；即使他们的表象是正确的，此时它也对应着一个经验性的概念；因为这是基于外部特征所做的概括——因为他们“看到”它是垂直的，而且等距性是由实际资源来支撑的，比如用刻度尺进行测量，或者借助一些软件（如 GeoGebra）来测量。

When they have gone to the internal features, essential and common to all mediatrixes–when it has been proven that it cannot be otherwise; then their concept will be developed and will have a theoretical character.
当他们深入到所有垂直平分线所共有的、本质的内部特征时——当已经证明情况必然如此时；那么他们的概念将会得到发展，并且会具有理论性。

When they progress to internal, essential, and common features of all perpendicular bisectors—when it is proven that the feature must hold (i.e., it cannot be otherwise)—their concept will develop and take on a theoretical nature.
当学生能够理解所有垂直平分线的内在、本质共性特征——即证明该特征必然成立（而非其他情况）时，他们的概念便会得到发展，并转变为理论性概念。

Generalization Volume Factor

概括范围因素

Another factor influencing the development of concepts is related to the volume of generalization of the concept.
影响概念发展的另一个因素与概念的概括范围相关。

To illustrate, consider a group of high school students who have already formed the operational concept: “method to locate a point equidistant from three given non-collinear points”.
举例来说，假设有一组高中生已形成如下操作类概念：“确定到三个不共线已知点距离相等的点的方法”。

It is clear that the volume of generalization of their concept covers any trio of non-collinear points.
显然，他们这一概念的概括范围仅涵盖“任意三个不共线点”。

However, as a teacher, you have formed this concept with a broader volume of generalization: you know that this concept can be extended to the case of any three points, even collinear ones.
但作为教师，你形成的该概念具有更广泛的概括范围：你知道该概念可推广到“任意三个点”的情况，甚至包括共线点的情况。

You know that the volume of generalization of the students’ current concept can be expanded by reducing the number of constraints—in this case, eliminating the constraint that “the three points must be non-collinear”.
你知道，可通过减少约束条件（本案例中即取消“三个点必须不共线”的约束），扩大学生当前概念的概括范围。

You also know that the method still applies in this extended case, and that the point equidistant from the three collinear points is located at infinity—specifically, it is the ideal point shared by the two perpendicular bisectors, which are parallel in this case.
你还知道，在这一扩展情况下，上述方法仍然适用，且“到三个共线点距离相等的点”位于无穷远处——具体而言，该点是两条垂直平分线（此时两条垂直平分线平行）所共有的理想点。

Thus, the volume of generalization of this concept for students can be expanded to cover any trio of points, even collinear ones.
因此，学生这一概念的概括范围可扩展到涵盖“任意三个点”，甚至包括共线点。

Now it is understood that while the students in our example may be satisfied with the volume of generalization reached in their concept formation process, the teacher knows that in order to develop their concept, by way of increasing the volume of generalization, he must necessarily work with them on some prerequisites–every ordinary straight line has a single ideal point; a family of parallels shares a single ideal point, which cannot always be covered at the educational level at which they are working. That is why we say that, in teaching, students’ concepts manifest to be in a process of development. Figure 18 shows the factors in the development of OM concepts.
现在可以理解的是，虽然我们例子中的学生可能对其概念形成过程中所达到的概括范围感到满意，但教师知道，为了发展他们的概念，通过扩大概括范围的方式，他必须和学生一起学习一些前提知识——每一条普通的直线都有一个唯一的理想点；一组平行线共享一个唯一的理想点，而这些知识在学生当前所处的教育阶段并不总是能涉及到。这就是为什么我们说，在教学中，学生的概念呈现出一种发展的过程。图 18 展示了 OM 概念发展的因素。

Figure 18. Factors in development of MO concepts (Source: Authors’ own elaboration)

Traits

• 特征
  • Incomplete traits
    不完整特征
  • Complete trits
    完整特征
  • External or no essential features
    外部或非本质特征
  • Internal or essential features
    内部或本质特征

Change in the category of knowledge

• 知识范畴的变化
  • Empirical generalizations
    经验概括
  • Theoretical generalizations
    理论概括

Volume of generalization knowledge

• 概括性知识的量
  • Lower restrictions knowledge
    低限制知识
  • Increased generalization volume knowledge
    概括量增加的知识

Application of knowledge

• 知识的应用
  • Within mathematics
    数学内部
    • From abstract
      从抽象（出发）
    • To abstract
      到抽象（应用）
  • In other disciplines
    其他学科
    • From abstract
      从抽象（出发）
    • To concrete
      到具体（应用）

Knowledge Applications Factor

知识应用因素

The application of knowledge constitutes another factor in the development of concepts, as this activity adds meaning⁹ to the knowledge constructed during PCF about an MO and, furthermore, enables the construction of new knowledge.
知识的应用是概念发展的另一个因素，因为这一活动会为 PCF 过程中构建的 MO 相关知识增添意义，此外还能为新知识的构建提供可能。

⁹ Adding meanings to the knowledge built on an MO refers, in addition to the features of the object, to several aspects, such as: the method to build it, the new knowledge generated by relating it to other MOs–the links with other concepts–, the type of problems it can solve inside and outside mathematics, among other aspects.
注 9：为基于数学对象（MO）所构建的知识赋予意义，除了涉及该对象的特征外，还包括多个方面，例如：构建该对象的方法、通过将其与其他数学对象（MO）建立联系所产生的新知识——即与其他概念的关联、以及该知识在数学内部和外部能够解决的问题类型等。

Thus, the application of knowledge about concepts such as the perpendicular bisector of a segment has generated new concepts about other MOs and corresponding solutions to practical problems, as shown in Figure 19.
因此，对“线段垂直平分线”等概念知识的应用，已产生了关于其他 MO 的新概念，并为实际问题提供了相应解决方案，如图 19 所示。

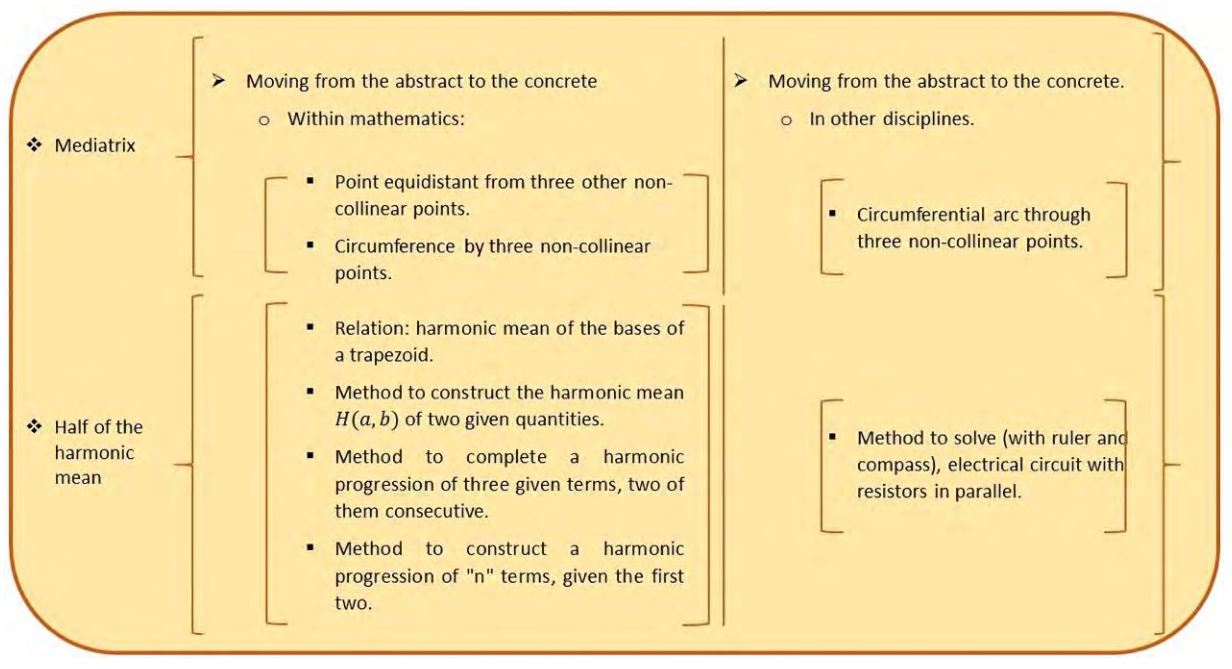
Figure 19. Concepts generated from study of mediatrix (Source: Authors’ own elaboration)

‣ Mediatrix

垂直平分线

• Moving from the abstract to the concrete
  从抽象到具体

  • Within mathematics:

    数学领域内

    • Point equidistant from three other non-collinear points.
      与另外三个不共线点等距的点。
    • Circumference by three non-collinear points.
      过三个不共线点的圆。

  • Moving from the abstract to the concrete
    从抽象到具体

  • In other disciplines:

    • Circumferential arc through three non-collinear points.
      过三个不共线点的圆弧。

‣ Half of the harmonic mean

调和平均数的一半

• Moving from the abstract to the concrete

  从抽象到具体

  • Within mathematics:
    数学领域内
    • Relation: harmonic mean of the bases of a trapezoid.
      关系：梯形两底的调和平均数。
    • Method to construct the harmonic mean $H(a,b)$ of two given quantities.
      构造两个已知量的调和平均数 $H(a,b)$ 的方法。
    • Method to complete a harmonic progression of three given terms, two of them consecutive.
      已知三个给定项（其中两个是连续的），补全调和级数的方法。
    • Method to construct a harmonic progression of “n” terms, given the first two.
      已知前两项，构造有“n”项的调和级数的方法。
  • In other disciplines:
    其他学科
    • Method to solve (with ruler and compass), electrical circuit with resistors in parallel.
      （用直尺和圆规）求解含并联电阻的电路的方法。

CONCLUSIONS

结论
To conclude, based on research on the formation and development of concepts about MOs (mathematical objects), we consider it relevant for both in-service mathematics teachers and future mathematics education professionals to reflect on the following topics:
综上，基于对数学对象（MO）概念形成与发展的研究，我们认为，在职数学教师及未来数学教育从业者有必要对以下议题进行反思：

What is the Difference Between an MO and the Concept of an MO?

数学对象（MO）与其概念的区别是什么？

On the one hand, the concept of an MO is the knowledge about that object—knowledge that humanity has been able to abstract, generalize, and synthesize after analyzing the object (or a collection of similar objects).
一方面，数学对象（MO）的概念是关于该对象的知识——这种知识是人类在对该对象（或一组类似对象）进行分析后，通过抽象、概括与综合获得的。

This knowledge takes the form of a mental image that reflects the essential features of the object.
该知识以心理意象的形式存在，能够反映对象的本质特征。

Since this image is a product of abstraction, the concept of an MO is always abstract.
由于该心理意象是抽象的产物，因此 MO 的概念始终具有抽象性。

On the other hand, an MO has no material existence.
另一方面，MO 本身并不具有物质存在形式。

To take the circle as an example: suppose a practical activity where a person drives a stake into the ground, ties a rope of arbitrary length to it, and fastens a pointed object to the other end of the rope.
以圆为例：假设有这样一项实际活动——一个人将一根木桩钉在地上，用一根任意长度的绳子将木桩与一个尖头物体连接起来。

They then move the pointed object around the stake (with the rope taut), leaving a mark of its trajectory on the ground.
随后，这个人让尖头物体绕木桩运动（保持绳子紧绷），在地面上留下运动轨迹的痕迹。

When reflecting on this special trajectory, they decide through abstraction to disregard the roughness of the ground, the width and depth of the trajectory, to assume that the trajectory is drawn on a perfectly flat surface and is so thin that it has no thickness.
在对这一特殊轨迹进行反思时，这个人通过抽象，摒弃了地面的粗糙性、轨迹的宽度与深度，假设该轨迹绘制在一个完全平整的平面上，且细到没有厚度。

They also disregard the stake and replace it with a mark so small that it has neither length nor width—a point—and disregard the elasticity of the rope to ensure that every point on the curve is equidistant from the mark (the center).
同时，这个人摒弃了木桩的实体，将其替换为一个无长度、无宽度的标记——点；并忽略绳子的弹性，以确保曲线（轨迹）上的每一点到该标记（圆心）的距离都相等。

As a product of this abstraction, a mental image is formed, which in synthesis reflects the following features of the circle as an MO: “A circle is a line containing all points equidistant from another point called the center”.
通过这一抽象过程，形成了心理意象；综合来看，该意象反映了“圆”这一 MO 的以下特征：“圆是一条包含所有到某一称为‘圆心’的点距离相等的点的线”。

However, such an object is impossible to find in concrete reality—it is clear that it can only exist on the plane of abstraction, at the conceptual level.
但这样的对象在现实中是不可能存在的——显然，它仅能存在于抽象层面，即概念层面。

Thus, we can say that an MO and its concept are identical.
因此，我们可以认为，数学对象（MO）与其概念是同一的。

Some Difficulties in Teaching Mathematical Object Concepts

数学对象概念教学中的若干难点

The adoption of the principle “to apprehend is to know” led us to seek guidance on the processes of knowledge construction.
“领会即认知”这一原则的采用，促使我们去探寻知识构建过程的规律。

The theoretical approach reviewed earlier establishes that knowledge of the objects of reality begins with sensory experience.
前文所述的理论视角认为，对现实对象的认知始于感性经验。

If we consider applying this approach to the process of knowledge acquisition in mathematics teaching, we immediately realize that MOs are not material objects—they are abstract, as they are products of abstraction.
若考虑将这一视角应用于数学教学中的知识获取过程，我们会立即意识到：MO 并非物质对象，它们是抽象的，因为它们是抽象过程的产物。

From this, we encounter a significant challenge: it is impossible to know MOs through sensory experience, i.e., we cannot have sensations, perceptions, or notions of any MO.
由此产生一个重大挑战：无法通过感性经验认知 MO，即我们无法对任何 MO 产生感觉、知觉或表象。

Therefore, knowledge of such objects is fundamentally conceptual; the use of representations is perhaps the only way to mitigate this didactic difficulty.
因此，对这类对象的认知本质上是概念性的；而表征的使用，或许是缓解这一教学难点的唯一途径。

In teaching, representations of MOs are used in an attempt to compensate for the absence of their material aspect, even though there is often a risk of confusing MOs with their representations.
教学中，人们会使用 MO 的表征来试图弥补其物质性的缺失，但这往往存在“将 MO 与其表征混淆”的风险。

Duval (1993) pointed out that this didactic difficulty—recognized by the fact that most students confuse MOs with their representations—arises from an inevitable cognitive paradox:
迪瓦尔（1993）指出，这一教学难点——表现为大多数学生将 MO 与其表征混淆——源于一个不可避免的认知悖论：

• On the one hand, in teaching, the prevailing idea is that the learning process (knowledge acquisition) of MOs is only possible through their semiotic representations. Consequently, it is quite likely that students confuse MOs with their representations, as they can only interact with the latter.
  一方面，教学中普遍认为，MO 的学习过程（知识获取）仅能通过其符号表征实现。因此，学生很可能将 MO 与其表征混淆，因为他们仅能与表征进行互动。

• On the other hand, Duval (1993) himself adds:
  另一方面，迪瓦尔（1993）本人补充道：

“This paradox is even stronger when teaching confuses mathematical activities—related to the use of procedures, algorithms, and in general the use of formal language for the acquisition of mastery of mathematical treatment—with conceptual activities, and also considers semiotic representations as secondary or extrinsic” (p. 38).
“当教学将‘与步骤、算法使用相关的数学活动（通常通过形式语言的使用来掌握数学处理方法）’与‘概念活动’混淆，且将符号表征视为次要或外在的元素时，这一悖论会更加突出”（第 38 页）。

And he concludes by stating: “Only those who have constructed the concept of an MO can recognize its different representations”.
他最后指出：“只有构建了 MO 概念的人，才能识别该 MO 的不同表征”。

How Can This Didactic Difficulty Be Avoided?

如何规避这一教学难点？

From our perspective, this didactic difficulty stems from the traditional way of conceiving mathematics teaching—i.e., the persistent promotion of the deductive approach for the knowledge acquisition process of MOs.
在我们看来，这一教学难点源于传统的数学教学理念——即始终强调采用演绎式方法进行 MO 的知识获取。

This methodological approach, which uses representations of MOs as the primary means of accessing knowledge about them, is the one most in-service teachers know and traditionally use.
这种以“MO 表征作为获取其知识的主要手段”的方法，是大多数在职教师所熟悉且传统上一直使用的方法。

This has led them to believe that this process is only possible through the use of representations, without reflecting on other possibilities.
这使得教师们认为，MO 的知识获取过程仅能通过表征实现，而不会去思考其他可能性。

Our proposal to avoid this didactic difficulty is contained in this research, where we have formulated a Didactic Perspective for the Teaching of Concepts about Mathematical Objects (DPTCMO).
本研究提出了一种规避这一教学难点的方案，即构建了“数学对象概念教学视角”（DPTCMO）。

This perspective integrates two aspects:
该视角整合了两个方面：

1. Only those who have constructed the concept of an MO can recognize its different representations (Duval, 1993).
   只有构建了 MO 概念的人，才能识别该 MO 的不同表征（迪瓦尔，1993）。

2. According to the principle “to apprehend is to know”, anyone who wishes to learn mathematics must engage in processes of mathematical knowledge construction—i.e., the PCF (process of concept formation) of MOs.
   基于“领会即认知”原则，任何想要学习数学的人，都必须参与数学知识的构建过程——即 MO 的概念形成过程（PCF）。

We exemplify its application, bearing in mind that apprehending mathematics through the inductive approach involves engaging in processes of mathematical knowledge construction.
我们通过示例展示了该视角的应用，并认为：通过归纳式方法领会数学，本质上就是参与数学知识的构建过程。

In this way, during the PCF of an MO, the learner has the opportunity to crystallize or deposit the meaning of the knowledge constructed about the object of knowledge into some form of language—i.e., into one or more forms of representation.
通过这种方式，在 MO 的 PCF 过程中，学习者有机会将“关于认知对象所构建的知识”的意义，固化或承载到某种语言形式中——即转化为一种或多种表征形式。

Such systematic and consistent knowledge construction activity serves as the factor that can prevent confusion between MOs (which exist abstractly as mental images) and their material representations.
这种系统且连贯的知识构建活动，是避免“将抽象存在的 MO（作为心理意象）与其具象表征混淆”的关键因素。

Derived from this proposal is the urgent need to be aware of the knowledge acquisition process of MOs, as this awareness is essential for teachers and future teachers to guide their students in this process.
基于这一方案，我们迫切需要了解 MO 的知识获取过程——因为这种了解对于教师及未来教师引导学生参与该过程至关重要。

As a next stage of this research, we plan to conduct experiments with a population of pre-university and university teachers.
作为本研究的下一阶段，我们计划在大学预科及大学教师群体中开展实验。

In this regard, it is acknowledged that a limitation of the present research lies in the lack of experimentation and the absence of a comparison between the theoretical-didactic elaboration and description presented here and the empirical results arising from such experimentation.
对此，我们承认：本研究的一个局限性在于缺乏实验验证，且尚未将本文提出的理论-教学阐述与描述，与实验可能产生的经验结果进行对比。

Although it is not the objective of this research to influence curriculum design, it raises the need to rethink the approaches to mathematical content promoted in schools—particularly those related to the treatment of mathematical concepts.
尽管本研究的目标并非影响课程设计，但它提出了一个需求：有必要重新思考学校中所推行的数学内容教学方法——尤其是与数学概念处理相关的方法。

Author Contributions

作者贡献

• MDC (Miguel Díaz Cárdenas): Proposed the idea of the study and wrote the core ideas.
  MDC（米格尔·迪亚斯·卡德纳斯）：提出研究思路，撰写核心观点。

• AMC (Armando Morales-Carballo): Conducted the literature review, justified the research problem, and guided the research direction.
  AMC（阿曼多·莫拉莱斯-卡瓦略）：开展文献综述，论证研究问题，指导研究方向。

• ADM (Angie Damián Mojica): Created the figures.
  ADM（安吉·达米安·莫希卡）：制作图表。

• All authors have agreed with the results and conclusions.
  所有作者均认可研究结果与结论。

Funding

资金支持

No funding source is reported for this study.
本研究无资金支持。

Ethical Statement

伦理声明

The authors stated that the research is of a theoretical-didactic nature. Therefore, an authorization process to conduct this work was not required.
作者声明，本研究属于理论-教学类研究，因此无需经过相关授权流程即可开展。

The authors adhered to the institutional ethics codes of the Organic Law of the Autonomous University of Guerrero, Mexico.
作者严格遵守墨西哥格雷罗自治大学《组织法》中规定的机构伦理准则。

Furthermore, the authors express their interest in the study of the formation and development of concepts about mathematical objects.
此外，作者对数学对象概念的形成与发展研究具有明确兴趣。

In this regard, the present work aims to provide elements for both research and the support of mathematics teachers’ teaching activities. No other goals were pursued beyond this purpose.
本研究旨在为相关研究及数学教师的教学活动提供参考要素，无其他超出该目标的意图。

Finally, the authors stated that each phase of the article evaluation process was strictly followed, which culminated successfully in the acceptance, preparation, and publication of the article.
最后，作者声明，文章评审过程的每个阶段均得到严格执行，最终顺利完成文章的接收、排版与发表。

Declaration of Interest

利益声明

No conflict of interest is declared by the authors.
作者声明无利益冲突。

Data Sharing Statement

数据共享声明

Data supporting the findings and conclusions are available upon request from the corresponding author.
支持本研究结果与结论的数据，可通过联系通讯作者获取。

REFERENCES

参考文献

Angulo, M. L., Arteaga, E., & Carmenates, O. A. (2020). La formación de conceptos matemáticos en el proceso de enseñanza-aprendizaje de la matemática [The formation of mathematical concepts in the teaching-learning process of mathematics]. Revista Conrado [Conrado Magazine], 16(74), 298-305.
安古洛､阿特加､卡门纳特斯(2020)｡《数学教与学过程中的数学概念形成》,《康拉多期刊》,第 16 卷第 74 期,第 298-305 页｡

Arteaga, E., Díaz, A., García, F., & Del Sol, J. L. (2009). Alternativas metodológicas para la formación y fijación de conceptos geométricos en la geometría plana [Methodological alternatives for the formation and fixation of geometric concepts in plane geometry]. Cuaderns Digitals [Digital Notebooks], (60), 1-25.
阿特加､迪亚斯､加西亚､德尔索尔(2009)｡《平面几何中几何概念形成与巩固的方法选择》,《数字笔记》,第 60 期,第 1-25 页｡

Ballester, S. (1992). Metodología de la enseñanza de la matemática [Mathematics teaching methodology]. Editorial Pueblo y Educación [People and Education Editorial].
巴列斯特(1992)｡《数学教学方法论》,人民与教育出版社｡

Campistrous, L. A., & Rizo, C. (2003). Sobre la estructura didáctica y metodológica de las clases [About the didactic and methodological structure of classes]. Instituto Central de Ciencias Pedagógicas de Cuba [Central Institute of Pedagogical Sciences of Cuba].
坎皮斯特罗斯､里索(2003)｡《课堂的教学与方法结构》,古巴中央教育科学研究所｡

Davýdov, V. (1982). Tipos de generalización en la enseñanza [Types of generalization in teaching]. Pueblo y Educación [People and Education].
达维多夫(1982)｡《教学中的概括类型》,人民与教育出版社｡

Duval, R. (1993). Registres de représentations sémioticiques et fonctionnement cognitif de la pensée [Registers of semiotic representations and cognitive functioning of thought]. Annales de Didactique et de Science Cognitives [Annals of Didactics and Cognitive Science], 1(5), 37-65.
迪瓦尔(1993)｡《符号表征形式与思维的认知功能》,《教学与认知科学年鉴》,第 1 卷第 5 期,第 37-65 页｡

Guétmanova, A. (1989). Lógica: Serie biblioteca del estudiante [Logic: Student library series]. Progreso.
格特曼诺娃(1989)｡《逻辑学:学生文库系列》,普罗格 reso 出版社｡

Hernández-Gómez, J. C., Locia-Espinoza, E., Morales-Carballo, A., & Sigarreta-Almira, J. M. (2019). El contraejemplo en la elaboración de la definición de función convexa por estudiantes universitarios [The counterexample in the elaboration of the definition of a convex function by university students]. Información Tecnológica [Technological Information], 30(1), 185-202. https://doi.org/10.4067/S0718-07642019000100185
埃尔南德斯-戈麦斯､洛西亚-埃斯皮诺萨､莫拉莱斯-卡瓦略､西加雷塔-阿尔米拉(2019)｡《大学生构建凸函数定义过程中的反例应用》,《科技信息》,第 30 卷第 1 期,第 185-202 页｡https://doi.org/10.4067/S0718-07642019000100185

Jungk, W. (1985). Metodología de la enseñanza de la matemática [Mathematics teaching methodology]. Pueblo y Educación [People and Education].
荣克(1985)｡《数学教学方法论》,人民与教育出版社｡

Leontiev, A. N. (1981). Actividad, conciencia, personalidad [Activity, consciousness, personality]. Pueblo y Educación [People and Education].
列昂节夫(1981)｡《活动､意识与人格》,人民与教育出版社｡

Locia, E., Mederos, O. B., Sigarreta, J. M., & Villarraga, B. (2018). Aproximación teórico-metodológica a la formación de conceptos matemáticos [Theoretical-methodological approach to the formation of mathematical concepts]. Premisa [Premise], 20(29), 24-38.
洛西亚､梅德罗斯､西加雷塔､比利亚拉加(2018)｡《数学概念形成的理论-方法视角》,《前提》,第 20 卷第 29 期,第 24-38 页｡

Majmutov, M. (1983). La enseñanza problémica [The problematic teaching]. Pueblo y Educación [People and Education].
马吉穆托夫(1983)｡《问题式教学》,人民与教育出版社｡

Morales, A., & Damián, A. (2021a). Errores y dificultades acerca de las rectas notables del triángulo. Etapa preliminar para la elaboración de trayectorias de aprendizaje [Errors and difficulties about the notable lines of the triangle. Preliminary stage for the development of learning trajectories]. UNIÓN: Revista Iberoamericana de Educación Matemática [UNION: Ibero-American Magazine of Mathematics Education], 61, 1-17.
莫拉莱斯､达米安(2021a)｡《三角形特殊线的常见错误与难点:学习路径构建的初步阶段》,《联盟:伊比利亚美洲数学教育期刊》,第 61 期,第 1-17 页｡

Morales, A., & Damián, A. (2021b). Estrategia didáctica fundamentada en el uso de GeoGebra para mejorar la comprensión del concepto de semejanza de triángulos [Teaching strategy based on the use of GeoGebra to improve understanding of the concept of similarity of triangles]. Innovación Educativa [Educational Innovation], 21(18), 11-34.
莫拉莱斯､达米安(2021b)｡《基于 GeoGebra 的教学策略:提升三角形相似概念的理解》,《教育创新》,第 21 卷第 18 期,第 11-34 页｡

Morales-Carballo, A., Damián Mojica, A., & Marmolejo Vega, J. E. (2022). Hypothetical learning trajectory for assimilating the articulated concepts of quadratic function and equation through variational ideas and the use of GeoGebra in pre-university students. International Electronic Journal of Mathematics Education, 17(2), em0678. https://doi.org/10.29333/iejme/11714
莫拉莱斯-卡瓦略､达米安·莫希卡､马尔莫莱霍·维加(2022)｡《借助变分思想与 GeoGebra,帮助大学预科生内化二次函数与二次方程关联概念的假设性学习路径》,《国际数学教育电子期刊》,第 17 卷第 2 期,文章编号 em0678｡https://doi.org/10.29333/iejme/11714

Ramos, G., & López, A. (2015). La formación de conceptos: una comparación entre los enfoques cognitivista e histórico-cultural [The formation of concepts: a comparison between cognitivist and historical-cultural approaches]. Educação e Pesquisa [Education and Research], 41(3), 615-628. https://doi.org/10.1590/S1517-9702201507135042
拉莫斯､洛佩斯(2015)｡《概念形成:认知主义与历史文化主义视角的对比》,《教育与研究》,第 41 卷第 3 期,第 615-628 页｡https://doi.org/10.1590/S1517-9702201507135042

Rizo, C., & Campistrous, L. (2011). Algunas implicaciones de la filosofía Marxista para la enseñanza de la matemática: El caso de Cuba [Some implications of Marxist philosophy for the teaching of mathematics: The case of Cuba]. Revista Iberoamericana de Educación [Ibero-American Journal of Education], 56, 179-199. https://doi.org/10.35362/rie560516
里索､坎皮斯特罗斯(2011)｡《马克思主义哲学对数学教学的若干启示:以古巴为例》,《伊比利亚美洲教育期刊》,第 56 期,第 179-199 页｡https://doi.org/10.35362/rie560516

Rubinstein, S. L. (1969). Principios de psicología general [Principles of general psychology]. Edición Revolucionaria [Revolutionary Edition].
鲁宾斯坦(1969)｡《普通心理学原理》,革命出版社｡

Sierpinska, A. (1987). Humanities students and epistemological obstacles related to limits. Educational Studies in Mathematics, 18, 371-397. https://doi.org/10.1007/BF00240986
希耶平斯卡(1987)｡《文科学生与极限相关的认知障碍》,《数学教育研究》,第 18 卷,第 371-397 页｡https://doi.org/10.1007/BF00240986

Tall, D. (1991). The psychology of advanced mathematical thinking. In D. Tall (Ed.), Advanced mathematical thinking (pp. 3-21). Kluwer. https://doi.org/10.1007/0-306-47203-1
托尔(1991)｡《高等数学思维心理学》,收录于 D.托尔(编)《高等数学思维》(第 3-21 页),克卢弗出版社｡https://doi.org/10.1007/0-306-47203-1

Vinner, S. (1991). The role of definitions in the teaching and learning of mathematics. In D. Tall (Ed.), Advanced mathematical thinking (pp. 65-81). Kluwer. https://doi.org/10.1007/0-306-47203-1_5
文纳(1991)｡《定义在数学教与学中的作用》,收录于 D.托尔(编)《高等数学思维》(第 65-81 页),克卢弗出版社｡https://doi.org/10.1007/0-306-47203-1_5

Winicki-Landman, G. (2006). Las definiciones en matemáticas y los procesos de su formulación: Algunas reflexiones [Definitions in mathematics and the processes of their formulation: Some reflections]. Acta Latinoamericana de Matemática Educativa [Latin American Journal of Research in Mathematics Education], 19, 528-537.
维尼奇-兰德曼(2006)｡《数学中的定义及其构建过程:若干反思》,《拉丁美洲数学教育学报》,第 19 卷,第 528-537 页｡

---

via：

• Formation and development of mathematical concepts: Elements for research and teaching
  https://files.eric.ed.gov/fulltext/EJ1417386.pdf

• 丘成桐：数学史大纲（Brief History of Math）
  https://yauc.seu.edu.cn/2020/0820/c27551a342885/page.htm

• 数学概念之源 (豆瓣)
  https://book.douban.com/subject/35893392/