微积分 | 如何学好微积分

斐夷所非

已于 2025-07-25 06:51:36 修改

阅读量497

点赞数 4

CC 4.0 BY-SA版权

分类专栏： mathematics 文章标签：微积分学习

于 2025-07-25 01:27:00 首次发布

本文链接：https://blog.youkuaiyun.com/u013669912/article/details/149614039

mathematics 专栏收录该内容

75 篇文章

订阅专栏

注：本文为 “微积分学习” 相关合辑。
英文引文，机翻未校。
中文引文，略作重排。
图片清晰度受引文原图所限。
如有内容异常，请看原文。

A Gentle Introduction To Learning Calculus

微积分学习入门：温和引导

I have a love/hate relationship with calculus: it demonstrates the beauty of math and the agony of math education.
我与微积分有着爱恨交织的关系：它既展现了数学之美，也暴露了数学教育之痛。

Calculus relates topics in an elegant, brain-bending manner. My closest analogy is Darwin’s Theory of Evolution: once understood, you start seeing Nature in terms of survival. You understand why drugs lead to resistant germs (survival of the fittest). You know why sugar and fat taste sweet (encourage consumption of high-calorie foods in times of scarcity). It all fits together.
微积分以一种优雅又令人烧脑的方式将各个知识点联系起来。我能想到的最贴切类比是达尔文的进化论：一旦理解，你就会开始从生存的角度看待自然界。你会明白为什么药物会导致病菌产生抗药性（适者生存）；你会知道为什么糖和脂肪尝起来是甜的（在食物匮乏时，鼓励人们摄入高热量食物）。一切都能说得通。

Calculus is similarly enlightening. Don’t these formulas seem related in some way?
微积分同样具有启发意义。这些公式难道不像是以某种方式相互关联的吗？

Circle and Sphere Fun Facts

圆与球的趣味知识

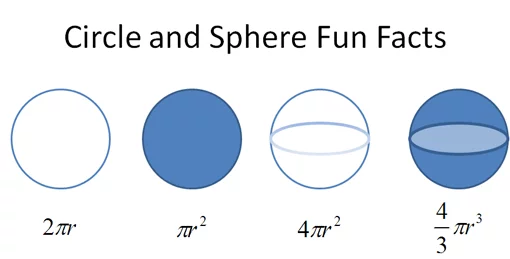
在这里插入图片描述

They are. But most of us learn these formulas independently. Calculus lets us start with circumference = 2π r and figure out the others — the Greeks would have appreciated this.
它们确实是相关的。但我们大多数人都是孤立地学习这些公式。借助微积分，我们可以从圆的周长 = 2πr 出发，推导出其他公式 —— 古希腊人要是知道了，一定会赞叹不已。

Unfortunately, calculus can epitomize what’s wrong with math education. Most lessons feature contrived examples, arcane proofs, and memorization that body slam our intuition & enthusiasm.
遗憾的是，微积分堪称数学教育问题的缩影。大多数课程充斥着刻意编造的例子、晦涩难懂的证明和死记硬背，这些都狠狠打击了我们的直觉和热情。

It really shouldn’t be this way.
事情真的不该是这样的。

Math, art, and ideas

数学、艺术与思想

I’ve learned something from school: Math isn’t the hard part of math; motivation is. Specifically, staying encouraged despite
我从学校里悟到了一点：数学本身并非数学学习中最难的部分，难的是动力。具体来说，是在种种情况下依然保持热情：

Teachers focused more on publishing/perishing than teaching
教师更关注 “要么发表要么消亡”（学术压力），而非教学
Self-fulfilling prophecies that math is difficult, boring, unpopular or “not your subject”
认为数学难、枯燥、冷门或 “不是你该学的学科” 这种自我应验的预言
Textbooks and curriculums more concerned with profits and test results than insight
教材和课程更在意利润和考试成绩，而非启发思考

‘A Mathematician’s Lament’ is an excellent essay on this issue that resonated with many people:
《一位数学家的哀叹》是一篇关于这个问题的精彩文章，引起了很多人的共鸣：

“…if I had to design a mechanism for the express purpose of destroying a child’s natural curiosity and love of pattern-making, I couldn’t possibly do as good a job as is currently being done — I simply wouldn’t have the imagination to come up with the kind of senseless, soul-crushing ideas that constitute contemporary mathematics education.”
“…… 如果我必须设计一个机制，其明确目的是摧毁孩子天生的好奇心和对模式构建的热爱，我绝不可能做得像现在这样好 —— 我根本想不出那种毫无意义、摧残心灵的想法，而这些想法正是当代数学教育的组成部分。”

Microsoft Word - LockhartsLament.doc - Lockhart_2002_-_A_Mathematician’s_Lament.pdf
https://worrydream.com/refs/Lockhart_2002_-_A_Mathematician’s_Lament.pdf
A Mathematician’s Lament - Reviewed by William Schmidt
https://www.ams.org/notices/201304/rnoti-p461.pdf

Imagine teaching art like this: Kids, no fingerpainting in kindergarten. Instead, let’s study paint chemistry, the physics of light, and the anatomy of the eye. After 12 years of this, if the kids (now teenagers) don’t hate art already, they may begin to start coloring on their own. After all, they have the “rigorous, testable” fundamentals to start appreciating art. Right?
试想一下，如果艺术课也这么教：孩子们，幼儿园不准玩指画。相反，我们来学习颜料化学、光的物理原理以及眼睛的解剖结构。这样学 12 年后，如果这些孩子（现在已是青少年）还没讨厌艺术，他们或许会开始自己涂色。毕竟，他们已经掌握了 “严谨的、可检验的” 基础知识，可以开始欣赏艺术了。对吧？

Poetry is similar. Imagine studying this quote (formula):
诗歌也是如此。试想一下，如果这样学习这句引语（公式）：

This above all: to thine own self be true,
And it must follow, as the night the day,
Thou canst not then be false to any man.

— William Shakespeare, Hamlet

最要紧的是，你必须对自己忠实；
正像有了白昼才有黑夜一样，
对自己忠实，才不会对别人欺诈。

—— 威廉・莎士比亚，《哈姆雷特》

It’s an elegant way of saying “be yourself” (and if that means writing irreverently about math, so be it). But if this were math class, we’d be counting the syllables, analyzing the iambic pentameter, and mapping out the subject, verb and object.
这句话用优雅的方式表达了 “做自己”（如果这意味着可以不拘礼节地谈论数学，那也无妨）。但如果这是数学课，我们会去数音节、分析抑扬格五音步，还要划分主语、谓语和宾语。

Math and poetry are fingers pointing at the moon. Don’t confuse the finger for the moon. Formulas are a means to an end, a way to express a mathematical truth.
数学和诗歌都像是指向月亮的手指。不要把手指当成月亮。公式是达到目的的手段，是表达数学真理的一种方式。

We’ve forgotten that math is about ideas, not robotically manipulating the formulas that express them.
我们忘了，数学关乎思想，而非机械地摆弄那些表达思想的公式。

Ok bub, what’s your great idea?

好了，伙计，你的高见是什么？

Feisty, are we? Well, here’s what I won’t do: recreate the existing textbooks. If you need answers right away for that big test, there’s plenty of websites, class videos and 20-minute sprints to help you out.
我们是不是有点急躁了？好吧，我不会做的是：重蹈现有教材的覆辙。如果你急需答案应付重要考试，有很多网站、课堂视频和 20 分钟速成内容可以帮你。

Instead, let’s share the core insights of calculus. Equations aren’t enough — I want the “aha!” moments that make everything click.
相反，让我们来分享微积分的核心洞见。光有方程是不够的 —— 我想要的是那种 “啊哈！” 的瞬间，让一切豁然开朗。

Formal mathematical language is one just one way to communicate. Diagrams, animations, and just plain talkin’ can often provide more insight than a page full of proofs.
正式的数学语言只是一种交流方式。图表、动画，还有简单直白的讲解，往往比一整页的证明更能带来启发。

But calculus is hard!

但微积分很难啊！

I think anyone can appreciate the core ideas of calculus. We don’t need to be writers to enjoy Shakespeare.
我认为任何人都能理解微积分的核心思想。我们不必成为作家才能欣赏莎士比亚。

It’s within your reach if you know algebra and have a general interest in math. Not long ago, reading and writing were the work of trained scribes. Yet today that can be handled by a 10-year old. Why?
只要你懂代数，对数学有大致兴趣，微积分就触手可及。不久前，读写还是受过训练的抄写员的工作。但如今，一个 10 岁的孩子就能做到。为什么呢？

Because we expect it. Expectations play a huge part in what’s possible. So expect that calculus is just another subject. Some people get into the nitty-gritty (the writers/mathematicians). But the rest of us can still admire what’s happening, and expand our brain along the way.
因为我们对孩子有这样的期待。期待在可能性中扮演着重要角色。所以，把微积分当成另一门学科就好。有些人会深入钻研细节（比如数学家和相关作者）。但我们其他人仍然可以去理解其中的道理，在此过程中拓展思维。

It’s about how far you want to go. I’d love for everyone to understand the core concepts of calculus and say “whoa”.
这取决于你想深入到什么程度。我希望每个人都能理解微积分的核心概念，然后惊叹一声 “哇”。

So what’s calculus about?

那么，微积分到底是什么？

Some define calculus as “the branch of mathematics that deals with limits and the differentiation and integration of functions of one or more variables”. It’s correct, but not helpful for beginners.
有人将微积分定义为 “研究极限以及单变量或多变量函数的微分和积分的数学分支”。这是正确的，但对初学者没什么帮助。

Here’s my take: Calculus does to algebra what algebra did to arithmetic.
我的理解是：微积分之于代数，正如代数之于算术。

Arithmetic is about manipulating numbers (addition, multiplication, etc.).

算术是关于数字运算的（加法、乘法等）。
Algebra finds patterns between numbers: a² + b² = c² is a famous relationship, describing the sides of a right triangle. Algebra finds entire sets of numbers — if you know a and b, you can find c.

代数寻找数字之间的模式：a² + b² = c² 是一个著名的关系式，描述了直角三角形的边长关系。代数能找到一整套数字 —— 如果你知道 a 和 b，就能求出 c。
Calculus finds patterns between equations: you can see how one equation (circumference = 2π r ) relates to a similar one ( area = πr² ).

微积分寻找方程之间的模式：你能发现一个方程（周长 = 2πr）与另一个类似方程（面积 =πr²）之间的关联。

Using calculus, we can ask all sorts of questions:
借助微积分，我们可以提出各种各样的问题：

How does an equation grow and shrink? Accumulate over time?

一个方程如何增长和衰减？如何随时间累积？
When does it reach its highest/lowest point?

它在何时达到最高点 / 最低点？
How do we use variables that are constantly changing? (Heat, motion, populations, …).

我们如何处理不断变化的变量？（热量、运动、人口等）。
And much, much more!

还有更多、更多的问题！

Algebra & calculus are a problem-solving duo: calculus finds new equations, and algebra solves them. Like evolution, calculus expands your understanding of how Nature works.
代数和微积分是解决问题的黄金搭档：微积分发现新方程，代数求解这些方程。就像进化论一样，微积分能拓宽你对自然界运行方式的理解。

An Example, Please

请举个例子

Let’s walk the walk. Suppose we know the equation for circumference ( 2 πr ) and want to find area. What to do?
让我们付诸实践。假设我们知道周长的方程（2πr），想求出面积。该怎么做呢？

Realize that a filled-in disc is like a set of Russian dolls.
要明白，一个实心圆盘就像一套俄罗斯套娃。

Dissecting a Circle

剖析圆

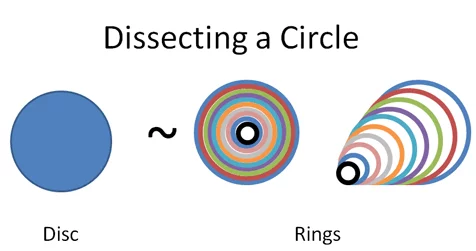
在这里插入图片描述

Disc Rings
圆盘圆环

Here are two ways to draw a disc:
画圆盘有两种方法：

Make a circle and fill it in
画一个圆，然后涂满它
Draw a bunch of rings with a thick marker
用粗马克笔绘制一堆圆环

The amount of “space” (area) should be the same in each case, right? And how much space does a ring use?
两种情况下的 “空间”（面积）应该是一样的，对吧？那么一个圆环占用多少空间呢？

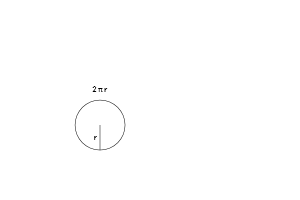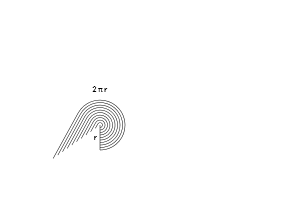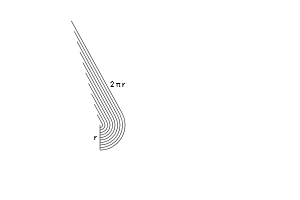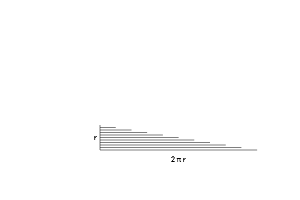
Well, the very largest ring has radius “r” and a circumference 2 πr . As the rings get smaller their circumference shrinks, but it keeps the pattern of 2 π ⋅ current radius . The final ring is more like a pinpoint, with no circumference at all.
最大的圆环半径为 “r”，周长为 2πr。随着圆环变小，其周长也会缩短，但始终遵循 “2π× 当前半径” 的规律。最后一个圆环更像一个点，根本没有周长。

Unroll the Rings

展开圆环

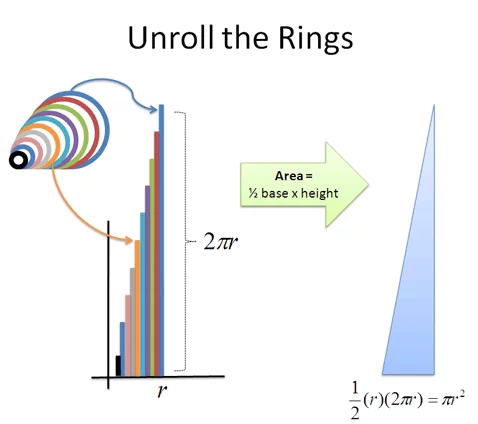
在这里插入图片描述

Now here’s where things get funky. Let’s unroll those rings and line them up. What happens?
现在有趣的地方来了。让我们把这些圆环展开并排列起来。会发生什么呢？

We get a bunch of lines, making a jagged triangle. But if we take thinner rings, that triangle becomes less jagged (more on this in future articles).
我们会得到一堆线段，组成一个锯齿状的三角形。但如果我们取更细的圆环，这个三角形的锯齿会变少（后续文章会详细介绍）。

One side has the smallest ring (0) and the other side has the largest ring ( 2 πr )
一边是最小的圆环（0），另一边是最大的圆环（2πr）

We have rings going from radius 0 to up to “r”. For each possible radius (0 to r), we just place the unrolled ring at that location.
我们的圆环半径从 0 一直到 “r”。对于每个可能的半径（0 到 r），我们只需将展开的圆环放在相应的位置。

The total area of the “ring triangle” = 1/2 base ⋅ height = 1/2 ( r) ( 2 πr) = π r² , which is the formula for area!
这个 “圆环三角形” 的总面积 = 1/2× 底 × 高 = 1/2×r×(2πr) = πr²，这正是圆的面积公式！

Yowza! The combined area of the rings = the area of the triangle = area of circle!
哇哦！所有圆环的总面积 = 三角形的面积 = 圆的面积！

(Image from Wikipedia)
（图片来自维基百科）

This was a quick example, but did you catch the key idea? We took a disc, split it up, and put the segments together in a different way. Calculus showed us that a disc and ring are intimately related: a disc is really just a bunch of rings.
这是一个简单的例子，但你抓住核心思想了吗？我们把一个圆盘拆开，再以不同的方式重新组合这些部分。微积分向我们展示了圆盘和圆环的密切关系：圆盘其实就是一堆圆环的组合。

This is a recurring theme in calculus: Big things are made from little things. And sometimes the little things are easier to work with.
这是微积分中一个反复出现的主题：大的事物由小的部分组成。而且有时候，小的部分更容易处理。

A note on examples

关于例子的说明

Many calculus examples are based on physics. That’s great, but it can be hard to relate: honestly, how often do you know the equation for velocity for an object? Less than once a week, if that.
很多微积分例子都以物理为基础。这很好，但可能难以产生共鸣：说实话，你多久会用到一次物体的速度方程？就算有，一周也不到一次吧。

I prefer starting with physical, visual examples because it’s how our minds work. That ring/circle thing we made? You could build it out of several pipe cleaners, separate them, and straighten them into a crude triangle to see if the math really works. That’s just not happening with your velocity equation.
我更喜欢从具体可见的例子入手，因为这符合我们的思维方式。我们刚才做的圆环 / 圆的例子？你可以用几根扭扭棒做出来，把它们分开，再拉直成一个粗糙的三角形，看看这个数学原理是否真的成立。但速度方程就做不到这一点。

A note on rigor (for the math geeks)

关于严谨性（给数学爱好者的说明）

I can feel the math pedants firing up their keyboards. Just a few words on “rigor”.
我能感觉到数学学究们已经准备好敲击键盘反驳了。关于 “严谨性”，我简单说几句。

Did you know we don’t learn calculus the way Newton and Leibniz discovered it? They used intuitive ideas of “fluxions” and “infinitesimals” which were replaced with limits because “Sure, it works in practice. But does it work in theory?”.
你知道吗？我们学习微积分的方式并非牛顿和莱布尼茨发现它的方式。他们使用的是 “流数” 和 “无穷小” 的直观概念，后来这些概念被极限取代，只因 “当然，它在实践中是有效的。但在理论上也有效吗？”

We’ve created complex mechanical constructs to “rigorously” prove calculus, but have lost our intuition in the process.
我们构建了复杂的机械性结构来 “严谨地” 证明微积分，却在这个过程中丢失了直觉。

We’re looking at the sweetness of sugar from the level of brain-chemistry, instead of recognizing it as Nature’s way of saying “This has lots of energy. Eat it.”
我们从大脑化学的层面去研究糖的甜味，却没有意识到这是大自然在说 “这东西能量很高，快吃吧”。

I don’t want to (and can’t) teach an analysis course or train researchers. Would it be so bad if everyone understood calculus to the “non-rigorous” level that Newton did? That it changed how they saw the world, as it did for him?
我不想（也不能）教授分析课程或培养研究人员。如果每个人都能以牛顿那种 “非严谨” 的程度理解微积分 —— 就像微积分改变了牛顿看待世界的方式一样，也改变他们看待世界的方式 —— 那会很糟糕吗？

A premature focus on rigor dissuades students and makes math hard to learn. Case in point: e is technically defined by a limit, but the intuition of growth is how it was discovered. The natural log can be seen as an integral, or the time needed to grow. Which explanations help beginners more?
过早强调严谨性会让学生却步，使数学难以学习。举个例子：从技术上讲，e 的定义涉及极限，但它的发现源于对增长的直观理解。自然对数可以被视为积分，也可以被视为增长所需的时间。哪种解释对初学者更有帮助呢？

Let’s fingerpaint a bit, and get into the chemistry along the way. Happy math.
让我们先玩玩 “指画”，再慢慢深入 “化学”（比喻先直观感受再深入理论）。祝大家享受数学的乐趣。

10 Tips On Learning Calculus

10个学习微积分的技巧

Here are the best ways to learn calculus and ace your tests:
以下是学习微积分并在考试中取得好成绩的最佳方法：

1- Understand The Basics

1- 理解基础知识

First, what is calculus? Calculus is defined as the branch of mathematics that studies rates of change. It provides a framework for modeling techniques involving change and a way to extrapolate predictions of such models (Source: Massachusetts Institute of Technology)
首先，什么是微积分？微积分被定义为研究变化率的数学分支。它为涉及变化的建模技术提供了一个框架，并为这类模型的预测推断提供了方法（来源：麻省理工学院）

There are two kinds of calculus:
微积分有两种：

Differential calculus defines the rate of change of a quantity.
微分学定义了一个量的变化率。
Integral calculus studies the quantity where the rate of change is generally known.
积分学研究变化率已知的量。

You can plan to ace any subject, but the efforts will be futile if your basic understanding is lacking. Calculus can be connected to other branches of math to offer you challenging questions. So your other concepts must be clear to solve the problem.
你可以制定在任何学科取得好成绩的计划，但如果缺乏对基础知识的理解，所有努力都将是徒劳的。微积分会与其他数学分支相联系，从而产生具有挑战性的问题。因此，要解决这些问题，你必须清楚其他相关概念。

Arithmetic is an important part of this branch of math, so the different operations must be at your fingertips.
算术是这一数学分支的重要组成部分，所以你必须熟练掌握各种运算。
Algebra may also form a major part of your calculus problems. You must have adequate knowledge of different properties and sets.
代数也可能在你的微积分问题中占很大比重。你必须充分了解各种性质和集合。
Trigonometric concepts are easier to understand and ace. So you should understand the various properties of shapes, such as triangles and circles.
三角学概念相对容易理解和掌握。所以你应该了解各种图形的性质，比如三角形和圆形。
The last field that you must be aware of is geometry. Studying all the shapes relevant to mathematics and their properties will allow you to solve various questions easily.
最后一个你必须了解的领域是几何学。学习所有与数学相关的图形及其性质，会让你轻松解决各种问题。

2- Learn The Different Aspects Of Calculus

2- 了解微积分的不同方面

Calculus may seem like a single subject to you, but it has been divided into two major parts. All students are expected to master differential and integral calculus to pass their tests.
在你看来，微积分可能像是一门单一的学科，但它其实分为两个主要部分。所有学生要通过考试，都需要掌握微分学和积分学。

You will have to learn about the rate of change, which means that you should have knowledge of accumulation and derivatives. Rate is also essential to calculus, so you will have to work on different relations.
你需要学习变化率，这意味着你要了解累积和导数的知识。速率对微积分也很关键，所以你要研究不同的关系。

These include time vs. velocity, rate of change vs. distance, and more. Understanding these concepts is necessary for solving graphic questions.
这些关系包括时间与速度、变化率与距离等等。理解这些概念是解决图形问题的必要条件。

3- Often Review Your Formulae

3- 经常复习公式

The concepts of calculus have various basic formulae to help solve questions. So you must learn them before starting to practice different problems. These basic formulae will help you at multiple stages of calculus.
微积分的概念包含各种基本公式，有助于解决问题。所以在开始练习不同的题目之前，你必须学会这些公式。这些基本公式会在微积分学习的多个阶段对你有所帮助。

This is why you should not think of skipping them. The best way to learn the formulae is by understanding their derivations. This is a better approach than memorizing the final formula because you will have to learn many of them.
这就是为什么你不应该想着跳过它们。学习公式的最佳方法是理解它们的推导过程。这比死记硬背最终的公式要好，因为你需要学习的公式有很多。

The best part about understanding the derivations is that it will allow you to derive a specific formula during the test. So you will not have to worry about failing to remember the final equation.
理解推导过程的最大好处是，在考试时你可以推导出特定的公式。这样你就不用担心记不住最终的等式了。

4- Do Not Skip Classes

4- 不要逃课

Another best way to learn calculus is to avoid skipping classes. This subject is tough and requires a good understanding of different concepts. If you skip even one class, you may fall behind and fail to understand the following topics.
学习微积分的另一个好方法是不要逃课。这门学科很难，需要对各种概念有很好的理解。即使你逃了一节课，也可能会落后，并且无法理解接下来的内容。

So attending classes is necessary to ensure you have a basic understanding of each calculus concept. Then, you can practice the topic at home to memorize and retain the new knowledge.
所以上课是必要的，以确保你对每个微积分概念都有基本的理解。然后，你可以在家练习这个主题，以记住并巩固新知识。

You must also remember that classes will help you learn easy problem-solving techniques that may not be present in books. Spending two to four hours on homework assignments is also best.
你还必须记住，上课能帮助你学到书本上可能没有的简便解题技巧。花两到四个小时做家庭作业也是最好的。

5- Avoid Falling Behind

5- 避免落后

If you fall behind in calculus, it will be difficult to catch up because of the tough concepts. You may have to skip classes due to personal issues, but that does not mean you should be laid back when it comes to studying.
在微积分学习中，如果你落后了，由于概念难懂，将很难赶上。你可能因为个人原因不得不逃课，但这并不意味着你在学习上可以松懈。

You can form a study group with students with clear concepts. A three to five students group is best for understanding calculus. Meeting daily can help you stay up to date with the class schedule.
你可以和概念清晰的学生组成学习小组。3到5人的小组最适合学习微积分。每天见面可以帮助你跟上课程进度。

If you cannot work with a study group, you should use multiple online resources to grasp the newly taught topics.
如果你不能参加学习小组，你应该利用多种在线资源来掌握新教的内容。

Khan Academy is a great platform for learning calculus. You may also watch lectures on YouTube by well-reputed teachers.
可汗学院是学习微积分的好平台。你也可以观看 YouTube 上知名教师的讲座。

6- Learn About Limits And Fundamental Theorem

6- 学习极限和基本定理

Limits and fundamental theorem in calculus are important concepts in which you must be well-versed. When solving a complex function, you can use limits to break it down into easy fragments.
微积分中的极限和基本定理是你必须精通的重要概念。在解决复杂函数时，你可以用极限将其分解为简单的部分。

You can solve these small parts and add them to get the final answer. The fundamental theorem allows you to understand that integration and differentiation are inverse to each other .
你可以解决这些小部分，然后把它们加起来得到最终答案。基本定理让你明白积分和微分是互逆的运算。

Being aware of this concept will allow you to understand the two parts of calculus. You should also note that skipping the theorem is impossible when doing this subject.
了解这个概念会让你理解微积分的两个部分。你还应该注意，学习这门学科时，跳过定理是不可能的。

7- Practice Problems

7- 练习题目

Math is a subject that requires high skills and a lot of practice regardless of the branch you are doing. You may understand derivations and memorize the formulae, but that will be useless if you don’t practice question s.
无论你学习的是哪个数学分支，数学都需要高超的技能和大量的练习。你可能理解推导过程，也记住了公式，但如果不练习题目，这些都将毫无用处。

Thinking that understanding concepts will be enough to perform well in exams is ill-advised. You must practice different problems to know the areas you are well-prepared for and the parts where you are lacking.
认为只要理解概念就能在考试中取得好成绩是不明智的。你必须练习不同的题目，才能知道自己哪些方面准备充分，哪些方面还有不足。

As a beginner, you should with questions related to derivatives and gradually move towards integral problems. It is best to answer as many questions as possible within a day. Regular practice will help you nail your tests and exams easily.
作为初学者，你应该从与导数相关的题目开始，逐渐过渡到积分问题。最好一天内尽可能多地答题。定期练习会帮助你轻松应对测试和考试。

8- Ask Questions

8- 提问

Having questions while studying a subject or topic is not something out of the ordinary. If you have doubts about concepts, you must ask your teachers or peers about them. This will help you get rid of the uncertainty and prepare well for exams without doubts.
学习一门学科或一个主题时产生疑问是很正常的。如果你对概念有疑问，必须向老师或同学请教。这将帮助你消除疑惑，毫无顾虑地为考试做好准备。

You can also use an online calculus tutoring service if you’re uncomfortable with asking questions in class.
如果你不喜欢在课堂上提问，你也可以使用在线微积分辅导服务。

Besides that, you may also use a reference book for checking concepts. Using various methods is best to get rid of doubts and master calculus.
此外，你也可以使用参考书来核对概念。最好用多种方法来消除疑惑，掌握微积分。

9- Teach Others

9- 教别人

Another best way to learn calculus is by teaching others. You may form a study group with friends and help them with their concepts. The best thing is that if you teach something incorrectly, others may point it out.
学习微积分的另一个好方法是教别人。你可以和朋友组成学习小组，帮助他们理解概念。最好的是，如果你教错了什么，别人可能会指出来。

Teaching other students is also an effective way to test your understanding. It will allow you to know the concepts you understand completely. You will also know the topics that require improvement.
教其他学生也是检验你理解程度的有效方法。它会让你知道哪些概念你完全理解了，也会让你知道哪些主题需要改进。

Studying with a group will also enable you to solve more questions within a day. You may also try to help people on the social media group of your batch. Many students share problems on WhatsApp groups which is another effective way to learn.
和小组一起学习还能让你在一天内解决更多问题。你也可以尝试在你的班级社交媒体群里帮助别人。许多学生在 WhatsApp 群里分享问题，这也是另一种有效的学习方式。

10- Start Preparing Early For Exams

10- 提前开始为考试做准备

Many people delay exam preparation until the last minute because of the pressure of other subjects. However, that will not work when doing calculus.
很多人因为其他学科的压力，把考试准备推迟到最后一刻。但是，学习微积分时，这样做是行不通的。

You must start preparing at least one week before the exam week starts. This is advisable for students who have memorized and cleared their concepts beforehand. So the only thing left to do would be practice.
你必须至少在考试周开始前一周就开始准备。这对于那些事先已经记住并理清概念的学生是明智的。这样剩下要做的就只有练习了。

If your concepts are unclear, you must start studying at least a month before the exam.
如果你的概念不清楚，你必须至少在考试前一个月就开始学习。

Final Words

最后的话

These are the ten best ways to learn calculus. You must review the basic concepts of math before starting this subject.
以上是学习微积分的十个最佳方法。在开始学习这门学科之前，你必须复习数学的基本概念。

Viewing the syllabus outline and knowing the concepts you must learn during calculus is also advisable.
查看教学大纲，了解在微积分学习中必须掌握的概念也是明智的。

How to learn calculus (6 easy steps)

如何学习微积分（6 个简单步骤）

Calculus is the base for advanced math courses, and we use it widely in engineering, scientific research, and technology. Learning and mastering calculus is pertinent to your education and career success.
微积分是高等数学课程的基础，在工程、科学研究和技术领域中有着广泛的应用。学习并掌握微积分与你的教育和职业成功息息相关。

Most students struggle with calculus because it is very conceptual and application-based. You need to “feel” the calculus concepts via graphs, diagrams and correlate with real-life situations to master them.
大多数学生在微积分学习中遇到困难，是因为它非常注重概念和应用。你需要通过图形、图表来 “感受” 微积分概念，并将其与现实生活场景联系起来，才能掌握它们。

In this post, we will discuss how to learn calculus online on your own from scratch, fast and easy. We will discuss several tricks and tips that will help you do so.
在本文中，我们将探讨如何从零开始快速轻松地在线自学微积分。我们会介绍一些有助于学习的技巧和方法。

Step 1. Master PreCalculus, especially graph plotting

步骤 1：精通预微积分，尤其是图形绘制

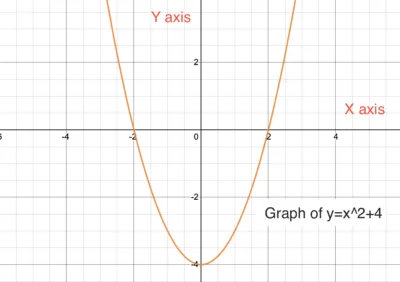
在这里插入图片描述

There is a saying, “well begun is half done.” If you want to master calculus, then your base must be strong. You need to master the PreCalculus course to strengthen your base, especially the graph plotting concepts. (Precalculus starts from grade 11th. )
俗话说：“好的开始是成功的一半。” 如果你想精通微积分，那么你的基础必须扎实。你需要掌握预微积分课程来巩固基础，尤其是图形绘制的概念。（预微积分从 11 年级开始。）

If you don’t know how to plot graphs of various functions, be it algebraic, trigonometric, exponential, or otherwise, you will struggle with even calculus 1, which is the most basic course on calculus 1.
如果你不知道如何绘制各种函数的图形，无论是代数函数、三角函数、指数函数还是其他函数，你甚至会在微积分 1（最基础的微积分课程）的学习中遇到困难。

Graph plotting does not mean that you have to take the long way of using 10 to 20 points and plotting each point from scratch. There are several tricks to plot the graph without using a single point. For example, if you already know the graph of y=x², which is a concave up parabola, you can easily plot the graph of y+2=x² just by shifting the origin. Tricks like this will save enormous time and make you more comfortable in graph plotting. To learn graph plotting tricks in calculus in detail, you can check this video .
图形绘制并不意味着你必须采用繁琐的方法，用 10 到 20 个点，逐个从头绘制。有一些技巧可以让你不用一个点就能画出图形。例如，如果你已经知道 y=x² 的图形是一条向上凹的抛物线，那么你只需通过平移原点，就能轻松画出 y+2=x² 的图形。这样的技巧会节省大量时间，让你在图形绘制上更加得心应手。想要详细学习微积分中的图形绘制技巧，可以查看这个视频。

Step 2. Graphical interpretation of differentiation

步骤 2：微分的图形解释

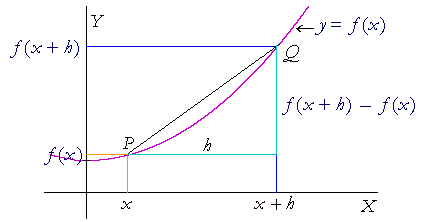
在这里插入图片描述

The diagram above gives a graphical interpretation of differentiation. Image credit the math page
上图给出了微分的图形解释。图片来源：the math page

We understand that there are other topics like limits, continuity, etc. before differentiation is introduced in calculus. Still, the most important is a graphical interpretation of differentiation (as a measure of rate change). Unless you master this concept, you will not learn the applications of derivatives (especially in complicated situations).
我们知道，在微积分中引入微分之前，还有极限、连续性等其他主题。不过，最重要的是微分的图形解释（作为变化率的度量）。除非你掌握了这个概念，否则你无法学会导数的应用（尤其是在复杂情况下）。

The first derivative (d/dx) is the slope or tangent at a given point on a graph. We also call it tan (θ), where θ is the tangent’s angle with the positive x-axis. This concept is instrumental in solving many geometry-related problems, especially physics and engineering.
一阶导数（d/dx）是图形上某一给定点的斜率或切线。我们也称之为 tan (θ)，其中 θ 是切线与正 x 轴的夹角。这个概念在解决许多与几何相关的问题时非常有用，尤其是在物理和工程领域。

Step 3. Learn applications of integrals

步骤 3：学习积分的应用

Let us be frank; solving integration problems mathematically has no use in real life. Hence, learning integration techniques though essential is not the ultimate goal of studying integral calculus. We must learn how to apply integration to solve real-life problems. Integration is a technique for the summation of anything. If you want to find the area under a graph bounded by certain lines or other functions, you can use integration techniques.
坦白说，从数学角度解决积分问题在现实生活中没有实际用途。因此，虽然学习积分技巧很重要，但这并不是学习积分学的最终目标。我们必须学会如何应用积分来解决现实生活中的问题。积分是一种对任何事物进行求和的技巧。如果你想找到由某些直线或其他函数界定的图形下的面积，可以使用积分技巧。

Have you ever wondered where the formula S=4πR² (surface area of a sphere) came from? You can apply integration techniques learned in calculus 1 to find this formula. You can use it to find the volume of a sphere, the volume of a cone, and the area of an ellipse as well, to name a few.
你有没有想过 S=4πR²（球体的表面积）这个公式是怎么来的？你可以应用在微积分 1 中学到的积分技巧来推导这个公式。举几个例子，你还可以用积分来求球体的体积、圆锥的体积以及椭圆的面积等。

Step 4. Master Infinite series, convergence and divergence

步骤 4：掌握无穷级数、收敛与发散

To learn calculus 2, students struggle the most in Infinite series, convergence, and divergence concepts. For some students, it’s even more complicated than multivariable calculus or calculus 3.
在学习微积分 2 时，学生们在无穷级数、收敛和发散概念上遇到的困难最大。对一些学生来说，这甚至比多变量微积分（或微积分 3）还要复杂。

The only way you can master these concepts is by solving many problems. While solving problems, never get satisfied because you answered them correctly. It would be best to think about why one strategy was better than the other. Was it possible to use any different method to solve the same problem? If yes, would that have been better or worse? Try all possibilities to use the best strategy for similar problems in the future. Also, try to imagine them graphically and see if they make any sense or not. (So basically, you should analyze not only your failures but also your success.)
掌握这些概念的唯一方法是做大量的题。在解题时，不要因为答对了就满足。你最好思考为什么一种策略比另一种更好。有没有可能用不同的方法来解决同一个问题？如果有，那种方法会更好还是更差？尝试所有可能性，以便在未来解决类似问题时能采用最佳策略。另外，试着从图形上想象它们，看看是否有意义。（所以基本上，你不仅要分析失败，还要分析成功。）

Step 5. Learn the graphical meaning of differential equations

步骤 5：学习微分方程的图形意义

Did you know that you can solve differential equations graphically too? Many students give more importance to learning higher differential equations mathematically, and they forget the graphical approach completely. Although we can not use the graphical method for all the problems in any meaningful way, mastering its concept is vital to understanding higher-level differential equations. Everything we study is there for a reason, and it is there to solve real-life problems, and if we don’t know about it, our complete understanding of the subject remains shallow at best.
你知道吗？微分方程也可以用图形来求解。许多学生更重视从数学角度学习高阶微分方程，却完全忽略了图形方法。尽管我们不能用图形方法有意义地解决所有问题，但掌握其概念对于理解高阶微分方程至关重要。我们所学的一切都有其存在的原因，都是为了解决现实生活中的问题，如果我们不了解这一点，我们对这门学科的理解充其量也只是肤浅的。

在这里插入图片描述

Step 6. Learn graph plotting for 3D functions

步骤 6：学习三维函数的图形绘制

The only reason why people find calculus 3 or multivariable calculus hard is because they do not know how to plot graphs in 3D. If we have x,y,z as variables, we can no longer plot the actual graphs on paper. Of course, we can use x,y,z axes to draw it on paper, but it will only be representative and not actual. Many students fail to master 3D graph plotting on paper, and hence they always struggle with calculus 3/multivariable calculus .
人们觉得微积分 3 或多变量微积分难，唯一的原因是他们不知道如何绘制三维图形。如果我们有 x、y、z 作为变量，就无法在纸上绘制出实际的图形了。当然，我们可以用 x、y、z 轴在纸上画出来，但这只是示意性的，并非实际图形。许多学生没能掌握在纸上绘制三维图形的方法，因此他们在学习微积分 3 / 多变量微积分时总是很吃力。

We suggest using a 3D plotter to help you understand the 3D graphs. Do so till you learn how to draw it on your own on paper. There is no shortcut, and you have to practice it. The more you practice, the more perfect you will become.
我们建议使用三维绘图仪来帮助你理解三维图形。一直用到你学会自己在纸上绘制为止。没有捷径可走，你必须多加练习。练习得越多，你就会越熟练。

Some FAQs

一些常见问题

How long does it take to learn calculus?

学习微积分需要多长时间？

Depending on how much time you devote and what you already know, you may need anywhere from 6 months to 3 years to master higher-level calculus. Precalculus may take 2 weeks to 4 months, and Calculus 1, Calculus 2, calculus 3, and differential equations will take the same 3 months to 1 year each.
根据你投入的时间和已有的知识水平，你可能需要 6 个月到 3 年的时间来掌握高阶微积分。预微积分可能需要 2 周到 4 个月，而微积分 1、微积分 2、微积分 3 和微分方程每门可能各需要 3 个月到 1 年的时间。

Which is the best book on Calculus?

最好的微积分教材是哪本？

Calculus Early Transcendentals 8th Edition by James Stewart Publisher - Cengage Learning Stewart calculus, early transcendentals, is undoubtedly the most popular and most recommended book on calculus.
詹姆斯・斯图尔特（James Stewart）所著的《微积分：早期超越函数》第 8 版，出版商为圣智学习（Cengage Learning）。毫无疑问，斯图尔特的《微积分：早期超越函数》是最受欢迎且推荐度最高的微积分教材。

Summary

总结

So this was all about learning calculus. We covered basic and advanced calculus courses like calculus 1, calculus 2, calculus 3, and differential equations. We mentioned the six most common hurdles that you as a student would face to learn higher-level calculus on your own ( from scratch) and how to cross those hurdles.
以上就是关于学习微积分的全部内容。我们涵盖了基础和高级微积分课程，如微积分 1、微积分 2、微积分 3 和微分方程。我们提到了作为学生，在从零开始自学高阶微积分时会遇到的六个最常见的障碍，以及如何克服这些障碍。

My Engineering Buddy team wishes you all the best in your calculus learning. Whether you are on your own or have a tutor, these tips will help you master calculus. It is helpful for both AP Calculus AB , AP calculus BC aspirants and those already studying in colleges and for beginners and advanced students alike.
“我的工程伙伴” 团队祝愿你在微积分学习中一切顺利。无论你是自学还是有导师指导，这些技巧都将帮助你精通微积分。这对 AP 微积分 AB、AP 微积分 BC 的备考者，以及已经上大学的学生，无论是初学者还是高阶学习者，都同样有帮助。

如何学好微积分

符克麦

什么是微积分?

微积分的起源可追溯至 17 世纪，当时牛顿和莱布尼兹独立地解决了以下两个重要的问题:

切线问题：给定一个函数 f 和函数图形 $y = f (x)$ 上的一点 P ，这个问题是要求一条和 $y = f (x)$ "局部分享恰於点"的直线的方程式。这条线称为 $y = f (x)$ 在 P 点的切线。
面积问题：给定一个定义在 $[a ， b]$ 上的非负函数 f ，这个问题是要计算在由函数图形 $y = f (x)$ ，轴， $x = a$ 以及 $x = b$ 所围出区域的面积。

这两个问题的解答可以利用下述的方式逼近：对於切线问题，在函数图形 $y = f (x)$ 上选择异於 P 点而非常接近 P 点的另一点 Q，然后计算通过 P 点和 Q 点的直线方程式(这很简单)，这条线就会非常接近我们想要的切线；对於面积问题，可以在考虑的区域内接有限个长方形，当长方形的个数够多时，这些长方形的面积和(这计算也不太困难)将会非常接近我们想要计算的面积。

现在，我们明確地知道要如何得到这两个问题的解答: 对於切线问题，让 Q 愈来愈接近 P；对於面积问题，让内接的长方形个数愈来愈多，直到能填满这个区域。

这就是牛顿和莱布尼兹的成就，他们对於上述的问题给出精确的数学意义，进而解决了问题。他们的答案在数学的发展上有著巨大的衝击。切线问题的解答导致了微分理论的发展；而面积问题导致了积分理论的发展。这两个理论，和它们的延伸及应用被统称为微积分。

更广泛地说，微积分的发展可以被视为近代数学的发展起源。

如何学好微积分?

学数学绝不容易！

欧几里德的名言-「几何学里没有王者之路」(There is no other Royal path which leads to geometry)，

意即学习几何学没有捷径，当然有关数学的所有领域，也必是如此。然而，倘若你能对学习数学，抱持著高度的兴趣和热情的心，相信很多困难将迎刃而解。以下提供一些关於如何学习微积分的具体建议。

试著自己解题。学数学唯一的好方法是由「做」中学。由於解题时，你必须把学过的理论再重新思考过一次，这个过程会让你学到如何从不同的角度来看这些理论，也会帮助你发现先前所忽略的东西。所以，尽可能多试著先由自己来解题。
解复杂习题时和其他同学一起努力。在十七、十八世纪时的数学家，他们的研究多半是单打独斗的成果；反观今日，有蛮大比例的研究是靠团队合作而产生的结果，团队合作的好处是让思考能够更加周全。当你遇到复杂的习题无法自己算出答案时，建议你可和其他同学一起討论，一群人的脑力激盪可能会促使你想出自己一个人孤军奋斗时所没有办法想到的点子。
和其他同学或老师一起討论课程内容。每个人都有自己习惯的看事情方式，往往一不小心就会落入盲点而不自知。所以，即便你认为你已经了解课程内容，建议你还是应该多和其他同学或是老师共同討论；这样一来，你才能察觉你忽略的小细节，或者一些你根本没有考虑到的层面。
课堂上要勇於发问。上课时，如果你有任何疑问，应该立即发问。因为你的问题，有可能正好就是其他同学不敢问的问题；也有可能是在坐所有的人(包括老师)都还没考虑到的问题。课堂上发问，不仅能对自己也是对全班同学的莫大帮助。一个活泼生动的学习环境，不单是只靠老师来营造，也需要同学们的参与，老师们都很希望也很重视同学们在课堂上能够有更主动的表现。相信这样互动的学习过程，一定能让你在学习微积分上有更多的收获。

为什么要学微积分?

或许你对微积分不是那么有兴趣，或许你来这里，是想学一些跟微积分无直接相关的知识，关於学习微积分，你的心中一定有很多疑惑。但是，问「为什么要学微积分?」，其实就好像问「为什么要学数学?」是一样的意思。怎么说呢? 因为微积分是现代数学的发展起点，主修科学相关领域的学

数学是科学的语言！想想看，如果你到了一个陌生的国家却不会说当地的语言。当然，你可以完全不学或只学你需要用到的几个字就能舒服地在那里生活好几年。可是，这样会限制你的生活，限制你对所处环境的了解，当窥这个环境的全貌，许多应该属於你的机会可能在你浑然不知的状况下悄悄溜走。科学的学习状况和这个例子很类似，或许你可以只学习一小部分的数学，就能满足获得某个领域知识的需求；但是没有好好学数学，你所获得部分还是有所限的，因为你將无法了解更广更深的部份。书到用时方恨少，数学亦然!

数学训练逻辑思考！这点十分重要。逻辑思考的能力不管它是不是与生俱来的，但很確定的一点是，它是可以被训练的，方法之一就是透过学习数学。数学解题会教你如何接近问题、学到如何抽丝剥茧地看出问题的关键、问出適切的问题、从不同的角度来思考问题等等。逻辑思考的能力比数学有用太多，例如它对学新的语言、组织与计画等也很有帮助。

总而言之，每位学生都应该而且可以为微积分找到学习动机。你不必认同「微积分是人类最伟大的成就之一，这个理论之美让人目眩神迷」。但至少把微积分看作是掌握学科的重要工具，而且是教你学习如何有系统地进攻与解决问题的重要理论。

本文译自符克麦老师网页的文章，原文请见
http://jupiter.math.nctu.edu.tw/~mfuchs/2005FallCalculus A()/index.html

微积分常用述语中英对照

A
absolute value	绝对值
argument	辐角
approach	趋近
antiderivatives	反导函数

B

C
conditional inequality	条件不等式
Chain Rule	连锁定律
contradictory linear equations	矛盾方程组
Complex numbers	复数
Conclusion(delete)	结论(delete)
converge	收敛
curve	曲线
calculus	微积分

D
domain	定义域
denominator	分数
derivative	导数
dependent linear equations	相依方程式
discriminant	判別式
difference set	差集
dividend	被除数
divisor	除数
divergent	发散
differentiation	微分

E
exponent	指数
exponential law	指数率
exponential function	指数函数
extreme values of functions	函数的极值
expression	函数表示法
empty set	空集合
equation	方程式

F
function	函数

G
graphical solution	图解法
Gaussian function	高斯函数

H
hypotenuse	斜边
hypothesis	假设

I
inverse function	反函数
interval	区间
infinity	无限大
irrational number	无理数
inference	推理
integration	积分
integral exponent	整数指数

J

K

L
linear inequality in two unknown variables	二元一次不等式
limit	极限
logarithmic Functions	对数函数

M
maximum	极大值
minimum	极小值
matrix	矩阵
multiple	倍数

N
Newton’s Method	牛顿法
normal vector	法线向量
numerator	分子

O
origin	原点

P
polar coordinate	极座標
property	极点
property	性质
polynomial function	多项函数
parameter	参数
perpendicular	垂直
parabola	拋物线

Q
quotient	商

R
range	值域
rational function	有理函数
real number	实数
remainder	余数
root	根
radian	弧度

S
solution	解
solution set	解集合
slope	斜率
series	级数
symmetry	对称
sequence	数列

T
tangent line	切线
trigonometric function	三角函数

U

V
value	函数值
vector	向量
vertex	顶点

W

X

Y

Z