注:本文为“三角函数”相关合辑。
略作重排,未整理去重。
如有内容异常,请看原文。
三角函数及其常用公式
天天睡大觉 已于 2025-06-20 22:55:56 修改
基本信息
三角函数 是数学中初等函数的一类,属于超越函数。它们将任意角映射为对应比值,通常在平面直角坐标系中定义,定义域为整个实数域。
虽然三角函数种类繁多,但只要掌握其本质与内在规律,就能发现它们之间强大的联系。理解这些规律是学习三角函数的关键。
常用三角函数定义

| 函数名 | 表达式 | 发音/说明 |
|---|---|---|
| 正弦 sine | sin α = b c \sin\alpha = \dfrac{b}{c} sinα=cb | [sain] |
| 余弦 cosine | cos α = a c \cos\alpha = \dfrac{a}{c} cosα=ca | [kəusain] |
| 正切 tangent | tan α = b a \tan\alpha = \dfrac{b}{a} tanα=ab | ['tændʒənt] |
| 余切 cotangent | cot α = a b \cot\alpha = \dfrac{a}{b} cotα=ba | ['kəu’tændʒənt] |
| 正割 secant | sec α = c a \sec\alpha = \dfrac{c}{a} secα=ac | ['si:kənt] |
| 余割 cosecant | csc α = c b \csc\alpha = \dfrac{c}{b} cscα=bc | ['kau’si:kənt] |
三角函数基本关系
- tan α ⋅ cot α = 1 \tan\alpha \cdot \cot\alpha = 1 tanα⋅cotα=1
- sin α ⋅ csc α = 1 \sin\alpha \cdot \csc\alpha = 1 sinα⋅cscα=1
- cos α ⋅ sec α = 1 \cos\alpha \cdot \sec\alpha = 1 cosα⋅secα=1
- sin α cos α = tan α \dfrac{\sin\alpha}{\cos\alpha} = \tan\alpha cosαsinα=tanα
- sin 2 α + cos 2 α = 1 \sin^2\alpha + \cos^2\alpha = 1 sin2α+cos2α=1
特殊角三角函数值
| 角度 | sin \sin sin | cos \cos cos | tan \tan tan |
|---|---|---|---|
| 1 5 ∘ 15^\circ 15∘ | 6 − 2 4 \dfrac{\sqrt{6}-\sqrt{2}}{4} 46−2 | 6 + 2 4 \dfrac{\sqrt{6}+\sqrt{2}}{4} 46+2 | 2 − 3 2-\sqrt{3} 2−3 |
| 3 0 ∘ 30^\circ 30∘ | 1 2 \dfrac{1}{2} 21 | 3 2 \dfrac{\sqrt{3}}{2} 23 | 3 3 \dfrac{\sqrt{3}}{3} 33 |
| 4 5 ∘ 45^\circ 45∘ | 2 2 \dfrac{\sqrt{2}}{2} 22 | 2 2 \dfrac{\sqrt{2}}{2} 22 | 1 1 1 |
| 6 0 ∘ 60^\circ 60∘ | 3 2 \dfrac{\sqrt{3}}{2} 23 | 1 2 \dfrac{1}{2} 21 | 3 \sqrt{3} 3 |
| 18 0 ∘ 180^\circ 180∘ | 0 0 0 | − 1 -1 −1 | 0 0 0 |
重要定理
正弦定理
在三角形
△
A
B
C
\triangle ABC
△ABC 中,有
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R
sinAa=sinBb=sinCc=2R
其中,
R
R
R 为
△
A
B
C
\triangle ABC
△ABC 的外接圆半径。
推导:

如上图所示,在
△
A
B
C
\triangle ABC
△ABC 中,作辅助线
C
D
CD
CD 垂直于
A
B
AB
AB,则有
C
D
=
b
sin
A
=
a
sin
B
CD = b \sin A = a \sin B
CD=bsinA=asinB
因此,
a
sin
A
=
b
sin
B
\frac{a}{\sin A} = \frac{b}{\sin B}
sinAa=sinBb
同理可证:
a
sin
A
=
c
sin
C
\frac{a}{\sin A} = \frac{c}{\sin C}
sinAa=sinCc
故
a
sin
A
=
b
sin
B
=
c
sin
C
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
sinAa=sinBb=sinCc
进一步,作
△
A
B
C
\triangle ABC
△ABC 的外接圆,圆心为
O
O
O,连接
C
O
CO
CO 并延长,交外接圆于点
E
E
E,连接
A
E
AE
AE。根据直径所对圆周角为直角以及同弧所对圆周角相等的性质,可得:
∠
C
A
E
=
9
0
∘
,
∠
E
=
∠
B
\angle CAE = 90^\circ, \quad \angle E = \angle B
∠CAE=90∘,∠E=∠B
因此,
sin
B
=
sin
E
=
b
2
R
\sin B = \sin E = \frac{b}{2R}
sinB=sinE=2Rb
从而,
b
sin
B
=
2
R
\frac{b}{\sin B} = 2R
sinBb=2R
综上所述,
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R
sinAa=sinBb=sinCc=2R
余弦定理
在三角形
△
A
B
C
\triangle ABC
△ABC 中,有
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
c^2 = a^2 + b^2 - 2ab \cos C
c2=a2+b2−2abcosC
其中,
C
C
C 为边
a
a
a 与边
b
b
b 的夹角。
推导:

如上图所示,在
△
A
B
C
\triangle ABC
△ABC 中,作辅助线
C
D
CD
CD 垂直于
A
B
AB
AB,则有
c
=
b
cos
A
+
a
cos
B
c = b \cos A + a \cos B
c=bcosA+acosB
两边同时乘以
c
c
c,得
c
2
=
b
c
cos
A
+
a
c
cos
B
c^2 = bc \cos A + ac \cos B
c2=bccosA+accosB
同理可得:
b
=
c
cos
A
+
a
cos
C
,
a
=
b
cos
C
+
c
cos
B
b = c \cos A + a \cos C, \quad a = b \cos C + c \cos B
b=ccosA+acosC,a=bcosC+ccosB
进一步,
b
2
=
b
c
cos
A
+
a
b
cos
C
,
a
2
=
a
b
cos
C
+
a
c
cos
B
b^2 = bc \cos A + ab \cos C, \quad a^2 = ab \cos C + ac \cos B
b2=bccosA+abcosC,a2=abcosC+accosB
将上述两式相加,得
a
2
+
b
2
=
c
2
+
2
a
b
cos
C
a^2 + b^2 = c^2 + 2ab \cos C
a2+b2=c2+2abcosC
因此,
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
c^2 = a^2 + b^2 - 2ab \cos C
c2=a2+b2−2abcosC
常用公式
三角函数的诱导公式(六组公式)
| 编号 | 内容 |
|---|---|
| 公式一 |
sin
(
α
+
2
k
π
)
=
sin
α
\sin(\alpha + 2k\pi) = \sin\alpha
sin(α+2kπ)=sinα cos ( α + 2 k π ) = cos α \cos(\alpha + 2k\pi) = \cos\alpha cos(α+2kπ)=cosα tan ( α + 2 k π ) = tan α \tan(\alpha + 2k\pi) = \tan\alpha tan(α+2kπ)=tanα |
| 公式二 |
sin
[
(
2
k
+
1
)
π
+
α
]
=
−
sin
α
\sin[(2k+1)\pi + \alpha] = -\sin\alpha
sin[(2k+1)π+α]=−sinα cos [ ( 2 k + 1 ) π + α ] = − cos α \cos[(2k+1)\pi + \alpha] = -\cos\alpha cos[(2k+1)π+α]=−cosα tan [ ( 2 k + 1 ) π + α ] = tan α \tan[(2k+1)\pi + \alpha] = \tan\alpha tan[(2k+1)π+α]=tanα |
| 公式三 |
sin
(
2
k
π
−
α
)
=
−
sin
α
\sin(2k\pi - \alpha) = -\sin\alpha
sin(2kπ−α)=−sinα cos ( 2 k π − α ) = cos α \cos(2k\pi - \alpha) = \cos\alpha cos(2kπ−α)=cosα tan ( 2 k π − α ) = − tan α \tan(2k\pi - \alpha) = -\tan\alpha tan(2kπ−α)=−tanα |
| 公式四 |
sin
[
(
2
k
+
1
)
π
−
α
]
=
sin
α
\sin[(2k+1)\pi - \alpha] = \sin\alpha
sin[(2k+1)π−α]=sinα cos [ ( 2 k + 1 ) π − α ] = − cos α \cos[(2k+1)\pi - \alpha] = -\cos\alpha cos[(2k+1)π−α]=−cosα tan [ ( 2 k + 1 ) π − α ] = − tan α \tan[(2k+1)\pi - \alpha] = -\tan\alpha tan[(2k+1)π−α]=−tanα |
| 公式五 |
sin
(
2
π
−
α
)
=
−
sin
α
\sin(2\pi - \alpha) = -\sin\alpha
sin(2π−α)=−sinα cos ( 2 π − α ) = cos α \cos(2\pi - \alpha) = \cos\alpha cos(2π−α)=cosα tan ( 2 π − α ) = − tan α \tan(2\pi - \alpha) = -\tan\alpha tan(2π−α)=−tanα |
| 公式六 |
sin
(
π
2
±
α
)
=
cos
α
\sin\left(\frac{\pi}{2} \pm \alpha\right) = \cos\alpha
sin(2π±α)=cosα cos ( π 2 ± α ) = ∓ sin α \cos\left(\frac{\pi}{2} \pm \alpha\right) = \mp \sin\alpha cos(2π±α)=∓sinα tan ( π 2 ± α ) = ∓ cot α \tan\left(\frac{\pi}{2} \pm \alpha\right) = \mp \cot\alpha tan(2π±α)=∓cotα |
诱导公式记背诀窍:奇变偶不变,符号看象限。
或者也可以这样记:分变整不变,符号看象限。
积化和差的四个公式
sin α cos β = sin ( α + β ) + sin ( α − β ) 2 , cos α sin β = sin ( α + β ) − sin ( α − β ) 2 , cos α cos β = cos ( α + β ) + cos ( α − β ) 2 , sin α sin β = − cos ( α + β ) − cos ( α − β ) 2 . \begin{aligned} \sin \alpha \cos \beta &= \frac{\sin(\alpha + \beta) + \sin(\alpha - \beta)}{2}, \\ \cos \alpha \sin \beta &= \frac{\sin(\alpha + \beta) - \sin(\alpha - \beta)}{2}, \\ \cos \alpha \cos \beta &= \frac{\cos(\alpha + \beta) + \cos(\alpha - \beta)}{2}, \\ \sin \alpha \sin \beta &= -\frac{\cos(\alpha + \beta) - \cos(\alpha - \beta)}{2}. \end{aligned} sinαcosβcosαsinβcosαcosβsinαsinβ=2sin(α+β)+sin(α−β),=2sin(α+β)−sin(α−β),=2cos(α+β)+cos(α−β),=−2cos(α+β)−cos(α−β).
推导:

图一:展示了矩形
A
B
D
F
ABDF
ABDF 和相关角度的几何关系,用于推导正弦和余弦的和差公式。
在图中,设 A B D F ABDF ABDF 为矩形, ∠ A C E = 9 0 ∘ \angle ACE = 90^\circ ∠ACE=90∘, ∠ C A E = α \angle CAE = \alpha ∠CAE=α, ∠ B A C = β \angle BAC = \beta ∠BAC=β。则有 ∠ A E F = α + β \angle AEF = \alpha + \beta ∠AEF=α+β, ∠ D C E = β \angle DCE = \beta ∠DCE=β。设 A E = 1 AE = 1 AE=1,则有:
A F = sin ( α + β ) , C E = sin α , A C = cos α , C D = sin α cos β , B C = cos α sin β , E F = cos ( α + β ) , D E = sin α sin β , A B = cos α cos β . \begin{aligned} AF &= \sin(\alpha + \beta), \\ CE &= \sin \alpha, \\ AC &= \cos \alpha, \\ CD &= \sin \alpha \cos \beta, \\ BC &= \cos \alpha \sin \beta, \\ EF &= \cos(\alpha + \beta), \\ DE &= \sin \alpha \sin \beta, \\ AB &= \cos \alpha \cos \beta. \end{aligned} AFCEACCDBCEFDEAB=sin(α+β),=sinα,=cosα,=sinαcosβ,=cosαsinβ,=cos(α+β),=sinαsinβ,=cosαcosβ.
由 A F = B D AF = BD AF=BD 可得:
sin ( α + β ) = sin α cos β + cos α sin β . \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta. sin(α+β)=sinαcosβ+cosαsinβ.
由 A B = D F AB = DF AB=DF 可得:
cos ( α + β ) = cos α cos β − sin α sin β . \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta. cos(α+β)=cosαcosβ−sinαsinβ.
因此,可以推导出:
sin ( α − β ) = sin α cos β − cos α sin β , cos ( α − β ) = cos α cos β + sin α sin β . \begin{aligned} \sin(\alpha - \beta) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta, \\ \cos(\alpha - \beta) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta. \end{aligned} sin(α−β)cos(α−β)=sinαcosβ−cosαsinβ,=cosαcosβ+sinαsinβ.
进一步,可以得到积化和差公式:
sin α cos β = sin ( α + β ) + sin ( α − β ) 2 , cos α sin β = sin ( α + β ) − sin ( α − β ) 2 , cos α cos β = cos ( α + β ) + cos ( α − β ) 2 , sin α sin β = − cos ( α + β ) − cos ( α − β ) 2 . \begin{aligned} \sin \alpha \cos \beta &= \frac{\sin(\alpha + \beta) + \sin(\alpha - \beta)}{2}, \\ \cos \alpha \sin \beta &= \frac{\sin(\alpha + \beta) - \sin(\alpha - \beta)}{2}, \\ \cos \alpha \cos \beta &= \frac{\cos(\alpha + \beta) + \cos(\alpha - \beta)}{2}, \\ \sin \alpha \sin \beta &= -\frac{\cos(\alpha + \beta) - \cos(\alpha - \beta)}{2}. \end{aligned} sinαcosβcosαsinβcosαcosβsinαsinβ=2sin(α+β)+sin(α−β),=2sin(α+β)−sin(α−β),=2cos(α+β)+cos(α−β),=−2cos(α+β)−cos(α−β).

图二:展示了用于推导和差化积公式的几何图形。
和差化积的四个公式
sin a + sin b = 2 sin ( a + b 2 ) cos ( a − b 2 ) , sin a − sin b = 2 cos ( a + b 2 ) sin ( a − b 2 ) , cos a + cos b = 2 cos ( a + b 2 ) cos ( a − b 2 ) , cos a − cos b = − 2 sin ( a + b 2 ) sin ( a − b 2 ) . \begin{aligned} \sin a + \sin b &= 2 \sin\left(\frac{a + b}{2}\right) \cos\left(\frac{a - b}{2}\right), \\ \sin a - \sin b &= 2 \cos\left(\frac{a + b}{2}\right) \sin\left(\frac{a - b}{2}\right), \\ \cos a + \cos b &= 2 \cos\left(\frac{a + b}{2}\right) \cos\left(\frac{a - b}{2}\right), \\ \cos a - \cos b &= -2 \sin\left(\frac{a + b}{2}\right) \sin\left(\frac{a - b}{2}\right). \end{aligned} sina+sinbsina−sinbcosa+cosbcosa−cosb=2sin(2a+b)cos(2a−b),=2cos(2a+b)sin(2a−b),=2cos(2a+b)cos(2a−b),=−2sin(2a+b)sin(2a−b).
推导:
和差化积公式可以通过积化和差公式推导。设 α + β = a \alpha + \beta = a α+β=a, α − β = b \alpha - \beta = b α−β=b,则 α = a + b 2 \alpha = \frac{a + b}{2} α=2a+b, β = a − b 2 \beta = \frac{a - b}{2} β=2a−b。因此:
sin a = sin ( α + β ) = sin ( a + b 2 ) cos ( a − b 2 ) + cos ( a + b 2 ) sin ( a − b 2 ) , sin b = sin ( α − β ) = sin ( a + b 2 ) cos ( a − b 2 ) − cos ( a + b 2 ) sin ( a − b 2 ) , cos a = cos ( α + β ) = cos ( a + b 2 ) cos ( a − b 2 ) − sin ( a + b 2 ) sin ( a − b 2 ) , cos b = cos ( α − β ) = cos ( a + b 2 ) cos ( a − b 2 ) + sin ( a + b 2 ) sin ( a − b 2 ) . \begin{aligned} \sin a &= \sin(\alpha + \beta) = \sin\left(\frac{a + b}{2}\right) \cos\left(\frac{a - b}{2}\right) + \cos\left(\frac{a + b}{2}\right) \sin\left(\frac{a - b}{2}\right), \\ \sin b &= \sin(\alpha - \beta) = \sin\left(\frac{a + b}{2}\right) \cos\left(\frac{a - b}{2}\right) - \cos\left(\frac{a + b}{2}\right) \sin\left(\frac{a - b}{2}\right), \\ \cos a &= \cos(\alpha + \beta) = \cos\left(\frac{a + b}{2}\right) \cos\left(\frac{a - b}{2}\right) - \sin\left(\frac{a + b}{2}\right) \sin\left(\frac{a - b}{2}\right), \\ \cos b &= \cos(\alpha - \beta) = \cos\left(\frac{a + b}{2}\right) \cos\left(\frac{a - b}{2}\right) + \sin\left(\frac{a + b}{2}\right) \sin\left(\frac{a - b}{2}\right). \end{aligned} sinasinbcosacosb=sin(α+β)=sin(2a+b)cos(2a−b)+cos(2a+b)sin(2a−b),=sin(α−β)=sin(2a+b)cos(2a−b)−cos(2a+b)sin(2a−b),=cos(α+β)=cos(2a+b)cos(2a−b)−sin(2a+b)sin(2a−b),=cos(α−β)=cos(2a+b)cos(2a−b)+sin(2a+b)sin(2a−b).
因此,可以得到和差化积公式:
sin a + sin b = 2 sin ( a + b 2 ) cos ( a − b 2 ) , sin a − sin b = 2 cos ( a + b 2 ) sin ( a − b 2 ) , cos a + cos b = 2 cos ( a + b 2 ) cos ( a − b 2 ) , cos a − cos b = − 2 sin ( a + b 2 ) sin ( a − b 2 ) . \begin{aligned} \sin a + \sin b &= 2 \sin\left(\frac{a + b}{2}\right) \cos\left(\frac{a - b}{2}\right), \\ \sin a - \sin b &= 2 \cos\left(\frac{a + b}{2}\right) \sin\left(\frac{a - b}{2}\right), \\ \cos a + \cos b &= 2 \cos\left(\frac{a + b}{2}\right) \cos\left(\frac{a - b}{2}\right), \\ \cos a - \cos b &= -2 \sin\left(\frac{a + b}{2}\right) \sin\left(\frac{a - b}{2}\right). \end{aligned} sina+sinbsina−sinbcosa+cosbcosa−cosb=2sin(2a+b)cos(2a−b),=2cos(2a+b)sin(2a−b),=2cos(2a+b)cos(2a−b),=−2sin(2a+b)sin(2a−b).
三角和公式
sin ( α + β + γ ) = sin α cos β cos γ + cos α sin β cos γ + cos α cos β sin γ − sin α sin β sin γ cos ( α + β + γ ) = cos α cos β cos γ − cos α sin β sin γ − sin α cos β sin γ − sin α sin β cos γ tan ( α + β + γ ) = tan α + tan β + tan γ − tan α tan β tan γ 1 − tan α tan β − tan β tan γ − tan α tan γ \begin{aligned} \sin(\alpha + \beta + \gamma) &= \sin\alpha \cos\beta \cos\gamma + \cos\alpha \sin\beta \cos\gamma + \cos\alpha \cos\beta \sin\gamma - \sin\alpha \sin\beta \sin\gamma \\ \cos(\alpha + \beta + \gamma) &= \cos\alpha \cos\beta \cos\gamma - \cos\alpha \sin\beta \sin\gamma - \sin\alpha \cos\beta \sin\gamma - \sin\alpha \sin\beta \cos\gamma \\ \tan(\alpha + \beta + \gamma) &= \frac{\tan\alpha + \tan\beta + \tan\gamma - \tan\alpha \tan\beta \tan\gamma}{1 - \tan\alpha \tan\beta - \tan\beta \tan\gamma - \tan\alpha \tan\gamma} \end{aligned} sin(α+β+γ)cos(α+β+γ)tan(α+β+γ)=sinαcosβcosγ+cosαsinβcosγ+cosαcosβsinγ−sinαsinβsinγ=cosαcosβcosγ−cosαsinβsinγ−sinαcosβsinγ−sinαsinβcosγ=1−tanαtanβ−tanβtanγ−tanαtanγtanα+tanβ+tanγ−tanαtanβtanγ
特殊公式
( sin a + sin θ ) ( sin a − sin θ ) = sin ( a + θ ) sin ( a − θ ) (\sin a + \sin\theta)(\sin a - \sin\theta) = \sin(a + \theta)\sin(a - \theta) (sina+sinθ)(sina−sinθ)=sin(a+θ)sin(a−θ)
坡度公式
设坡面与水平面夹角为 α \alpha α,则坡度:
i = h l = tan α i = \frac{h}{l} = \tan\alpha i=lh=tanα
辅助角公式(收缩公式)
a sin α + b cos α = a 2 + b 2 ⋅ sin ( α + ϕ ) a \sin\alpha + b \cos\alpha = \sqrt{a^2 + b^2} \cdot \sin(\alpha + \phi) asinα+bcosα=a2+b2⋅sin(α+ϕ)
其中 tan ϕ = b a \tan\phi = \dfrac{b}{a} tanϕ=ab。
双曲函数
sinh a = e a − e − a 2 cosh a = e a + e − a 2 tanh a = sinh a cosh a \begin{aligned} \sinh a &= \frac{e^a - e^{-a}}{2} \\ \cosh a &= \frac{e^a + e^{-a}}{2} \\ \tanh a &= \frac{\sinh a}{\cosh a} \end{aligned} sinhacoshatanha=2ea−e−a=2ea+e−a=coshasinha
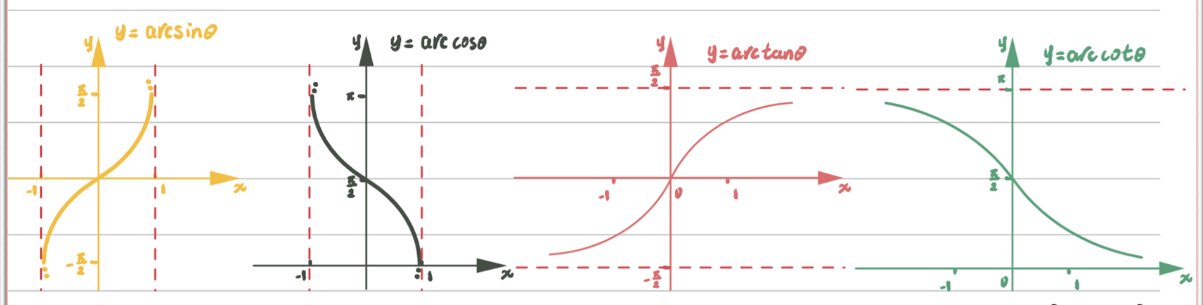
反三角函数公式
a r c s i n ( − x ) = − a r c s i n x a r c c o s ( − x ) = π − a r c c o s x a r c t a n ( − x ) = − a r c t a n x a r c c o t ( − x ) = π − a r c c o t x a r c s i n x + a r c c o s x = a r c t a n x + a r c c o t x = π 2 arcsin(-x) = -arcsin x \\[4pt] arccos(-x) = \pi - arccos x \\[4pt] arctan(-x) = -arctan x \\[4pt] arccot(-x) = \pi - arccot x \\[4pt] arcsin x + arccos x = arctan x + arccot x = \frac{\pi}{2} arcsin(−x)=−arcsinxarccos(−x)=π−arccosxarctan(−x)=−arctanxarccot(−x)=π−arccotxarcsinx+arccosx=arctanx+arccotx=2π
常用三角函数公式与反三角函数公式的证明
你要飞 已于 2025-06-01 16:08:18 修改
三角函数
定义
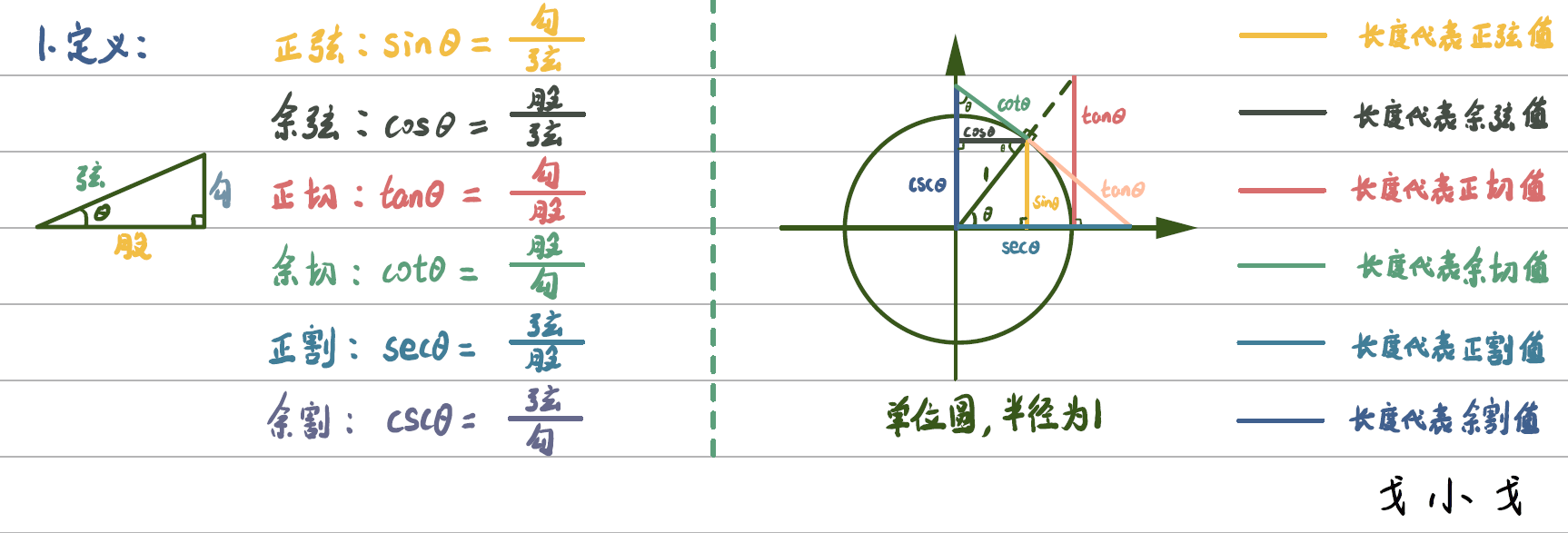
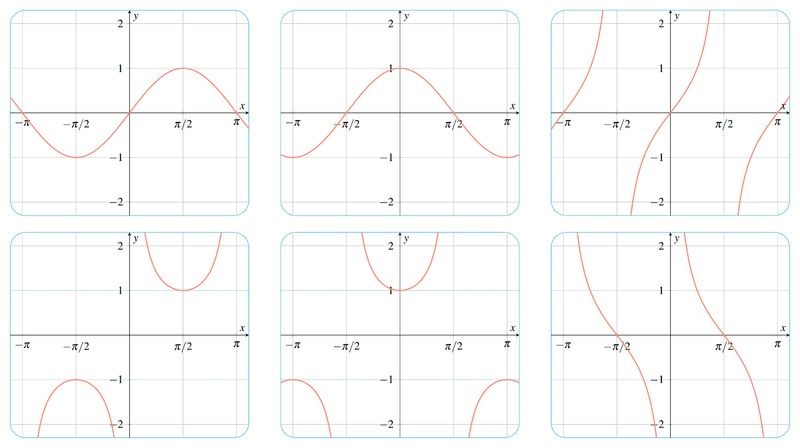
图像
六边形记忆法
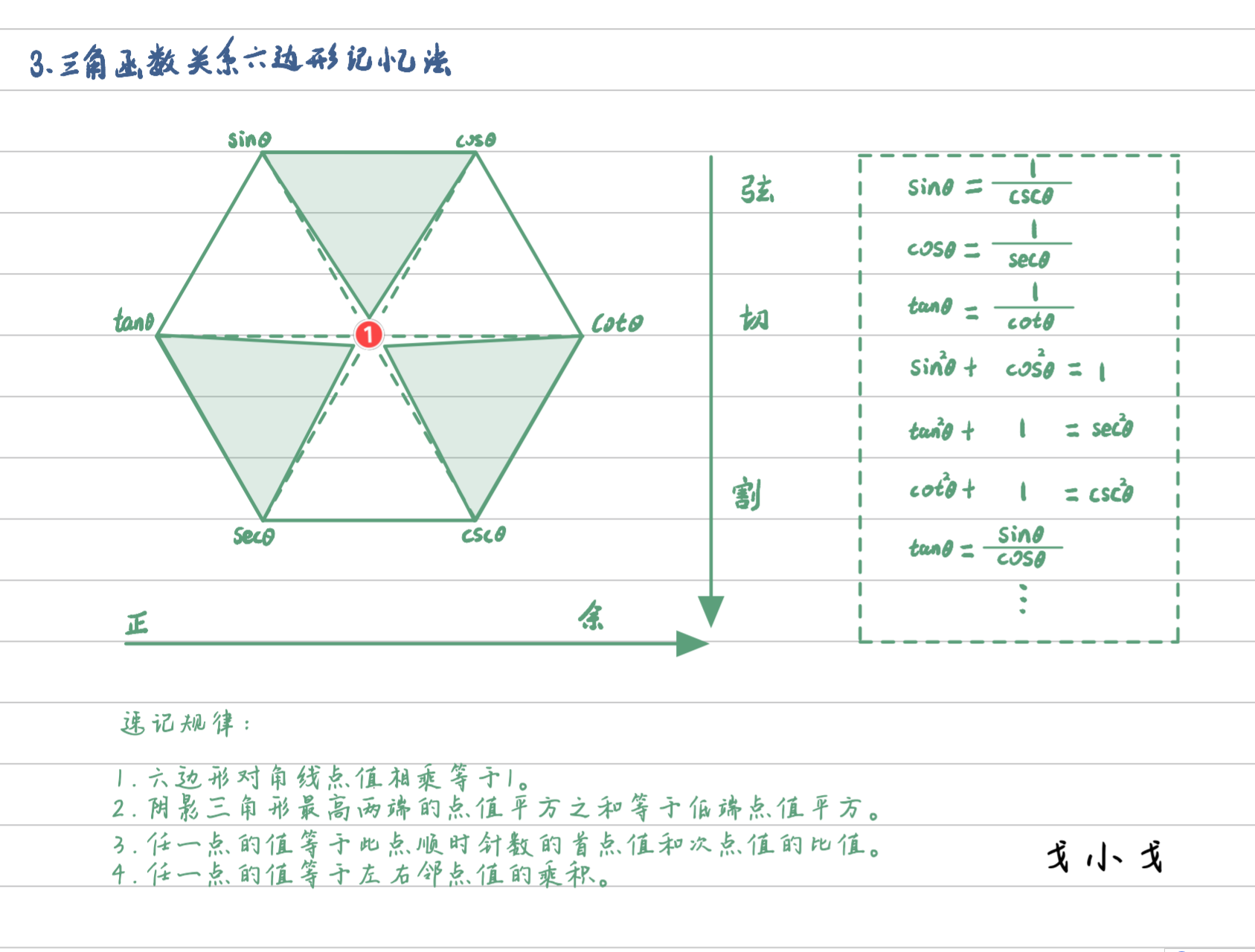
速记规律:
- 六边形对角线点值相乘等于 1
- 阴影三角形最高两端的点值平方之和等于低端点值平方
- 任一点值等于此点顺时针数的首点值和次点值的比值
- 任一点值等于左右邻点值的乘积
三角函数常用公式的证明
只需证明和差公式,其他公式均可由此推导。
AAA
和差公式几何证明
如图所示,在矩形 B E D F BEDF BEDF 中存在一个斜边长度为 1 的直角三角形 △ A C B \triangle ACB △ACB。求证:
{ sin ( α + β ) = sin α cos β + cos α sin β sin ( γ − β ) = sin γ cos β − cos γ sin β \begin{cases} \sin{(\alpha + \beta)} = \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta} \\ \sin{(\gamma - \beta)} = \sin{\gamma} \cos{\beta} - \cos{\gamma} \sin{\beta} \end{cases} {sin(α+β)=sinαcosβ+cosαsinβsin(γ−β)=sinγcosβ−cosγsinβ

证明:易得
α + β = ∠ E B A = ∠ F A B \alpha + \beta = \angle EBA = \angle FAB α+β=∠EBA=∠FAB
将 B F BF BF 平移至 A A A 点,有
B F = sin ( α + β ) , A F = cos ( α + β ) BF = \sin{(\alpha + \beta)}, \quad AF = \cos{(\alpha + \beta)} BF=sin(α+β),AF=cos(α+β)
其中
B F = E C + C D = B C sin ∠ E B C + A C cos ∠ D C A BF = EC + CD = BC \sin{\angle EBC} + AC \cos{\angle DCA} BF=EC+CD=BCsin∠EBC+ACcos∠DCA
A F = D F − D A = E B − D A = B C cos ∠ E B C − A C sin ∠ D C A AF = DF - DA = EB - DA = BC \cos{\angle EBC} - AC \sin{\angle DCA} AF=DF−DA=EB−DA=BCcos∠EBC−ACsin∠DCA
又
∠ E B C + ∠ B C E = ∠ B C E + ∠ D C A = π 2 \angle EBC + \angle BCE = \angle BCE + \angle DCA = \frac{\pi}{2} ∠EBC+∠BCE=∠BCE+∠DCA=2π
B C = cos β , A C = sin β BC = \cos{\beta}, \quad AC = \sin{\beta} BC=cosβ,AC=sinβ
因此
sin ( α + β ) = sin α cos β + cos α sin β \sin{(\alpha + \beta)} = \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta} sin(α+β)=sinαcosβ+cosαsinβ
cos ( α + β ) = cos α cos β − sin α sin β \cos{(\alpha + \beta)} = \cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta} cos(α+β)=cosαcosβ−sinαsinβ
两式相除得
tan ( α + β ) = tan α + tan β 1 − tan α tan β \tan{(\alpha + \beta)} = \frac{\tan{\alpha} + \tan{\beta}}{1 - \tan{\alpha} \tan{\beta}} tan(α+β)=1−tanαtanβtanα+tanβ
对于 sin ( γ − β ) \sin{(\gamma - \beta)} sin(γ−β),方法类似,当然也可以通过 γ = π 2 − α \gamma = \frac{\pi}{2} - \alpha γ=2π−α 和诱导公式来证明:
sin ( γ − β ) = cos ( α + β ) = cos α cos β − sin α sin β = sin γ cos β − cos γ sin β \sin{(\gamma - \beta)} = \cos{(\alpha + \beta)} = \cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta} = \sin{\gamma} \cos{\beta} - \cos{\gamma} \sin{\beta} sin(γ−β)=cos(α+β)=cosαcosβ−sinαsinβ=sinγcosβ−cosγsinβ
cos ( γ − β ) = sin ( α + β ) = sin α cos β + cos α sin β = cos γ cos β + sin γ sin β \cos{(\gamma - \beta)} = \sin{(\alpha + \beta)} = \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta} = \cos{\gamma} \cos{\beta} + \sin{\gamma} \sin{\beta} cos(γ−β)=sin(α+β)=sinαcosβ+cosαsinβ=cosγcosβ+sinγsinβ
tan ( γ − β ) = tan γ − tan β 1 + tan γ tan β \tan{(\gamma - \beta)} = \frac{\tan{\gamma} - \tan{\beta}}{1 + \tan{\gamma} \tan{\beta}} tan(γ−β)=1+tanγtanβtanγ−tanβ
和差公式的欧拉证明
用欧拉公式证明三角函数和差公式的核心在于利用指数函数与三角函数的关系,将复数乘法转化为三角函数运算。以下是具体证明过程:
欧拉公式为:
e i θ = cos θ + i sin θ e^{i\theta} = \cos\theta + i\sin\theta eiθ=cosθ+isinθ
其共轭形式为:
e − i θ = cos θ − i sin θ e^{-i\theta} = \cos\theta - i\sin\theta e−iθ=cosθ−isinθ
1. cos ( a + b ) \cos(a + b) cos(a+b) 和 sin ( a + b ) \sin(a + b) sin(a+b)
考虑 e i ( a + b ) e^{i(a + b)} ei(a+b),根据指数运算性质:
e i ( a + b ) = e i a ⋅ e i b e^{i(a + b)} = e^{ia} \cdot e^{ib} ei(a+b)=eia⋅eib
将右边展开为复数乘积:
( cos a + i sin a ) ( cos b + i sin b ) = cos a cos b + i cos a sin b + i sin a cos b + i 2 sin a sin b (\cos a + i\sin a)(\cos b + i\sin b) = \cos a \cos b + i\cos a \sin b + i\sin a \cos b + i^2 \sin a \sin b (cosa+isina)(cosb+isinb)=cosacosb+icosasinb+isinacosb+i2sinasinb
由于 i 2 = − 1 i^2 = -1 i2=−1,化简后得到:
cos a cos b − sin a sin b + i ( sin a cos b + cos a sin b ) \cos a \cos b - \sin a \sin b + i(\sin a \cos b + \cos a \sin b) cosacosb−sinasinb+i(sinacosb+cosasinb)
左边根据欧拉公式为:
e i ( a + b ) = cos ( a + b ) + i sin ( a + b ) e^{i(a + b)} = \cos(a + b) + i\sin(a + b) ei(a+b)=cos(a+b)+isin(a+b)
比较实部和虚部,得:
{ cos ( a + b ) = cos a cos b − sin a sin b sin ( a + b ) = sin a cos b + cos a sin b \begin{cases} \cos(a + b) = \cos a \cos b - \sin a \sin b \\ \sin(a + b) = \sin a \cos b + \cos a \sin b \end{cases} {cos(a+b)=cosacosb−sinasinbsin(a+b)=sinacosb+cosasinb
2. cos ( a − b ) \cos(a - b) cos(a−b) 和 sin ( a − b ) \sin(a - b) sin(a−b)
类似地,考虑 e i ( a − b ) e^{i(a - b)} ei(a−b):
e i ( a − b ) = e i a ⋅ e − i b e^{i(a - b)} = e^{ia} \cdot e^{-ib} ei(a−b)=eia⋅e−ib
展开右边:
( cos a + i sin a ) ( cos b − i sin b ) = cos a cos b − i cos a sin b + i sin a cos b − i 2 sin a sin b (\cos a + i\sin a)(\cos b - i\sin b) = \cos a \cos b - i\cos a \sin b + i\sin a \cos b - i^2 \sin a \sin b (cosa+isina)(cosb−isinb)=cosacosb−icosasinb+isinacosb−i2sinasinb
化简后:
cos a cos b + sin a sin b + i ( sin a cos b − cos a sin b ) \cos a \cos b + \sin a \sin b + i(\sin a \cos b - \cos a \sin b) cosacosb+sinasinb+i(sinacosb−cosasinb)
左边根据欧拉公式为:
e i ( a − b ) = cos ( a − b ) + i sin ( a − b ) e^{i(a - b)} = \cos(a - b) + i\sin(a - b) ei(a−b)=cos(a−b)+isin(a−b)
比较实部和虚部,得:
{ cos ( a − b ) = cos a cos b + sin a sin b sin ( a − b ) = sin a cos b − cos a sin b \begin{cases} \cos(a - b) = \cos a \cos b + \sin a \sin b \\ \sin(a - b) = \sin a \cos b - \cos a \sin b \end{cases} {cos(a−b)=cosacosb+sinasinbsin(a−b)=sinacosb−cosasinb
口诀辅助记忆:
- 正弦和差:乘积符号相同( sin ( a ± b ) = sin a cos b ± cos a sin b \sin(a \pm b) = \sin a \cos b \pm \cos a \sin b sin(a±b)=sinacosb±cosasinb),谐音为:帅哥很帅符号同。
- 余弦和差:乘积符号相反( cos ( a ± b ) = cos a cos b ∓ sin a sin b \cos(a \pm b) = \cos a \cos b \mp \sin a \sin b cos(a±b)=cosacosb∓sinasinb),谐音为:哥哥帅帅符号异。
其他三角函数公式的证明
诱导公式可由和差公式推导,此处不再赘述。
结合 sin 2 α + cos 2 α = 1 \sin^2{\alpha} + \cos^2{\alpha} = 1 sin2α+cos2α=1,在和差公式中,当 α \alpha α 与 β \beta β 相等时可以推导出倍角公式。
将倍角公式中的 α \alpha α 换成 α 2 \frac{\alpha}{2} 2α 就可推导出降幂公式,两边同时开根号就变成了半角公式。
由半角公式又可推导出万能公式。
和差化积公式就是通过 α = α + β 2 + α − β 2 \alpha = \frac{\alpha + \beta}{2} + \frac{\alpha - \beta}{2} α=2α+β+2α−β 和 β = α + β 2 − α − β 2 \beta = \frac{\alpha + \beta}{2} - \frac{\alpha - \beta}{2} β=2α+β−2α−β 结合和差公式推导的,其逆过程就是积化和差公式。
例如,
sin α + sin β = sin ( α + β 2 + α − β 2 ) + sin ( α + β 2 − α − β 2 ) = 2 sin α + β 2 cos α − β 2 \sin{\alpha} + \sin{\beta} = \sin{\left( \frac{\alpha + \beta}{2} + \frac{\alpha - \beta}{2} \right)} + \sin{\left( \frac{\alpha + \beta}{2} - \frac{\alpha - \beta}{2} \right)} = 2\sin{\frac{\alpha + \beta}{2}}\cos{\frac{\alpha - \beta}{2}} sinα+sinβ=sin(2α+β+2α−β)+sin(2α+β−2α−β)=2sin2α+βcos2α−β
令
c = α + β 2 , b = α − β 2 c = \frac{\alpha + \beta}{2}, \quad b = \frac{\alpha - \beta}{2} c=2α+β,b=2α−β
解得
α = c + b , β = c − b \alpha = c + b, \quad \beta = c - b α=c+b,β=c−b
代入上式得
sin c cos b = 1 2 [ sin ( c + b ) + sin ( c − b ) ] \sin{c} \cos{b} = \frac{1}{2} [\sin{(c + b)} + \sin{(c - b)}] sinccosb=21[sin(c+b)+sin(c−b)]
1 + tan 2 α = sec 2 α 1 + \tan^2{\alpha} = \sec^2{\alpha} 1+tan2α=sec2α
与
1 + cot 2 α = csc 2 α 1 + \cot^2{\alpha} = \csc^2{\alpha} 1+cot2α=csc2α
是通过 sin 2 α + cos 2 α = 1 \sin^2{\alpha} + \cos^2{\alpha} = 1 sin2α+cos2α=1, sec α = 1 cos α \sec{\alpha} = \frac{1}{\cos{\alpha}} secα=cosα1 和 csc α = 1 sin α \csc{\alpha} = \frac{1}{\sin{\alpha}} cscα=sinα1 来证明的。
反三角函数常见公式的证明
反函数的重要性质:
f ( f − 1 ( x ) ) = x 对 f − 1 ( x ) 的定义域有效 f(f^{-1}(x)) = x \quad \text{对} \ f^{-1}(x) \ \text{的定义域有效} f(f−1(x))=x对 f−1(x) 的定义域有效
f − 1 ( f ( x ) ) = x 对 f ( x ) 的定义域有效 f^{-1}(f(x)) = x \quad \text{对} \ f(x) \ \text{的定义域有效} f−1(f(x))=x对 f(x) 的定义域有效
反三角函数的公式是通过反函数的定义与性质,结合三角函数的恒等式、导数规则及几何意义推导而来的,但需严格考虑定义域和主值范围的限制。
一、基础恒等式(互为反函数)
- 反正弦与正弦
sin ( arcsin x ) = x ( x ∈ [ − 1 , 1 ] ) \sin(\arcsin x) = x \quad (x \in [-1, 1]) sin(arcsinx)=x(x∈[−1,1])
arcsin ( sin x ) = x ( x ∈ [ − π / 2 , π / 2 ] ) \arcsin(\sin x) = x \quad (x \in [-\pi/2, \pi/2]) arcsin(sinx)=x(x∈[−π/2,π/2])
- 反余弦与余弦
cos ( arccos x ) = x ( x ∈ [ − 1 , 1 ] ) \cos(\arccos x) = x \quad (x \in [-1, 1]) cos(arccosx)=x(x∈[−1,1])
arccos ( cos x ) = x ( x ∈ [ 0 , π ] ) \arccos(\cos x) = x \quad (x \in [0, \pi]) arccos(cosx)=x(x∈[0,π])
- 反正切与正切
tan ( arctan x ) = x ( x ∈ R ) \tan(\arctan x) = x \quad (x \in \mathbb{R}) tan(arctanx)=x(x∈R)
arctan ( tan x ) = x ( x ∈ ( − π / 2 , π / 2 ) ) \arctan(\tan x) = x \quad (x \in (-\pi/2, \pi/2)) arctan(tanx)=x(x∈(−π/2,π/2))
二、角度和与差恒等式
- 互余关系
arcsin x + arccos x = π 2 ( x ∈ [ − 1 , 1 ] ) \arcsin x + \arccos x = \frac{\pi}{2} \quad (x \in [-1, 1]) arcsinx+arccosx=2π(x∈[−1,1])
arctan x + arccot x = π 2 ( x ∈ R ) \arctan x + \text{arccot} \, x = \frac{\pi}{2} \quad (x \in \mathbb{R}) arctanx+arccotx=2π(x∈R)
口诀:互余角,相加 π / 2 \pi/2 π/2。
证明:设 θ = arcsin x \theta = \arcsin x θ=arcsinx,其中 x ∈ [ − 1 , 1 ] x \in [-1, 1] x∈[−1,1]。根据定义:
sin θ = x 且 θ ∈ [ − π 2 , π 2 ] \sin\theta = x \quad \text{且} \quad \theta \in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right] sinθ=x且θ∈[−2π,2π]
由三角恒等式 sin θ = cos ( π 2 − θ ) \sin\theta = \cos\left(\frac{\pi}{2} - \theta\right) sinθ=cos(2π−θ),得:
x = cos ( π 2 − θ ) x = \cos\left(\frac{\pi}{2} - \theta\right) x=cos(2π−θ)
由于 π 2 − θ ∈ [ 0 , π ] \frac{\pi}{2} - \theta \in [0, \pi] 2π−θ∈[0,π](反余弦函数的定义域),根据反余弦定义:
arccos x = π 2 − θ \arccos x = \frac{\pi}{2} - \theta arccosx=2π−θ
合并表达式:
arcsin x + arccos x = θ + ( π 2 − θ ) = π 2 \arcsin x + \arccos x = \theta + \left(\frac{\pi}{2} - \theta\right) = \frac{\pi}{2} arcsinx+arccosx=θ+(2π−θ)=2π
PS:在这里提一下, sin ( arccos x ) \sin(\arccos x) sin(arccosx) 可以通过上式转换成 sin ( π − arcsin x ) \sin(\pi - \arcsin x) sin(π−arcsinx)。
- 和角公式
arcsin a + arcsin b = arcsin ( a 1 − b 2 + b 1 − a 2 ) 当 a , b ≥ 0 且 a 2 + b 2 ≤ 1 时 \arcsin a + \arcsin b = \arcsin\left(a\sqrt{1 - b^2} + b\sqrt{1 - a^2}\right) \quad \text{当 } a, b \geq 0 \text{ 且 } a^2 + b^2 \leq 1 \text{ 时} arcsina+arcsinb=arcsin(a1−b2+b1−a2)当 a,b≥0 且 a2+b2≤1 时
证明:令 a = sin A a = \sin A a=sinA, b = sin B b = \sin B b=sinB。则原等式右边为
arcsin ( sin A cos B + cos A sin B ) = arcsin ( sin ( A + B ) ) = A + B \arcsin(\sin A \cos B + \cos A \sin B) = \arcsin(\sin(A + B)) = A + B arcsin(sinAcosB+cosAsinB)=arcsin(sin(A+B))=A+B
而当满足条件时,上式即等于原等式左边。
arctan a + arctan b = arctan ( a + b 1 − a b ) (当 a b < 1 时) \arctan a + \arctan b = \arctan\left(\frac{a + b}{1 - ab}\right) \quad \text{(当 } ab < 1 \text{ 时)} arctana+arctanb=arctan(1−aba+b)(当 ab<1 时)
三、与原三角函数的关系
- 反余弦的正弦表达式
sin ( arccos x ) = 1 − x 2 ( x ∈ [ − 1 , 1 ] ) \sin(\arccos x) = \sqrt{1 - x^2} \quad (x \in [-1, 1]) sin(arccosx)=1−x2(x∈[−1,1])
证明:令 t = arccos x ∈ [ 0 , π ] t = \arccos x \in [0, \pi] t=arccosx∈[0,π],则 x = cos t x = \cos t x=cost, sin t ≥ 0 \sin t \geq 0 sint≥0。
又 sin 2 α + cos 2 α = 1 \sin^2{\alpha} + \cos^2{\alpha} = 1 sin2α+cos2α=1,因此
sin t = 1 − x 2 \sin t = \sqrt{1 - x^2} sint=1−x2
即
sin ( arccos x ) = 1 − x 2 ( x ∈ [ − 1 , 1 ] ) \sin(\arccos x) = \sqrt{1 - x^2} \quad (x \in [-1, 1]) sin(arccosx)=1−x2(x∈[−1,1])
- 反正弦的余弦表达式
cos ( arcsin x ) = 1 − x 2 ( x ∈ [ − 1 , 1 ] ) \cos(\arcsin x) = \sqrt{1 - x^2} \quad (x \in [-1, 1]) cos(arcsinx)=1−x2(x∈[−1,1])
- 反正切的正弦与余弦
sin ( arctan x ) = x 1 + x 2 \sin(\arctan x) = \frac{x}{\sqrt{1 + x^2}} sin(arctanx)=1+x2x
cos ( arctan x ) = 1 1 + x 2 \cos(\arctan x) = \frac{1}{\sqrt{1 + x^2}} cos(arctanx)=1+x21
证明:设 θ = arctan x \theta = \arctan x θ=arctanx,其中 x ∈ R x \in \mathbb{R} x∈R。根据定义:
tan θ = x 且 θ ∈ ( − π 2 , π 2 ) \tan\theta = x \quad \text{且} \quad \theta \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) tanθ=x且θ∈(−2π,2π)
由 1 + tan 2 θ = sec 2 θ 1 + \tan^2\theta = \sec^2\theta 1+tan2θ=sec2θ,代入 tan θ = x \tan\theta = x tanθ=x:
1 + x 2 = sec 2 θ ⟹ cos θ = 1 sec θ = 1 1 + x 2 1 + x^2 = \sec^2\theta \implies \cos\theta = \frac{1}{\sec\theta} = \frac{1}{\sqrt{1 + x^2}} 1+x2=sec2θ⟹cosθ=secθ1=1+x21
由 sin θ = tan θ ⋅ cos θ \sin\theta = \tan\theta \cdot \cos\theta sinθ=tanθ⋅cosθ,代入 tan θ = x \tan\theta = x tanθ=x 和 cos θ = 1 1 + x 2 \cos\theta = \frac{1}{\sqrt{1 + x^2}} cosθ=1+x21:
sin θ = x ⋅ 1 1 + x 2 = x 1 + x 2 \sin\theta = x \cdot \frac{1}{\sqrt{1 + x^2}} = \frac{x}{\sqrt{1 + x^2}} sinθ=x⋅1+x21=1+x2x
四、反函数间的转换
- 反余弦与反正弦
arccos x = arcsin ( 1 − x 2 ) ( x ∈ [ 0 , 1 ] ) \arccos x = \arcsin\left(\sqrt{1 - x^2}\right) \quad (x \in [0, 1]) arccosx=arcsin(1−x2)(x∈[0,1])
证明:该式其实就是通过反余弦的正弦表达式转换过来的。
- 反余切与反正切
arccot x = arctan ( 1 x ) ( x > 0 ) \text{arccot} \, x = \arctan\left(\frac{1}{x}\right) \quad (x > 0) arccotx=arctan(x1)(x>0)
五、三角函数与反三角函数作用
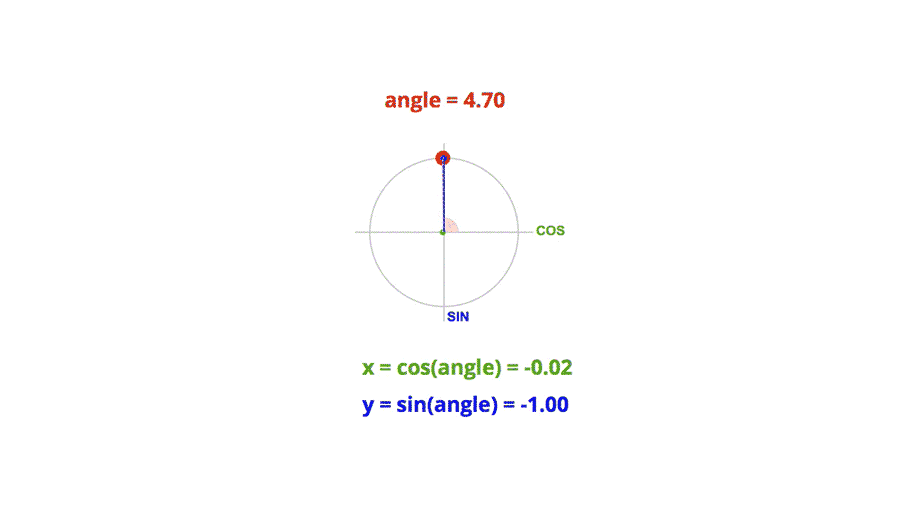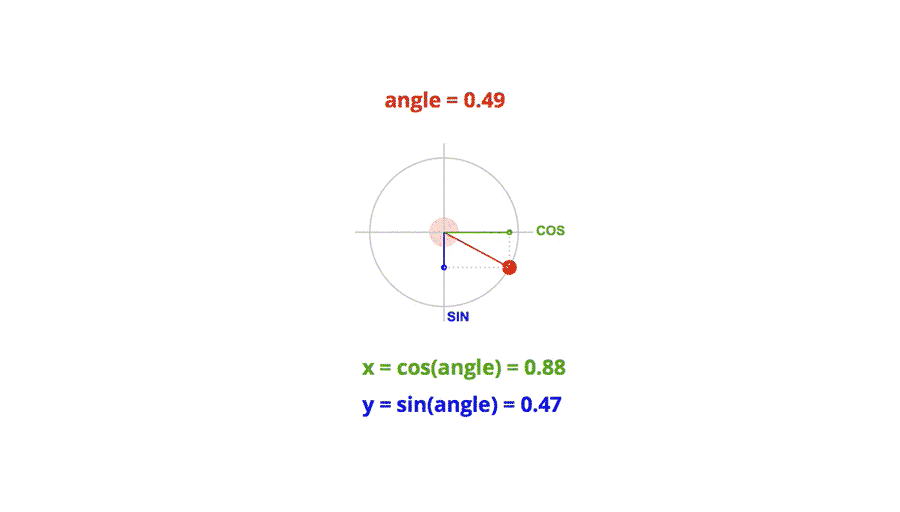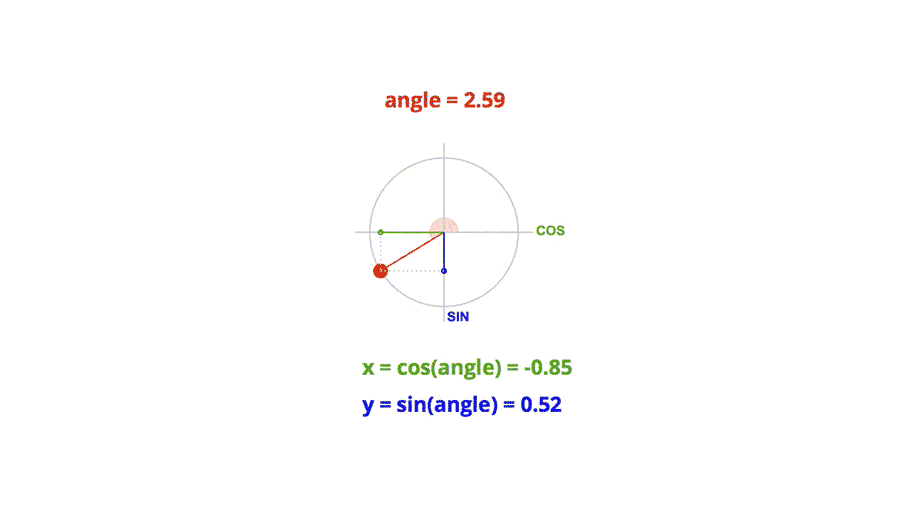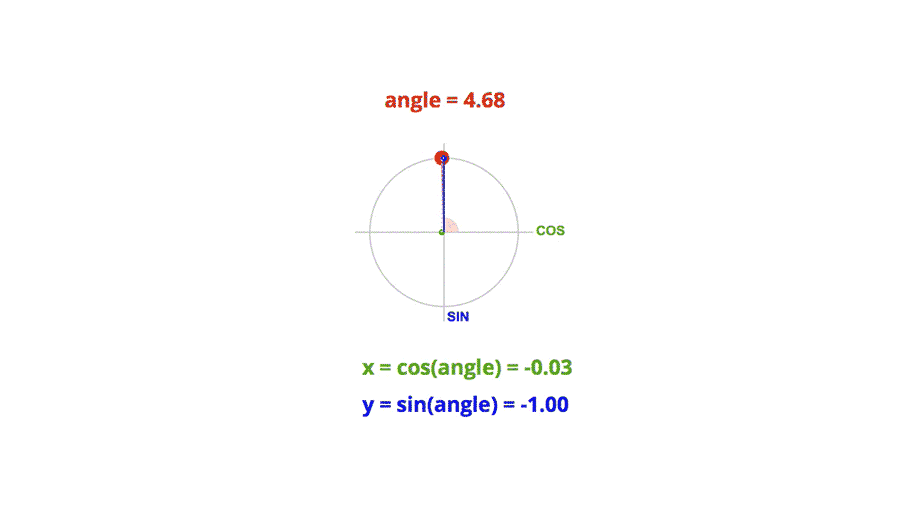
三角函数:在单位圆中,通过给定圆心角 θ \theta θ,求出对应点的坐标分量 ( cos θ , sin θ ) (\cos\theta, \sin\theta) (cosθ,sinθ)。
反三角函数:给定单位圆上点的坐标 ( x , y ) (x, y) (x,y),求出对应的圆心角 θ \theta θ,结果限制在主值范围内(例如, arcsin x \arcsin x arcsinx 的主值范围是 [ − π 2 , π 2 ] [- \frac{\pi}{2}, \frac{\pi}{2}] [−2π,2π], arccos x \arccos x arccosx 的主值范围是 [ 0 , π ] [0, \pi] [0,π])。
总结
三角函数是圆心角到坐标分量的映射;反三角函数是坐标分量到圆心角的映射,且结果通常受到主值范围的限制。
三角函数的另外三个伙伴—— cot \cot cot, sec \sec sec, csc \csc csc
strategist 发布于 2020-07-21 19:03
一、前言
本文介绍高考不考、大学必学的基础知识,属于初高中与大学数学的衔接内容,目标读者为已参加高考的学生。鉴于网络资料零散,本文予以整合,力求通俗讲解,帮助更多学生掌握——这并非拔高内容,而是必备知识。因属初等数学范畴,将投稿至初等数学专栏。
| 符号 | 英文读音(IPA) | 中文名称 |
|---|---|---|
| sin \sin sin | /saɪn/ | 正弦 |
| cos \cos cos | /koʊsaɪn/ 或 /kəʊsaɪn/ | 余弦 |
| tan \tan tan | /tændʒənt/ 或 /tæn/ | 正切 |
| cot \cot cot | /koʊˈtændʒənt/ 或 /koʊˈtæn/ | 余切 |
| sec \sec sec | /siːkənt/ 或 /siːk/ | 正割 |
| csc \csc csc | /koʊˈsiːkənt/ 或 /koʊˈsiːk/ | 余割 |
二、知识讲解
1. 认识另外三个三角函数
- cot \cot cot(余切):与 tan \tan tan 互为倒数, cot x = 1 tan x \cot x=\dfrac{1}{\tan x} cotx=tanx1;在直角三角形中, cot = 邻边 对边 \cot=\dfrac{\text{邻边}}{\text{对边}} cot=对边邻边。
- sec \sec sec(正割):与 cos \cos cos 互为倒数, sec x = 1 cos x \sec x=\dfrac{1}{\cos x} secx=cosx1;在直角三角形中, sec = 斜边 邻边 \sec=\dfrac{\text{斜边}}{\text{邻边}} sec=邻边斜边。
- csc \csc csc(余割):与 sin \sin sin 互为倒数, csc x = 1 sin x \csc x=\dfrac{1}{\sin x} cscx=sinx1;在直角三角形中, csc = 斜边 对边 \csc=\dfrac{\text{斜边}}{\text{对边}} csc=对边斜边。
2. 函数图像绘制与分析
初学者应自主探究绘图,亲自动手可加深理解并锻炼探究能力。
- y = sec x y=\sec x y=secx:结合 sec \sec sec 与 cos \cos cos 互为倒数的关系找点,再连线绘制。其图像每半个周期形态类似“大铲子”。
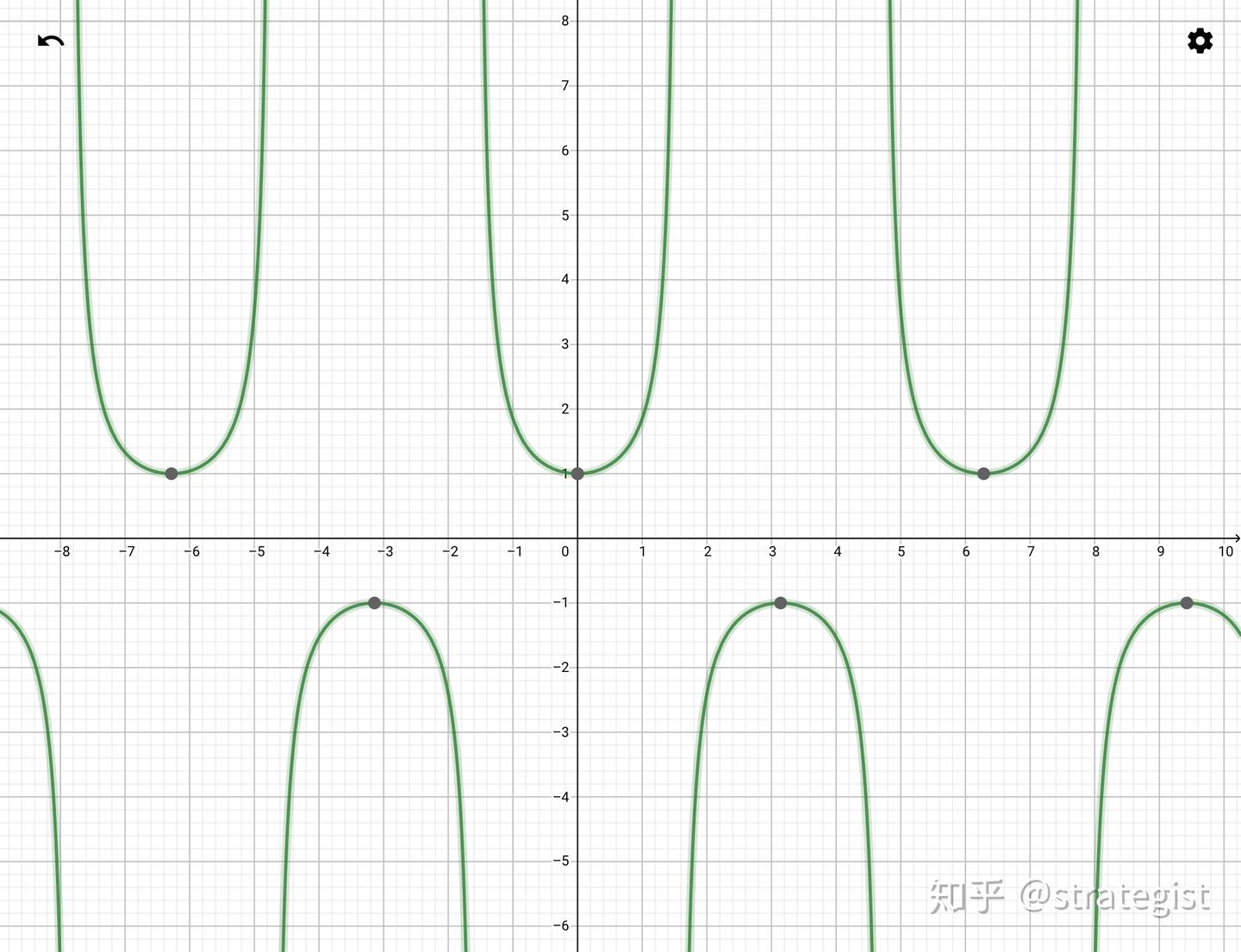
图 1
y
=
sec
x
y=\sec x
y=secx 图像
放大后可观察其细节特征:
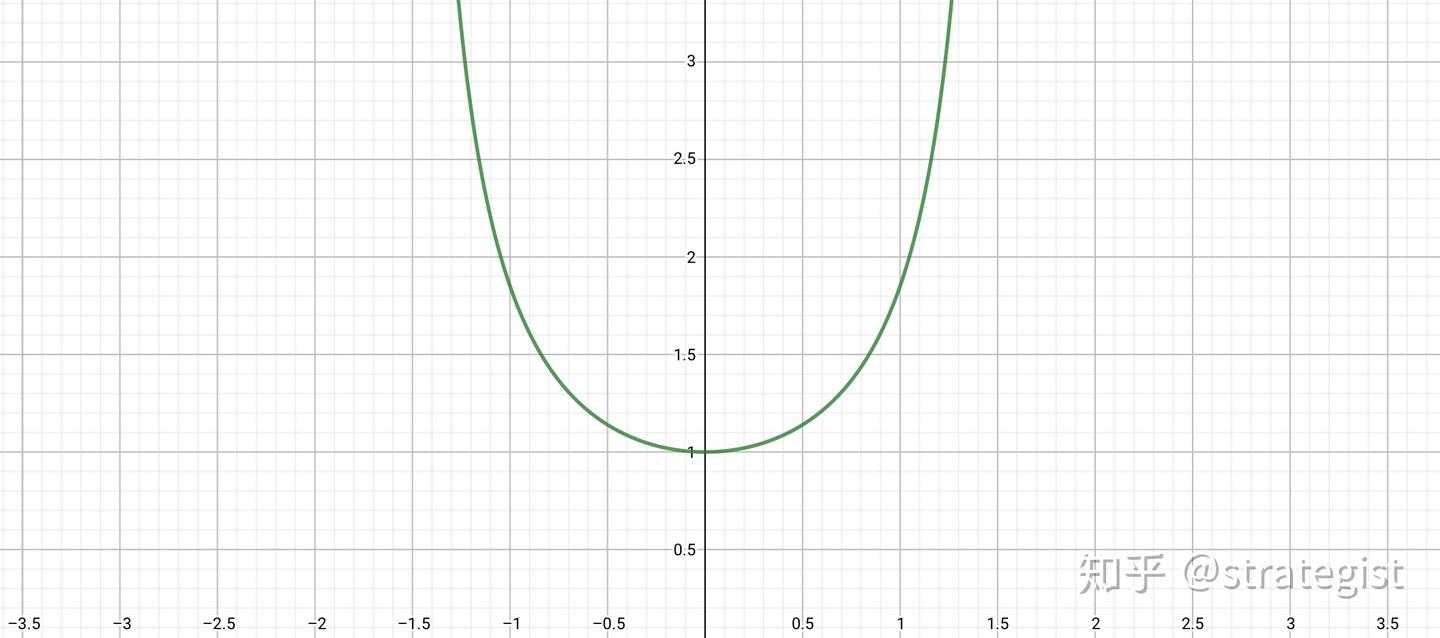
图 2
y
=
sec
x
y=\sec x
y=secx 一个周期内的一支
结合 y = cos x y=\cos x y=cosx 图像可辅助理解:
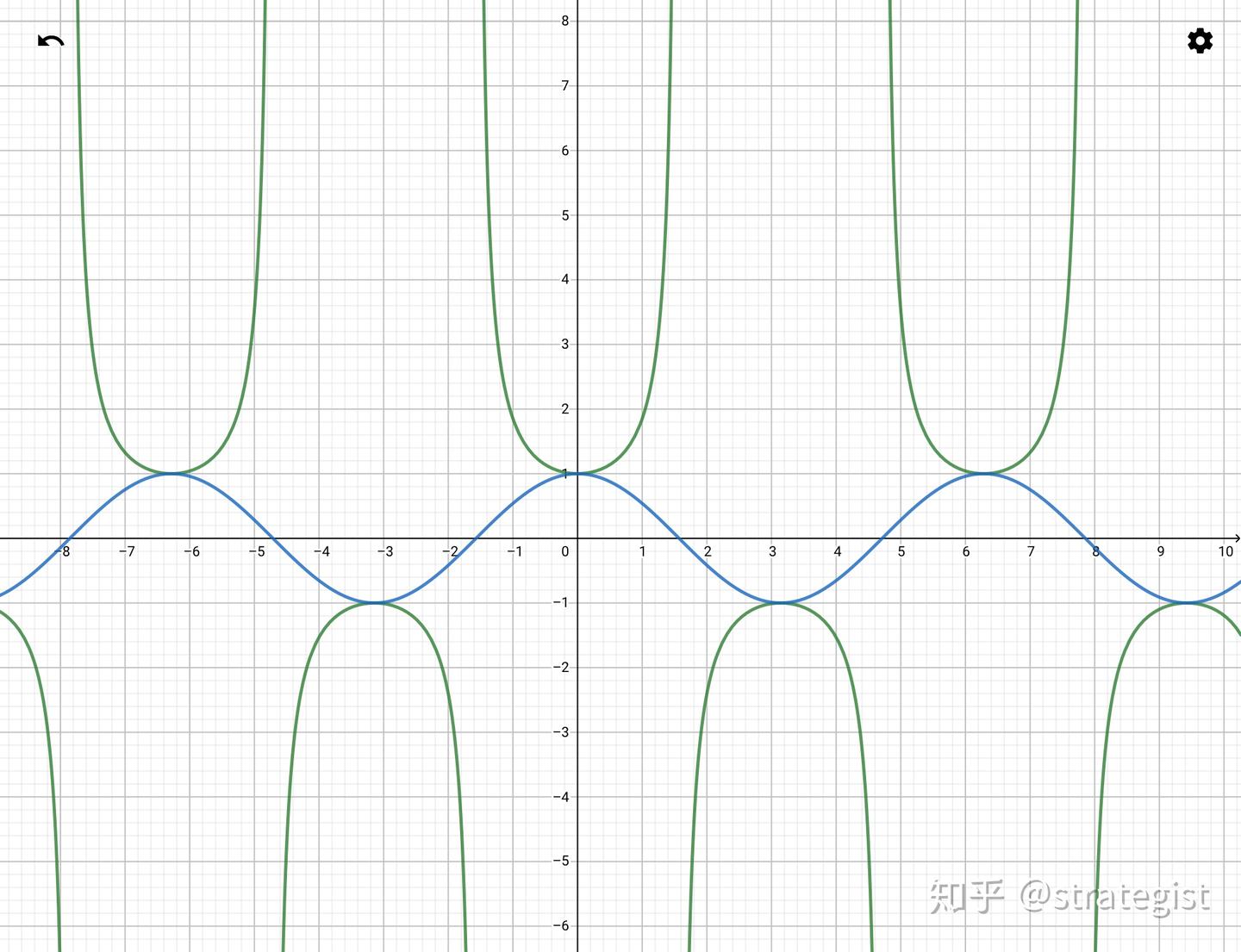
图 3
y
=
cos
x
y=\cos x
y=cosx 和
y
=
sec
x
y=\sec x
y=secx 对比
- y = csc x y=\csc x y=cscx:研究方法同 y = sec x y=\sec x y=secx,可结合 y = sin x y=\sin x y=sinx 图像(二者互为倒数):
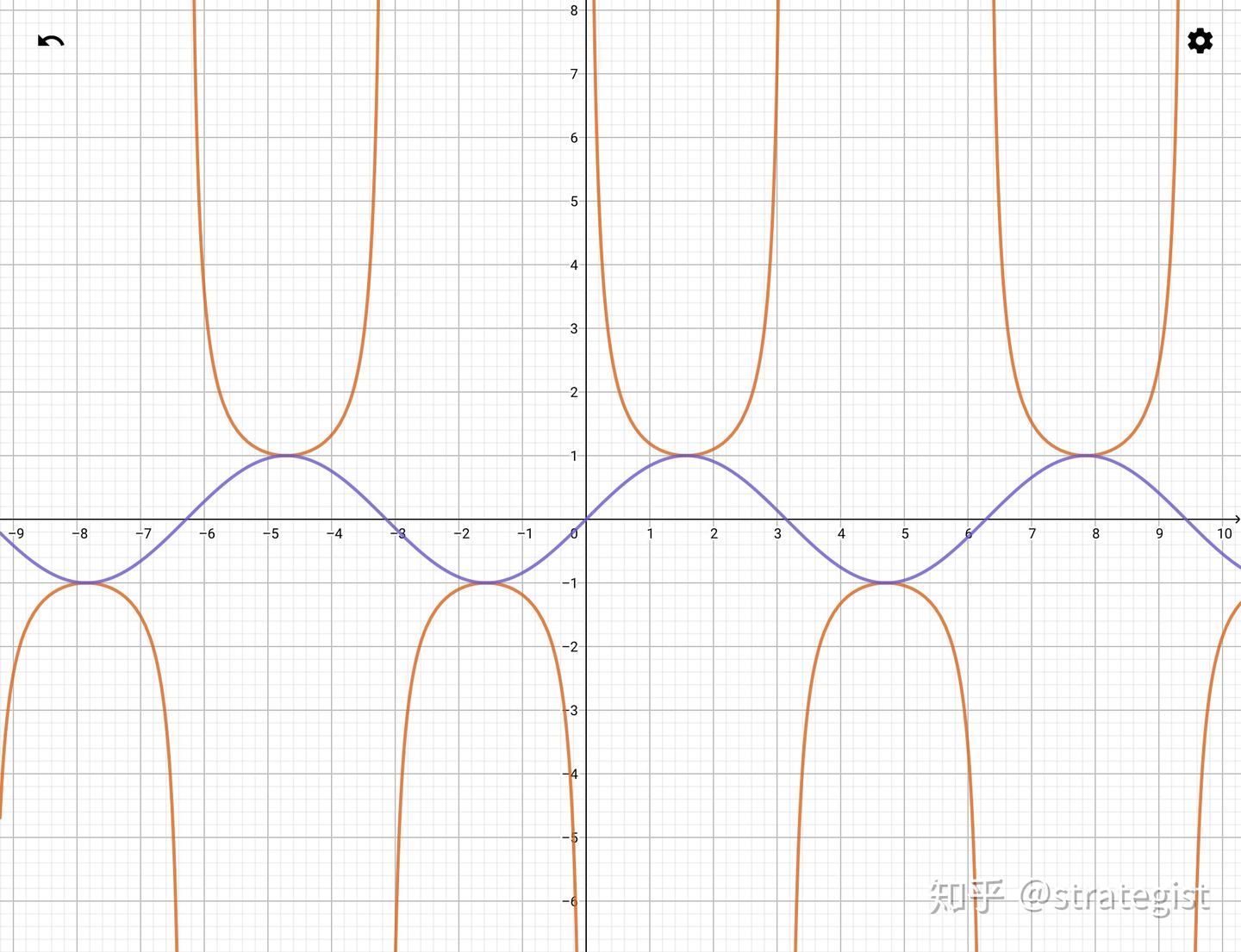
图 4
y
=
sin
x
y=\sin x
y=sinx 和
y
=
csc
x
y=\csc x
y=cscx 对比
-
周期性:由图 3、4 可知, sec \sec sec、 csc \csc csc 最小正周期为 2 π 2\pi 2π;因 tan \tan tan 与 cot \cot cot 互为倒数,且 tan \tan tan 周期为 π \pi π,故 cot x \cot x cotx 最小正周期为 π \pi π。
-
y = cot x y=\cot x y=cotx:通过找特殊点连线绘制,图像如下:
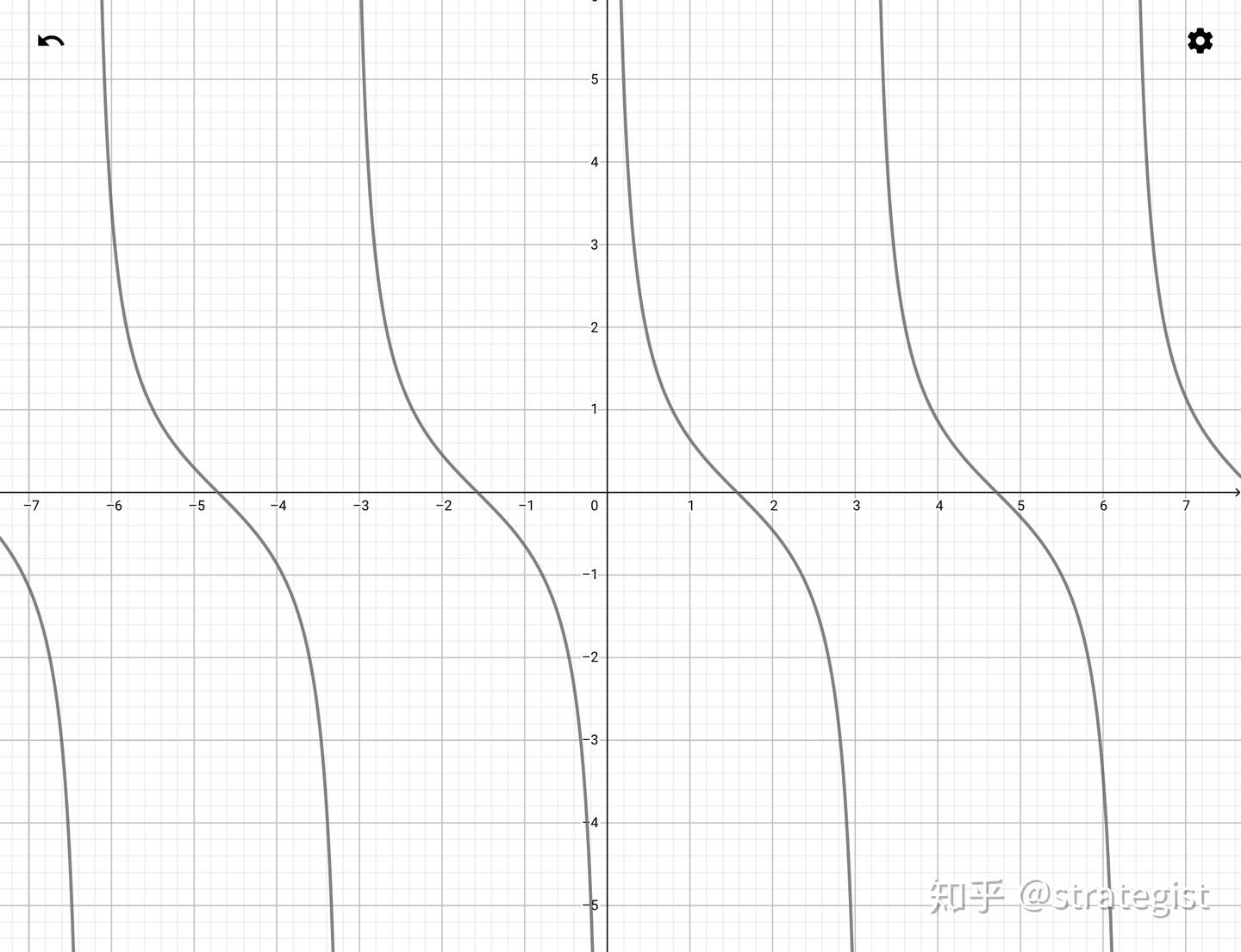
图 5
y
=
cot
x
y=\cot x
y=cotx 图像
绘制图像后,建议从定义域、值域、周期性、奇偶性、单调性、对称性六个方面研究函数性质。
3. 六边形记忆法
该方法可有效总结相关公式,规律如下:
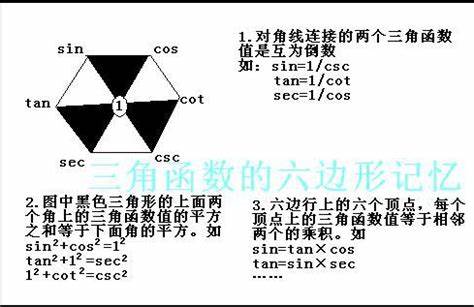
图 6 六边形记忆法
-
宏观规律:左半为“正”函数,右半为“余”函数;横向分“弦”(上)、“切”(中)、“割”(下),可标“正余弦切割”辅助记忆。
-
微观规律(邻、间、对):可类比化学里的二甲苯
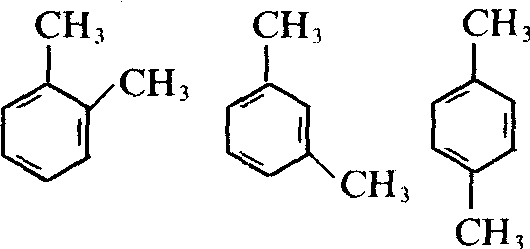
-
对位: tan \tan tan 与 cot \cot cot 互为倒数(共三对)。
-
邻位: sin \sin sin 与 cos \cos cos 满足平方和关系 sin 2 + cos 2 = 1 \sin^{2}+\cos^{2}=1 sin2+cos2=1,类似有 tan 2 + 1 = sec 2 \tan^{2}+1=\sec^{2} tan2+1=sec2, cot 2 + 1 = csc 2 \cot^{2}+1=\csc^{2} cot2+1=csc2(可类比杨辉三角“两肩得下方”记忆)。
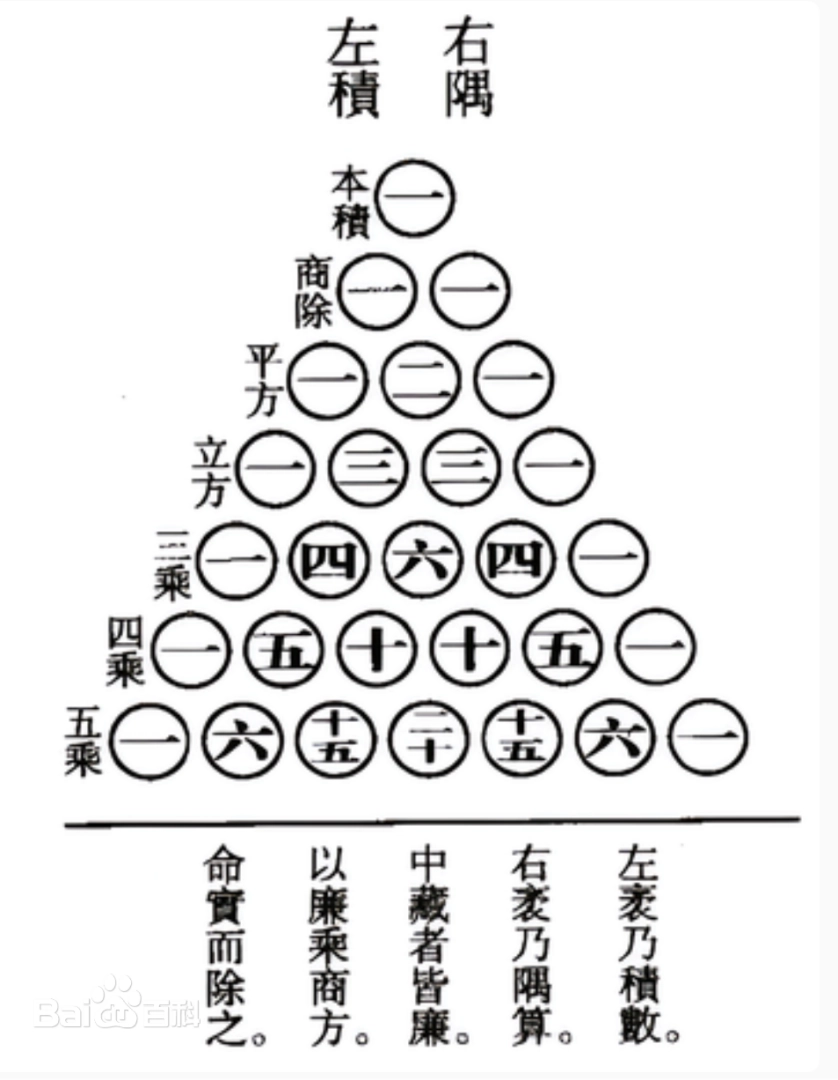
图 7 杨辉三角
- 间位: sec = tan ⋅ csc \sec=\tan\cdot\csc sec=tan⋅csc,即每个顶点函数等于相邻两函数乘积。
掌握上述规律后,可推导同角三角函数基本关系式(如图 8):

图 8 同角三角函数的基本关系式
三、总结
本文讲解了 cot \cot cot、 sec \sec sec、 csc \csc csc 的图像及常用公式,这些是三角函数的必备补充内容。反三角函数未涉及,因笔者水平有限,未能深入讲解,建议有能力的读者进一步探究。
via:
-
数学 三角函数 sin 正弦、cos 余弦、tan 正切、cot 余切、sec 正割、csc 余割 简介_sin cos tan cot sec csc-优快云博客
https://blog.youkuaiyun.com/whatday/article/details/126393819 -
三角函数及其常用公式-优快云博客
https://blog.youkuaiyun.com/mtc1170824134/article/details/139361968
参考资料- 反三角函数和差角公式
https://www.zhihu.com/question/339027658 - 论语·述而篇
https://www.gushiwen.cn/mingju/juv.aspx?id=6398c3196595 - 两角和差公式
https://www.geogebra.org/classic/excbxdxv - 这些三角函数的名称是怎么来的?
https://www.bilibili.com/video/BV1GY4y1m7bF - 数学大悲咒-三角函数之歌
https://www.bilibili.com/video/BV1McbFe5EkR - 三角函数之歌《trigonometric functions》
https://www.bilibili.com/video/BV13f4y127mM - 三角函数-和角化积-公式 动画演示推导过程
https://www.bilibili.com/video/BV17UhLe5Ebn - 三角函数天才图解!一图牢记六大三角函数和差公式
https://www.bilibili.com/video/BV1Mw41177y7 - 对于arcsinx+arccosx=π/2(x∈[-1,1])的证明
https://www.bilibili.com/opus/686105280453279812 - 百度百科-三角函数
https://baike.baidu.com/item/三角函数/1652457 - 正弦、余弦和正切的图
https://www.shuxuele.com/algebra/trig-sin-cos-tan-graphs.html - 戈小戈–三角函数与反三角函数的定义、图像、导数(推导)完整版
https://www.cnblogs.com/wsgxg/p/16739439.html - Latex-六个三角函数的图像
https://www.latexstudio.net/index.php/index/details/index/mid/2114.html
- 反三角函数和差角公式
-
常用三角函数公式与反三角函数公式的证明_三角函数公式及证明-优快云博客
https://blog.youkuaiyun.com/qq_74204532/article/details/146611992 -
三角函数的另外三个伙伴—cot,sec,csc - 知乎
https://zhuanlan.zhihu.com/p/162297688





















 20万+
20万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








