Pytorch深入浅出（四）之nn网络层（池化、线性、激活函数）

三、池化

1.直观理解
如果说卷积层是“特征提取”，那么池化层就是特征降维（下采样）。

• 核心目的： 减少数据量（参数量），降低计算成本，同时防止过拟合。它能保留最显著的特征，并赋予网络一定的平移不变性。
• 池化运算： 同样有一个“滑动窗口”在输入图像上滑动，但它不进行乘加运算，而是进行统计运算。
  • 最大池化 (Max Pooling)：选窗口内最大的值。提取纹理、边缘等最显著特征（最常用）。
  • 平均池化 (Avg Pooling)：算窗口内平均值。保留背景信息。
• 池化维度：与卷积类似，也分为1D、2D、3D池化。

💡 关键理解：通道独立性
与卷积层不同，池化层的运算是独立作用于每一个通道的。

• 输入： 假设输入是 RGB 图像（3通道）。
• 运算： 池化核在 R 通道上操作得到 R 通道的输出，在 G 通道上操作得到 G 通道的输出。不会像卷积那样将不同通道的结果相加。
• 输出： 池化操作永远不会改变通道数（$C_{out}=C_{in}$），只改变图像的宽 ($W$) 和高 ($H$)。

2.nn.MaxPool2d核心参数详解
PyTorch 中，MaxPool2d 是最常用的二维池化类，其参数如下：

参数名	含义	详细说明
kernel_size	池化核尺寸	窗口的大小。如 2 代表 $2\times 2$ 区域
stride	步长	注意： 默认值是 kernel_size。这与卷积不同（卷积默认为1）。即默认情况下窗口移动是不重叠的
padding	填充	在边缘填充的值（通常不填充）。用于处理无法整除的情况
dilation	空洞/扩张	控制窗口元素间的步幅（极少用到）
return_indices	返回索引	默认为 False。如果在后续需要做最大反池化（MaxUnpool2d）时，需要设为 True
ceil_mode	向上取整	默认为 False（向下取整）。计算输出尺寸时，若无法除尽，True 则保留不足的边，False 则丢弃

注意：对于 kernel_size 和 stride，同样支持 int 或 tuple 输入，规则与卷积层一致（第一个数对应 H，第二个数对应 W）。

3.池化参数对输出尺寸的影响

• kernel_size、stride、padding 等参数会改变特征图的尺寸
• 池化层不改变通道数
• 池化层没有可学习的参数（没有 weight 和 bias）
  计算公式与卷积层基本一致：

import torch
import torch.nn as nn

# 模拟特征图：Batch=1, Channel=64, H=32, W=32
x = torch.randn(1, 64, 32, 32)

# 【情况1】尺寸减半 (最经典用法)
# kernel_size=2, 默认 stride=2
pool_half = nn.MaxPool2d(kernel_size=2)
print(f"{pool_half(x).shape}")   # torch.Size([1, 64, 16, 16])

# 【情况2】尺寸非整除 (ceil_mode的影响)
# 输入为32，kernel=3, stride=2。 (32-3)/2 + 1 = 15.5
pool_floor = nn.MaxPool2d(3, stride=2, ceil_mode=False) # 默认向下取整
pool_ceil  = nn.MaxPool2d(3, stride=2, ceil_mode=True)  # 向上取整

print(f"{pool_floor(x).shape}")  # torch.Size([1, 64, 15, 15]) -> 丢弃边缘
print(f"{pool_ceil(x).shape}")   # torch.Size([1, 64, 16, 16]) -> 保留边缘

4.池化再理解
用代码可视化池化层的“马赛克”效果（降采样）：

import torch
import torch.nn as nn
from PIL import Image
from torchvision import transforms
import matplotlib.pyplot as plt

# 1. 读取并处理图片
image_path = r"D:/Photos\desktop photos/t01662406687cf7219b.jpg"
img = Image.open(image_path).convert('RGB')
transform = transforms.ToTensor()
img_tensor = transform(img).unsqueeze(0) # 增加 Batch 维度 -> (1, 3, H, W)

# 2. 定义最大池化层
# 使用 8x8 的核，步长也为 8，相当于把每 8x8 个像素合并为一个
pool = nn.MaxPool2d(kernel_size=8, stride=8)

# 3. 前向传播
img_pool = pool(img_tensor)

# 4. 可视化对比
plt.figure(figsize=(10,6))
plt.subplot(1,2,1)
plt.title("Original")
plt.imshow(img)
plt.axis('off')
plt.subplot(1,2,2)
plt.title("Max Pooling (8x8)")
# 将 Tensor 转回 numpy 并调整维度顺序 (C,H,W -> H,W,C) 以显示
out_img = img_pool.squeeze().permute(1, 2, 0).numpy()
plt.imshow(out_img)
plt.axis('off')
plt.show()

右边的图像变“糊”了，出现了马赛克块，像素宽高变成了原来的 1/8。虽然细节丢失了，但图像的主体轮廓（如物体的位置、颜色概貌）依然保留。这就是池化层在降低运算量的同时，保留主要特征的直观体现。

四、全连接层

1.直观理解
线性层（Linear Layer），也常被称为全连接层（Fully Connected Layer, FC）。

• 全连接运算： 它是最基本的神经网络结构。本质上就是矩阵乘法。
• 连接方式： 这一层的每一个输出节点，都和上一层的每一个输入节点相连，然后加权汇总。
• 功能定位： 如果说卷积层负责“提取局部特征”，那么线性层通常负责“综合全局信息”。它常位于网络的末端，用于将提取到的特征映射到最终的分类结果（如10分类）或回归数值上。
  
  💡 关键理解：维度匹配
  线性层对输入数据的形状非常挑剔。它通常只接受二维张量 (Batch_Size, Input_Features)。 因此，在卷积层和线性层之间，通常需要一个 “展平（Flatten）” 操作，将多维的特征图（如 C×H×W）拉直成一条长向量。

2.nn.Linear核心参数详解
在 PyTorch 中，Linear 是实现线性变换的类，参数非常简洁：

参数名	含义	详细说明
in_features	输入特征数	输入向量的大小。必须与输入张量的最后一个维度一致
out_features	输出特征数	输出向量的大小。通常对应分类任务的类别数，或隐藏层的神经元数量
bias	偏置	默认为 True。给线性变换加上一个可学习的偏置项 $b$

注意：计算量的差异——虽然参数看起来少，但线性层的参数量往往是巨大的。例如输入是 $512\times 7\times 7$ 的特征图，输出是 1000 类。 in_features = $512\times 7\times 7=25088$ out_features = $1000$ 参数量 = $25088\times 1000\approx 2500$ 万个参数！这也是现代网络尽量减少全连接层使用的原因。

3.线性层参数对输出尺寸的影响

• in_features 和 out_features 直接决定了输入和输出张量的形状。
• 线性层会改变数据的最后一个维度，通常不改变Batch Size。

公式非常简单：

$N$是Batch size，$\ast$表示任意维度，但通常就是二维的

import torch
import torch.nn as nn

# 模拟卷积层输出的特征图：Batch=16, Channel=3, H=2, W=2
# 总共特征点数 = 16*2*2 = 64
x = torch.randn(16, 3, 2, 2)

# 【步骤1】展平 (Flatten)
# 在传入 Linear 之前，必须把 (C, H, W) 拉平成 (C*H*W)
x_flatten = x.view(x.size(0), -1) 
print(f"展平后: {x_flatten.shape}") # torch.Size([16, 12])

# 【步骤2】线性变换
# 定义线性层：输入必须是8，输出想要映射到3个类别
linear_layer = nn.Linear(in_features=12, out_features=3)

# 前向传播
out = linear_layer(x_flatten)
print(f"线性层输出: {out.shape}")    # torch.Size([16, 3])

4.直观再理解
用一个具体的“图像分类”流程来体现线性层的作用，构建LeNet网络

class LeNet(nn.Module):
	def __init__(self, num_classes=10):
		super().__init__()
		self.net = nn.Sequential(
		nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=0),
		nn.Sigmoid(),
		nn.AvgPool2d(kernel_size=2, stride=2),
		nn.Sigmoid(),
		nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0),
		nn.Sigmoid(),
		nn.AvgPool2d(kernel_size=2, stride=2),
		nn.Flatten(),
		nn.Linear(16*4*4, 120),
		nn.Sigmoid(),
		nn.Linear(120, 84),
		nn.Sigmoid(),
		nn.Linear(84, num_classes)
		)

	def forward(self, x):
		return self.net(x)

	def summary(self, input_shape=(1, 1, 28, 28)):
		"""分析网络每一层的输出形状"""
		X = torch.rand(size=input_shape)
		print(f'{"Input":>15} output shape: \t{X.shape}')
		for layer in self.net:
			X = layer(X)
			print(f'{layer.__class__.__name__:>15} output shape: \t{X.shape}')

net = LeNet()
net.summary()

线性层在这里扮演了“决策者”的角色，它不关心像素在图片左上角还是右下角（空间信息在展平时丢失了），它只关心这些像素值的加权总和与最终类别的关系。

Input output shape: torch.Size([1, 1, 28, 28])
Conv2d output shape: torch.Size([1, 6, 24, 24])
Sigmoid output shape: torch.Size([1, 6, 24, 24])
AvgPool2d output shape: torch.Size([1, 6, 12, 12])
Conv2d output shape: torch.Size([1, 16, 8, 8])
Sigmoid output shape: torch.Size([1, 16, 8, 8])
AvgPool2d output shape: torch.Size([1, 16, 4, 4])
Flatten output shape: torch.Size([1, 256])
Linear output shape: torch.Size([1, 120])
Sigmoid output shape: torch.Size([1, 120])
Linear output shape: torch.Size([1, 84])
Sigmoid output shape: torch.Size([1, 84])
Linear output shape: torch.Size([1, 10])

五、激活函数层

1.直观理解
如果说卷积层和全连接层是在“计算”，那么激活函数层就是在“做决定”**。

• 生物学启发： 类似于人脑神经元的“点火”机制。神经元只有在接收到的刺激超过一定阈值时才会由抑制状态转为兴奋状态（输出信号），否则保持静默。
• 数学本质： 引入非线性因素。它对输入数据的每一个元素单独进行某种数学变换，不改变数据的形状，只改变数值。
• 作用： 如果没有激活函数，无论神经网络有多少层，最终都只是线性运算的叠加（矩阵相乘），这使得网络无法拟合复杂的曲线（如异或问题、复杂的图像分类）。

💡 关键理解：为什么要非线性？
很多初学者不理解为什么必须加这一层。假设我们有两层网络，没有激活函数：

$$Output=W_2(W_{1}x+b_1)+b_2=(W_2{W}_1)x+(W_2{b}_1+b_2)=W^{\prime }x+b^{\prime }$$
你会发现，两层线性网络坍缩成了一层。
只有引入了非线性激活函数 $\sigma$，网络变成了 $W_2(\sigma (W_{1}x+b_1))+b_2$，这种结构才能逼近任意复杂的函数，这就是深度学习强大的根源。

2.常见激活函数及参数详解
在 PyTorch 中，激活函数同样继承自 nn.Module。以下是几种最常用的激活函数：

参数名	公式	特点与适用场景
nn.ReLU	$y=\max (0,x)$	最常用。计算快，解决了梯度消失问题。负数部分直接为0（死区）
nn.Sigmoid	$y=\frac{1}{1+e^{-x}}$	输出在 $(0,1)$ 之间。常用于二分类的输出层。容易导致梯度消失，隐藏层现已少用
nn.Tanh	$y=\frac{e^x-e^{-x}}{e^x+e^{-x}}$	输出在 $(-1,1)$ 之间。零均值化，优于 Sigmoid，但仍有梯度消失风险
nn.LeakyReLU	$y=\max (\alpha x,x)$	给负数部分一个很小的斜率 $\alpha$，避免神经元彻底“死亡”
nn.Softmax	$\frac{e^{x_i}}{\sum e^{x_j}}$	将输出转化为概率分布（和为1）。用于多分类任务的输出层

注意：原地操作 (In-place Operation)：在 nn.ReLU(inplace=True) 中，inplace=True 意味着直接在输入内存上修改数据，不创建新的输出张量。这对于显存有限的大模型训练非常有用，可以节省大量显存。

3.直观再理解
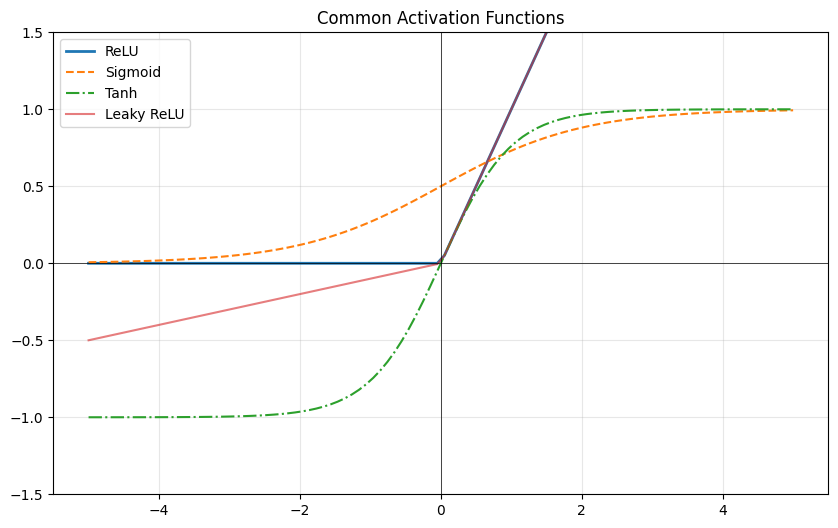
通过绘制函数图像，直观感受它们是如何改变数据的数值分布的：

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
  
# 创建一个从 -5 到 5 的输入数据
x = torch.linspace(-5, 5, 100)
  
# 实例化激活函数
relu = nn.ReLU()
sigmoid = nn.Sigmoid()
tanh = nn.Tanh()
leaky_relu = nn.LeakyReLU(negative_slope=0.1)
  
# 绘图
plt.figure(figsize=(10, 6))
plt.plot(x.numpy(), relu(x).numpy(), label='ReLU', linewidth=2)
plt.plot(x.numpy(), sigmoid(x).numpy(), label='Sigmoid', linestyle='--')
plt.plot(x.numpy(), tanh(x).numpy(), label='Tanh', linestyle='-.')
plt.plot(x.numpy(), leaky_relu(x).numpy(), label='Leaky ReLU', alpha=0.6)
plt.title("Common Activation Functions")
plt.grid(True, alpha=0.3)
plt.legend()
plt.ylim([-1.5, 1.5])
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.show()