为什么CNN中可以用卷积核提取相似度？

卷积神经网络中相似度的提取原理

原创已于 2022-06-26 19:16:43 修改 · 置顶 · 2.0k 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#cnn #人工智能 #神经网络

于 2021-10-21 10:13:49 首次发布

人工智能同时被 3 个专栏收录

155 篇文章

订阅专栏

数学

154 篇文章

订阅专栏

算法

101 篇文章

订阅专栏

本文介绍了卷积神经网络（CNN）如何通过卷积核提取图像与特征之间的相似度。利用线性空间理论和内积表示向量的相似性，卷积过程可以视为计算图像区域与卷积核的相似度。通过实例分析数字2和1的卷积结果，展示了卷积核在提取特定模式时的有效性。

老子说过，有道无术，可求也，有术无道，止于术，学道先于学术，懂得原理才算真的懂。

卷积神经网络的特征映射的值以图像和过滤器(卷积核)的相似度作为输入信息，卷积的过程表示如下：

假设由3x3像素构成的两幅图A,F，从矩阵向量相似的角度看，他们的相似度可以像下面这样求出:

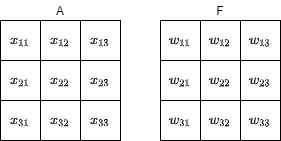
$\\\mathbf{S=w_{11}x_{11}+w_{12}x_{12}+w_{13}x_{13}+w_{21}x_{21}+w_{22}x_{22}+w_{23}x_{23}+w_{31}x_{31}+w_{32}x_{32}+w_{33}x_{33}}$

这个定理可以利用向量的性质来说明，根据线性空间理论，当两个向量 $\vec{a},\ \vec{b}$ 相似时，他们的内积 $a\cdot b$ 较大，我们可以认为内积 $a\cdot b$ 大小表示两个向量的相似性,cos的结果表示余弦相似度。

$\vec{a}\cdot \vec{b} = \left | a \right |\left | b \right |cos(\theta)$

图形化表示如下图，可以看到，当向量i和向量u方向大致相同时(夹角为锐角)，红色的投影长度比较大，而当两向量垂直时，投影为零，并且当向量夹角为钝角的时候，投影为负的向量，代表差异最大。

所以，为了利用这个性质，可以将两幅图像看成是向量：

$\\ A=[x_{11}, x_{12}, x_{13}, x_{21}, x_{22}, x_{23}, x_{31}, x_{32},x_{33}]\\ F=[w_{11}, w_{12}, w_{13}, w_{21},w_{22}, w_{23}, w_{31}, w_{32},w_{33}]$

这样一来，通过内积，卷积便和相似性联系起来，也就是说，我们可以把CNN中卷积的计算过程理解为提取图像区域和卷积核所表示的特征的相似度。

我们以数字2的识别为例，通过用一个3*3的卷积核来提取数字二的斜45度角特征。

可以看到，这个卷积核正确的提取了斜边的特征，和卷积核方向相同的部分，对应的卷积为3，其余所有有比零大的卷积结果，对应的单元中都有对应的斜边模式。从实践上这说明了通过设计合理的卷积核来提取图像特征的方法是合理的.

如果用此卷积核对数字1提取特征，会是什么样的结果呢？

通过对比两次的卷积结果我们可以看到，卷积结果清晰的反映了2比1更加相似于卷积核提供的模式，也就是说，卷积结果客观反映了针对某个模式的相似度，所以，神经网络里面使用卷积核是有它自己的道理的,过程用下图来表示：

总结:

如上面的几何分析，卷积结果可以认为是卷积核和卷积区域组成的向量的内积，而内积表示两个向量的相似度。

为什么CNN中可以用卷积核提取相似度？

总结:

结束！