神经网络的结构和原理入门

原创已于 2023-01-27 08:37:34 修改 · 置顶 · 1.6k 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#神经网络 #深度学习 #人工智能

于 2020-10-28 19:43:47 首次发布

嵌入式系统同时被 3 个专栏收录

354 篇文章

订阅专栏

人工智能

155 篇文章

订阅专栏

23 篇文章

订阅专栏

这篇博客介绍了神经网络的结构，将其与大脑的工作机制相比较，解释了神经网络中神经元如何通过权重线连接形成类似生物神经突触的功能。内容涵盖了全连接网络的概念，激活函数的作用，特别是sigmoid函数，以及神经网络的参数计算和训练过程。同时提到了一些神经网络的变种，如卷积神经网络和长短期记忆网络。

从仿生学的角度看，神经网络结构和大脑非常相似，大脑中的神经元有几百亿到几千亿个，我们的大脑在思考和记忆的时候，神经元就会互相传递信息，传递信息的神经元，与旁边的神经元相互连接的部分，叫做“神经突触”，大脑老化后，神经突触就没有连接功能了。

无论是短期记忆还是长期记忆，都是在神经突触连接神经元的过程中产生的，但是短期记忆神经突触的活动只是暂时增强，所以为了形成长期记忆，就要永久性增强神经突触的活动。

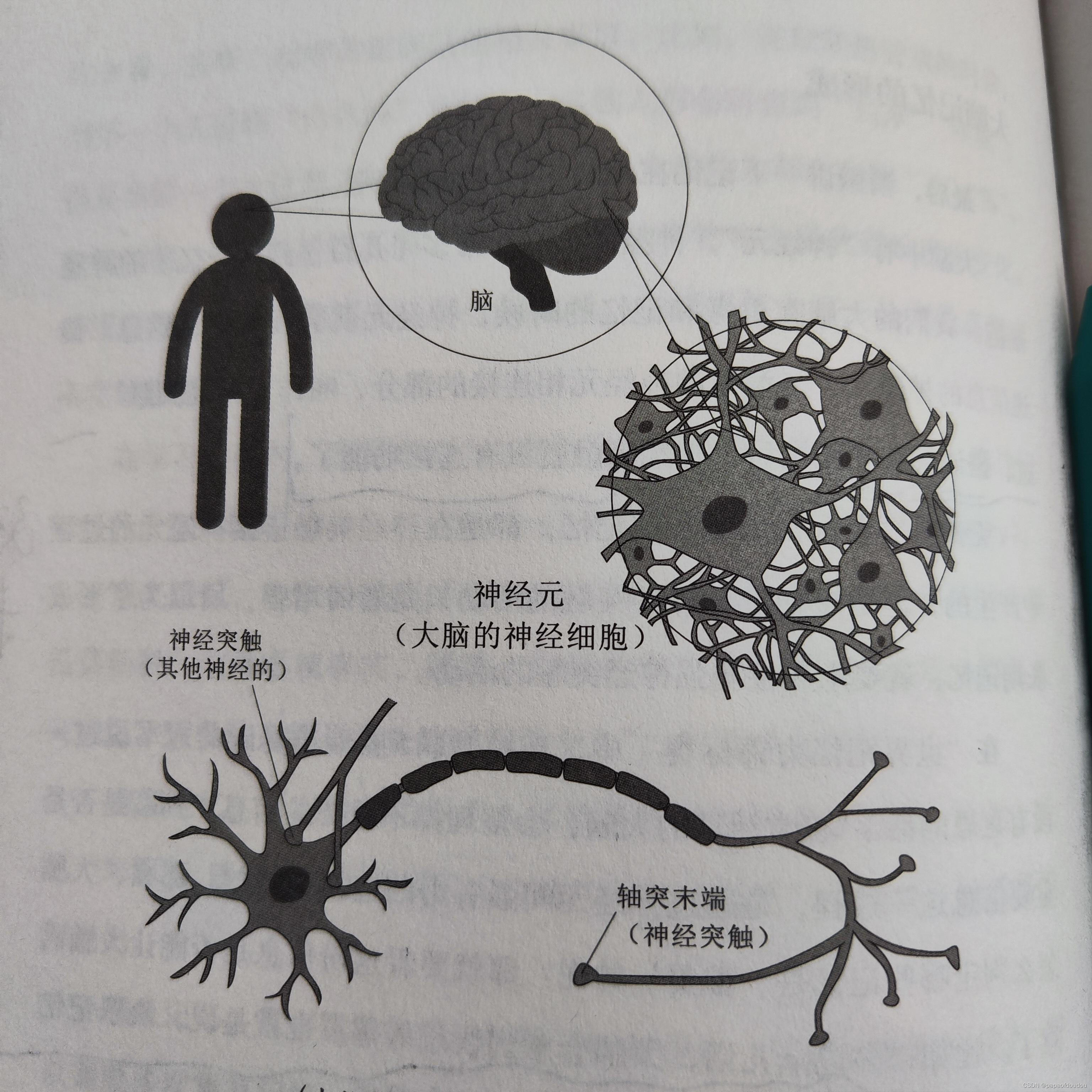
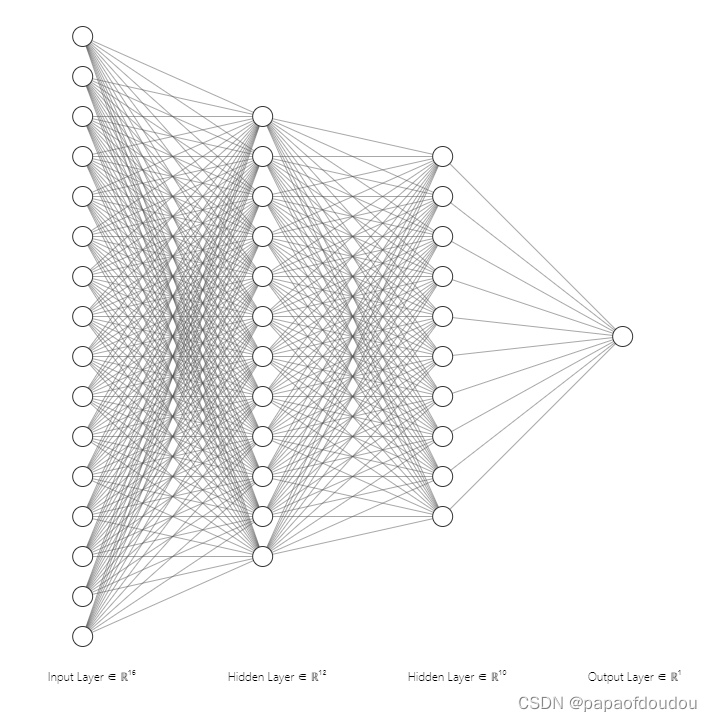
神经网络也是将各个独立的数据节点通过权重线连接在一起，充当数据节点之间突触的功能，在全连接网络中，每一个下级节点和上级的所有节点均有连接，以下图为例，一张图片上的所有像素点会被展开成一个1维向量输入网络，28 x 28的输入数据被展开成为784 x 1 的数据作为输入，其结构，简单示意图如下:　

神经网络的关键是中间的连线，而不是节点，工作时，上一层的激活值将决定下一层的激活值,所以，神经网络的核心在于，一层激活值是通过怎样的运算，算出下一层激活值的，某种程度上是模仿的生物大脑的工作机制。某些神经元的激发，会触发另一些神经元的激发。当被训练好之后，就可以识别固定的模式了。

简单来说，第一层的输入图形会导致第二层的某种图形模式，然后继续触发第三层，第四层。。。，直到最后一层。有点类似于链式反应，不过链式反应无法控制，速率越来越快，但神经网络最终都会收敛到一个或者几个有意义的结果输出。

神经网络比较数学化的描述：

单个神经元的原理如下：　　　　　

数学原理如下：

f一般取sigmoid函数，下面会有介绍，举个例子：

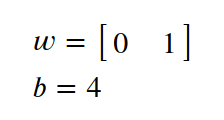
激励:

计算得到的输出是：

Size 28*28的图片含有像素点784各，构成输入向量

假设第一层的第i个节点对第二层的j的节点的权重为:

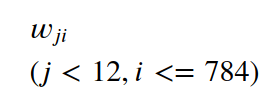
则

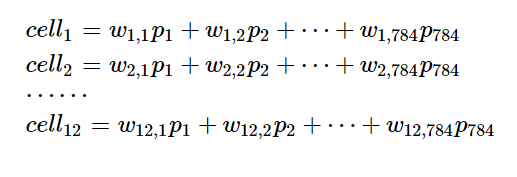
这样计算出来的神经元节点的值可以是任意大小，需要做归一化处理，常用的归一化函数是sigmoid函数，它可以将任意的数值映射为区间 [0,1]上的值，实现归一化处理，类似于将整个实轴压缩到(0,1)区间。

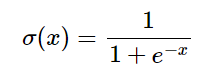
其函数图象为:

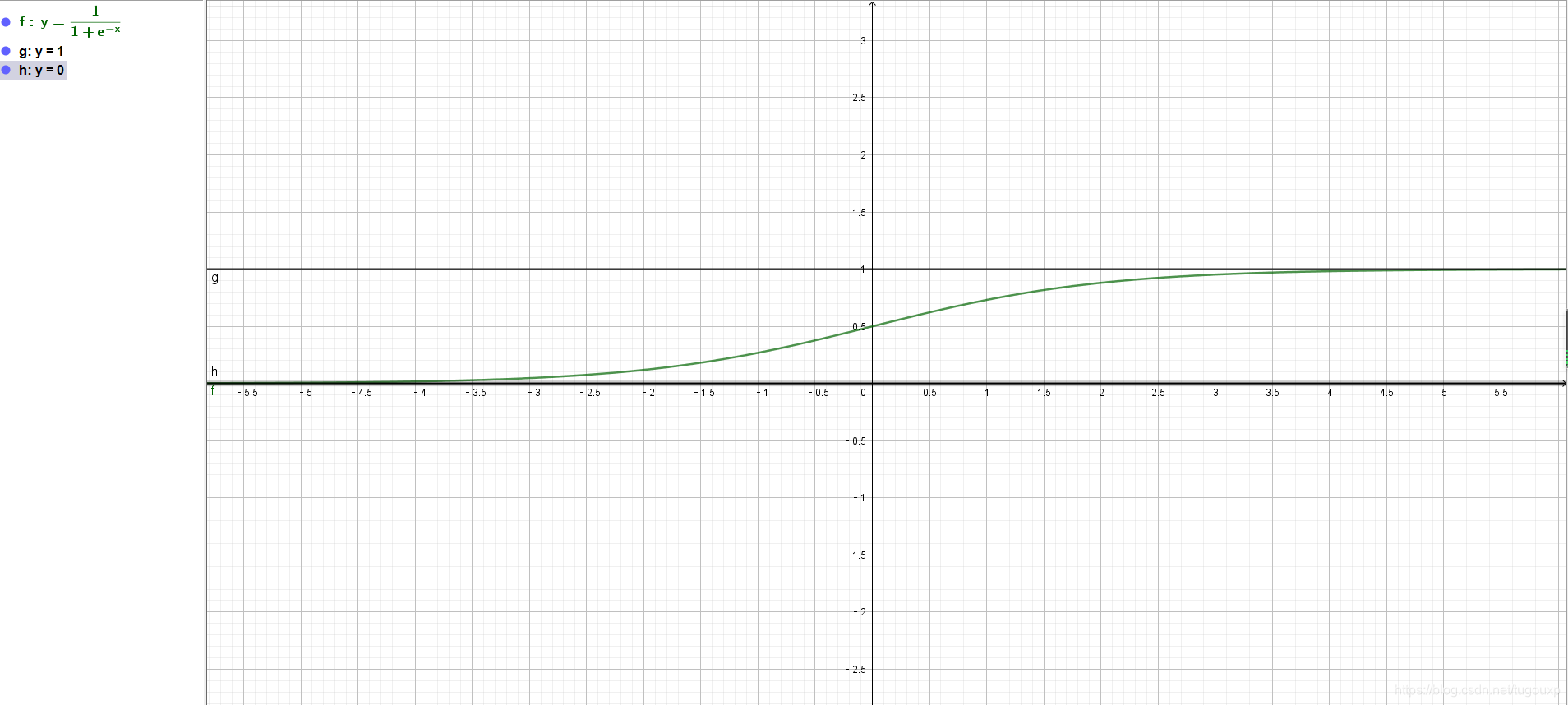
在各自的定义域上，sigmoid既是单射，又是满射。细节上：　　　　　　　　

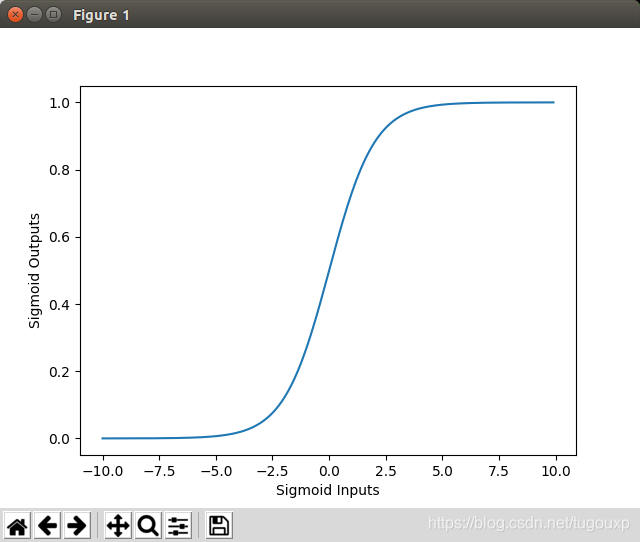
常用的激活函数包括sigmoid,sotplus,tanH等等，他们的图像和定义分别是：

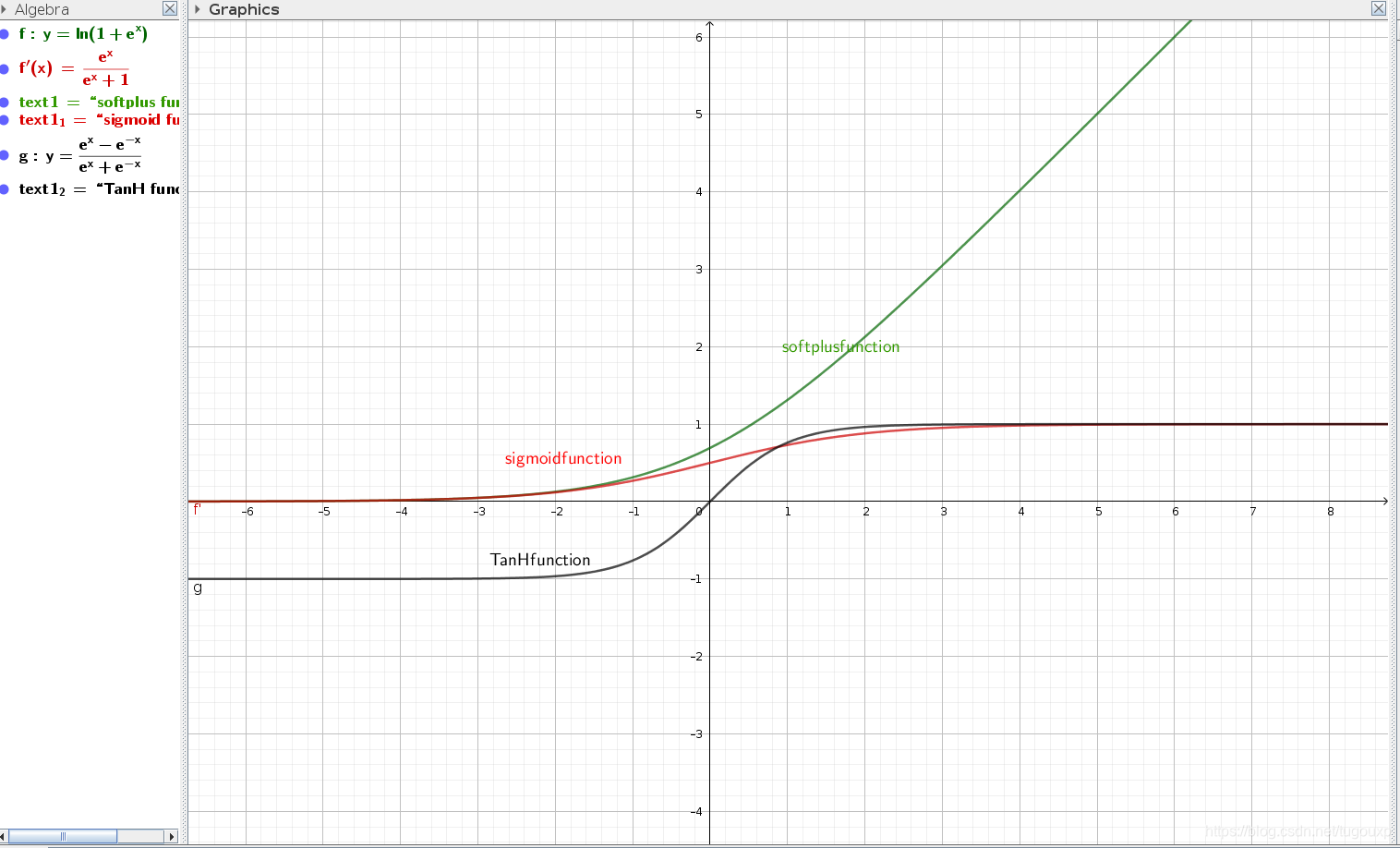
需要注意的是，sigmoid恰好是softplus function的一阶导函数,即:

${(ln(1+e^x))}'=\frac{e^x}{1+e^x}$

简而言之，它能把非常大的负值转换为接近于0，又能把非常大的正值转换为接近于1，在0值附近则是平稳增长。

所以，实际上神经元激活值应该要在对上面的计算结果取一个sigmoid变换，通常还要再加上一个偏置换阈值。

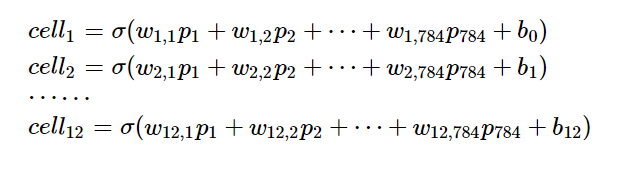
转换为一般形式是：

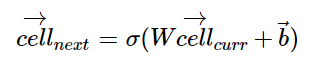
这种形式简单很多，而且更有代表性。

传递矩阵为

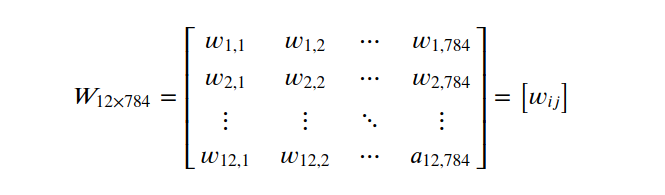
W矩阵第一维代表后层的节点，第二维标识前层的节点.

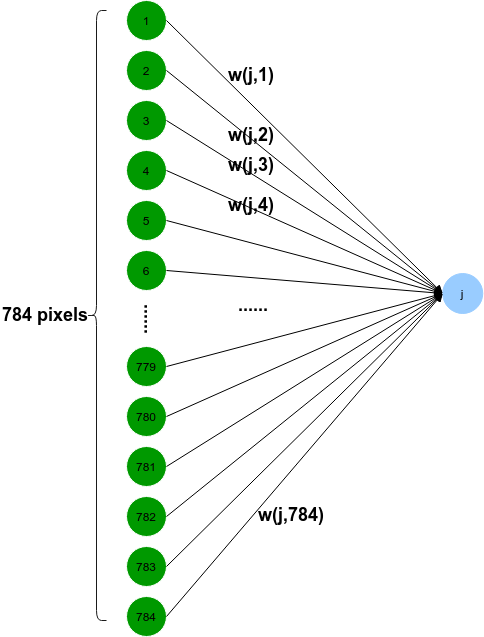
上面是一个全连接（fully connected layers，FC）的模型，全连接意味着输出向量中任何一个具体的输出神经元都由全部的输入神经元来决定，具体运算可表示为输入向量和一组突触权重向量之间的内积，再加上偏置，然后通过激活函数输出，可以形式化地表示为:

$\boldsymbol{y[j]=G(b[j]+\sum_{i=0}^{784-1}W[j][i]\times x[i])}$

i为前层神经元数，j为后层神经元数，可以看到全连接的核心计算是向量内积，即输入与权重做向量内积运算，然后与非线性激活函数相加，每个变量都要经过激活函数处理。

可以看到，全连接单个输出神经元的计算为向量内积，而多个输出神经元聚合在一起时的计算就变成了矩阵向量乘，因此，深度学习处理器的实现中，计算指令可以包括矩阵指令，向量指令，当然，还有标量指令三类。

全连接层在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。在实际使用中，全连接层可由卷积操作实现.

从前级节点的角度看，下级神经元节点相当于上级节点带权列向量的线性组合，也就是，落在上级节点的线性子空间里面。　

注意，这里是权重的子空间，而不是对应层神经元的子空间，从下面公式可以看出来。　　　

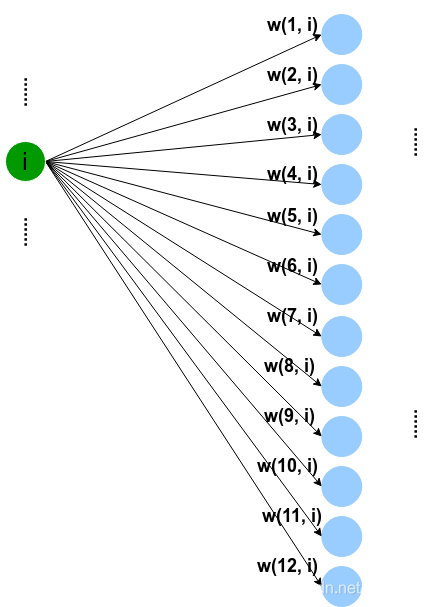
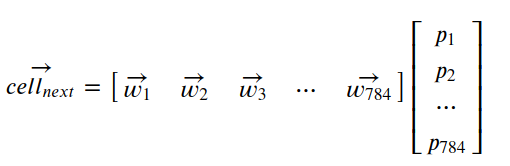
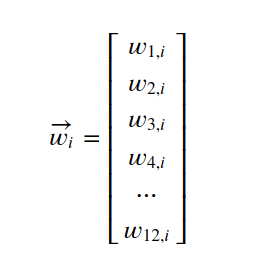
可以简单的做个类比，左边的第一层相当于太阳，右边的网络层相当于行星。每个太阳对所有行星的辐射能力不同，他们组成了矩阵的列向量。有多少个太阳，就有多少个列向量。

所以第二层网络所获取的辐射能量相当于每个太阳辐射列向量和太阳本身能量乘积的和。也可以理解为第二层网络单个神经元获取的能量等于每个太阳针对这个星球的辐射加权和.

还可以理解成,下级神经元获得的能量等于上级子节点构成的向量在针对当前下级神经元的权重向量上的投影.

神经网络既可以看成参数的容器，也可以从整体上看成一个函数，多输入多输出的函数，或者是一种集合的映射。

只是从参数角度看，参数实在太多，而且还有大量的矩阵类，归一化，累乘累加运算，导致需要极大的算力，普通的CPU根本难以承受。

单纯考虑不同层之间的传递关系，单层网络的传递函数是：

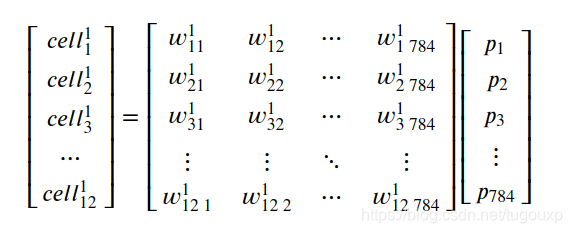
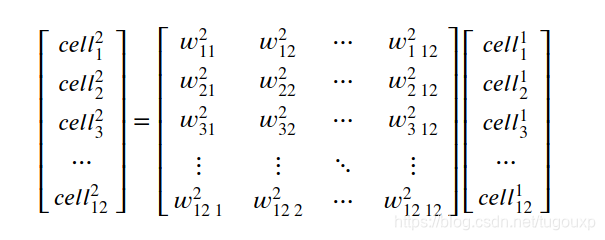
所以：

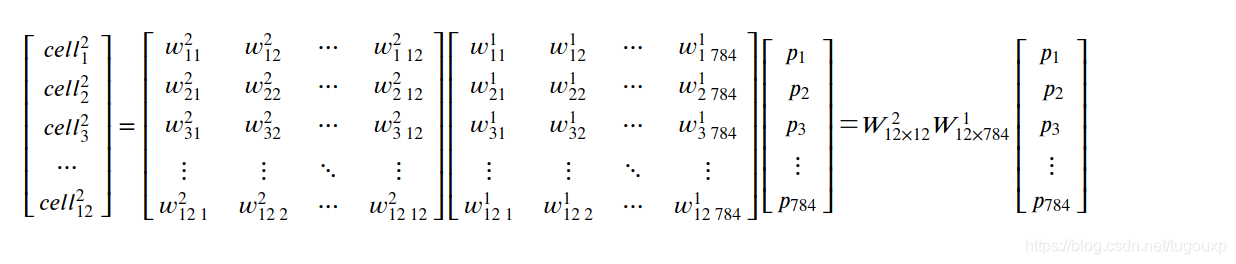
所以，第三层和输入层的传递关系是：

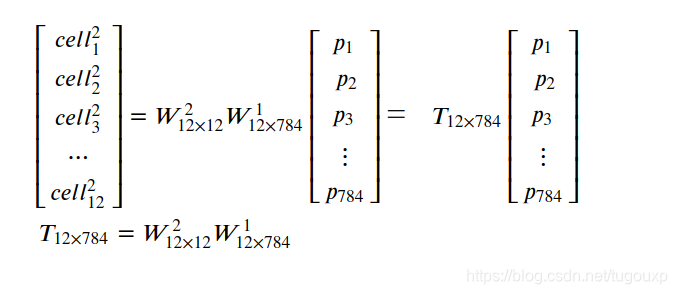
所以,跨越层之间的传输矩阵，是不同层权重矩阵连续相乘。

看成函数的话，每一层的输入时上一层神经元的输出（除了第一层是数据输入外），而每一层的输出又成为了下一层的输入。整体上看，输入经过网络的处理后，变成了输出，例如，上面的网络可以看成如下784输入10输出的函数：

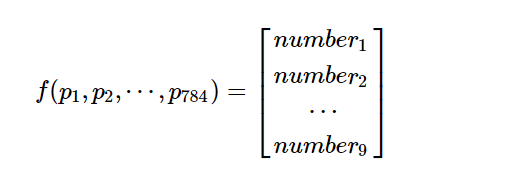
只是这个函数过于复杂，以上面的网络为例，它使用了

784*12 + 12*12 + 12*10=9,672

权重，以及

12 + 12 + 10 = 34

个偏置。

总共9,672 + 34=9706个参数

来识别图形。

不过话说回来，识别图形本身就是很复杂的运算，这货不复杂还真不行。

关于神经网络是如何获取合适的权重和偏置的，就涉及到训练了。

神经网络的变种非常多，典型的：

卷积神经网络(convolutional neural network)适合于做图像识别

长短期记忆网络(long-short term memory network) lstm适合于做语音识别.

神经网络算子是什么:

算子一次处理一层，还是一个神经元？答案是一次处理一层，有些框架会优化，比如卷积，池化，激活三个层一起跑。这也解释了libonnx项目跑mnist的时候，调试发现只跑了11个算子。但网络显然不止这么多节点。同一层的处理是相似的，同一层同样的功能。可以这样理解的。

图10 批量操作

其它：

神经网络结构观察工具，如下网址可以自定义一个神经网络并查看结构：

NN SVG

神经网络的结构和原理入门

结束！