什么是计算图

什么是图：

按照数据结构的定义，图由顶点集V(G)和边集E(G)组成，记为G=(V,E)。其中E(G)是边的有限集合，边是顶点的无序对（无向图）或有序对（有向图）。

对有向图来说，E(G)是有向边（也称弧(Arc)）的有限集合，弧是顶点的有序对，记为<v,w>，v、w是顶点，v为弧尾（箭头根部），w为弧头（箭头处）。

对无向图来说，E(G)是边的有限集合，边是顶点的无序对，记为(v, w)或者(w, v)，并且(v, w)=(w,v)。

例子：

  微信是有向图，因为你钓妹子不成功，妹子把你删了后仍然出现在你的好友列表里，只是再也接收不到你发的信息而已。

  QQ则是无向图，妹子把你删了之后，连带着会影响你的好友列表，从你的好友列表里面消失，从此你们各过各的，互不影响。

什么式计算图：

　计算图就是将计算过程图形化表示出来。是一种描述方程的“语言”，既然是图，则有节点（变量），边（操作（简单函数））。下面是个例子：

　　　　　　　

怎么用呢？

结合链式法则可以对给定计算图表示微分

　

经过逐级放大，x的变化传递到y，根据链式求导法则:

                               

另一个例子：

                 

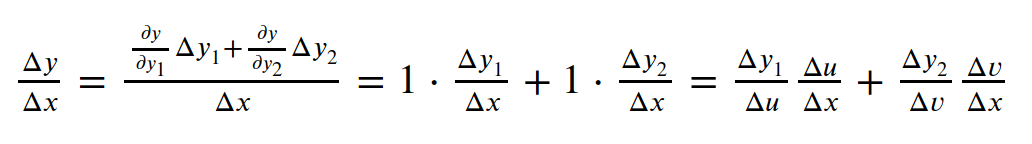
复杂一些的例子：

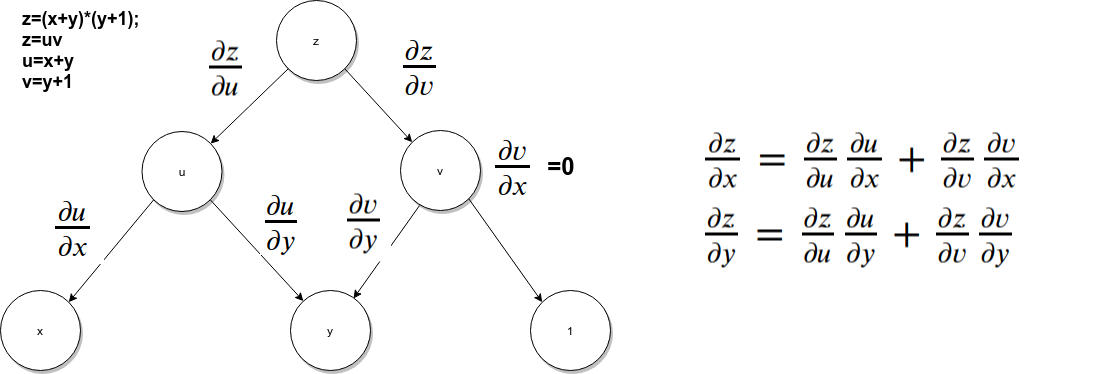
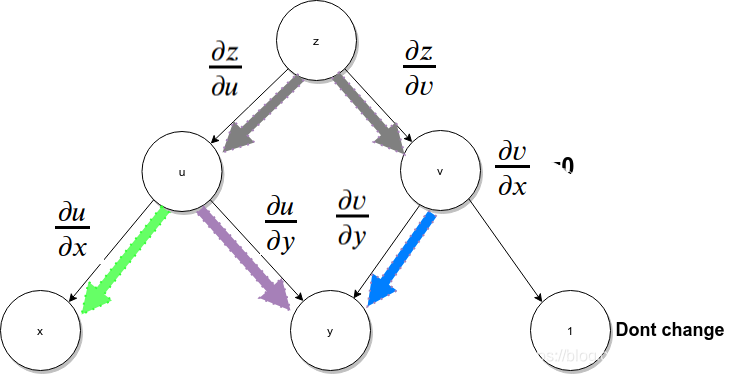
如果求上图中z对x,y的偏导(偏微分),等于x, y到顶点z所有路径的微分的和。步骤如下：

1.计算每个边对应的微分,比如：

  

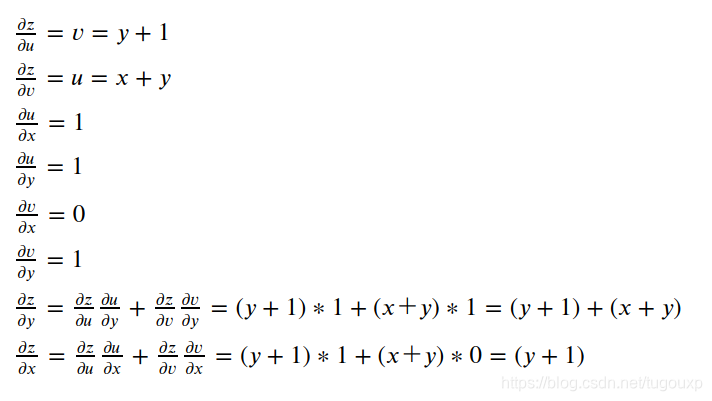
2.对于每条从z到y，x的路径，所有边的微分相乘求得该路径上的微分。

3.将该变量到z所有路径上的边乘积得到的微分相加.

从计算图数据流向的角度，相当于每个图中每个终端节点（代表自变量)的微小变化反馈给顶层节点的过程，所谓蝴蝶效应，这里可以类比为变元x,y对z引发的蝴蝶效应，所以，从这种角度来看，可以按照下图中颜色箭头标识的路径来理解。

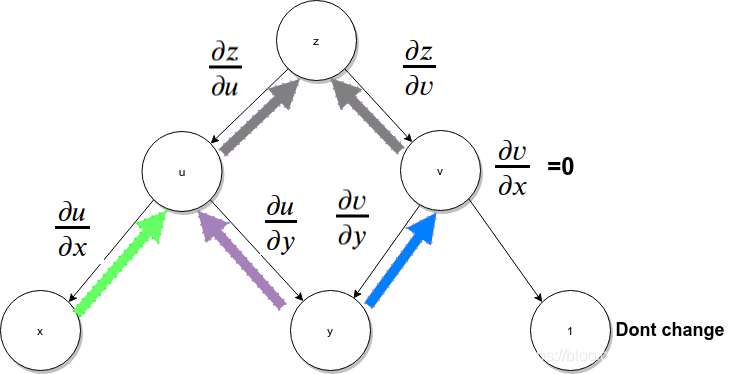
当需要求多个变量的偏微分时，反向的模式（从根开始）更有效率
计算方法一样【本质是一样的，可以理解成，链式法则相乘的部分顺序颠倒】

下面的流程比较好理解，可以看成是正常的多元函数微分求导的过程。

就像是剥洋葱，简单的说，上上图标识的从里往外面剥（四维空间可能能办到 :) )，而上图则是正常的剥法，从外向里面剥.

计算图中，可能会出现同一个节点出现在图的不同位置的情况，比如，如下函数的计算图:

                             

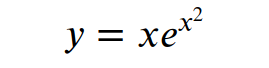
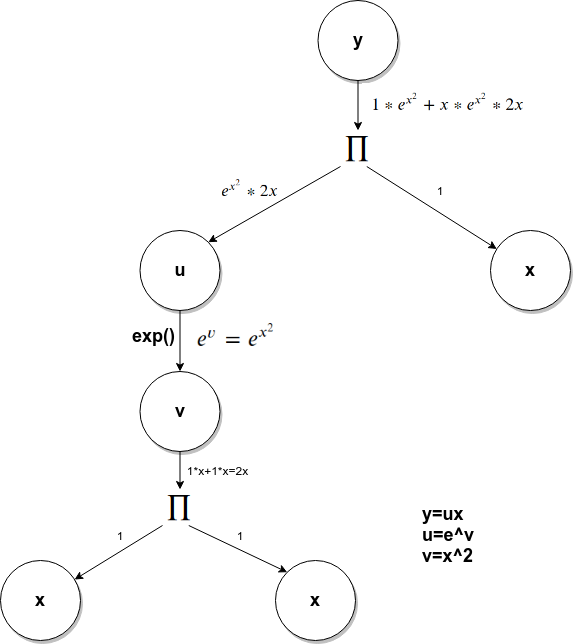
x节点出现在了图结构的不同位置，对于这种的处理方式仍然是把他们当做不同的节点，不同的变量求微分处理。

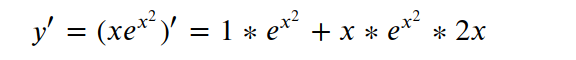
BP的理解：

BP是Back Propagation的简称.

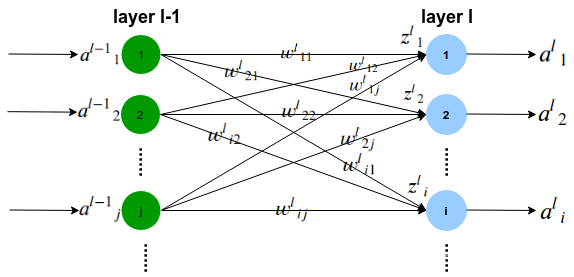
信号的传递关系如下公式描述:

其中是非线性函数，也叫激活函数。

Loss:损失函数

     :激活函数
  : l -1层的第j个节点 与 l层的第i个节点 的连接权重
    : 第l层的输入
:第l-1层的输出

：第l层的输出

前向传播递推公式:

输入关系：

第一层的输入是样本数据，后续中间层的输入是前层的输出向量。

Loss函数可以看成是对各个权重和偏置的多元函数：

则: