如何判断一个点是否在一个线段上

        假设有三维线段AB，如果三维点P在线段AB上，那么向量PA和PB的点乘必定小于或者等于零，同时叉乘必定为零向量。下面为这个结论做个简单的解释。

        如果向量PA和PB的点乘的结果大于零，那么点P必定位于以线段AB为直径的球体的外部；如果向量PA和PB的点乘的结果等于零，那么P点位于以线段AB为直径的球体表面上（包括线段AB的两个端点），此时PA与PB垂直；如果向量PA和PB的点乘的结果小于零，那么那么点P必定位于以线段AB为直径的球体的内部。如下图所示（这里使用平面的圆形，而不是三维的球体，不是什么严谨的论述，实用就好，呵呵）：

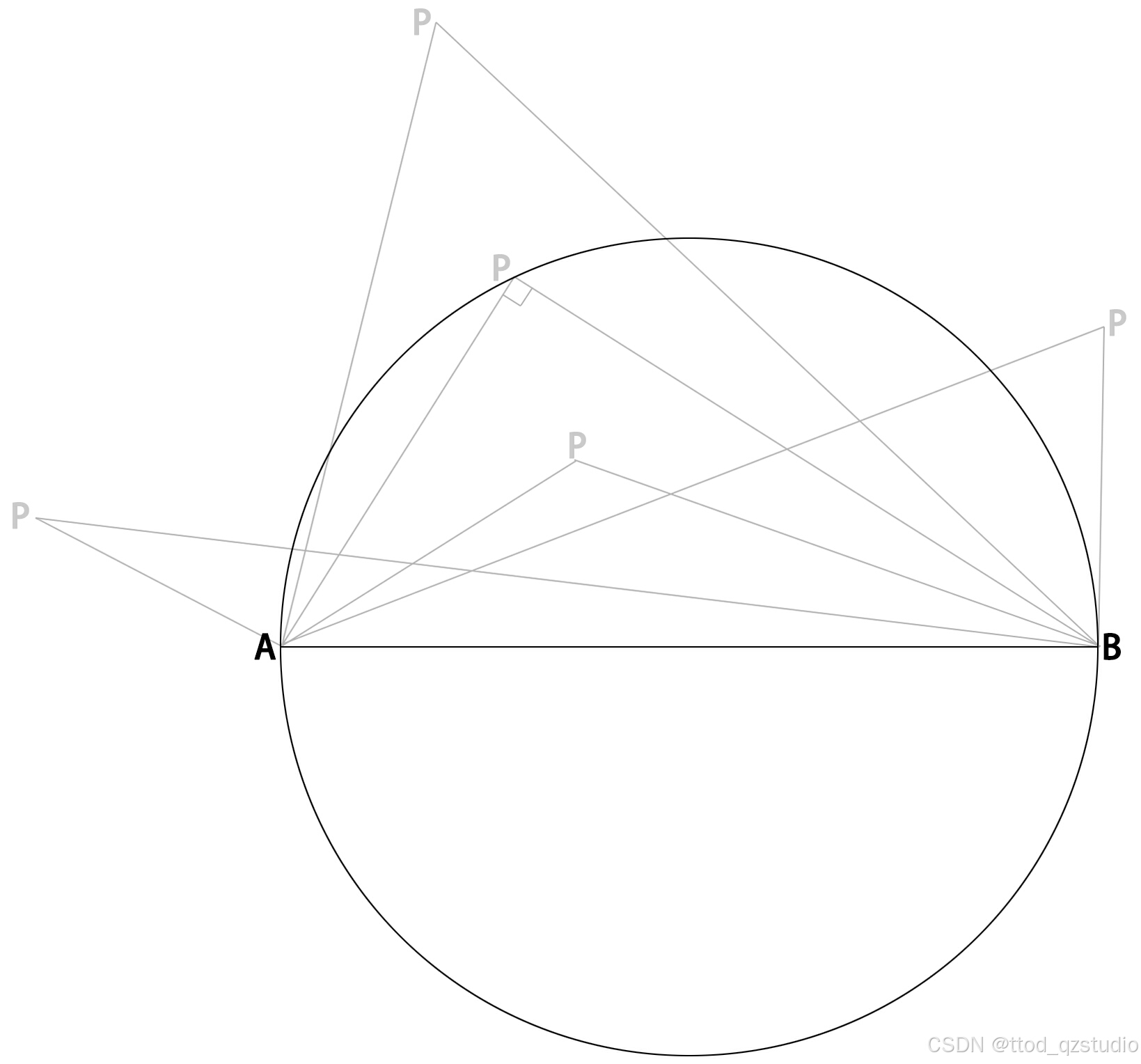
        如果PA和PB的叉乘为零向量，那说明PA和PB平行，即方向完全相同或者完全相反，而由于向量PA和PB的点乘的结果小于等于零，那么那么点P必定位于以线段AB为直径的球体的内部或者圆上（包括线段AB的端点），这就排除了PA和PB方向完全相同的情况，所以P点必定位于线段AB上。如果需要排除P点与AB端点重叠的情况，只需要判断向量PA和PB的点乘的结果小于零，而把等于零的情况排除就可以了。

        其判断代码参考如下：

bool PointOnSegment(Vector3 point, Vector3 pSegA, Vector3 pSegB)
{
	Vector3 vecA = point - pSegA;
	Vector3 vecB = point - pSegB;
	if (Vector3.Dot(vecA, vecB) > 0) return false;
	if(Mathf.Approximately(Vector3.Cross(vecA, vecB).sqrMagnitude,0)) return true;
	return false;
}