非保守力场中求力的做功 （思路）

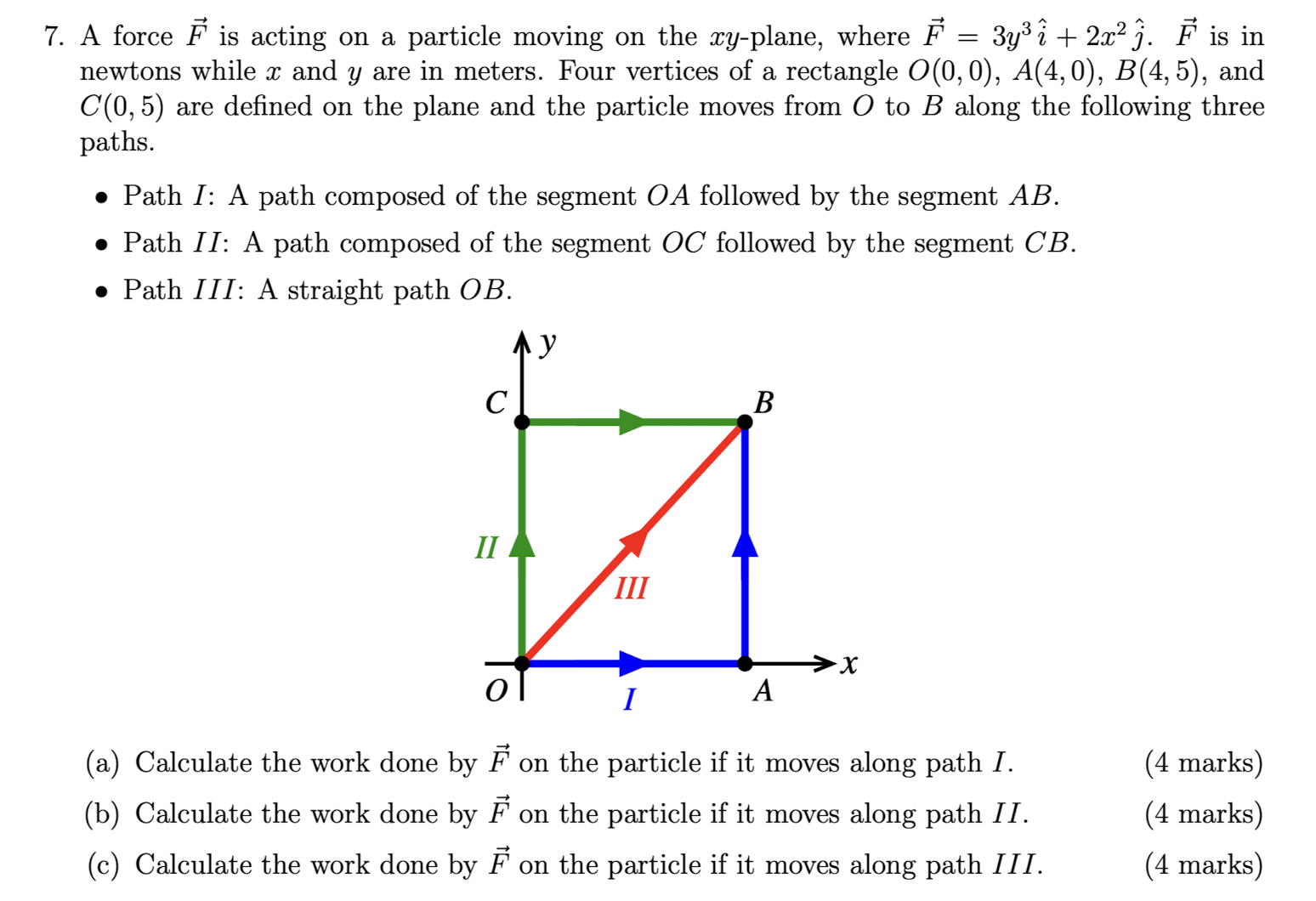
如题，根据题目信息，可得F是非保守力，受力物体的路径影响做功大小（保守力，比如地球的引力或者在匀强磁场力的磁力，物体运动轨迹不影响做功大小）

和ab问不同，c问中在x变化时y也在变化，不好同时处理x和y的积分。那么可以将路径参数化，用参数统一处理x和y的变化。对于这种题目的思路：

1. 用参数方程写出路径

$$\vec{r}(t) = (4t, 5t), \quad t \in [0,1]$$

将物体的位置用参数t表达，可以想象成时间，这样物理意义比较好理解，物体用1s从 (0,0) 走到了 (4,5)

2. 用参数表达力

$$\vec{F}(\vec{r}(t)) = \bigl( 3(5t)^3, \, 2(4t)^2 \bigr) = (375t^3, \, 32t^2)$$

将用t表达过的x和y代入力的向量，得到一个只用t表达的力

3. 积分转化

注意到W = Pt = Fv t = 积分符号Fv dt

求v：对r(t)求导

注意Fv是上一步求的F(r(t))和v，也就是r'(t)，的点乘

然后算积分即可

$$W = \int_0^1 (1500t^3 + 160t^2)\, dt$$