改进Henon映射在图像加密中的应用

改进的Henon映射在图像加密中的性能评估

1 引言

安全性在多媒体通信中起着重要作用。加密是满足数据存储和传输安全需求的方法之一。传统的加密方法如数据加密标准（DES）、国际数据加密算法（IDEA）和高级加密标准（AES）由于速度慢、复杂性高、数据量大以及像素之间存在高度冗余，不适用于图像加密[1]。为了克服这一难题，已提出许多新的加密技术以确保安全通信。混沌基于算法因其具有对初始条件/系统参数的高度敏感性、不可预测性、高安全性和简单性等动态特性，成为所有加密技术中实现安全多媒体加密的一种新颖且高效的方法[2]。

许多研究人员已经识别出混沌系统在被称为映射的迭代函数中的动态和无序行为。这些映射可以通过离散时间或连续时间域来表征。由于其独特的特性、快速加密速度和简单结构，其中一些研究在安全系统的开发中利用了各种一维和二维混沌映射。通过对现有混沌映射进行修改，从而识别并改进混沌区域，这是动力系统理论中一个令人兴奋的研究领域。已提出多种基于一维混沌映射（如Logistic映射[3],正弦和帐篷映射[4]）的图像加密算法。在[5],中已指出，由于密钥空间小和安全性弱，一维混沌映射不能用于图像加密。显然，通过使用两个一维Logistic映射可以消除这些缺点[6]。

此外，通过增加维度可以增强安全性，而维度的增加会进一步提高非线性。高维混沌系统由于其时间序列难以预测以及具有更多的正的李雅普诺夫指数，因此被广泛应用于多媒体加密中。李雅普诺夫指数用于表征和量化持续的混沌行为。此外，在高维混沌系统中，加密的基本操作如置乱与扩散可以在多个方向上进行，有助于快速消除像素之间的相关性[7]。法国数学家兼天文学家米歇尔·埃农在1976[8]提出了一种称为Henon映射的二维映射。该映射具有二次非线性，表现出混沌特性，结构简单易于实现，并且便于进行数值探索。由于图像是像素的二维数组，因此二维Henon映射被用于基于混沌的分块图像加密[9]。

基于此背景，对Henon映射进行了改进，以扩大混沌区域，从而进一步提升安全性。本文通过对改进的Henon映射进行详细的分析研究，并将其应用于图像加密中。

本文结构安排如下。相关工作的概述在第2节中给出。修改Henon映射所需的数学基础、映射的动态行为以及仿真结果在第3节中进行了阐述。混沌映射在图像加密中的一些特殊性质和应用在第4节中提供。安全性分析的结果在第5节中给出。结论部分在第6节中。

2 相关工作

本节介绍了图像加密相关工作的简要概述。通常，基于混沌的图像加密方案采用置乱与扩散两种基本操作。通过置乱操作可以降低相邻像素之间的强相关性。在扩散阶段，像素值被改变，从而在整个图像上获得统一的效果。通过多次重复这些操作，可以获得满意的安全性水平。

在[2],中，作者提出了一种基于分段线性混沌映射的新图像加密方案。明文图像被转换为两个二进制

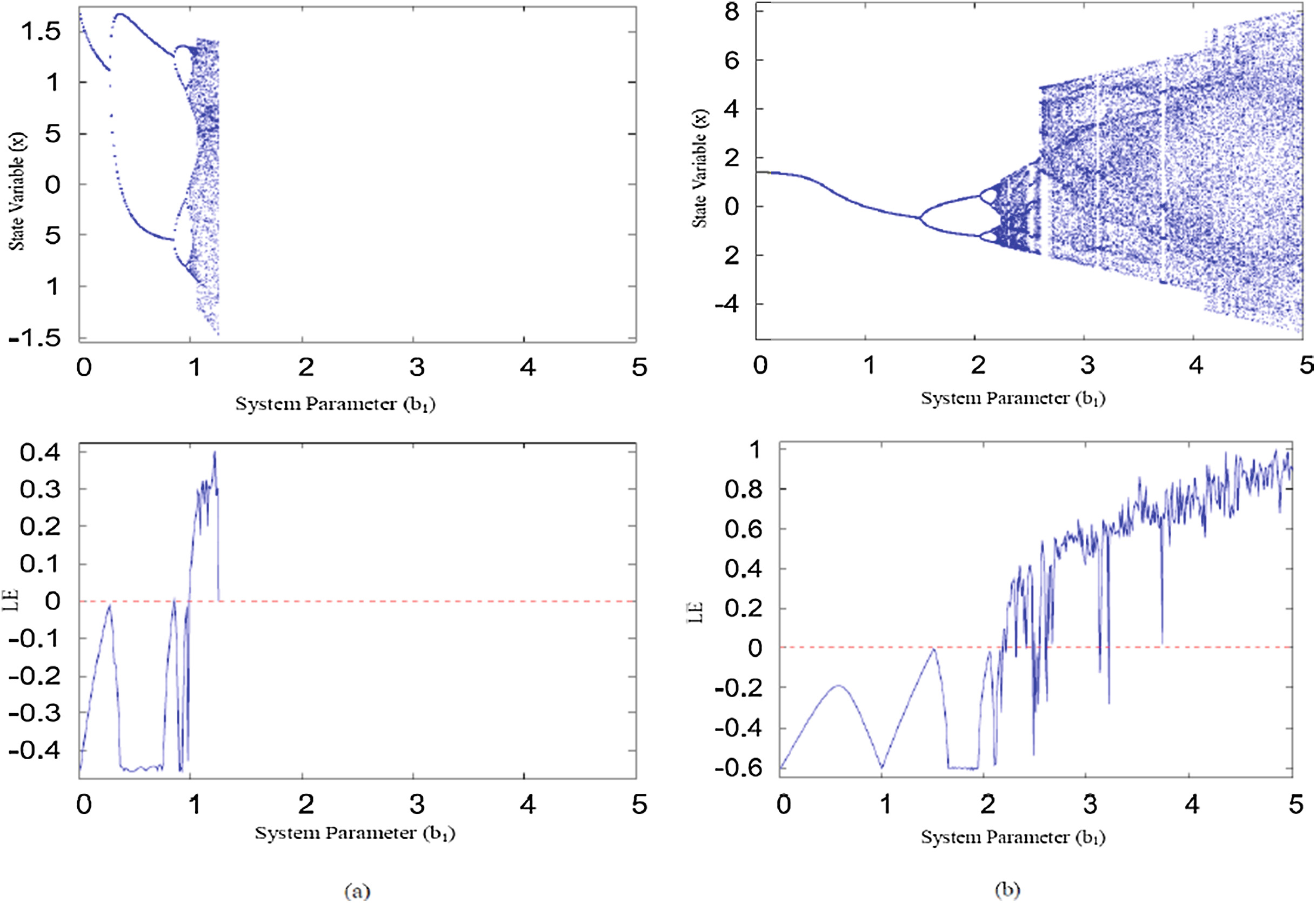Henon映射在系统参数(b2= 0.3)下的分岔图和李雅普诺夫指数。(b) 改进的 Henon映射在系统参数(b2= 0.3)下的分岔图和李雅普诺夫指数。)

通过密码系统生成相同大小的序列。扩散阶段通过两个序列之间的相互扩散实现，而在混淆阶段，由混沌映射控制对这两个序列的二进制元素进行交换。文献[10]提出的一种新型密码系统利用了两个扰动分段线性混沌映射和异或操作。混沌流通过将两个扰动分段线性混沌映射的结果进行异或操作组合而成。将生成的混沌流与明文进行异或操作以获得密文。文献[11]提出了一种基于Logistic映射和异或操作的混沌图像加密算法。该方法使用异或操作来混淆像素值，并通过对像素置乱得到加密图像。文献[12]提出了一种基于Chua混沌系统的图像密码系统。该密码系统采用索引和置乱机制进行加密。在[13],中，提出了一种基于切比雪夫生成器的图像加密方案，该方案使用两个伪随机序列进行置换，并在扩散阶段结合二维切比雪夫函数。文献[14]提出了一种基于广义Arnold映射、置换和扩散的图像加密方案。通过使用全圆函数降低相邻像素间的强相关性，并采用双重扩散函数实现扩散。

文献中提出的几种图像加密方案各有优缺点。本文研究了改进的Henon映射在图像加密中的性能。基于改进的Henon映射的密码系统能够抵抗多种攻击，并且与文献中其他算法相比，降低了像素之间的相关性。

3 数学基础

让我们考虑一个 K 维度的离散动力系统。其迭代映射 f：RK → RK 具有如下形式
xk+1= f(xk) (1)
其中 k= 0，1, 2… 表示离散时间，xk ∈ RK 表示状态。函数 f: R2 → R2 称为在 R2 中的映射。Henon映射是R2 中最简单的可逆映射，其表达式为
xk+1= 1 − b1x 2 k+ b2yk yk+1= xk
(2)
这里(xk, yk)表示系统的二维状态。系统参数 b1和 b2在一定取值范围内可产生混沌吸引子。为了获得混沌吸引子的精细结构，系统参数不应过大或过小。如果 b1太小或太大，则混沌吸引子不存在。如果 b2过于接近零，收缩区域将过大；另一方面，如果其值太大，则折叠不够强烈。通过将 b1和 b2分别设置为1.4和0.3，可以获得混沌吸引子的精细结构[8]。Henon过程允许修改两个参数 b1和 b2以获得其他混沌吸引子。有界解可以获得

通过选择适当的非线性项和系统参数，Henon映射在参数值 −1< b1< 2和|b2| < 1时具有有界解，并且在一定取值范围内可以获得混沌吸引子。这在安全通信中具有应用[9]。

改进的Henon映射由下式给出
H(xk, yk)=(xk+1 yk+1) =(1 − b1cos(xk)− b2yk −xk ) (3)
在原始Henon映射中，x2k项被非线性项 cos(xk)和 b2 = 0所替代。对于改进的 Henon映射，对于所有 b1和 |b2| < 1的值均可获得有界解。通过选择其中一个系统参数 b2= 0.3，可以获得较宽的混沌区间。

备注 ：
1. 映射 H(xk, yk) 是定义在 R2 上的可逆映射，除非 b2 = 0。
2. 改进的Henon映射的雅可比矩阵为 Df(xk, yk) =( b1sinxk −b2 −1 0)，其中 detDf(xk, yk) = −b2 对所有 xk, yk ∈ R2 成立，且对于固定的数b1 和 b2。特征值由下式给出
λ= b1sin(xk)± b1sin(xk)√1+ 4b2 b21sin 2(xk) 2 (4) 特征值是实数，如果 √1+ 4b2 b21sin 2(xk) ≥ 0
3. 由于该映射的雅可比矩阵的行列式为 −b2< 0，因此相空间的体积随着时间演化而缩小，所以该映射是耗散的[15]。

3.1 参数变化下的动力学行为

在本小节中，研究并比较了系统参数变化下原始Henon映射以及改进的 Henon映射的动态行为。为了在特定应用中使用混沌映射，有必要了解混沌区域，这就需要对动态行为进行分析。离散映射的动态行为会以多种方式突然从不动点和周期点转变为混沌行为。这可以通过分岔图和最大李雅普诺夫指数来验证，它们有助于找到混沌区域，从而确定不动点和周期点。原始Henon映射的分岔图和李雅普诺夫指数（LE）通过在区间 0 ≤ b1 ≤ 5内改变系统参数，并针对状态变量（x）在 b2= 0.3情况下绘制，如图1(a)所示。对于改进的 Henon映射，这些图在相同范围内绘制，如图1(b)所示。当 b1= 1.5时，不动点失效，出现周期二轨道。直到 b1= 2.0537，周期二轨道为吸引子，随后其周期发生倍增。当 b1= 2.0537且 b2= 0.3时，改进的Henon映射的吸引子变得更加复杂。当周期二轨道变得不稳定时，立即出现周期四轨道，然后

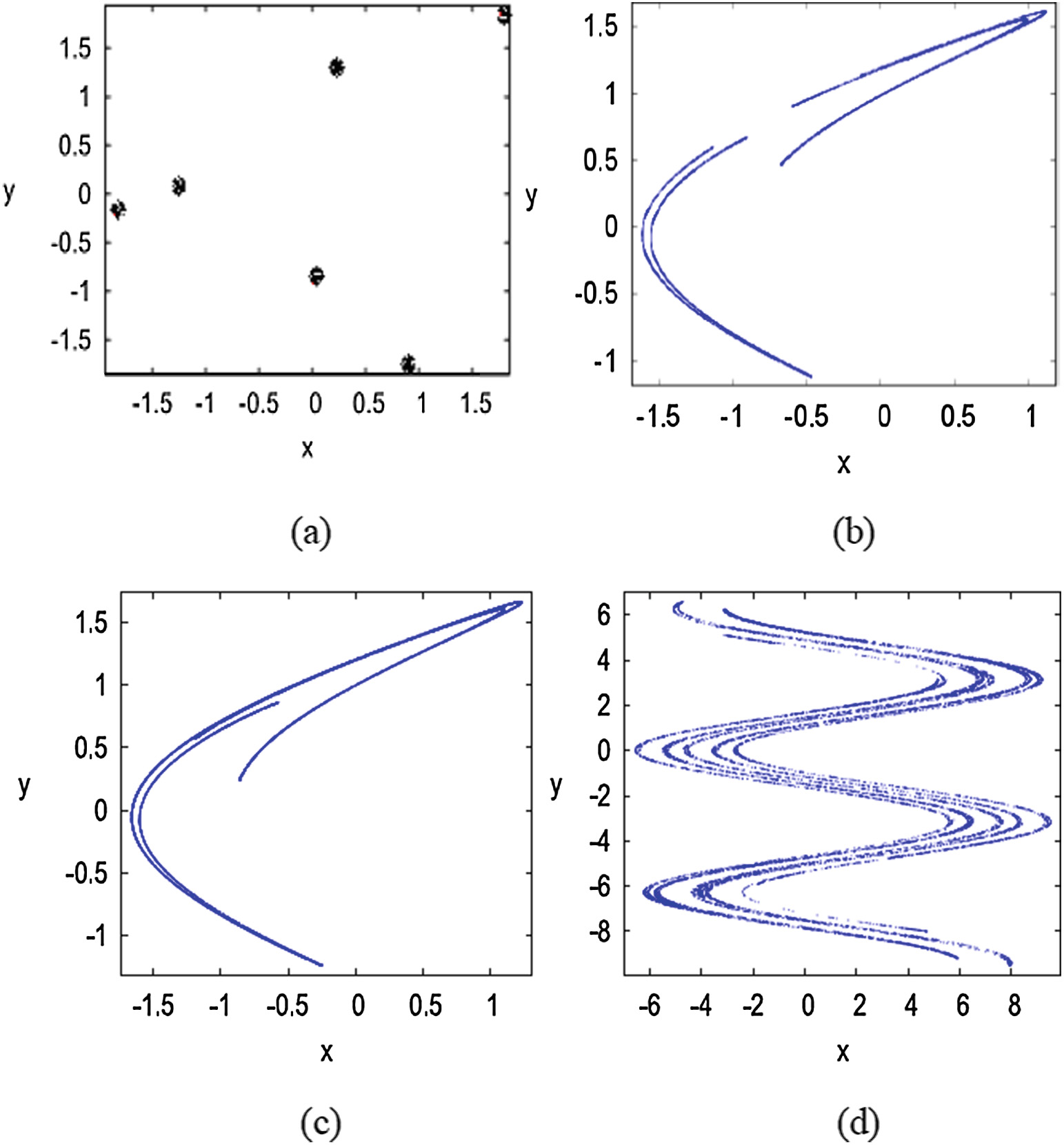b1= 2.53，六周期吸引子。(b) b1= 2.25，双片段吸引子。(c) b1= 2.3，单片段吸引子。(d)b1= 6，多重吸引子。)

八周期轨道等，在区间 2.0537 ≤ b1 ≤ 2.19内。该映射在区间 2.19 ≤ b1 ≤ 2.5内收敛到一个混沌吸引子。当 2.5 ≤ b1 ≤ 2.54时，该映射收敛到一个不动点。当 b1> 2.54时，该映射进入混沌状态。图 2(a) 展示了在 b1= 2.53处的六周期汇，在图1(b) 中表现为一个微弱可见的白色间隙。使用 b1= 2.25可获得双片段吸引子，如图2(b) 所示。在 b1= 2.3处，双片段吸引子合并形成单片段吸引子，如图2(c) 所示。为了展现多折叠吸引子，改进的Henon映射经历了倍周期分岔，如图2(d) 所示。尽管原始Henon映射通过倍周期分岔级联进入混沌区域，但它并不具备多折叠吸引子。从相图中可以明显看出，适当选择系统参数可导致多折叠混沌吸引子 [15]。改进的Henon映射的不动点区域和混沌区域总结于表1中。

3.2 混沌区间的比较

分岔图和同一范围内的Lyapunov指数用于比较Henon映射与改进的Henon映射的混沌区间，如图1(a)和(b)所示。从图中可以看出，Henon映射在 b1 ∈[1.05, 1.4]范围内是混沌的，而改进的Henon映射在区间 0 ≤ b1 ≤ 5内的 b1 ∈[2.2, 5]范围内是混沌的。在此区间内，Henon映射和改进的Henon映射的混沌范围比率分别为7%和56%。因此，由于混沌区间从7%增加到56%，改进的Henon映射在多媒体加密中具有更广泛的应用。

3.3 李雅普诺夫指数和维度

如果李雅普诺夫指数中有一个为正，并且负指数幅值应大于正指数幅值[15]，则称该映射是混沌的。此外，对于二维映射，LE1> 0> LE2和 LE1+LE2< 0。该映射的李雅普诺夫指数由 LE1= 0.589059和 LE2= −1.793032给出，分别对应于 b1= 3和 b2= 0.3。相应的李雅普诺夫维度由DL= 1.3285给出。

4 随机性测试与映射的密码学应用

在本节中，通过仿真结果展示了混沌映射的若干显著特性，例如对初始条件/系统参数的敏感依赖、随机行为、自相关以及互相关特性。

4.1 对初始条件的敏感性

系统参数变化下状态变量的混沌行为如图3(a)所示。该映射对微小变化的敏感性

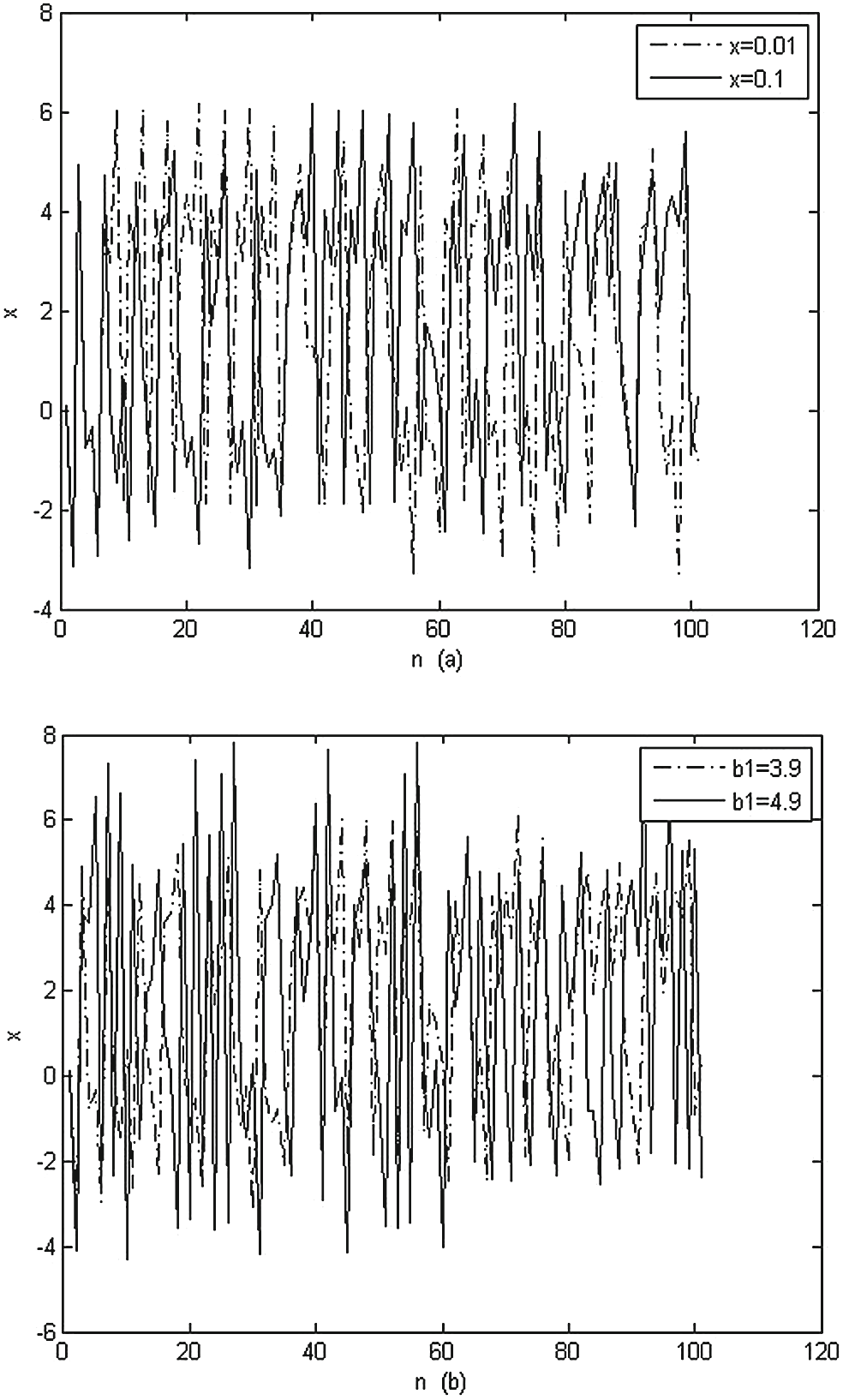映射对初始条件变化的敏感性，针对 x= 0.01, x= 0.1 b 。（）映 射随控制参数变化的轨道图，针对b1= 3.9, b1= 4.9。)

的初始条件在图3（b）中展示。从两幅图中可以看出，它具有

可以看出轨道具有完全的紊乱行为，表现出随时间按指数规律发散。因此，这种特性满足了混淆与扩散等基本密码学要求[16]。

4.2 自相关

伪随机序列应满足戈洛姆公设，例如均匀分布、自相关应类似于δ函数，且序列之间的互相关应为零。自相关函数用于衡量生成的伪随机序列的随机性。混沌序列的自相关特性类似于δ函数， resemble白噪声[16]。图4(a)显示了生成的伪随机序列的自相关函数，图4(b)显示了两个序列之间的互相关，其值近似为零，意味着这两个伪随机序列相互独立。因此，可以利用混沌映射生成的伪随机序列逐个加密明文。

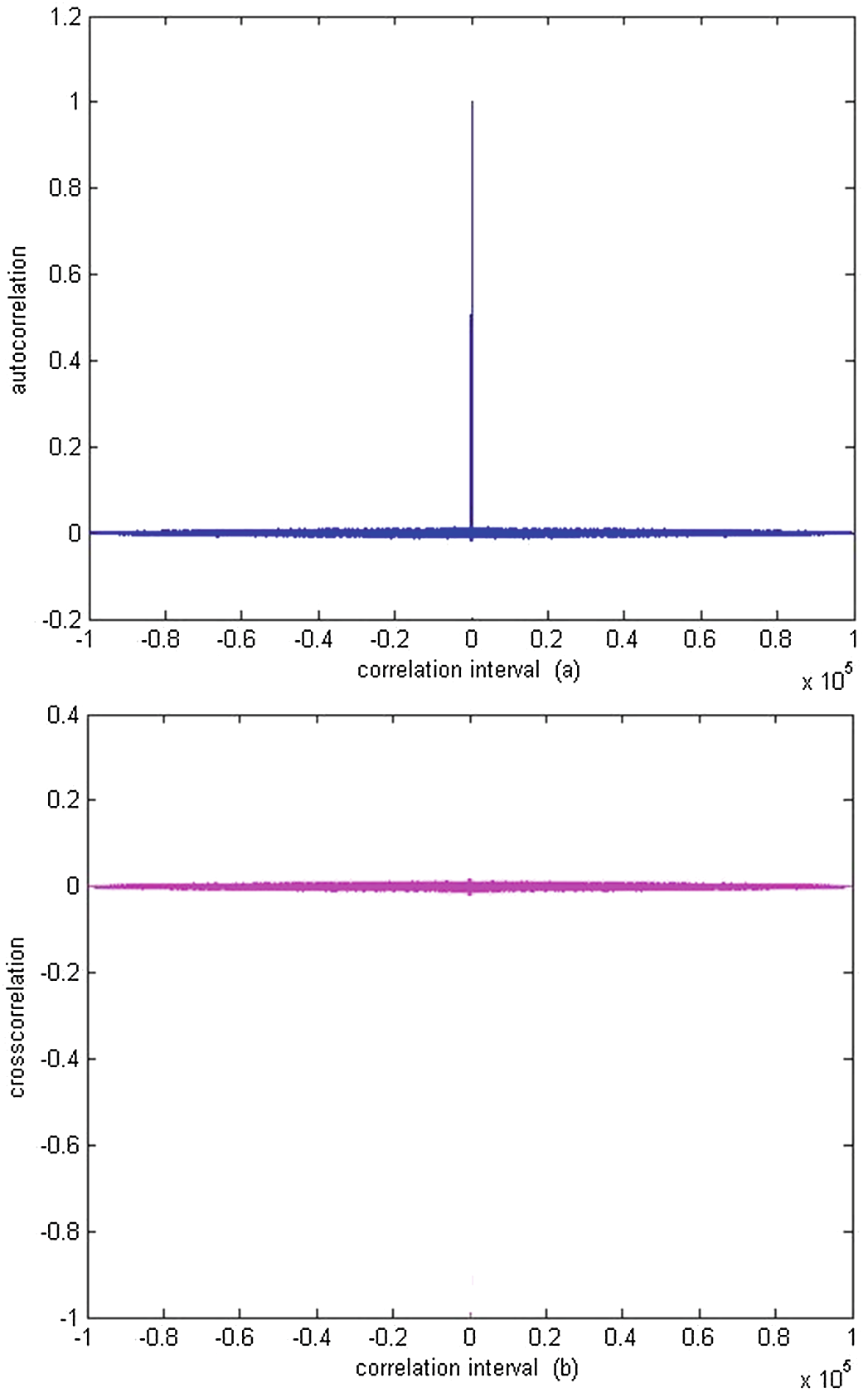x序列的自相关函数。(b) x与 y序列之间的互相关。)

4.3 该映射在图像加密中的应用

混沌映射的一个潜在应用是在安全图像加密中，本文将其作为案例研究。加密过程可分为三个阶段：原始图像的置乱、打乱后的图像扫描以及异或操作。

步骤1 ：使用正弦映射（SM）对原始图像进行置乱，其定义为[4]
zn+1= rsin(πzn) (5)
其中 r表示系统参数和 z ∈[0, 1]。研究结果表明，当 r> 0时可以获得混沌行为。移位和模运算用于混淆像素的值。

步骤2 ：使用扫描机制改变像素位置。在打乱的图像中，像素值按螺旋式读取，如图 5(a)所示。

步骤3 ：扫描后的图像与由改进的Henon映射生成的密钥进行按位异或，这可以提高效率[13]。

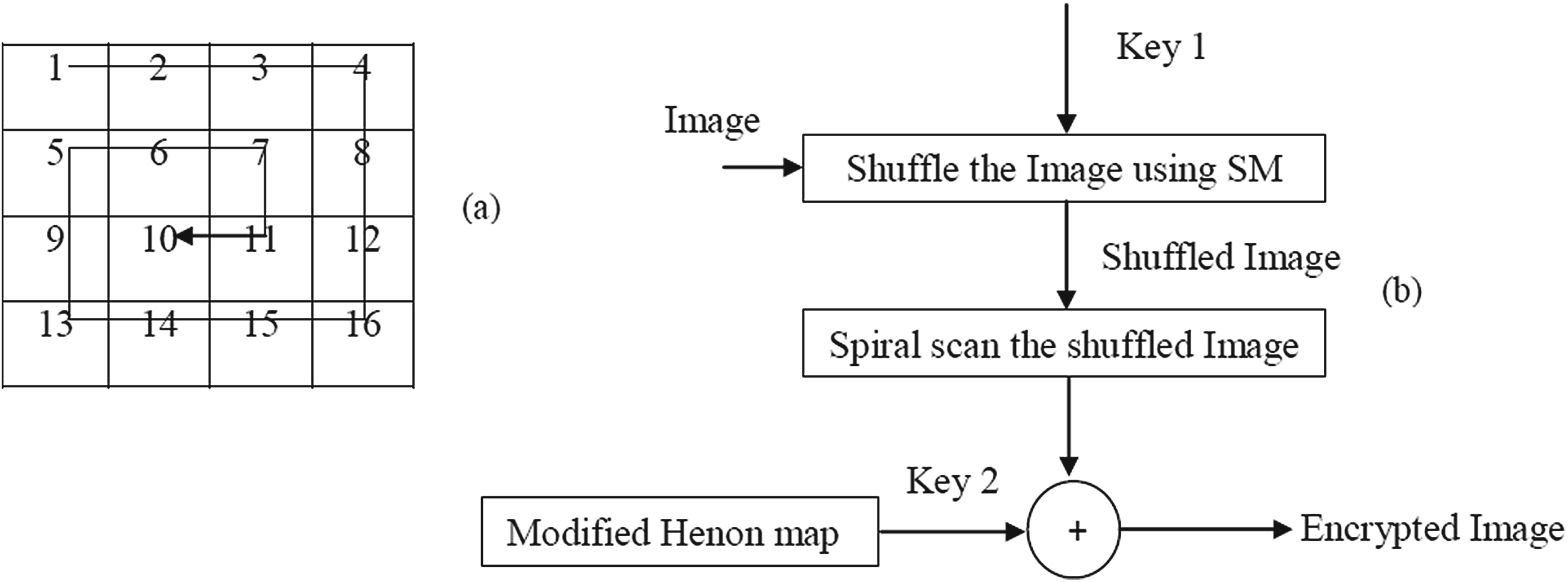螺旋扫描。 (b) 图像加密方案的框图。)
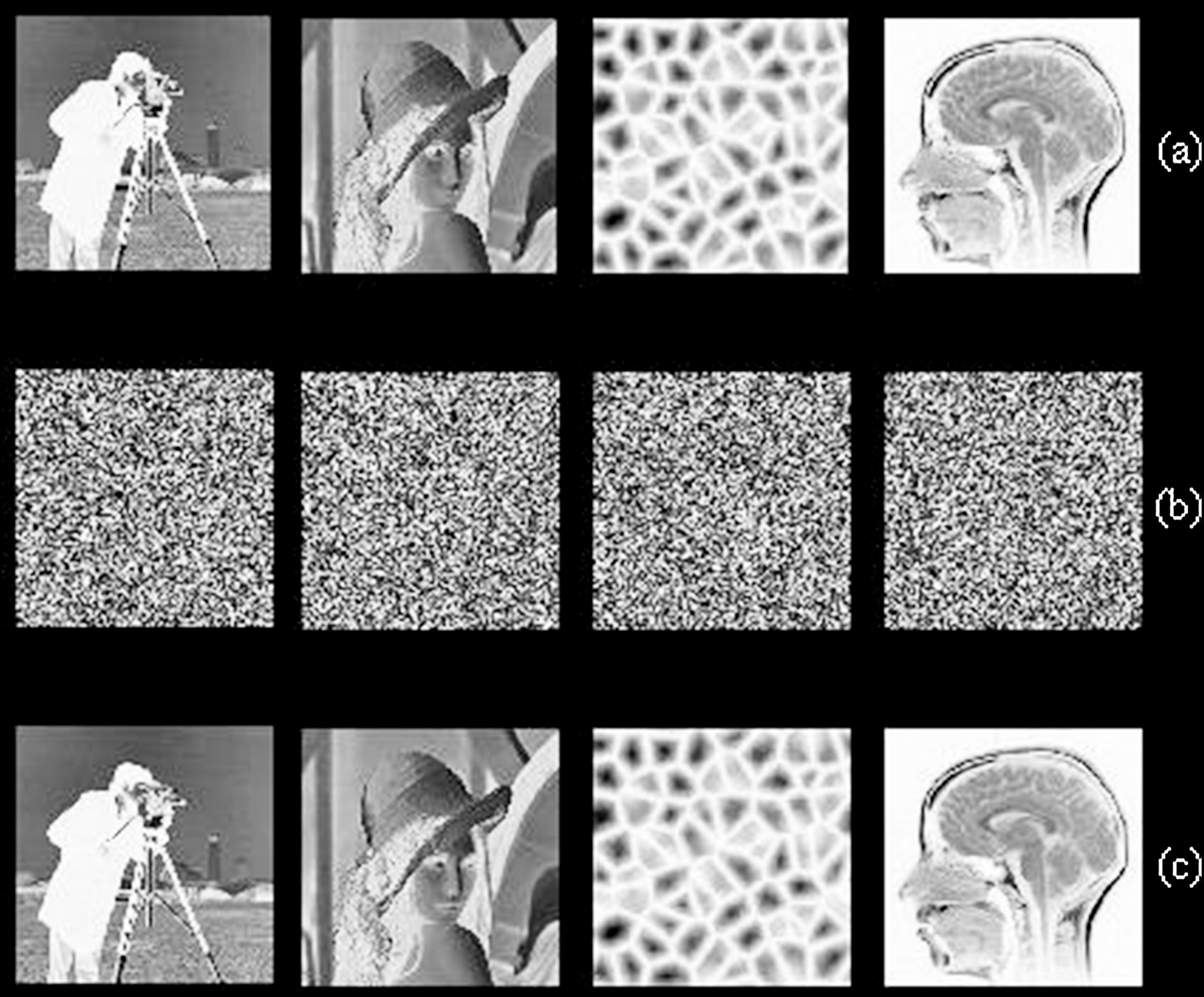明文图像。(b) 加密图像。(c) 解密图像。)

5 安全分析

在本节中，通过使用一些统计测试来评估加密算法的性能，例如明文图像和加密图像的直方图、不同方向上像素间的相关系数、密文图像的像素变化率（NPCR）、统一平均变化强度（UACI）、通用图像质量指数（UIQ）、结构相似性指数度量（SSIM）等。

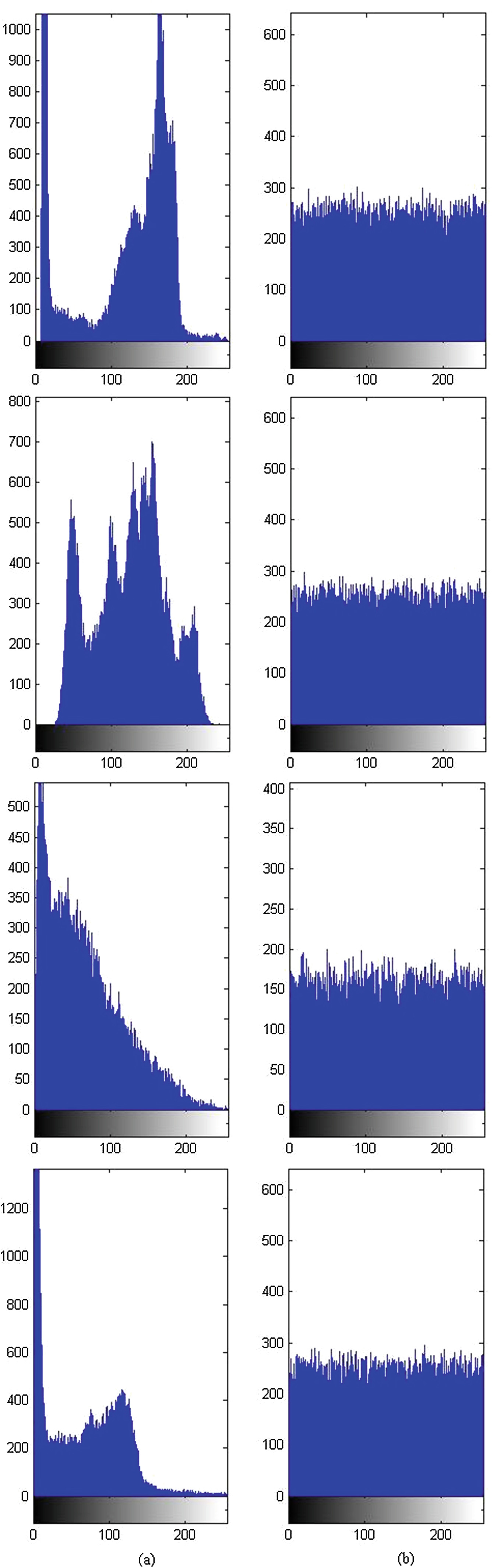
5.1 直方图分析

直方图分析可对任何加密算法进行定性评估。图7展示了若干明文图像及其对应密文图像的直方图。观察发现，由于密文图像的像素分布较为均匀，与原始图像的分布明显不同，因此明文图像与密文图像之间的统计相似性非常低。因此，该算法能够抵抗已知明文攻击。

5.2 相关系数分析

在本小节中，分析了不同明文图像及其对应的加密图像在各个方向上相邻像素之间的相关性。图8展示了明文图像和加密图像在水平、垂直和对角线方向上的相关性分布。表2列出了不同图像在不同方向上的相关系数。观察发现，明文图像中相邻像素之间具有较高的相关性，而密文图像中相关性较低。与现有方法相比，该方法的相关系数更小，如表3所列。因此，所提出的方法在抵抗统计攻击方面表现良好。通过采用复杂的置乱过程，可以进一步改善不同方向的相关系数。相关系数rxy是通过[10]使用公式(6)计算的。

$$
E(x)= \frac{1}{T} \sum_{i=1}^{T} x_i \
D(x)= \frac{1}{T} \sum_{i=1}^{T}(x_i - E(x_i))^2 \
cov(x, y)= \frac{1}{T} \sum_{i=1}^{T}(x_i - E(x_i))(y_i - E(y_i)) \
r_{xy}= \frac{cov(x,y)}{\sqrt{D(x)D(y)}}
$$

图像中两个相邻像素的灰度值分别用x和 y表示，E(x)为均值，均方差用 D(x)表示，cov(x, y)为像素间的协方差。

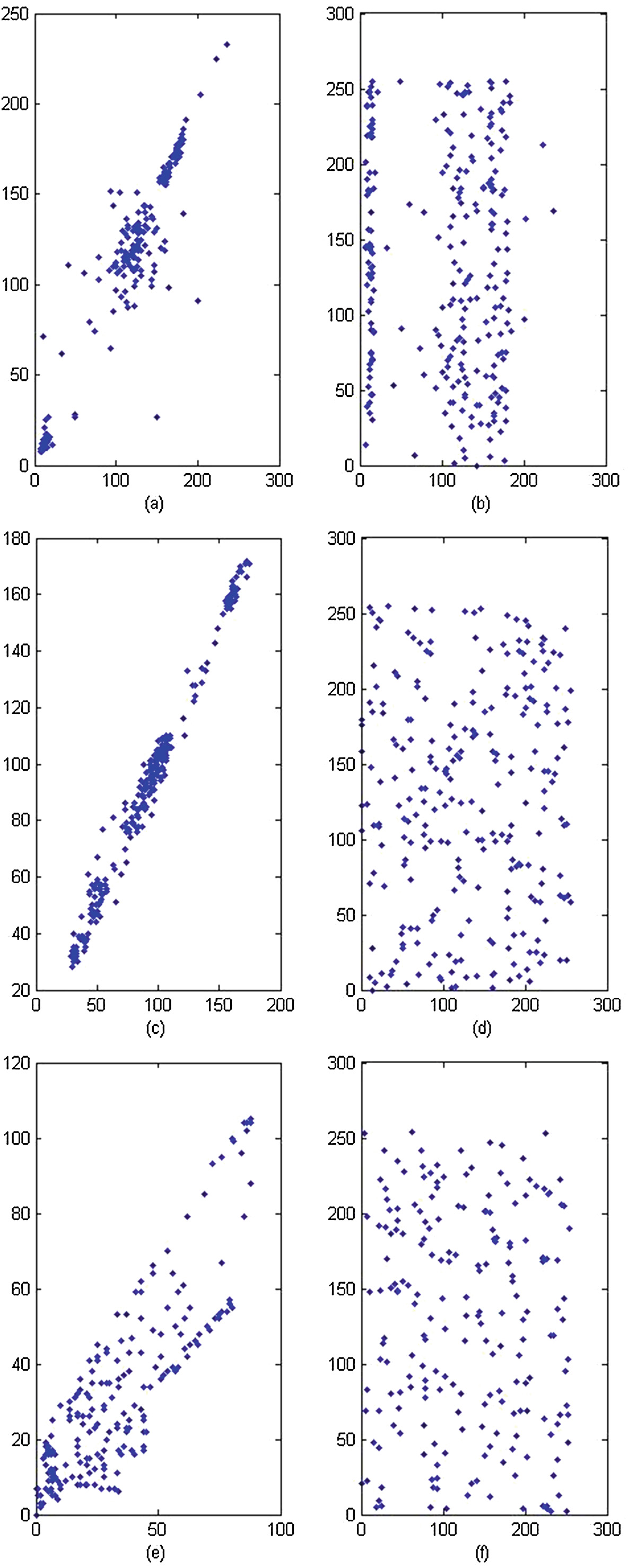Cameraman明文图像在对角线方向的相关性图。(b) Cameraman密文图像在对角线方向的相关性图。(c) Lena明文图像在水平方向的相关性图。(d) Lena密文图像在水平方向的相关性图。(e) 纹理明文图像在垂直方向的相关性图。(f) 纹理密文图像在垂直方向的相关性图。)

5.3 差分分析

任何加密算法的理想特性之一是能够抵抗差分攻击。NPCR和UACI用于衡量原始图像与密文图像之间的差异。NPCR用于测量明文图像与加密图像之间像素位置的灰度值关系，而UACI则专注于测量原始图像与密码图像之间的平均强度变化[10]。不同图像的NPCR和UACI值如表4所示，表明这些值接近理论值。所提出的算法提供的较高NPCR值表明像素值被随机化得更加混乱。该方法与现有算法的比较见表5。使用所提出的方法对Lena图像得到的NPCR和UACI值分别为99.6338%和28.7153%。与文献[11,12]中提出的技术相比，所提出的算法具有更优的NPCR和UACI值。所提出的方法能够有效抵抗明文攻击和差分攻击。然而，UACI值仍有进一步提升的空间，可通过采用复杂扩散机制来实现。

5.4 通用图像质量指数和结构相似性指数

UIQ 和 SSIM 是用于衡量两幅图像之间结构相似性的两个参数，其值范围从 −1到 1[17,18]。当值越接近 1 时，表示图像之间的相似性越高。不同图像的 UIQ 和 SSIM 值如表4所示。从表中可以看出，由于数值并不接近 1，因此图像之间没有明显的相似性。

5.5 熵分析

任何加密算法的强度都通过信息熵来衡量，信息熵表示系统中的随机性程度[1]。对于8位消息，假设有256种可能结果且每个结果出现的概率相等，则理想熵值应等于8。一个良好的加密算法的信息熵应接近理想值，这意味着在加密过程中信息泄露可以忽略不计。部分图像及其密文图像的信息熵如表2所示，其值非常接近理想值。该算法与其他算法在熵方面的比较见表5。从表中可以看出，与[11]中提出的其他算法相比，该方法的密文不确定性更高。尽管提出的算法能够抵抗熵攻击，但在熵值方面仍有改进空间。可以通过提高由混沌映射生成的密钥的随机性，或采用更复杂的置乱与扩散机制来实现改进[14]。

5.6 关键敏感性分析

为了实现高安全性，任何加密算法都应对原始图像的微小变化高度敏感，并且密钥的微小改变应在加密图像中引起巨大变化。为证明这一点，通过轻微改变其中一个系统参数，对解密过程进行密钥敏感性测试。正确密钥集包含的参数值为 x0= 0.1, y0= 0.775, b1= 3.85, b2=0.5，而轻微修改的密钥为 x0= 0.1, y0= 0.775, b1= 3.85, b2= 0.50000001。使用正确密钥解密的图像如图9(b)所示，而使用轻微修改的密钥解密得到的对应图像如图9(c)所示。因此，提出的算法在使用轻微修改的密钥时会产生完全不同的解密图像。

此外，密钥敏感性测试还通过一次改变一个参数的微小变化来进行。原始密钥集被修改，从而生成四组不同的密钥集。敏感性测试的性能通过NPCR和UACI参数进行衡量，结果列于表6中。从表中可以看出，NPCR和UACI值接近理想值，提出的算法对密钥具有高敏感性。

原始图像。 (b) 使用正确密钥解密的图像。 (c) 使用轻微修改的密钥解密的图像。)

5.7 雪崩效应

任何加密算法的理想特性是衡量密钥或明文的微小变化对密文的影响。雪崩效应通过依次略微改变密钥集中的一个参数来测量，结果列于表6中。从表中可以看出，密钥集的微小变化导致了更多像素值发生变化，表明改进的Henon映射提供了更高的安全性。

6 结论

大密钥空间、对初始条件/系统参数的敏感性以及广泛的混沌区域是混沌密码学中的关键方面，推动了能够满足安全需求的混沌映射的发展。在这方面，本文通过解析方法和仿真对改进的Henon映射进行了研究。研究表明，该映射在较宽范围的系统参数下均存在混沌区域，且其统计特性与白噪声相似。此外，通过使用改进的Henon映射和正弦映射进行图像加密，并结合安全性分析，验证了混沌映射在图像加密中的应用。结果表明，该算法在NPCR、UACI、UQI、SSIM等方面具有良好的安全性，可用于可靠的图像加密。与其他算法相比，在相关系数、熵、NPCR和UACI等方面，该算法也能有效抵抗各种典型攻击。

表1. 映射分岔图中的不同区域。
b1
0 ≤ b1 ≤ 1.5
1.5 ≤ b1 ≤ 2.19
2.19 ≤ b1 ≤ 2.5
2.5 ≤ b1 ≤ 2.54
b1 > 2.54

表2. 不同图像的相关系数和熵
图像
Lena
纹理
摄影师
医学

表3. Lena图像的相关系数比较。
水平
垂直
对角线

表4. 差分分析。
图像
Lena (256× 256)
纹理 (204× 204× 3)
摄影师 (256× 256)
医学 (256× 256)

表5. 提出的算法与其他算法的NPCR和UACI比较。
NPCR
UACI
熵

表6. 密钥敏感性分析。
密钥集
x0= 0.10000001, y0= 0.775, b1= 3.85, b2= 0.5
x0= 0.1, y0= 0.77500000001, b1= 3.85, b2= 0.5
x0= 0.1, y0= 0.775, b1= 3.85000001, b2= 0.5
x0= 0.1, y0= 0.775, b1= 3.85, b2= 0.5000000001