REINFORCE、Remax、GRPO、DR.GRPO、DAPO、REINFORCE++、VC-PPO、VAPO对比

taoqick

已于 2025-07-15 10:18:18 修改

阅读量196

点赞数 3

CC 4.0 BY-SA版权

文章标签：人工智能深度学习

于 2025-07-04 20:30:50 首次发布

本文链接：https://blog.youkuaiyun.com/taoqick/article/details/149124598

REINFORCE

REINFORCE算法使用蒙特卡罗方法计算策略梯度，智能体根据当前策略与环境交互，生成一条状态-动作-奖励序列（轨迹）。对每条轨迹进行回报计算，通常采用折扣累计奖励（也就是下图中的r）的形式。REINFORCE的缺点就是方差大，按照论文ReMax: A Simple, Effective, and Efficient Reinforcement Learning Method for Aligning Large Language Models里的说法就是In theory, this variance can be attributed
to two main sources: the external randomness inherent in
MDP’s transitions and the internal randomness from the
policy decisions of the language model (i.e., token generation).
在这里插入图片描述

ReMax（REINFORCE+argmax）

来自ReMax: A Simple, Effective, and Efficient Reinforcement Learning Method for Aligning Large Language Models。在REINFORCE基础上加个baseline，放弃critic函数，This baseline value can be obtained by greedily sampling a
response and calculating the associated reward value
在这里插入图片描述
在VeRL论文（HybridFlow: A Flexible and Efficient RLHF Framework）中，ReMax被描述成了一个需要Actor Gen两次的数据流，因为baseline确实多采样了一次

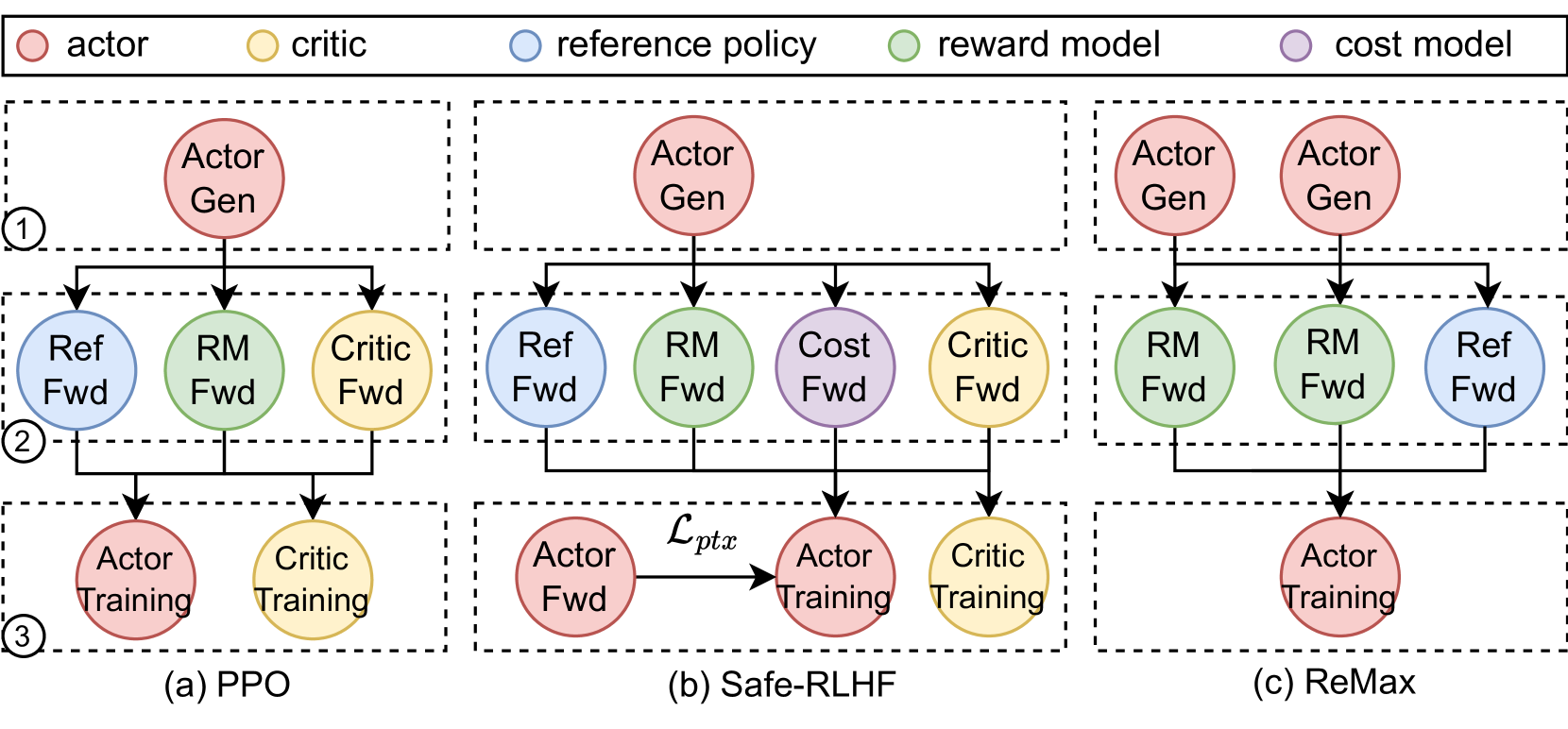
来看一下VeRL中Remax advantage的实现：

@register_adv_est(AdvantageEstimator.REMAX)  # or simply: @register_adv_est("remax")
def compute_remax_outcome_advantage(
    token_level_rewards: torch.Tensor,
    reward_baselines: torch.Tensor,
    response_mask: torch.Tensor,
    config: Optional[AlgoConfig] = None,
    **kwargs,
) -> tuple[torch.Tensor, torch.Tensor]:
    """
    Compute advantage for ReMax, operating only on Outcome reward
    This implementation is based on the paper: https://arxiv.org/abs/2310.10505
    (with only one scalar reward for each response).

    Args:
        token_level_rewards: `(torch.Tensor)`
            shape: (bs, response_length)
        reward_baselines: `(torch.Tensor)`
            shape: (bs,)
        response_mask: `(torch.Tensor)`
            shape: (bs, response_length)
        config: (AlgoConfig) algorithm config

    Returns:
        advantages: `(torch.Tensor)`
            shape: (bs, response_length)
        Returns: `(torch.Tensor)`
            shape: (bs, response_length)
    """

    with torch.no_grad():
        returns = (token_level_rewards * response_mask).flip(dims=[-1]).cumsum(dim=-1).flip(dims=[-1])
        advantages = returns - reward_baselines.unsqueeze(-1) * response_mask

    return advantages, returns

问题1：为什么减去Baseline对于Policy-Gradient来说是无偏的?

减去基线的操作是将梯度修改为：
$\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \left( R(\tau) - b \right) \nabla_\theta \log \pi_\theta(\tau) \right]$
其中b是基线（通常为状态值函数 $(V (s)$ )）。关键问题在于：为何这种修改不引入偏差？

无偏性的数学本质

无偏性要求修改后的梯度期望值与原梯度一致：
$\mathbb{E}_{\tau \sim \pi_\theta} \left[ \left( R(\tau) - b \right) \nabla_\theta \log \pi_\theta(\tau) \right] = \mathbb{E}_{\tau \sim \pi_\theta} \left[ R(\tau) \nabla_\theta \log \pi_\theta(\tau) \right]$

只需证明基线项期望为零：
$\mathbb{E}_{\tau \sim \pi_\theta} \left[ b \cdot \nabla_\theta \log \pi_\theta(\tau) \right] = 0$

证明过程

期望的分解：
利用期望的线性性质：
$\mathbb{E}_{\tau} \left[ b \nabla_\theta \log \pi_\theta(\tau) \right] = b \cdot \mathbb{E}_{\tau} \left[ \nabla_\theta \log \pi_\theta(\tau) \right]$
对数梯度的期望为零：
$\mathbb{E}_{\tau} \left[ \nabla_\theta \log \pi_\theta(\tau) \right] = \int \pi_\theta(\tau) \nabla_\theta \log \pi_\theta(\tau) d\tau = \int \nabla_\theta \pi_\theta(\tau) d\tau = \nabla_\theta \int \pi_\theta(\tau) d\tau = \nabla_\theta (1) = 0$
这里的关键步骤是交换积分与微分顺序（需满足一定正则条件），并利用概率密度积分为1的性质。

问题2：为什么减去Baseline能降低方差？

尽管基线不影响无偏性，但能显著降低梯度估计的方差：

直观解释：若 $R(τ)R(\tau)$ 整体偏移一个常数b，其相对差异（如 $R(τ)R(\tau)$ - b ）的波动范围更小。
最优基线选择：理论证明，当 $\mathbb{E}[R(\tau)^2 \| \nabla \log \pi_\theta \|^2] / \mathbb{E}[\| \nabla \log \pi_\theta \|^2]$ 时方差最小。实践中常用 ( b = V(s) )（状态值函数），因其与奖励尺度匹配。

示例说明：假设两条轨迹的奖励和梯度：

(\tau_1)：( R(\tau_1)=10 )，(\nabla \log \pi_\theta = 0.5)
(\tau_2)：( R(\tau_2)=20 )，(\nabla \log \pi_\theta = 0.5)
若取基线 ( b = 15 )，则修正后奖励为 ([-5, 5])，梯度估计为 ([-2.5, 2.5])，方差远小于原始值 ([5, 10])。

GRPO （Group Relative Policy Optimization）

在这里插入图片描述

价值网络的使用

PPO：依赖于一个与Policy Model大小相当的价值网络（critic model）来估计优势函数（advantage function）。这个价值网络需要在每个时间步对状态进行评估，计算复杂度高，内存占用大。
GRPO：完全摒弃了价值网络，通过组内相对奖励来估计优势函数。这种方法通过比较同一状态下的多个动作的奖励值来计算相对优势，显著减少了计算和存储需求。

奖励计算方式

GPRO的loss公式为，其中G为G个长短不一的prompts，每个序列的长度为 $o_i|$
$gradA^i,t−βDKL[πθ∥πref]] \mathcal{L}_{\mathrm{GRPO}}(\theta) = -\frac{1}{\sum_{i=1}^G |o_i|} \sum_{i=1}^G \sum_{t=1}^{|o_i|} \left[ \frac{ \pi_\theta(o_{i,t} \mid q, o_{i,<t}) }{ [\pi_\theta(o_{i,t} \mid q, o_{i,<t})]_{\mathrm{no\ grad}} } \hat{A}_{i,t} - \beta \mathbb{D}_{\mathrm{KL}}\left[ \pi_\theta \| \pi_{\mathrm{ref}} \right] \right]$

PPO：使用广义优势估计（GAE）来计算优势函数，需要对每个动作的即时奖励和未来奖励的折扣总和进行估计。
GRPO：通过采样一组动作并计算它们的奖励值，然后对这些奖励值进行归一化处理，得到相对优势。这种方法更直接，减少了对复杂奖励模型的依赖。
- 在huggingface的trl库中，PPO执行一次采样多次更新，而GRPO一次采样后只进行一次策略更新，因此新旧策略是在这种情况下是相同的 $πθ=πθold\pi_{\theta}=\pi_{\theta}^{old}$ ，因此这种情况下都可以去掉clip函数，也就是上面公式A前面的系数为1。在实际训练中，通常会发现前期的loss一直为0，这是因为前期KL散度接近于0

使用Reverse KL

PPO：通过裁剪概率比（clip operation）来限制策略更新的幅度，确保策略分布的变化在可控范围内。
GRPO：引入了KL散度约束，直接在损失函数中加入Reverse KL，从而更精细地控制策略更新的幅度。MiniLLM: Knowledge Distillation of Large Language Models论文中的观点，Reverse KL更好地拟合teacher模型的峰值，如图中绿色线，而forward KL趋向于拟合均值，如图中橙色线。
- 对于正向KL，从 $dx\int_x p(x) \log \frac{p(x)}{q(x)} \, dx$ 公式来看，如果想用q来拟合p，那么在p大的地方，q也应该大才行；在p小的地方，q也应该尽量不为0，因此正向KL散度被称为是zero avoiding (mean seeking)。
- 对于反向KL，还是想用q来拟合p，从 $dx\int_x q(x) \log \frac{q(x)}{p(x)} \, dx$ 公式来看，在p小的位置，q也应该尽量小，所以反向KL也被叫做zero forcing (mode seeking)，也就是说在teacher模型较低的位置，学生模型也会分配较低的概率，虽然遗失了较多长尾分布，但是保证有较好的事实性和低幻觉

RLOO（REINFORCE Leave-One-Out）

来自Back to basics: Revisiting reinforce style optimization for learning from human
feedback in llms，和GRPO流程大致相同，只是GRPO是用组内平均作为baseline，在RLOO中是使用Leave One Out（也就是说出去当前奖励的其他平均奖励）作为baseline，下图公式直接摘录自REINFORCE++论文：
$Aq,ot(i)=r(o1:T(i),q)−1k−1∑j≠ir(o1:T(j),q)A_{q, o_t^{(i)}} = r(o_{1:T}^{(i)}, q) - \frac{1}{k-1} \sum_{j \neq i} r(o_{1:T}^{(j)}, q)$

DAPO （Dynamic sAmpling Policy Optimization）

DAPO可以看成是对GRPO的改进，主要有四点：

Entropy collapse，熵变小，模型探索性不足，解决方案是CLIP Higher，也就是说把上下界给解耦，给低概率的token增加留出更多的空间，从而避免熵崩溃。
解决了GRPO中训练效率和稳定性，也就是说在训练过程中，当某些输入的准确率是1/0, 这些样本对梯度没贡献了。所以DAPO的采样过滤掉这些样本，确保每个批次样本都能有效贡献梯度。（持续采样，直到满足采样条件，叫做Dynamic Sampling）
解决了GRPO中原始loss使用样本级别的loss计算，在DAPO中改成了Token Level Policy Gradient Loss
Overlong reward shaping: 在强化学习训练中，过长的样本可能会被截断，这个截断的样本会引入奖励噪声，作者们提出了2个策略来应对，一个是直接屏蔽截断样本的损失，其次是对超过预设长度的样本施加惩罚

REINFOCE++

来自于REINFORCE++: An Efficient RLHF Algorithm with Robustness to Both Prompt and Reward Models，作者有两个观点：

1)PPO执行一次采样多次更新（单个query的采样组为对象计算baseline）；2)而GRPO一次采样后只进行一次策略更新（以单个query的采样组responses为单位进行优势函数的估计，token的优势函数值多样性较低）；3)Remax一个query采样2次得到 $r_{sample}$ 和 $r_{greedy}$ 进行价值更新；4)但在REINFOCE++中，改成了n个queries得到n个responses作为一组计算优势值
Token-Level KL Penalty：REINFORCE++计算的是token级别的KL散度，而非全句子级别的，相当于实现了PPO中KL Reward的Credit Assignment，本质上与GRPO中直接把KL散度作为Loss的作用一致。优势函数如下所示：
$KL(t)=log⁡(πθold(at∣st)/πref(at∣st))A_{q,o_{t}}=r(q,o_t)-\beta\cdot\sum_{i=t}^{T}\mathrm{KL}(i)，\text{where} \space KL \left( t \right)= \log \left( \pi_{ \theta_{old}} \left( a_{t}|s_{t} \right)/ \pi_{ref} \left( a_{t}|s_{t} \right) \right)$
总体来说，REINFORCE++ 比 GRPO 更稳定，速度比PPO更快