85.最大矩形 python

题目

题目描述

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

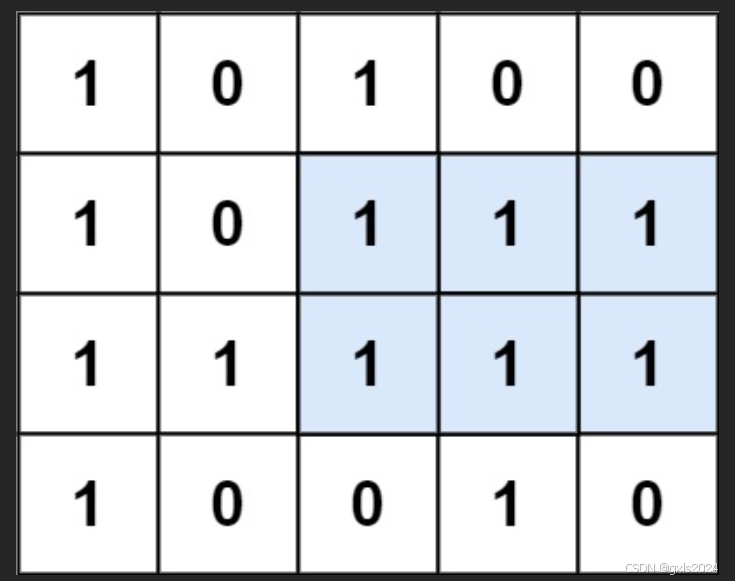
输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = [[“0”]]
输出：0

示例 3：

输入：matrix = [[“1”]]
输出：1

提示：

rows == matrix.length
cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] 为 ‘0’ 或 ‘1’

题解

这个问题被称为“最大矩形问题”，它可以通过将每一行视为柱状图的底，然后计算每个柱状图中最大的矩形面积来解决。具体来说，我们可以使用动态规划（Dynamic Programming, DP）的方法来构建高度数组，并利用之前提到的“柱状图中最大的矩形”算法来计算每行的最大矩形面积。

解题思路

1. 初始化：创建一个与矩阵列数相同长度的高度数组 heights，用于存储当前行及其以上连续 ‘1’ 的数量。
2. 遍历每一行：
   • 对于每一行中的每一个元素，更新 heights 数组。如果当前元素是 ‘1’，则在对应位置的高度加 1；如果是 ‘0’，则重置为 0。
3. 调用辅助函数：对于每一行更新后的 heights 数组，调用一个辅助函数 largestRectangleArea 来计算该行作为底部时的最大矩形面积。
4. 记录最大值：在每次调用 largestRectangleArea 后，比较并记录最大面积。

辅助函数 largestRectangleArea

这个辅助函数用于计算给定高度数组所能形成的最大矩形面积。可以参考之前的讨论，使用单调栈方法实现。

Python 实现代码