48.旋转图像 python

题目

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

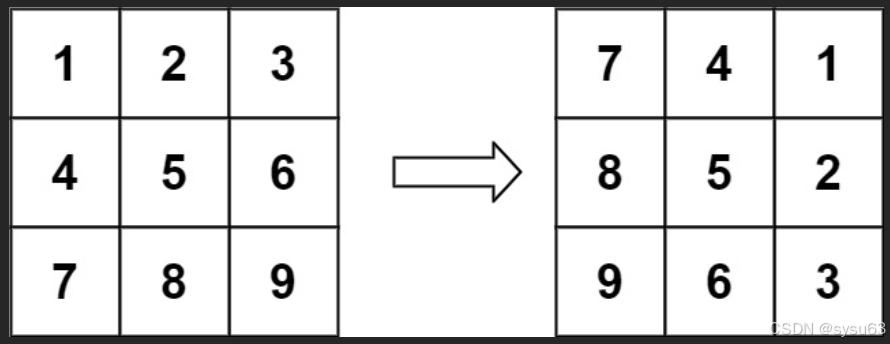
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

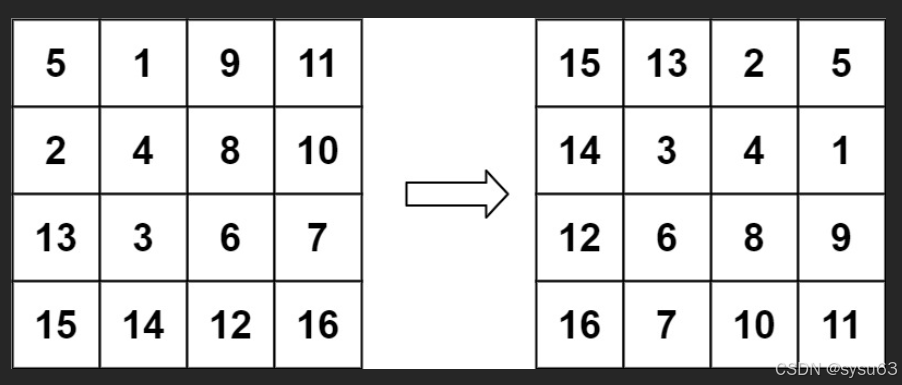
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

题解

解题思路

要将一个 n × n 的二维矩阵顺时针旋转 90 度，我们可以在原地完成这个操作，而不需要额外的空间。实现这个目标的一个有效方法是通过分层交换元素的方式。

算法步骤如下：

1. 分层处理：想象矩阵是由多个层组成的，最外层包含最外边的元素，然后向内一层一层直到中心。每一层都需要进行元素交换来完成旋转。

2. 四角交换：对于每一层中的每个元素，需要进行四角交换，即四个位置上的元素循环移动。例如，第一层的第一个元素会移动到它的右边对应的位置，那个位置的元素会移动到它下面对应的位置，以此类推，直到四个元素都移动到它们新的正确位置上。

3. 逐层深入：当最外层的所有元素都被正确放置后，进入下一层重复上述过程，直到所有层都被处理完毕。

python实现

下面是 Python 实现代码：

def rotate(matrix: List[List[int]]) -> None:
    """
    Do not return anything, modify matrix in-place instead.
    """
    n = len(matrix)
    for layer in range(n // 2):
        first = layer
        last = n - 1 - layer
        for i in range(first, last):
            offset = i - first
            top = matrix[first][i]  # Save top

            # left -> top
            matrix[first][i] = matrix[last-offset][first]

            # bottom -> left
            matrix[last-offset][first] = matrix[last][last - offset]

            # right -> bottom
            matrix[last][last - offset] = matrix[i][last]

            # top -> right
            matrix[i][last] = top  # Right <- saved top

提交结果