Leetcode543. 二叉树的直径

Leetcode543. 二叉树的直径

题目：
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :

给定二叉树

          1
         / \
        2   3
       / \     
      4   5    
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

题解：
深度优先搜索

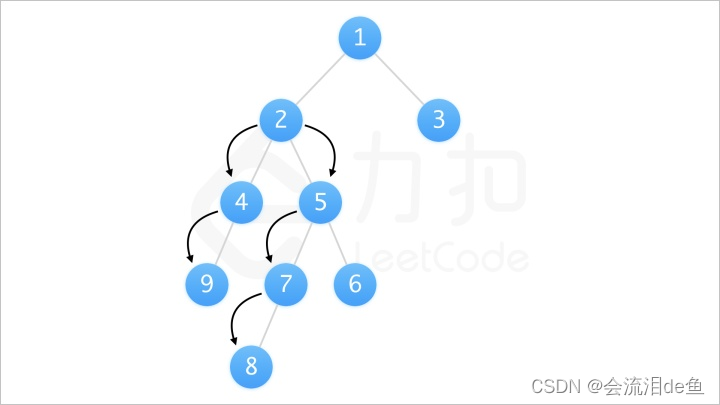
如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 2 为起点，从其左儿子向下遍历的路径 [2, 4, 9] 和从其右儿子向下遍历的路径 [2, 5, 7, 8] 拼接得到。

假设我们知道对于该节点的左儿子向下遍历经过最多的节点数 $L$ （即以左儿子为根的子树的深度） 和其右儿子向下遍历经过最多的节点数 $R$ （即以右儿子为根的子树的深度），那么以该节点为起点的路径经过节点数的最大值即为 $L+R+1$ 。

我们记以节点 $\text{node}$为起点的路径经过节点数的最大值为 $d_{\text{node}}$，那么二叉树的直径就是所有节点 $d_{\text{node}}$的最大值减一。

我们定义一个递归函数$depth(node)$ 计算 $d_{\text{node}}$ ，函数返回该节点为根的子树的深度。先递归调用左儿子和右儿子求得它们为根的子树的深度 $L$ 和 $R$ ，则该节点为根的子树的深度即为$max(L,R)+1$
该节点的 $d_{\text{node}}$值为$L+R+1$，递归搜索每个节点并设一个全局变量 $ans$ 记录 $d_{\text{node}}$的最大值，最后返回 $ans-1$ 即为树的直径。

java代码：

/**
     * @param root
     * @return
     */
    static int ans;

    public static int diameterOfBinaryTree(TreeNode root) {
        ans = 1;
        depth(root);
        return ans - 1;


    }

    private static int depth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int L = depth(root.left);
        int R = depth(root.right);
        ans = Math.max(ans, L + R + 1);
        return Math.max(L, R) + 1;

    }