LeetCode 543.二叉树的直径 C语言

方法一：遍历每个节点的直径取最大值

看到这个题我的第一个反应是遍历二叉树中的每一个节点，求出来以该节点为根的树的直径，然后去其中直径最大的值返回就行

int dia;

int deepth(struct TreeNode* root)
{
    if(!root)
        return 0;
    return fmax(deepth(root -> left), deepth(root -> right)) + 1;
}

void travel(struct TreeNode* root)
{
    if(root)
    {
        int dep = deepth(root -> left) + deepth(root -> right);
        dia = fmax(dia, dep);
        travel(root -> left);
        travel(root -> right);
    }
}

int diameterOfBinaryTree(struct TreeNode* root) {
    dia = 0;
    travel(root);
    return dia;
}

这里的travel函数是对二叉树进行先序遍历每个节点求节点最大直径的

至于最大直径的求法 就是左子树的深度加右子树的深度

需要注意的是题目中给的直径的定义是

        树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

        两节点之间路径的 长度 由它们之间边数表示。

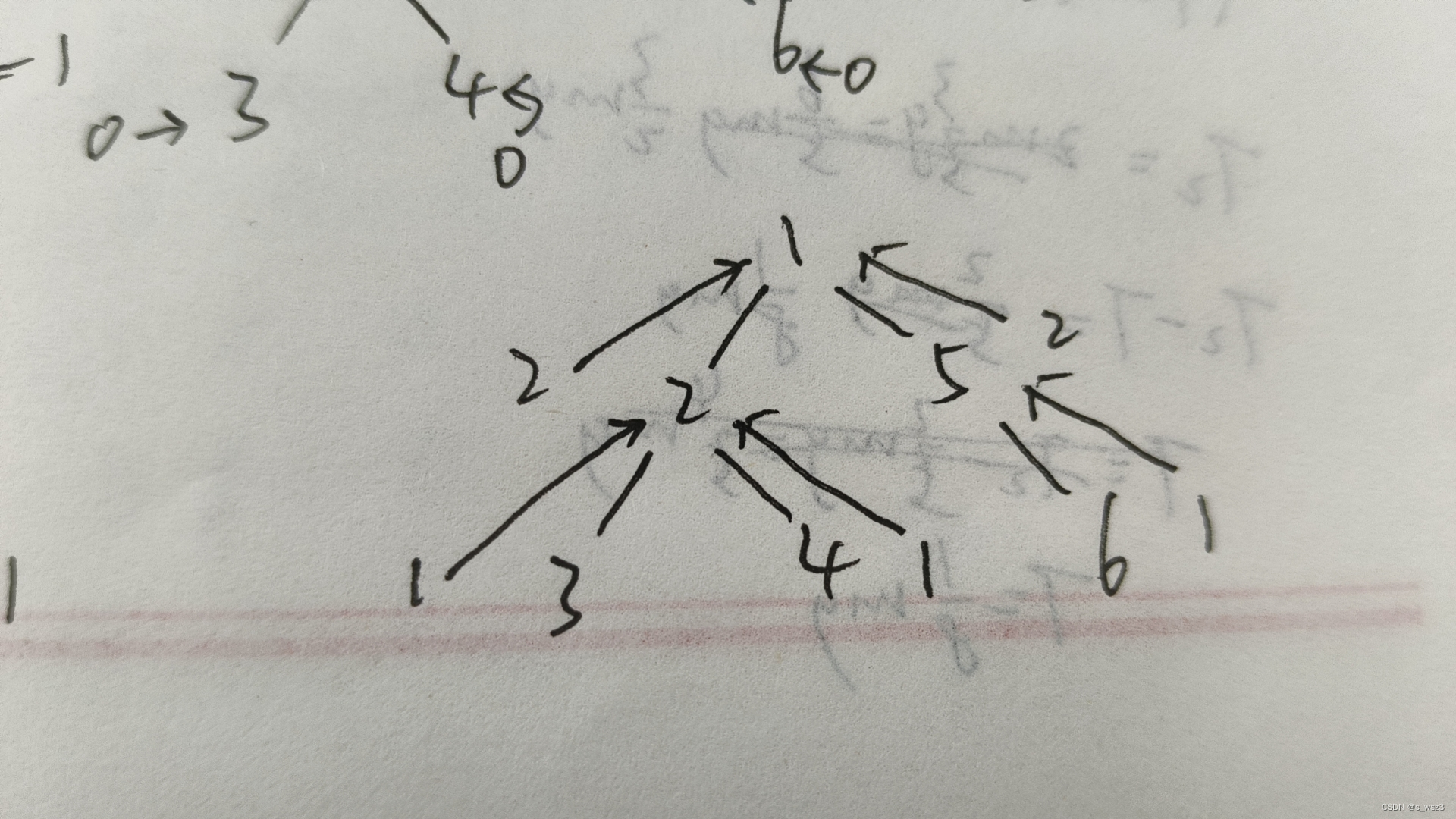
如上图 子树返回的深度恰好等于子树的最高的路径的边的数量加上根节点到子树的那一条边

比如说根为1的树 左子树最高的路径就是2到3或者2到4 边数为1 再加上2到1的那一条边 就是1+1=2就等于左子树的高度

这样一来每求出一个节点的最大直径就和已经访问过的节点中最大的直径比较 不断更新dia的值就能得到树的最大直径

方法二：

方法一比较好想，但每访问一个节点 就要遍历以节点为根的子树 时间复杂度就达到了n平方 有没有更省时的方法呢？

我们可以自下而上遍历树 返回每棵树的深度 这样每回到上一层递归函数直接得到了子树的深度 再通过与当前最大直径的比较就能得出树的最大直径

int max;

int DFS(struct TreeNode* root)
{
    if(!root)
        return 0;
    int left = DFS(root -> left);
    int right = DFS(root -> right);
    max = fmax(max, left + right);
    return fmax(left, right) + 1;
}

int diameterOfBinaryTree(struct TreeNode* root) {
    max = 0;
    DFS(root);
    return max;
}

其中max作为全局变量位于内存全局区 不会随函数在栈区的递归调用而改变

需要注意的是DFS返回值是当前树的最高路径的长度 而不是当树的最大直径