前言
前三题相对于第四题来说比较简单,NOIP2015提高组
JZOJ 3027 计算系数
题目
给定一个多项式 ( a x + b y ) k (ax+by)^k (ax+by)k,请求出多项式展开后 x n y m x^ny^m xnym项的系数。
分析
根据二项式定理,就可以得到 c ( k , n ) a n b m c(k,n)a^nb^m c(k,n)anbm就是它的系数,所以说快速幂+费马小定理解决
JZOJ 3025 选择客栈
题目
有多少个区间,满足第一个和最后一个的颜色相同,且该区间含有 ≤ p \leq p ≤p的地方
代码
#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
struct col{int hav,nav,hum,num;}a[51];//分别表示前一个有客栈的店,从头到该店的同颜色数量,最后一个同颜色的店,从头到该店的同颜色数量
int n,k,p,ans;
inline signed iut(){
rr int ans=0; rr char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) ans=ans*10+c-48,c=getchar();
return ans;
}
signed main(){
n=iut(); k=iut(); p=iut();
for (rr int i=1;i<=n;++i){
rr int colo=iut()+1,pay=iut();
a[colo].hum=i,++a[colo].num;
if (pay<=p)
for (rr int t=1;t<=k;++t)
a[t].hav=a[t].hum,a[t].nav=a[t].num;
ans+=a[colo].nav;
if (a[colo].hav==i) --ans;
}
return !printf("%d",ans);
}
JZOJ 3028 聪明的质检员
分析
那么这道题很容易发现就是二分W,之后怎么做呢,分块,可以求符合要求的前缀和(个数和价值和),然后对于每个区间用区间减的方式实现,这样就可以求出答案,时间复杂度
O
(
(
n
+
m
)
l
o
g
n
)
O((n+m)logn)
O((n+m)logn)。
代码
#include <cstdio>
#include <cctype>
#include <algorithm>
#define rr register
using namespace std;
const int N=200011; struct rec{int w,v;}a[N];
int n,m,l[N],r[N],c[N],d[N]; long long b[N],stdd;
inline signed iut(){
rr int ans=0; rr char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) ans=ans*10+(c-48),c=getchar();
return ans;
}
inline long long check(int mid){
rr long long ans=-stdd;
for (rr int i=1;i<=n;++i) b[i]=b[i-1]+a[i].v*(a[i].w>=mid);
for (rr int i=1;i<=n;++i) c[i]=c[i-1]+(a[i].w>=mid);
for (rr int i=1;i<=m;++i) ans+=(b[r[i]]-b[l[i]-1])*(c[r[i]]-c[l[i]-1]);
return ans;
}
signed main(){
n=iut(); m=iut(); scanf("%lld",&stdd);
for (rr int i=1;i<=n;++i) a[i]=(rec){iut(),iut()};
for (rr int i=1;i<=m;++i) l[i]=iut(),r[i]=iut();
for (rr int i=1;i<=n;++i) d[i]=a[i].w;
sort(d+1,d+1+n); rr int tt=unique(d+1,d+1+n)-d-1;
rr int L=1,R=tt+1; rr long long minx=1e18;
while (L<R){
rr int mid=(L+R)>>1; rr long long t=check(d[mid]);
if (t<=0) R=mid; else L=mid+1; t=t<0?-t:t;
minx=minx<t?minx:t;
}
return !printf("%lld",minx);
}
JZOJ 3029 观光公交
分析
其实这是一道费用流的题目
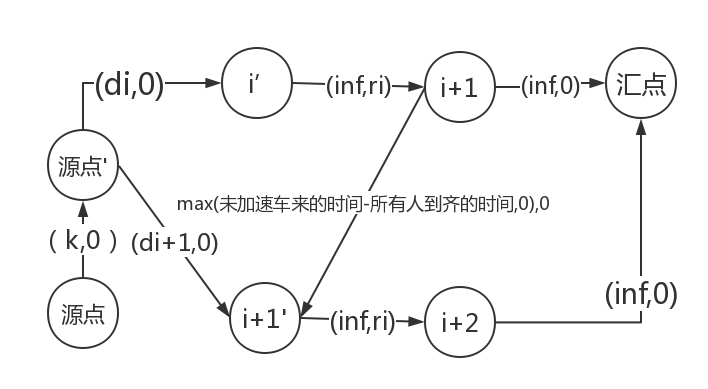
r
i
ri
ri表示在这一站下车的人数(代码丑陋,就不放了)
后续
NOIP2011提高组
洛谷 1313 计算系数
洛谷 1311 选择客栈
洛谷 1314 聪明的质检员
洛谷 1315 观光公交








 本文深入解析了NOIP2015提高组的四道算法题:计算系数、选择客栈、聪明的质检员及观光公交。通过二项式定理、费马小定理、分块技术和费用流算法,详述了解题思路与代码实现。
本文深入解析了NOIP2015提高组的四道算法题:计算系数、选择客栈、聪明的质检员及观光公交。通过二项式定理、费马小定理、分块技术和费用流算法,详述了解题思路与代码实现。
















 546
546

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








