VINS_FUSION采用全局融合来解决局部观测的累计漂移问题，克服GPS数据的不平滑和低频输出。通过将GPS坐标转换为大地坐标并以第一帧GPS为原点，利用最小二乘法进行优化。在代码实现中，对GPS和VIO数据进行处理，转换坐标系，并通过Ceres进行优化。目标是实现局部精确和全局零漂。
VINS_FUSION的global融合思想
使用全局融合的原因
- 局部观测存在累计漂移,室外大场景难以运行
- 局部观测数据缺乏全局约束,导致在不同的位置进行建图和定位都会得到不同坐标系下的结果,难以进行全局结果的观测
GPS的缺点
- 数据不平滑,噪声过大
- 输出频率低(1hz)
融合的目的
- 局部精确
- 全局零漂
算法架构
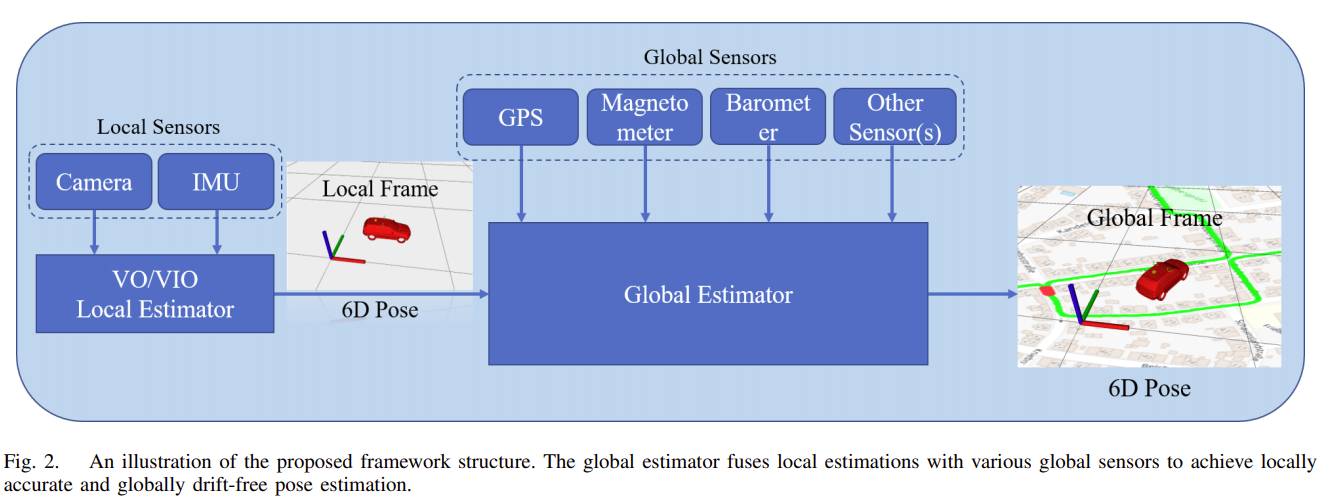
观测和状态约束关系
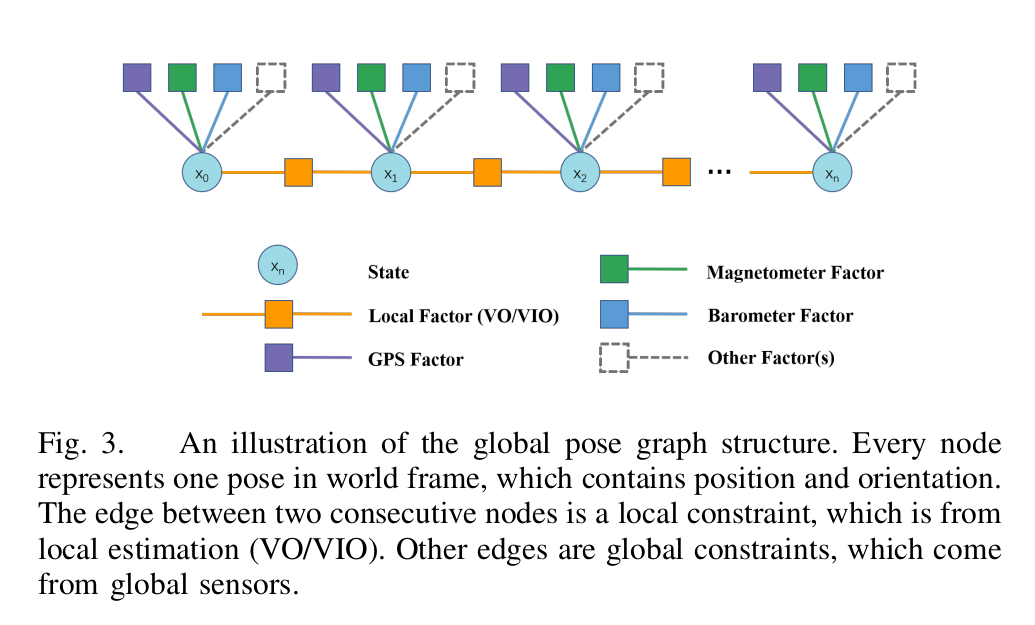
- state: 状态量,位姿,速度,bias等
- Local Factor: 局部观测约束,VIO相对位姿变换, 计算的是相邻两帧之间位姿的残差
GPS 融合思路
- 经纬度坐标系转换为大地坐标系(东北天坐标系ENU:local East North Up)
- 第一帧的gps点为坐标系原点
- 求最小二乘
X ∗ = arg max x ∏ t = 0 n ∏ k ∈ S e x p ( − 1 2 ∥ z t k − h t k ( X ) ) ∥ Ω t k 2 ) = arg min x ∑ t = 0 n ∑ k ∈ S ∥ z t k − h t k ( X ) ) ∥ Ω t k 2 . \begin{aligned}X^* &= \mathop{\arg\max}_{x} \ \ \prod_{t=0}^{n}\prod_{k\in S}exp(-\frac{1}{2} \|z_t^k-h_t^k(X))\|^2_{\Omega_t^k}) \\ &= \mathop{\arg\min}_{x} \ \ \sum_{t=0}^{n}\sum_{k\in S}\|z_t^k -h_t^k(X))\|^2_{\Omega_t^k}. \end{aligned} X∗=argmaxx t=0∏nk∈S∏exp(−21∥ztk−htk(X))∥Ωtk2)=argminx t=0∑nk∈S∑∥ztk−htk(X))∥Ωtk2. - 注意这里的马氏距离要进行一个分解才可以进行最小二乘
∥ r ∥ Ω 2 = r T Ω − 1 r \|r\|^2_Ω = r^T\Omega^{-1}r ∥r∥Ω2=r
最低0.47元/天 解锁文章
扫一扫
769
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
