Codeforces 707D

给一个n行m列的书架，m次操作

1 x y 在x行y列的位置上放置一本书，如果有书在这个位置，跳过

2 x y 在x行y列的位置上拿去一本书，如果没有书在这个位置，跳过

3.x 反转x行的所有位置，即在x行所有没有书的地方放一本书，有书的地方拿走

4.x 回到第x次操作后

前三种操作是容易的，但值得注意的是，第三种操作是需要用懒标记来标记是否有反转过的，两次反转会抵消，所以某个位置的真实情况应该是has[i][j]^tag[i][j]，不用懒标记而是暴力模拟时间复杂度会高。

难点在于4，4是回到之前的某个版本，可以把每次操作抽象成一个点，编号为u点就代表刚刚操作完u，那么如果要回到x操作之后，我们只需要把i操作接到x之后，也就是i与x连边，如果是1-3操作，那么只需与上个操作连边，然后借助dfs回溯的特性，我们如果需要回到x版本，那么在i位置是没有路可走的，会一路回溯到x，此时就可以进行回溯之后的操作了。关于如何回溯，一开始我想的是保存整个局面，但这样空间复杂度是不可行的，我们只需要在回溯之前消除这次操作的影响就可以，因为我们是每个局面分别计算，而局面1+操作=局面2，局面2-操作=局面1，这个思想应该是基础dfs就有了，属于是走弯路了。

需要注意的是，这个算法需要保存所有操作，离线处理，在保存答案的时候，应该是按照点的编号保存，而不是时间顺序，因为在回溯的路径上可能有经过某个点需要多个操作。

关于存边，链式前向星应该是可行的，补题的时候思考错误认为要按照时间顺序，所以改用了vector，但其实不需要关心时间的，关心的是局面状态之间的转移。

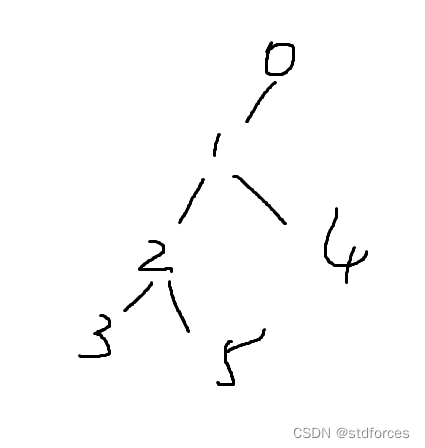
比如到达3后有操作要求回到4，但是我们是按照dfs序来离线操作的，所以获取答案的顺序不一定是时间顺序。

 补题的时候设置了个计数器done，按照时间顺序来编号答案了，一直WA9，看了数据才反应过来。

另外，回溯的时候切记要删去这次操作的影响。

#include<bits/stdc++.h>
#define ll long long
using namespace std;

struct node
{
	int to,x,y,op;
};

vector<node>go[100005];
int n,m,q,done;
bool has[1005][1005],tag[1005];
int sum[1005],tot,ans[100005];

void add(int u,int v,int op,int x,int y)
{
	node add;
	add.to=v;add.op=op;
	add.x=x;add.y=y;
	go[u].push_back(add);
}

void dfs(int u,node todo)
{
	int op=todo.op,x=todo.x,y=todo.y;
	bool suc_to_add=false,suc_to_del=false;//在这次操作中，保存是否成功放置书或者成功拿走书的变量
	if(op==1)
	{
		if(!(has[x][y]^tag[x]))
		{
			sum[x]++;tot++;
			suc_to_add=true;
			has[x][y]=!has[x][y];
		}
	}
	else if(op==2)
	{
		if(has[x][y]^tag[x])
		{
			sum[x]--;tot--;
			suc_to_del=true;
			has[x][y]=!has[x][y];
		}
	}
	else if(op==3)
	{
		tag[x]=!tag[x];
		tot+=m-2*sum[x];
		sum[x]=m-sum[x];
	}
	ans[u]=tot;//此处保存答案要按照编号保存，不是时间顺序
	for(auto i:go[u])
	{
		int v=i.to;
		dfs(v,i);
	}
	if(op==1&&suc_to_add)
	{
		has[x][y]=!has[x][y];
		sum[x]--;tot--;
	}
	else if(op==2&&suc_to_del)
	{
		has[x][y]=!has[x][y];
		sum[x]++;tot++;
	}
	else if(op==3)
	{
		tag[x]=!tag[x];
		tot+=m-2*sum[x];
		sum[x]=m-sum[x];
	}
}

int main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m>>q;
	for(int i=1;i<=q;i++)
	{
		int op,x,y;cin>>op;
		if(op==1||op==2)
		{
			cin>>x>>y;
			add(i-1,i,op,x,y);
		}
		else if(op==3)
		{
			cin>>x;
			add(i-1,i,op,x,y);
		}
		else
		{
			cin>>x;
			add(x,i,op,x,y);
		}
	}
	for(auto i:go[0])
	{
		int v=i.to;
		dfs(v,i);
	}
	for(int i=1;i<=q;i++) printf("%d\n",ans[i]);
 	return 0;
}