5.OpenGL视口变换、裁减、剪切与反馈（笔记）

观察视图

显示器本身是一个平面的、固定的，二维矩形区域，模型却是一个三维空间的几何体。将三维空间的模型投影到二维的关键方法，就是齐次坐标的应用、矩阵乘法的线性变换，以及视口映射。

相机模型

常见的视图变换操作可以类比为使用照相机拍摄照片的过程。

步骤如下：

1. 将相机移动到准备拍摄的位置，将它对准某个方向（视图变换，view transform）。
2. 将准备拍摄的对象移动到场景中必要的位置上（模型变换，model transform）。
3. 设置相机的焦距，或者调整缩放比例（投影变换，projection transform）。
4. 拍摄照片（应用变换结果）。
5. 对结果图像进行拉伸或者挤压，将它变换到需要的图片大小（视口变换，viewport transform）。对于3D图形来说，这里同样需要对深度信息进行拉伸或者挤压（深度范围的缩放）。

第1步和第2步合并为一个模型-视图变换（model-view transform），这一合并过程的主要特性，就是构建一个独立的、统一的空间系统，将场景中所有的物体都变换到视图空间，或者人眼空间（eye space）当中。

下图为OpenGL中的坐标系统，坐标系统均使用左侧的信息来表达，中间的盒子表示从一个坐标变换到另一个的过程，右侧给出了不同过程中的数据单位。

从图中可以看到整个观察矩阵堆栈中包含的所有内容，最后一步就是设置OpenGL的视口和深度范围。OpenGL得到的最终坐标是归一化之后的齐次坐标，并且将进行裁减、剪切和光栅化的操作。也就是说，最后要绘制的坐标在[-1.0，1.0]的范围内，直到OpenGL对它们进行缩放以匹配视口大小。

视椎体

操作相机的第3步，设置焦距或者缩放的数值，这其实就是相机拍摄场景中，设置取景用的矩形椎体的宽度或者窄度。只有落于椎体内的几何体才会出现在最终图像上。同时，还计算用于透视投影的"近大远小"效果的相关参数（齐次坐标的第四个坐标值w）。

OpenGL可以去除过近或者是过远的几何体，因此，需要在增加两个平面，并且与已有的视景椎体的四个平面相交。这6个平面会定义出一个平截椎体（frustum）形状的观察范围。

视椎体的剪切

如果某个图元落在组成视椎体的四个平面之外，那么它将不会被绘制（它将被裁减，cull），因为此时这个图元已经落在矩形的显示区域之外。

如果一个图元正好穿过某个平面，OpenGL将会对此图元进行剪切（clip）,会计算几何体与平面的交集，将落入视椎体范围内的形状进行计算后生成新的几何体。

正交视图模型

有时并不需要透视形式的窗口，而是采用正交（orthographic）投影的方式。这种投影方式常见于建筑设计图和计算机辅助设计的领域，主要作用是在投影之后依然保持物体的真实大小以及相互之间的角度。

可以简单地通过忽略x、y、z三个坐标轴中的一个来实现这一效果，也就是其余两个构成二维坐标。

用户变换

以上所述的视图模型的每个步骤都可以通过一次控件变换来表达，它们全部都是线性变换方式，可以通过齐次坐标的矩阵乘法来完成。

齐次坐标

进行变换的几何体本身就是三维形式，将三维的笛卡尔坐标转换为四维的齐次坐标，有两个优点：其一，可以进一步完成透视变换；其二，这样可以使用线性变换来实现模型的平移，使用了四维坐标系统，就可以通过矩阵乘法完成所有的旋转、平移、缩放和投影变换操作。

齐次坐标总是有一个额外的分量，并且如果所有的分量都除以一个相同的值，那么将不会改变它所表达的坐标位置。

举例来说，以下所有的坐标都表达了同一个点：
$$\begin{gathered} (2.0,3.0,5.0,1.0) \\ (4.0,6.0,10.0,2.0) \\ (0.2,0.3,0.5,0.1) \end{gathered}$$
一般直接添加第四个w分量，并设置值为1.0来实现齐次坐标的建立；使用第四个分量除以所有的分量，并且将其舍弃，以重新获得笛卡尔坐标。

当OpenGL准备显示几何体的时候，它会使用最后一个分量除以前三个分量，从而获得齐次坐标重新变换到三维的笛卡尔坐标。因此距离更远的物体（w值更大）的笛卡尔坐标也会更小，从而绘制的比例也会更小。

ω的零值和负值会带来较差的效果，因此要保证w值总是正数。

线性变换与矩阵

为了将数据映射到设备坐标系当中，首先对三维的笛卡尔坐标添加第四个分量，并且设置值为1.0，从而构建了齐次坐标。这些坐标通过与一个或多个4x4矩阵的乘法运算来表达旋转、缩放、平移以及透视投影的变换过程。

平移

例如，沿x轴正方向平移2.5
$$\left(\begin{array}{c}x+2.5\\ y\\ z\\ 1.0\end{array}\right)=\left(\begin{array}{cccc}1.0& 0.0& 0.0& 2.5\\ 0.0& 1.0& 0.0& 0.0\\ 0.0& 0.0& 1.0& 0.0\\ 0.0& 0.0& 0.0& 1.0\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1.0\end{array}\right)$$

如果要使用工具库构建一个平移矩阵，可以调用：

vmath::mat4 vmath::translate(float x,float y,float z);

返回一个平移矩阵，平移距离为（x，y，z）。

示例：

#include "vmath.h"

//构建一个变换矩阵，将坐标平移（1,2,3）
vmath::mat4 translationMatrix = vmath::translate(1.0,2.0,3.0);
//将这个矩阵传递给当前的着色器程序
glUniformMatrix4fv(matrix_loc,1,GL_FALSE,translationMatrix);

缩放

例如，将几何体放大原来大小的3倍
$$\left(\begin{array}{c}3x\\ 3y\\ 3z\\ 1.0\end{array}\right)=\left(\begin{array}{cccc}3.0& 0.0& 0.0& 0.0\\ 0.0& 3.0& 0.0& 0.0\\ 0.0& 0.0& 3.0& 0.0\\ 0.0& 0.0& 0.0& 1.0\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1.0\end{array}\right)$$

注意，因为缩放值是针对每个分量的，所以很容易做到非同型的缩放变换，但是在设置模型和视图变换的时候很少这么做。这是因为，如果需要将结果进行垂直或水平的拉伸，可以在视图变换完成之后进行。过早进行缩放会导致物体在旋转的时候变形。

注意，进行缩放时，并不会影响w值，否则会由于齐次坐标本身的特性（最后所有的分量都会除以w），结果不会发生改变。

如果物体缩放时，其中心没有处于(0，0，0)点，那么矩阵在缩放的同时也会将物体远离或者靠近(0，0，0)。如果需要改变一个偏移中心的物体大小，并且不希望它的位置同时发生改变，那么我们可以将物体中心移动到(0，0，0)，然后再缩放大小，最后平移回到原来的位置。
$$\begin{gathered} M=T^{-1}ST \\ {v}^{\prime }=Mv \end{gathered}$$
使用工具库完成缩放，可以使用函数：

vmath::mat4 vmath::scale(float s);

返回一个缩放倍数为s的变换矩阵。

示例：

//C++ 程序代码
#include "vmath.h"

// 将平移和缩放变换进行合并
vmath::mat4 translateMatrix = vmath::translate(1.0,2.0,3.0);
vmath::mat4 scaleMatrix = vmath::scale(5.0);
vmath::mat4 scaleTranslateMatrix = scaleMatrix * translateMatrix;

旋转

• 绕Z轴旋转
  $$R_z=\left(\begin{array}{cccc}cos\theta & -sin\theta & 0.0& 0.0\\ sin\theta & cos\theta & 0.0& 0.0\\ 0.0& 0.0& 1.0& 0.0\\ 0.0& 0.0& 0.0& 1.0\end{array}\right)$$

  $$\left(\begin{array}{c}cos\theta \times x-sin\theta \times y\\ sin\theta \times x+cos\theta \times y\\ z\\ 1.0\end{array}\right)=\left(\begin{array}{cccc}cos\theta & -sin\theta & 0.0& 0.0\\ sin\theta & cos\theta & 0.0& 0.0\\ 0.0& 0.0& 1.0& 0.0\\ 0.0& 0.0& 0.0& 1.0\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1.0\end{array}\right)$$

• 绕X轴旋转
  $$R_x=\left(\begin{array}{cccc}1.0& 0.0& 0.0& 0.0\\ 0.0& cos\theta & -sin\theta & 0.0\\ 0.0& sin\theta & cos\theta & 0.0\\ 0.0& 0.0& 0.0& 1.0\end{array}\right)$$

• 绕Y轴旋转
  $$R_y=\left(\begin{array}{cccc}cos\theta & 0.0& -sin\theta & 0.0\\ 0.0& 1.0& 0.0& 0.0\\ sin\theta & 0.0& cos\theta & 0.0\\ 0.0& 0.0& 0.0& 1.0\end{array}\right)$$

旋转都是沿着第一个轴的方向朝向第二个轴运动的，也就是说，按照各轴的正向顺序，从cos-sin形式的一行旋转到sin + cos的一行。如果被旋转的物体中心不是（0,0,0），那么上面的矩阵也会绕（0,0,0）将物体整体进行转动，因而改变位置。

因此整个过程，可以是先平移到（0,0,0），再执行旋转变换，然后再平移回到原位。

使用工具构建旋转矩阵，可以使用函数：

vmath::mat4 vmath::rotate(float x,float y,float z);

返回一个变换矩阵，它可以绕x轴转动x度、绕y轴转动y度、以及绕z轴转动z度。

可以直接将这个矩阵（左乘）级联到当前矩阵之上。

透视投影

考虑以下两种情形：

1. 中心对称的视图截锥，z轴位于椎体的中央位置
2. 不对称的视图截锥，就好像我们靠近窗口，观察景色，但是没有正对窗户中心的情形。

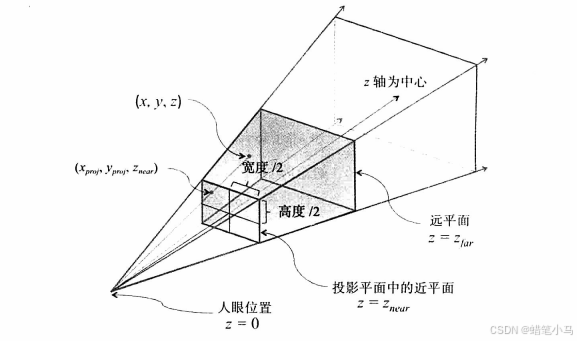
• 中心对称的视图截锥
  $$\left(\begin{array}{cccc}\frac{Z_{near}}{width/2}& 0.0& 0.0& 0.0\\ 0.0& \frac{Z_{near}}{height/2}& 0.0& 0.0\\ 0.0& 0.0& -\frac{Z_{far}+Z_{near}}{Z_{far}-Z_{near}}& \frac{2Z_{far}{Z}_{near}}{Z_{far}-Z_{near}}\\ 0.0& 0.0& -1.0& 0.0\end{array}\right)$$

• 不对称的视图截锥
  $$\left(\begin{array}{cccc}\frac{Z_{near}}{width/2}& 0.0& \frac{left+right}{width/2}& 0.0\\ 0.0& \frac{Z_{near}}{height/2}& \frac{top+bottom}{height/2}& 0.0\\ 0.0& 0.0& -\frac{Z_{far}+Z_{near}}{Z_{far}-Z_{near}}& \frac{2Z_{far}{Z}_{near}}{Z_{far}-Z_{near}}\\ 0.0& 0.0& -1.0& 0.0\end{array}\right)$$

使用工具库，创建一个透视投影的变换矩阵，可以使用frustum函数。

vmath::mat4 vmath::frustum(float left,float right,float bottom,float top,float near,float far);

根据给定的视椎体设置返回一个透视投影矩阵。近平面矩形通过left、right、bottom和top定义。近平面和远平面的距离通过near和far定义。

正交矩阵

正交投影得到的观察体形状是一个矩形的平面六面体，或者更通俗的说，是一个盒子。与透视矩阵不同，这个观察体远近两端的尺寸不会发生变化，因此物体与相机的距离不会造成物体大小的变化。

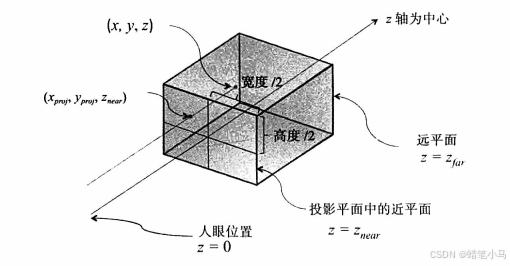
正交投影，从平行六面体的正面直接进行投影。x、y、z都需要经过缩放以分别符合[-1,1]、[-1,1]和[0,1]的范围要求。这一过程可以通过顶点除以模型的宽度、高度、和深度来完成。

• z轴正方向中心位置 穿过 中心对称的观察体
  $$\left(\begin{array}{cccc}\frac{1}{width/2}& 0.0& 0.0& 0.0\\ 0.0& \frac{1}{height/2}& 0.0& 0.0\\ 0.0& 0.0& -\frac{1}{(Z_{far}-Z_{near})/2}& -\frac{Z_{far}+Z_{near}}{Z_{far}-Z_{near}}\\ 0.0& 0.0& -1.0& 0.0\end{array}\right)$$

• z轴正方向 没有穿过观察体中心（但平行于z轴观察模型）
  $$\left(\begin{array}{cccc}\frac{1}{(right-left)/2}& 0.0& 0.0& -\frac{right+left}{right-left}\\ 0.0& \frac{1}{(top-bottom)/2}& 0.0& -\frac{top+bottom}{top-bottom}\\ 0.0& 0.0& -\frac{1}{(Z_{far}-Z_{near})/2}& -\frac{Z_{far}+Z_{near}}{Z_{far}-Z_{near}}\\ 0.0& 0.0& -1.0& 0.0\end{array}\right)$$

使用工具库创建正交投影变换矩阵，可以使用如下函数：

vmath::mat4 vmath::ortho(float left,float right,float bottom,float top,float near,float far);

返回一个正交投影矩阵。近平面矩形通过left、right、bottom和top定义。近平面和远平面的距离通过near和far定义。

法线变换

法线，是从某点出发，方向与物体表面垂直的一个向量。出于光照计算的目的，法线需要进行归一化。

法线向量通常是只有三个分量的向量，没有使用齐次坐标。

• 一个原因是，物体表面的平移不会影响到法线的值，因此法线不用考虑平移
• 另一个原因，法线的主要作用是光照计算，而这一步通常在透视变换前完成，因此不需要使用齐次方程处理投影变换。

法线向量的变换与顶点或位置向量的变换不同，假设一个3×3矩阵为M，其中包含了旋转和缩放变换信息，可以将物体从模型坐标系变换到眼坐标系，但不包含透视变换信息。依据此矩阵，可使用如下方程完成法线变换：
$$n^{\prime }=M^{-1T}n$$
也就是说使用M的逆矩阵的转置完成法线变换。

OpenGL变换

近平面和远平面的设置

void glDepthRange(GLdouble near,GLdouble far);
void glDepthRangef(GLdouble near,GLdouble far);

设置z轴上的近平面位于near，而远平面位于far。这个函数定义了视口变换过程中z坐标的变换范围。近平面和远平面的值也就是深度缓存中所保存的最小值和最大值。默认情况下它们分别是0.0和1.0，这对于大部分应用程序都是适用的。这个函数的参数设置范围必须是[0,1]之间的数值。

• 视口

  指定显示数据的矩形观察区

  void glViewport(GLint x,GLint y,GLint width,GLint heigt);
  

  在程序窗口中定义一个矩形的像素区域，并且将最终渲染的图像映射到其中。这里x和y参数设置了视口（viewport）的左下角坐标，而width和height设置了视口矩形的像素大小。默认情况下视口初始值设置为（0,0,winWidth,winHeight）,其中winWidth和winHeight为窗口的像素尺寸。

  平台的窗口操作系统，而非OpenGL本身，将负责在屏幕上打开一个窗口。默认情况下，视口设置为打开窗口的整个像素区域。可以使用glViewport()来选择一个更小的绘制区域；例如，可以通过分割窗口来模拟同一个窗口中多个视图分裂的效果。

• 多视口

  有时候需要使用多个视口来完成一个场景的渲染。OpenGL提供了相应的命令支持，并且可以在几何着色阶段选择具体要进行绘制的视口。

• 高级技巧：z的精度

  上述变换可能会产生一个不太理想的效果，就是z-fighting。计算过程中，硬件的浮点数精度支持是有限的。因此有的时候虽然在数学上深度坐标应该是不同的，但是硬件上最终记录的浮点数z值可能是相同（甚至与实际结果相反）。

  这样会造成深度缓存中的隐藏面中计算结果不正确。由于这个现象可能对多个像素都有影响，因而导致相互距离较为接近的物体会发生闪烁交叠的情形。经过透视变换之后，z的精度问题可能会恶化，无论对于深度坐标还是其他类型的坐标值都是如此：此时如果深度坐标远离近剪切平面，那么它的位置精度将越来越低。

  就算没有经过透视变换，浮点数的精度也是有限的，而透视的结果会导致它恶化并且成为非线性的形式，在深度值较大时会带来更多的问题。

  问题的根源：是我们在一个过小的z值区域绘制了过多的数据。如果要避免这个问题，需要尽量将远平面与近平面靠近，并且尽可能不要在很小的区域内绘制过多的z值。

高级技巧：用户裁剪与剪切

OpenGL会自动根据视口和近平面与远平面的设置来裁减和剪切几何体。用户裁减和剪切的意思就是再添加一些任意方向的平面，与几何数据相交，例如只允许几何体在平面的一侧可见，而另一侧不可见。

OpenGL的用户裁减和剪切操作需要特殊的内置顶点着色器数组gl_CullDistance[]和gl_ClipDistance[]联合产生作用，这两个变量允许我们控制裁减和剪切平面与顶点的关系。它们的值经过插值之后设置给顶点之间的各个片元。

#version 450 core

uniform vec4 Plane;			//平面方程Ax+By+Cz+D=0的四个系数
in vec4 Vertex;				//w == 1.0
float gl_ClipDistance[1];	//使用一个剪切平面

void main()
{
    //计算平面方程
    gl_ClipDistance[0] = dot(Vertex,Plane);
    //也可以使用gl_CullDistance[0]来进行裁减
}

这个变量的含义是，距离为0表示顶点落在平面之上，正数值表示顶点在剪切平面的内侧（保留这个顶点），负数值表示顶点在剪切平面的外侧（裁减这个顶点）。在图元中剪切距离是线性插值的。OpenGL会负责将完全落在某个裁减平面之外的图元剔除。如果图元与所有的裁减平面相交且有一部分落在它们的内侧，则认为它应当被保留。

gl_ClipDistance和gl_CullDistance数组的每个元素都对应于一个平面。平面的数量是有限的，通常为8个或者更多，并且通常这个数量是gl_ClipDistance和gl_CullDistance数组共享的。

也就是说，你可以分配8个剪切平面，或者分配8个裁减平面，或者各分配4个，或者按照2个和6个来划分，但是这两个数组的平面总数不能超过8个。这个总数的距离值可以通过gl_MaxCombinedClipAndCullDistance来查询，此外针对裁减平面的最大值是gl_MaxCullDistances，针对剪切平面的最大值是gl_MaxClipDistances。

注意，内置的gl_ClipDistance[]变量在声明时并没有指定大小，而我们用到的平面数量（数组元素）是在着色器中设置的。因此需要重新声明它的大小，或则将它作为一个编译时的常量使用。这里的大小表示我们将会使用的平面数量。

所有声明或者使用了gl_ClipDistance[]与gl_CullDistance[]的着色器都必须将数组设置为同样的大小。这个数组内必须包含所有已经通过OpenGL API启用的剪切平面；如果它没有包括所有启用的剪切平面，那么得到的结果可能是不确定的。

启用剪切平面：

glEnable(GL_CLIP_PLANE0);

其他可用的枚举量还有GL_CLIP_PLANE1、GL_CLIP_PLANE2等。这些枚举量是按顺序定义的，因此GL_CLIP_PLANEi总是等价于GL_CLIP_PLANE0+i。着色器中必须写入所有启用的平面距离值，否则可能会得到奇怪的剪切结果。

在片元着色器中内置变量gl_CullDistance和gl_ClipDistance也是可用的，没有被剪切的片元可以读取每个剪切平面的距离插值结果。

OpenGL变换的控制

很多OpenGL的固定流水线函数操作都是在剪切空间发生的，也就是顶点着色器（或者细分和几何着色器，如果开启了的话）生成的坐标。默认情况下，OpenGL会映射剪切空间的坐标（0,0）到窗口空间的中心，x坐标轴正向指向右侧，y坐标轴正向指向上方。

考虑到连续性与正交性的需求，可见的x和y的取值范围是从-1.0到1.0，因此可见的深度取值范围也应该是-1.0到1.0，这里的-1.0表示近平面的所在的位置，1.0表示远平面的位置。

但是必须说明的是，由于浮点数本身的工作机制，精度比较高的区域主要集中在0.0附近，而这个区域距离观察者可能是比较远的，但是我们期望的实际上是靠近观察者（近平面）的区域能够有更高的深度精度。当然，其他一些图形系统会使用另一种映射方式，剪切空间中-z的坐标值表示观察者身后的位置，因此可见的深度范围在剪切空间中会被映射到0.0到1.0。

OpenGL可以配置这两种映射方式：

void glClipControl(GLenum origin,GLenum depth);

设置剪切坐标到窗口坐标的映射方式。origin设置的是窗口坐标x和y的原点，而depth设置的是剪切空间深度值映射到glDepthRange()所设置的数值方式。

origin必须是GL_LOWER_LEFT或者GL_UPPER_LEFT中的一个。如果origin是GL_LOWER_LEFT，那么剪切空间的xy坐标（-1.0,-1.0）对应的窗口坐标的左下角，剪切空间中的y轴正向对应窗口空间中的上方向。如果origin是GL_UPPER_LEFT，那么剪切空间的xy坐标（-1.0,-1.0）对应窗口坐标的左上角，剪切空间中的y轴正向对应窗口空间的下方向。

如果depth设置为GL_NEGATIVE_ONE_TO_ONE，那么窗口空间中的深度对应于剪切空间的[-1.0,1.0]的范围。如果depth设置为GL_ZERO_TO_ONE，那么剪切空间的[0.0,1.0]范围被映射到窗口空间的深度值，此时0.0表示近平面，1.0表示远平面。剪切空间的z负值变换后将处于近平面的后方，但是观察着眼前的数据精度会变得更高。

tranform feedback

transform feedback是OpenGL管线中，顶点处理阶段结束之后，图元装配和光栅化之前的一个步骤。transform feedback可以重新捕获即将装配为图元（点、线段、三角形）的顶点，然后将它们的部分或者全部属性传递到缓存对象中。

transform feedback对象

transform feedback状态是封装在一个transform feedback对象中的。这个状态中包括所有用于记录顶点数据的缓存对象、用于表示缓存对象的充满程度的计数器，以及用于标识transform feedback当前是否启用的状态量。

transform feedback对象的创建需要一个对象名称，然后将它绑定到当前环境的transform feedback对象绑定点上。如果要分配一个transform feedback对象的名称，则可以使用：

void glCreateTransformFeedbacks(GLsizei n,GLuint* ids);

创建n个新的transform feedback对象，并且将生成的名称记录到数据ids中。

当我们创建了一个transform feedback对象之后，它会包含一个默认的transform feedback状态，并在需要的时候绑定到环境。对象绑定到当前环境函数如下：

void glBindTransformFeedback(GLenum target,GLuint id);

将一个名称为id的transform feedback对象绑定到目标target上，目标的值必须是GL_TRANSFORM_FEEDBACK

如果判断某个值是否是一个transform feedback对象的名称，可以调用如下函数：

GLboolean glIsTransformFeedback(GLuint id);

如果id是一个已有的transform feedback对象的名称，那么返回GL_TRUE，否则返回GL_FALSE。

系统内置了一个默认的对象，这个默认的transform feedback对象的id为0，因此如果给glBindTransformFeedback()的id参数传递，则相当于重新回到默认的transform feedback对象上，解除所有之前绑定的transform feedback对象。

如果不在需要某个transform feedback对象，可以通过下面的命令删除它：

void glDeleteTransformFeedbacks(GLsizei n,const GLuint* ids);

删除n个transform feedback对象，其名称保存在数组ids中。如果ids的某个元素不是transform feedback对象的名称，或者设置为0，那么都会被直接忽略，不会给出提示。

删除对象的操作会延迟到所有相关的操作结束之后才进行，也就是说，如果当前transform feedback对象处于启用状态，而我们调用glDeleteTransformFeedbacks()，那么只有本次transform feedback结束之后，才会删除对象。

transform feedback 缓存

transform feedback对象主要用于管理将顶点捕捉到缓存对象的相关状态。这个状态中包含当前连接到transform feedback缓存绑定点的缓存对象。

我们可以同时给transform feedback绑定多个缓存，也可以绑定缓存对象的多个子块。甚至可以将同一个缓存对象的不同子块同时绑定到不同的tramsform feedback缓存绑定点。

将整个缓存对象绑定到某个transform feedback缓存绑定点上，可以用如下函数：

void glTransformFeedbackBufferBase(GLuint xfb,GLuint index,GLuint buffer);

将名为buffer的缓存对象绑定到名为xfb的transform feedback对象上，其索引通过index设置。如果xfb为0，那么buffer将绑定到默认的transform feedback对象的绑定点。

xfb对象，可以有多个绑定点（索引），每个绑定点可以关联不同的缓存区对象。

由于transform feedback对象都是独立的，因此不同的变换反馈对象即使使用相同的绑定点，也不会相互影响。它们各自处理自己的数据，并将结果存储在自己的绑定的缓冲区对象中。

这里的index必须是当前绑定的transform feedback对象的缓存绑定点索引。绑定点总数是一个与具体设备实现相关的常量，可以通过GL_MAX_TRANSFORM_FEEDBACK_BUFFERS的值来查询，而index必须小于这个值。所有的OpenGL设备实现都可以支持至少64个transform feedback缓存绑定点。

也可以将一个缓存对象的一部分绑定到某个transform feedback缓存绑定点，相关函数为：

void glTransformFeedbackBufferRange(GLuint xfb,GLuint index,GLuint buffer,GLintptr offset,GLsizeiptr size);

将缓存对象buffer的一部分绑定到名为xfb的transform feedback对象的绑定点索引index上。offset和size的单位均为字节，它们设置了要绑定的缓存对象的范围。如果xfd为0，那么buffer将绑定到默认的transform feedback对象的绑定点。

这个函数可以用来将同一个缓存对象的不同区域绑定到不同的transform feedback绑定点。保证这些区域是互不交叠的。我们需要保证这些区域是互不交叠的。如果对同一个缓存对象的多个互相重叠区域应用transform feedback，那么得到的结果将是不确定的，有可能造成数据的错误，或者更糟的情况。

//创建新的缓存对象
GLuint buffer;
glCreateBuffers(1,&buffer);

//调用glNamedBufferStorage并分配
glNamedBufferStorage(buffer,		//缓存
                     1024*1024,		//1MB空间
                     NULL,			//无初始数据
                     0);			//标志量

//Now we can bind it to indexed buffer bingding points
glTransformFeedbackBufferRange(xfb,			//对象
                               0,			//索引0
                               buffer,		//缓存名称
                               0,			//数据范围的起始地址
                               512*1024);	//缓存的前半部分

glTransformFeedbackBufferRange(xfb,			//对象
                              1,			//索引1
                              buffer,		//同一个缓存
                              512*1024,		//数据范围的起始地址
                              512*1024);	//缓存的后半部分

在上述例子中，我们调用了两次glTransformFeedbackBufferRange()，不过OpenGL还提供了另一个快捷的函数，帮助用户绑定到大量不同的范围或者大量不同的缓存。它可以用来绑定一系列范围相同或者不同的缓存到同一个目标的多个不同的索引点。原型为：

void glBindBuffersRange(GLenum target,GLuint first,GLsizei count,const GLuint *buffers,const GLintptr *offsets,const GLsizeiptr *sizes);

绑定来自一个或者多个缓存的多个范围值，对应于target所指定的目标绑定点。first表示绑定缓存范围的第一个索引值，count表示要绑定的数量。

这里的buffers、offsets、sizes参数分别对应于数组中的count个缓存名称，count个起始地址偏移量，count个绑定范围的大小。offsets和sizes中保存的数值是采用字节方式设置的。这里的每一个范围数据都是通过offsets和sizes中的对应元素指定的，然后绑定到target所指定的索引位置，从first开始计数。

如果buffers为NULL，那么offsets和sizes将被忽略，同时target的索引绑定点上所有的绑定关系会被删除。

配置transform feedback的变量

transform feedback所绑定的缓存是与一个transform feedback对象关联在一起的，顶点(或者几何)着色器的输出要记录在那些缓存当中，这些配置信息是保存在当前程序对象当中的。

有两种方式设置transform feedback过程中要记录的变量：

• 通过OpenGL API：glTransformFeedbackVarings()。
• 通过着色器：xfb_buffer、xfb_offset和xfb_stride。

同时只能使用一种方法来配置。

通过OpenGL API配置transform feedback变量

void glTransformFeedbackVaryings(GLuint program,GLsizei count,const GLchar** varings,GLenum bufferMode);

设置使用varyings来记录transform feedback的信息，所用的程序通过program来指定。count设置varyings数组中所包含的字符串数量，它们存储的也是所有要捕获的变量名称。bufferMode设置的是捕获变量的模式——可以是分离模式（GL_SEPARATE_ATTRIBS）或者交叉模式（GL_INTERLEAVED_ATTRIBS）。

如果bufferMode设置为GL_INTERLEAVED_ATTRIBS，那么所有的变量是一个接着一个记录在绑定到当前transform feedback对象的第一个绑定点的缓存对象里的。如果bufferMode为GL_SEPARATE_ATTRIBS，那么每个变量都会记录到一个单独的缓存对象中。

//创建一个包含准备记录变量名称的数组
static const char* const vars[] = 
{
    "foo","bar","baz"
};
//调用 glTransformFeedbackVarings 函数
glTransformFeedbackVarings(prog,
                           sizeof(vars)/sizeof(vars[0]),
                           varings,
                           GL_INTERLEAVED_ATTRIBS);
//上述函数，将同一个缓存对象中连续记录多个变量
glTransformFeedbackVarings(prog,
                          sizeof(vars)/sizeof(vars[0]),
                          varings,
                          GL_SEPARATE_ATTRIBS);
//上述函数，可以将变量记录到分离的缓存当中
//接下来需要链接程序对象，即使之前已经链接过
glLinkProgram(prog);

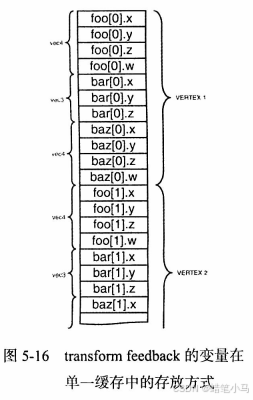
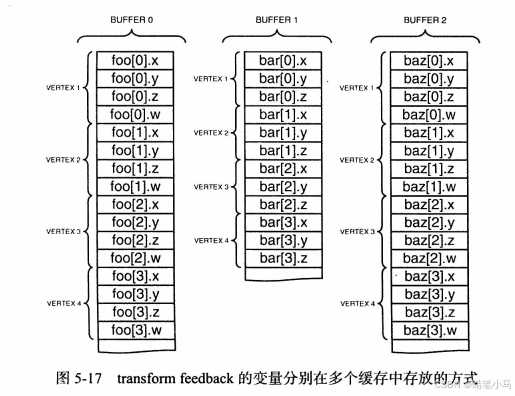
在调用glTransformFeedbackVaryings()之后直接调用glLinkProgram()。这是因为我们在glTransformFeedbackVaryings()中所选择的变量只有程序对象再一次被链接的时候才会起作用。如果程序之前已经经过了链接，而这一次重新进行链接的话，那么不会产生错误，但是transform feedback的过程中也不会返回结果。

在上述两种情况下，属性都是紧密排列着保存的。缓存对象中每个变量所占据的空间总量是由它在顶点着色器中的类型所决定的。不过有时候也需要将写入到transform feedback缓存的数据使用不同的方式进行对齐。

为了增加transform feedback变量设置的灵活性，并且实现这样的工作方式，需要引入一些特殊的OpenGL变量名称，用于标识transform feedback的输出缓存中是否需要流出空隙，或者在缓存中进行移动。相关的内置变量包括gl_SkipComponents1、gl_SkipComponents2、gl_SkipComponents3、gl_SkipComponents4和gl_NextBuffer。

如果OpenGL遇到任何一个gl_SkipComponents变量，就会在transform feedback缓存中留出一个指定数量（1、2、3、4）的空隙。只有bufferMode设置为GL_INTERLEAVED_ATTRIBS时，才可以使用这些变量。

示例1：

//声明 transform feedback的变量名称
static const char* const vars[] = 
{
	"foo",
    "gl_SkipComponents2",
    "bar",
    "gl_SkipComponents3",
    "baz"
};

//设置各个变量
glTransformFeedbackVaryings(prog,
                            sizeof(vars)/sizeof(var[0]),
                            varyings,
                            GL_INTERLEAVED_ATTRIBS);
//不要忘记重新链接程序
glLinkProgram(prog);

如果OpenGL遇到另一个内置变量gl_NextBuffer，那么它会将变量传递到当前绑定的下一个transform feedback缓存中。如果bufferMode为GL_SEPARATE_ATTRIBS时遇到gl_NextBuffer，或者在GL_INTERLEAVED_ATTRIBS模式下一行中遇到两个或多个gl_NextBuffer，那么它将会直接跳过当前的绑定点，并且在当前绑定的缓存中不会记录任何数据。

示例2：

//声明transform feedback的变量名称
static const char* const vars[] = 
{
    "foo","bar",				//记录到缓存0当中的变量
    "gl_NextBuffer",			//移动到绑定点1
    "baz"						//记录到缓存1当中的变量
};
//设置各个变量
glTransformFeedbackVarying(prog,
                           sizeof(vars)/sizeof(vars[0]),
                           varyings,
                           GL_INTERLEAVED_ATTRIBS);
//不要忘记重新链接程序
glLinkProgram(prog);

通过着色器配置transform feedback的变量

在着色器中使用transform feedback变量，我们需要使用以下着色器layout限定符：

• xfb_buffer设置变量对应的缓存。
• xfb_offset设置变量在缓存中的位置。
• xfb_stride设置数据从一个顶点到下一个的排列方式。

//针对一个缓存条件
//一个缓存中的不同变量位置布局
layout(xfb_offset=0) out vec4 foo;			//默认 xfb_buffer为0
layout(xfb_offset=16) out vec3 bar;
layout(xfb_offset=28) out vec4 barz;

//也可以在块中完成同样的操作
layout(xfb_offset=0) out{			//表示偏移地址对应所有变量
    vec4 foo;
    vec3 bar;			//下一个有效的偏移地址
    vec4 barz;
}captured;

//针对多个缓存条件
layout(xfb_buffer=0,xfb_offset=0) out vec4 foo;			//必须有xfb_offset
layout(xfb_buffer=1,xfb_offset=0) out vec3 bar;
layout(xfb_buffer=2,xfb_offser=0) out vec4 barz;

顶点之间的数据对齐可以直接通过xfb_stride来声明缓存中的数据跨幅来完成。在顶点数据块中创建"洞"（忽略某些数据）的方法，则是直接每个要捕捉的变量的精确偏移值。

//多个缓存中的布局（有洞）
layout(xfb_buffer=0,xfb_stride=40,xfb_offset=0) out vec4 foo;
layout(xfb_buffer=0,xfb_stride=40,xfb_offset=20) out vec3 bar;
layout(xfb_buffer=1,xfb_stride=40,xfb_offset=16) out vec4 barz;

layout(xfb_buffer=2,xfb_stride=44) out{
    layout(xfb_offset=0) vec4 iron;
    layout(xfb_offset=28) vec4 copper;
    vec4 zinc;			//没有 xfb_offset,不做捕获
};

跨幅和偏移量的设置值必须是4的倍数，除非其中包含了双精度（double）类型的数据，此时必须设置为8的倍数。当然，一个缓存中可以只有一个跨幅设置，此时该缓存对应的所有的xfb_stride都需要是一致的。

例如：

layout(xfb_buffer=1,xfb_stride=40) out;

之后对这个缓存的数据再使用xfb_offset的时候，会直接采用之前的默认跨幅值。

transform feedback 的启动和停止

transform feedback可以随时启动或者停止，甚至暂停。如果启动transform feedback时，没有处于暂停的状态，则重新开始将数据记录到当前绑定的transform feedback缓存中；若处于暂停状态，那么再次启动将会从暂停的位置开始记录。

void glBeginTransformFeedback(GLenum primitiveMode);

设置transform feedback准备记录的图元类型。primitiveMode必须是GL_POINTS、GL_LINES或者GL_TRIANGLES。在这之后的绘制命令中的图元类型必须与这里的primitiveMode相符，或者几何着色器（如果存在的话）的输出类型必须与primitiveMode相符。

glBeginTransformFeedback()函数从当前绑定的transform feedback对象开始执行。注意，如果用到了细分着色器或者几何着色器，那么绘制命令的图元类型不一定与这里的参数相符，因为这些阶段会再次改变图元类型。目前，我们只需保证primitiveMode与准备绘制的图元类型相符即可。

transform feedback阶段可用的绘制模式
transform feedback的primitiveMode	允许的绘制类型
GL_POINTS	GL_POINTS
GL_LINES	GL_LINES、GL_LINE_STRIP、GL_LINE_LOOP、GL_LINES_ADJACENCY、GL_LINE_STRIP_ADJACENCY
GL_TRIANGLES	GL_TRIANGLES、GL_TRIANGLE_STRIP、GL_TRIANGLE_FAN、GL_TRIANGLES_ADJACENCY、GL_TRIANGLE_STRIP_ADJACENCY

有关transform feedback启用之后再暂停模式下的状态变化，还有其他一些限制条件如下：

• 当前绑定的transform feedback对象不可改变。
• 不允许将其他的缓存绑定到GL_TRANSFORM_FEEDBACK_BUFFER的绑定点
• 当前的程序对象不可改变。

void glPauseTransformFeedback(void);

暂停transform feedback对变量的记录。我们可以通过glResumeTransformFeedback()重新启动transform feedback。

若当前的transform feedback没有启用，或者已经处于暂停状态，glPauseTransformFeedback()将产生一个错误。

void glResumeTransformFeedback(void);

重新启用一个之前通过glPauseTransformFeedback()暂停的transform feedback过程。

如果transform feedback没有启用或者已经启用但是没有处于暂停状态，glResumeTransform都会产生一个错误。

void glEndTransformFeedback(void);

完成transform feedback模式下的变量记录过程。