对抗搜索 学习笔记

先来看一道有意思题

situation

大意：

两个人玩井字棋，要求把所有位置填满后结束游戏。一方希望两者的连起来的线之差最多，一方希望最少。现在给定初始局面（已经存在一些棋子）以及先手，求最后的两者的连起来的线之差。

这就是一道对抗搜索的题目

什么是对抗搜索？简单来说，博弈双方对竞争相反的利益，一方使其最大化，一方使其最小化，那么我们就可以通过搜索来探索最终状态

min-max对抗搜索

假设我们已经有了一颗博弈树：
 

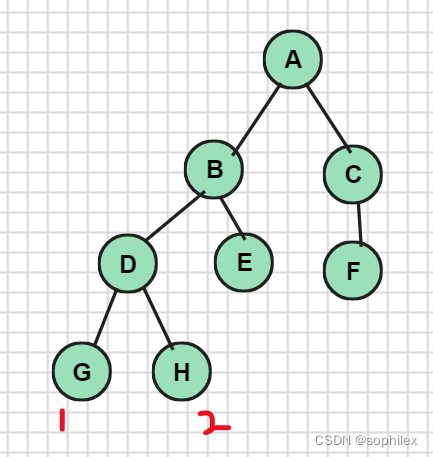
 如果我方先手且我方以最大化利益为目标，那么单数层就是我方的决策层，双数层就是对方的。那么在单数层的节点，它会选取利益最大化的子局面，反之亦然。

现在我们从最底层开始向上，D在单数层，它会选取最大的利益，所以它的利益为2。B就会在D和E的利益之间选取最小的...依次类推，最后我们就可以得到初始局面对应的利益了。

但是当博弈规模比较大的时候，搜索规模也会爆炸，就要考虑剪枝。

这里引入：

Alpha_Beta对抗搜索

我们限定一个利益区间【a,b】

α Alpha is the maximum lower bound of possible solutions 

对于一个追求max利益的节点P，它的所有子节点都是追求min利益，会将收益尽可能降低，那么P就会在所有尽可能低的收益里选最高的，也就是α了。

β Beta is the minimum upper bound