本文探讨了在零和游戏环境下的人工智能对抗搜索，通过Tic-Tac-Toe游戏举例说明minimax算法和alpha-beta pruning优化策略。minimax算法用于最大化智能体的收益，但当游戏树巨大时效率低下。alpha-beta pruning通过剪枝减少搜索节点，提高搜索效率，理想情况下时间复杂度为O(b^m/2)。
二、对抗搜索（Adversarial Search）(博弈搜索 Game Search)
所谓对抗搜索，即在一个竞争环境中，智能体（agents）之间通过竞争实现相反的利益，一方最大化这个利益，另一方最小化这个利益。
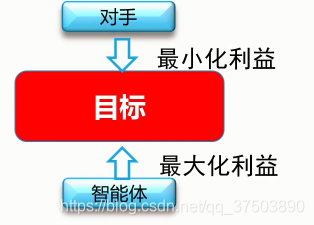
本文主要讨论在确定的、全局可观察的、竞争对手轮流行动、零和游戏（zero-sum）下的对抗搜索。
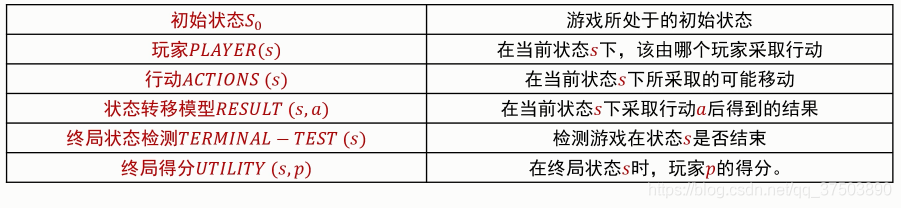
例如，两人对决游戏（MAX and MIN,MAX先走）可如下形式化描述，从而将其转换为对抗搜索问题。
下面我们通过Tic-Tac-Toe游戏来理解一下对抗搜索。
游戏规则：
- MAX先行，可在初始状态的9个空格中任意放一个X
- MAX希望游戏终局得分高、MIX希望游戏终局得分低
- 所形成游戏树的叶子结点有9！=362880，国际象棋的叶子节点数为10^40
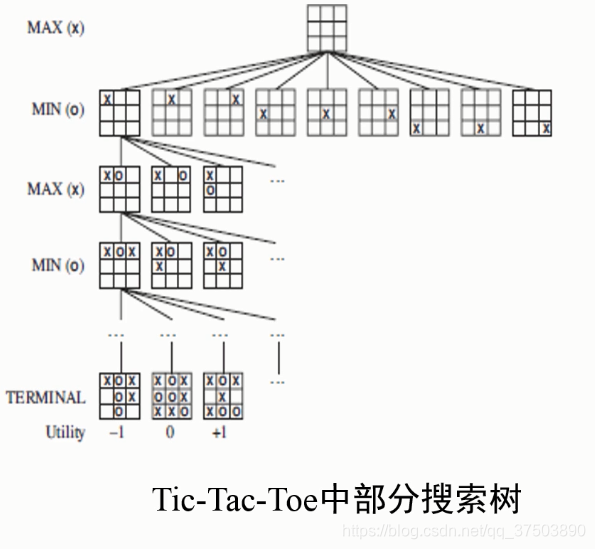
我们的目标是，选择一个最优策略保证MAX选手的利益最大化。
1、
最低0.47元/天 解锁文章
扫一扫
4130
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
